Jak działa CRC?

Rozdział 4 Arytmetyka CRC

Rozdz. 4.1 Wstęp
Zaczniemy tematu, który znasz już ze szkoły podstawowej a jest nim dzielenie pisemne. Potem przekonasz się, że obliczanie CRC jest podobne, tylko  dużo prostsze. Nie musisz się zastanawiać ile razy “coś” się mieści w “czymś”. Nie ma też nic “w pamięci”. Tylko xor-ujesz i przesuwasz!
Rozdz. 4.2 Przykład dzielenia dziesiętnego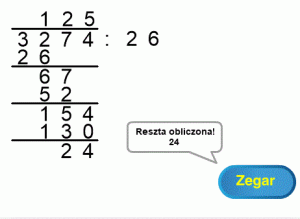

Rys. 4-1
Przykład dziesiętnego dzielenia pisemnego    ANIMACJA
Przypomnij sobie dzielenie  sobie klikając ANIMACJ-ę.

Rozdz. 4.3 Ćwiczenia z xor-owania
Zanim przejdziemy do obliczania CRC to musisz być dobry w xor-owaniu wyrażeń będących wierszami.

Rys. 4-2
Pod kreską każdego xor-owania jest wiersz, którego element jest xor-em elementów w kolumnie nad nim. Sprawdź to dla Rys. 4-2a i 4-2b.
Przy większej ilości wierszy jak na Rys. 4-2c wynikiem jest 0 gdy jest parzysta liczba jedynek w kolumnie i 1 gdy nieparzysta.

Rozdz. 4.4 Przykład obliczania CRC
Jest to jeden z najważniejszych punktów w tym kursie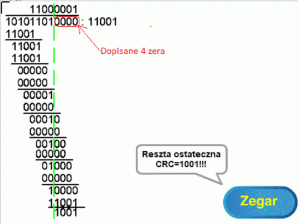

Rys. 4-3
Przykład obliczania CRC jako “reszty” z “dzielenia” ANIMACJA
To działanie tylko przypomina dzielenie, dlatego użyłem cudzysłowów.
“Dzielimy” “dzielną” 10101101 przez “dzielnik” 11001.  Otrzymany nad kreską “iloraz” 11000001 nie interesuje nas. Ważna jest tylko reszta z “dzielenia” 1001.
Porównaj z dzieleniem pisemnym z Rozdz. 4.2 i spróbuj samemu ustalić algorytm.
Powinien być następujący.
1. Dopisz 4 zera bo dzielna ma 5 cyfr
2. Napisz pierwsze 1 na 5 pozycji nad górną kreską bo dzielnik 11001 ma 5 cyfr
3. Oblicz pierwszą “resztę” jak w zwykłym dzieleniu dziesiętnym. Czyli od 10101 “odejmujemy” 1×11001=11001. “Odejmowanie” zastępujemy xor-owaniem. Pierwszą resztą jest 1100.
4. Dopisz 1 do “ilorazu” nad górną kreską bo pierwsza reszta była niezerowa. Gdyby była zerowa to dopisałbyś 0.
Oblicz drugą resztę. Jest nią 0000.
…
itd
Obliczanie kończymy gdy kolejna “reszta” znajdzie się dokładnie pod dopisanymi 4  “zerami”.  Ostateczną “resztą” będzie 1001.
Spróbuj teraz samemu obliczyć resztę  na kartce papiery. Tzn oblicz resztę z “dzielenia” 10101101:11001.
Otrzymanym wynikiem jest właśnie CRC=1001 z wysłanej wiadomości gdy “dzielnikiem” jest 11001.

Rozdz. 4.5 Modyfikacja obliczania CRC
A gdyby tak na początku zamiast 0000 dopisać 1001 jako resztę z dzielenia z poprzedniego przykładu ? To Jakie teraz otrzymamy CRC?
Chyba słyszę odpowiedź, że CRC=0000. Brawo, wygrał Pan telewizor! No to sprawdźmy.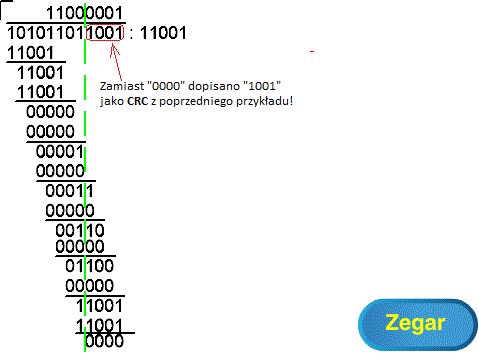

Rys. 4-4
Jaka jest “reszta” gdy zamiast “0000” dopiszemy “1001” jako “resztę” z poprzedniego przykładu?  ANIMACJA
“Dzielimy” “dzielną” 10101101 przez “dzielnik” 11001.  Zauważ, że do czwartej reszty przebieg “dzielenia” jest identyczny jak poprzednio. Jest to oczywiste, ponieważ dopisane 1001 nie wpływa jeszcze na działania. Tak jak przypuszczaliśmy ostatecznie CRC=0000.
W następnym rozdziale okaże się, że ten  algorytm też jest używany w transmisji danych. Dla niektórych jest nawet bardziej elegancki!