Podstawy automatyki
Rozdz. 19. Kryterium stabilności Nyquista
Rozdz. 19.1 Wstęp
Układ otwarty jest z reguły stabilny. Może stać się niestabilnym dopiero po zamknięciu go pętlą sprzężenia zwrotnego. Kryterium Nyquista potrafi przewidzieć na podstawie charakterystyki amplitudowo – fazowej układu otwartego ( który jest „łatwiejszy” niż zamknięty) stabilność układu zamkniętego. Układ otwarty jest po pierwsze prostszy od zamkniętego, a po drugie jest przeważnie stabilny. Mam na myśli układ otwarty, że tak powiem ” z natury”, a nie taki który po zastosowaniu wzoru na Gz(s) staje się „otwarty” tak jak poniżej.
Rys. 19-1
Kryterium Nyquista należy do częstotliwościowych, w przeciwieństwie do algebraicznego kryterium Hurwitza z następnego rozdziału.
Charakterystykę częstotliwościową układu otwartego wyznacza się stosunkowo łatwo. Możesz to zrobić „na żywca” na obiekcie bez obaw, że stracisz panowanie nad instalacją przemysłową. Jest to przecież układ otwarty, a więc stabilny. I to jest właśnie zaletą kryterium Nyquista.
Rozdz. 19.2 Kryterium Nyquista
W rozdz. 18 poznaliśmy charakterystyki amplitudowo-fazowe. Są podstawą do zrozumienia Kryterium Nyquista .
Zbadamy 3 otwarte układy dynamiczne, które na Rys.19-2 mają żółtą, zieloną i czerwoną charakterystykę amplitudowo-fazową. Odpowiadają one trzem kolejnym członom trójinercyjnym z Rozdz. 19.4, 19.5 i 19.6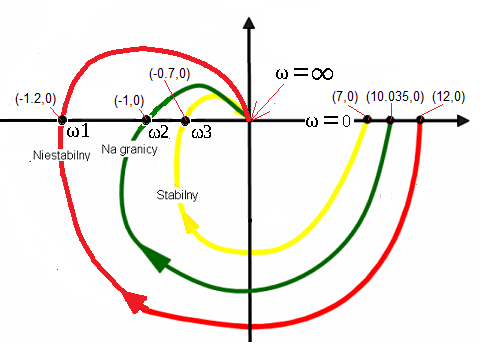
Rys. 19-2
Wszystkie 3 charakterystyki dotyczą układów otwartych.
Napisy Stabilny, Na granicy i Niestabilny dotyczą stanu, ale dopiero po zamknięciu ich pętlą ujemnego sprzężenia zwrotnego!
Na wykresie nie jest zachowana skala. Punkty na osi x tj. (7,0), (10.035,0) i (12,0) to liczniki tych transmitancji, inaczej wzmocnienia K w stanie ustalonym. Z nich „startują” poszczególne charakterystyki z początkową pulsacją ω=0. W pulsacjach ω1,ω2 i ω3 charakterystyki przechodzą przez oś x w punktach x (-1.2,0), (-1,0) i (-0.7,0). Sinusoidy mają tu przesunięcie fazowe φ=-180°. Ponieważ są to człony trójinercyjne, to przechodzą one przez 3 ćwiartki i dla ω=∞ kończą w punkcie (0,0).
A teraz najważniejsze, czyli Kryterium Nyquista!
1. Jeżeli charakterystyka nie obejmuje punktu (-1,0), to układ zamknięty będzie stabilny–>charakterystyka żółta .
2. Jeżeli charakterystyka przechodzi przez punkt (-1,0), to układ zamknięty będzie na granicy stabilności–>charakterystyka zielona.
3. Jeżeli charakterystyka obejmuje punkt (-1,0), to układ zamknięty będzie niestabilny–>charakterystyka czerwona.
Rozdz. 19.3 Sprawdzenie Kryterium Nyquista dla układu stabilnego, na granicy i niestabilnego.
Konkretnymi przykładami będą 3 człony trójinercyjne odpowiadające charakterystyce żółtej, zielonej, czerwonej z Rys.19-2. Różnić je będzie tylko licznik transmitancji G(s), czyli wzmocnienie K=7, 10.035 i 12. Najpierw wyznaczymy w sposób maksymalnie uproszczony charakterystykę amplitudowo-fazowe danej transmitancji G(s)-czyli żółtej, zielonej, czerwonej, w układzie otwartym. Potem zamkniemy je pętlą ujemnego sprzężenia zwrotnego i impulsem Diraca będziemy wytrącać układy ze stanu równowagi.
Rozdz. 19.4 Sprawdzenie Kryterium Nyquista dla transmitancji “K=7”.
Czyli stabilnej –żółtej.
Rozdz. 19.4.1 Charakterystyka amplitudowo-fazowa układu otwartego
Wyznaczymy charakterystykę amplitudowo-fazową dla wszystkich pulsacji w zakresie ω=0…∞ podając na wejście sinusoidy x(t)=1sin(ωt) o różnych częstotliwościach. W praktyce wystarczy dla skończonej liczby pulsacji ω. Podobnie badaliśmy np. człon inercyjny w Rozdz. 18. Problem uprościmy jeszcze bardziej. Ograniczymy się tylko do pulsacji ω3, w której charakterystyka przetnie oś x w punkcie (-0.7,0). Pozostałe 2 punkty tj:
(7,0) dla ω=0
(0,0) dla ω=∞
wynikają z Rys. 19-2 i są oczywiste.
Rys. 19-3
Dla pulsacji ω3=2/sek (odpowiadająca okresowi T=3.14sek) sinusoida wyjściowa y(t) w stanie ustalonym jest przesunięta w fazie względem x(t) o φ=-180°. Pulsację ω3 znalazłem metodą prób i błędów. Sygnał wyjściowy y(t) jako sinusoida ustalił się po ok. 20 sek. Dopiero wtedy można mierzyć jej parametry tj. amplitudę, okres i fazę. Sinusoida wejściowa x(t) ma amplitudę 1. Dlatego amplituda y(t)=0.7 jest też wzmocnieniem dla ω3. Czyli K(ω3)=-0.7. Znak minus wynika z fazy φ=-180°. Oznacza to, że żółta charakterystyka przecina oś x dla ω3 w punkcie (-0.7,0). Nie obejmuje więc punktu (-1,0) i tak jest na Rys. 19-2.
Wniosek
Układ zamknięty powinien być stabilny.
Rozdz. 19.4.2 Czy układ zamknięty będzie stabilny?
Rys. 19-4
Człon trójinercyjny z K=7 w układzie zamkniętym. Wejściem x(t) jest impuls Diraca
Impuls Diraca wytrącił układ ze stanu równowagi, ale po kilku oscylacjach ω=1.76/sek system znowu wrócił do stanu y(t)=0. Czyli system jest stabilny. „Żólta” charakterystyka na Rys. 19-2 nie obejmuje punktu x=(-1,0). Potwierdza to tezę nr 1 Kryterium Nyquista.
Uwaga:
Początkowo x(t)=dirac a potem x(t)=0. Dlatego prawie cały czas e(t)=0-y(t), czyli e(t)=-y(t).
Rozdz. 19.5 Sprawdzenie Kryterium Nyquista dla transmitancji “K=10.035”.
Czyli na granicy-zielonej.
Rozdz. 19.5.1 Charakterystyka amplitudowo-fazowa układu otwartego
Ograniczymy się do do pulsacji ω2, w której zielona charakterystyka przecina oś x w punkcie (-1,0). Zauważ, ze ω2=ω3=2/sek. Jest to oczywiste, bo wszystkie 3 transmitancje te różnią się tylko wzmocnieniem K w liczniku. Czyli dla następnej transmitancji “K=12” też jest ω1=2/sek.
Rys. 19-5
Dla ω2≈2/sek sinusoida wyjściowa w stanie ustalonym y(t)=1 jest przesunięta w fazie o φ=-180° i jej amplituda jest równa wejściowej x(t). Czyli K(ω2)=-1. Mamy więc wyznaczone 3 ważne punkty zielonej charakterystyki dla ω=0, ω=ω2=2/sek i ω=∞ tak jak na Rys. 19-2.
Wniosek
Układ zamknięty powinien być na granicy stabilności.
Sprawdźmy.
Rozdz. 19.5.2 Czy układ zamknięty będzie na granicy stabilności?
Rys. 19-6
Człon trójinercyjny z K=10.035 w układzie zamkniętym.
Wejście x(t)=Impuls Diraca wytrąciło układ ze stanu równowagi i powstały drgania o stałej amplitudzie i pulsacji ω=2/sek. Czyli układ jest na granicy stabilności. Zielona charakterystyka układu otwartego z Rys. 19-2 przecina punkt (-1,0). Potwierdza to tezę nr 2 Kryterium Nyquista.
Rozdz. 19.6 „Czerwony” który w układzie zamkniętym powinien być niestabilny.
Czyli niestabilnej-czerwonej.
Rozdz. 19.6.1 Charakterystyka amplitudowo-fazowa układu otwartego
Ograniczymy się do do pulsacji ω1, w której charakterystyka przetnie oś x w punkcie x=-1.2 Pozostałe 2 punkty dla ω=0 i ω=∞ są oczywiste.
Rys. 19-7
”Dla pulsacji ω1=2/sek sinusoida wyjściowa w stanie ustalonym y(t) jest przesunięta w fazie o φ=-180° i jej amplituda to 1.2. Czyli K(ω1)=-1.2. Mamy więc wyznaczone 3 ważne punkty czerwonej charakterystyki dla ω=0, ω=ω1=2/sek i ω=∞ z Rys. 19-2.
Oznacza to, że czerwona charakterystyka przecina dla ω1 w punkcie (-1.2,0) oś x. Czyli obejmuje punkt (-1,0). I tak jest na Rys. 19-2.
Wniosek
Układ zamknięty powinien być niestabilny.
Sprawdźmy.
Rozdz. 19.6.2 Czy układ zamknięty będzie niestabilny?
Rys.19-8
Człon trójinercyjny z K=12 w układzie zamkniętym.
Wejście x(t)=Impuls Diraca wytrąciło układ ze stanu równowagi i powstały drgania o rosnącej amplitudzie i pulsacji ω=2.14/sek. Czyli układ jest niestabilny. Czerwona charakterystyka układu otwartego z 19-2 obejmuje punkt (-1,0). Potwierdza to tezę nr 3 Kryterium Nyquista.
Rozdz. 19.7 Nyquist intuicyjnie
Rozdz. 19.7.1 Wstęp
Nie wiem czy się uda, ale spróbuję. Otóż w kryterium Nyquista pojawia się bardzo charakterystyczny punkt (-1,0). Stabilność układu zamkniętego zależy od tego, jak przebiega charakterystyka amplitudowo-fazowa układu otwartego względem tego punktu.
Wróć na chwilę do Rozdz. 17 Niestabilność, czyli Jak Powstają Drgania p.17.2.
Tu było coś podobnego:
Gdy wzmocnienie:
K<1 to układ zamknięty jest stabilny
K=1 to układ zamknięty jest „na granicy”
K>1 to układ zamknięty jest niestabilny
Trochę naciągając rzeczywistość stwierdziłem, że odpowiedzi na Diraca członu opóźniającego i trójinercyjnego są podobne, tylko w tym ostatnim odpowiedź jest bardziej „rozmyta”. Tu znowu wyszedł chyląc kapelusza jakiś uproszczony Nyquist.
Spróbuję więc wyjaśnić jak działa prawdziwe już Kryterium Nyquista dla 3 wcześniej badanych członów trójinercyjnych:
–„Żółtego”
–„Zielonego”
–„Czerwonego”.
Rozdz. 19.7.2 Dlaczego „Żółty” to stabilny?
Dlaczego żółta charakterystyka układu otwartego z Rys. 19-2 nieobejmująca punktu (-1,0) oznacza stabilność układu zamkniętego?
Układ otwarty dla pulsacji ω3=2/s wg. Rys. 19-3 ma wzmocnienie K=-0.7. Znak minus to przesunięcie fazowe.
Spójrz teraz na Rys. 19-4 gdzie zastosowano ujemne sprzężenie zwrotne.
Na wejście trójinercyjnego wchodzi y(t) z odwróconą fazą, bo po 3 sekundzie cały czas jest x(t)=0 i e(t)=x(t)-y(t)=-y(t)
Z kolei wiemy, że dla tej częstotliwości w stanie ustalonym ω=1.76*1/s–>Rys. 19-4, człon trójinercyjny prawie odwraca fazę. Prawie bo wg. Rys. 19-3 odwraca fazę dla ω3=2*1/sek
Faza jest więc 2 razy odwrócona, czyli w stanie ustalonym sinusoida y(t) jest w fazie z sygnałem na wejściu! Powstało coś podobnego do dodatniego sprzężenia zwrotnego o wzmocnieniu K=+0.7 na Rys.17-5 rozdz. 17! Ponieważ K=+0.7<1 to sygnał sam się nie podtrzyma (tak jak w dodatnim sprzężeniu zwrotnym) i drgania zanikną. Układ zamknięty będzie stabilny.
Rozdz. 19.7.3 Dlaczego „zielony” jest na granicy stabilności?
Dla Żółtego uklad otwarty dla ω3=2*1/s miał K=-0.7. Analogicznie dla Zielonego uklad otwarty dla ω2=2*1/s miał K=-1 (Rys. 19-5).
Rozumując podobnie jak dla „Żółtego” dojdziemy do wniosku, że „pseudododatnie” sprzężenie zwrotne” o wzmocnieniu K=+1 wywoła drgania o stałej amplitudzie podobnie jak na Rys.17-7 rozdz. 17. Drgania same się podtrzymają i układ zamknięty będzie na granicy stabilności.
Rozdz. 19.7.4 Dlaczego „czerwony” jest niestabilny
Wzmocnienie układu otwartego K=-1.2 (Rys. 19-7). Dlatego ”pseudododatnie” sprzężenie zwrotne” o wzmocnieniu K=+1.2>1 spowoduje drgania o narastającej amplitudzie podobnie jak na Rys.17-9 rozdz. 17. Układ zamknięty będzie niestabilny.
Rozdz. 19.8 Wyznaczanie charakterystyki amplitudowo-fazowej na podstawie znanej transmitancji G(s)
W rozdz. 19.3 wyznaczaliśmy charakterystyki członów G(s) metodą doświadczalną podając na wejście sinusoidę x(t) o amplitudzie 1 i mierząc amplitudę oraz fazę sinusoidy wyjściowej y(t). Robiliśmy to dla różnych pulsacji ω, teoretycznie w przedziale 0…∞. Nie była potrzebna żadna wiedza o liczbach zespolonych . Wystarczyła interpretacja sinusoidy jako wektora o odpowiedniej długości i kącie na płaszczyźnie x,y.
Od wektorów do liczb zespolonych jest bardzo blisko. Tak jak wektor ma współrzędne płaszczyźnie x,y, tak liczba zespolona ma współrzędne płaszczyźnie P, Q gdzie P jest osią składowej rzeczywistej a Q składowej urojonej. Na liczbach zespolonych też się wykonuje operacje znane w „zwykłej” matematyce. Dodawanie, odejmowanie, mnożenie i dzielenie. Są na to odpowiednie wzory i już. Tak że znając je, można wyznaczyć charakterystykę amplitudową-fazową danego G(s). Należy pod s podstawić liczbę urojoną jω, gdzie ω to odpowiednia pulsacja i liczba zespolona G(jω) pokaże nam odpowiednią wartość dla pulsacji ω.
Przypominam, że G(s) jest ułamkiem dwóch wielomianów licznika L(s) i mianownika M(s). Do tego jest nam tylko potrzebna małpia zręczność wykonywania 4 podstawowych operacji matematycznych na liczbach zespolonych. Obliczona w ten sposób charakterystyka amplitudowo-fazową dla różnych pulsacji ω będzie wyglądała podobnie jak dotychczas: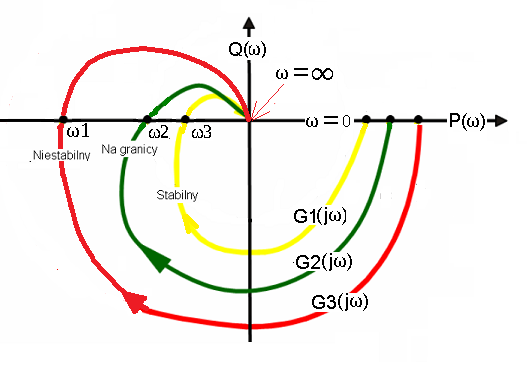
Rys.19-9
Charakterystyka amplitudowo-fazowa G(jω) obliczona z transmitancji G(s).
G(jω) to tzw. transmitancja widmowa. Zawiera w sobie taką samą informacje o właściwościach statycznych i dynamicznych obiektu jak transmitancja operatorowa G(s).
Uwaga:
Wszystkie pulsacje ω1,ω2 i ω3 na Rys.19-2 były jednakowe tzn. ω1=ω2=ω3=2/sek. Ale tylko dlatego, że mianowniki transmitancji G1(s), G2(s) i G3(s), są takie same! Przeważnie tak nie jest i dlatego zwykle ω1,ω2 i ω3 są różne.
