Jak działa CRC?
Rozdział 3 Funkcje Logiczne
Rozdz. 3.1 Wstęp
Wspominałem już, że CRC jest traktowane jako swego rodzaju “reszta” z dzielenia. “Dzielną” jest wysyłana wiadomość, “dzielnikiem” pewna stała znana Nadajnikowi i Odbiornikowi a “resztą” właśnie to CRC. Zaraz, zaraz a to co najważniejsze czyli wynik dzielenia-“iloraz”? To nas zupełnie nie interesuje! Stop-więcej na ten temat w Rozdz. 4 Arytmetyka CRC. Na razie powiem tylko tyle, że zamiast dzielenia będziemy stosować coś co jest tylko podobne do dzielenia. W tym, że dla “dzielnej” i “dzielnika” też jest “reszta” która wymaga mniej bajtów niż “dzielna”. I najważniejsze. Zamiast kolejnych odejmowań wykonujemy bardzo prostą operację logiczną xor-owanie. W dodatku nie ma “nic w pamięci” jak w pisemnym dzieleniu dziesiętnym. Operacje te są tak proste i szybkie, że idealnie nadają się do obliczania CRC. Wykonywane są w czasie wysyłania kolejnego bitu i nie spowalniają transmisji. Dlatego w dalszych rozdziałach musisz być bardzo dobry w xor-owaniu.
Ale najpierw poznasz podstawowe funkcje logiczne:
– NEGACJA czyli zaprzeczenie
– AND czyli iloczyn logiczny
– OR czyli suma logiczna
oraz oczywiście
– XOR czyli albo
Rozdz. 3.2 Funkcja Logiczna NEGACJA inaczej Zaprzeczenie
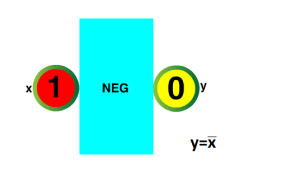
Rys. 3-1
Funkcja Negator po naszemu “NIE” ANIMACJA
Wyjście y jest negacją wejścia x co zapisujemy tak jak na rysunku (y=x z “daszkiem”). Wejdź w animację i napisz tabliczkę prawdy.
Jak nie wiesz o co chodzi, to rzuć okiem na Rys 3-5a w Rozdz. 3.6
Rozdz. 3.3 Funkcja Logiczna OR inaczej Suma Logiczna
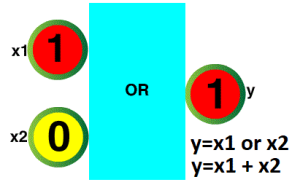
Rys. 3-2
Funkcja OR po naszemu “LUB” ANIMACJA
Funkcję można zapisać tak y=x1 or x2 lub jak zwykłą sumę y=x1+x2
y=1 tylko wtedy gdy x1=1 lub x2=1
Wejdź w animację, sprawdź powyższe zdanie i napisz tabliczkę prawdy.
Rozdz. 3.4 Funkcja Logiczna AND inaczej Iloczyn Logiczny
Rys. 3-3
Funkcja AND po naszemu “I” ANIMACJA
Funkcję można zapisać tak y=x1 and x2 lub jak zwykły iloczyn y=x1*x2
Y=1 tylko wtedy gdy x1=1 i x2=1 jednocześnie
Wejdź w animację, sprawdź powyższe zdanie i napisz tabliczkę prawdy.
Rozdz. 3.5 Funkcja Logiczna XOR
Rys. 3-4
Funkcja XOR po naszemu “ALBO” ANIMACJA
Y=1 tylko wtedy gdy x1=1 albo x2=1
Wejdź w animację, sprawdź powyższe zdanie i napisz tabliczkę prawdy.
Przy okazji. Niektórzy nie rozróżniają spójnika “ALBO” od “LUB”.
Nasze prawo pozwala na małżeństwo “z Jolą albo z Mariolą” ale nie “z Jolą lub z Mariolą”. To ostatnie dopuszczałoby bigamię!
Rozdz. 3.6 Funkcje Logiczne w postaci tabelek prawdy (tabelek Karnaugh)
|Rys. 3-5
Tabelki prawdy
Bardzo wygodne jest przedstawianie danej funkcji logicznej w postaci tzw. tabelki prawdy. Szczególnie wtedy, gdy badamy jakieś urządzenie i nie znamy jeszcze jego funkcji logicznej. Rys. 3-5a…3-5d to wyniki badań układów logicznych z Rozdz. 3.2…3.5. Każda komórka tabelki prawdy odpowiada jednej badanej kombinacji wejść. Np. na Rys. 3-5b dotyczącego funkcji OR zaznaczone kółkiem 1 oznacza, że dla kombinacji wejść x1=1 i x2=0 wyjście y=1. Funkcja ta ma 2 wejścia x1 i x2 dla których są 4 różne kombinacje wejść x1 i x2 . Dlatego jej tabelka prawdy to kwadrat o wymiarach 2×2. Uwaga ta dotyczy wszystkich badanych układów z 2 wejściami. Symbol OR można zastąpić “+”, zaś AND symbolem mnożenia “*”. Są chyba nawet bardziej popularne.
Rys. 3-5a
Negator
Dla wejścia x=0 wyjście y=1 i dla wejścia x=1 wyjście y=0. Jest to wynik badania negatora z Rys. 3-1.
Rys. 3-5b
OR
Rys. 3-5c
AND
Rys. 3-5d
czyli funkcja XOR dobrze ilustruje fakt, że każde 1 to osobny iloczyn logiczny z x1 i x2. Tu niektóre x1 x2 w iloczynie są “zadaszkowane” czyli zanegowane.
Teraz może rodzić się pytanie. O ile jest to oczywiste dla funkcji AND i XOR to już funkcja OR powinna składać się z 3 odpowiednio zadaszkowanych iloczynów! A tu jest tylko proste y=x1+x2! Okazuje się, że każdą funkcję logiczną podaną w postaci tabelki można próbować uprościć! W latach 50 niejaki Karnaugh pokazał jak to robić w pewnym ograniczonym przypadku. Mianowicie dla funkcji z maksimum 5 wejściami x1 x2 x3 x4 x5 użył tzw. sklejania. A to nic innego jak prawa logicznego którego używamy na co dzień. O jej szczegółach nie będę mówił mówił więcej oprócz poniższego.
Można powiedzieć “Jutro będzie świeciło słońce i będzie padał deszcz lub jutro będzie świeciło słońce i nie będzie padał deszcz”. Mam nadzieję że widzisz tu sumę 2 iloczynów logicznych! To samo można powiedzieć znacznie prościej “Jutro będzie świeciło słońce”. To absolutnie ta sama treść! Dlatego papugi na wydziałach prawa uczą się logiki matematycznej. Potem broniąc klienta przed sądem wyrażają się krótko i zwięźle.
Rys. 3-5e
to przykład funkcji z 3 wejściami x1 x2 x3. Każda komórka to inna kombinacja tych wejść odpowiadająca innemu iloczynowi. Spróbuj samemu rozpracować iloczyn z kółkiem a zwłaszcza daszki-negacje z odpowiednimi zerami x2 x3 a także kombinacje dla pozostałych 4 komórek tabeli z 1. Dla tej funkcji z 3 wejściami mamy tabelkę o wymiarach 2×4. Analogicznie dla funkcji 4-wejściowych jest tabelka 4×4 a dla 5-wejściowych tabelka 4×8. Wracając zaś do Rys. 3-5e to tę samą funkcję da się przedstawić w postaci, że tak powiem “surowej”. Inaczej kanonicznej czyli w postaci 5 iloczynów o 3 składnikach każdy. Dzięki panu Karnaugh, używając tzw. sklejania, można ją też przedstawić w postaci 2 tylko iloczynów. W dodatku krótszych, bo pierwszy ma tylko 2 składniki a drugi 1. Dlatego układ elektroniczny realizujący tę funkcję będzie prostszy, tańszy i bardziej niezawodny.
Więcej o metodzie Karnaugh znajdziesz w internecie.
