Jak działa CRC?
Rozdział 7 A gdyby tak przesuwać o 2 bity?
Rozdz. 7.1 Wstęp
Z poprzedniego rozdziału wiemy, że rzeczywisty rejestr CRC ma 1, 2, lub 4 bajty długości. A czym się jeszcze różni od tego z rozdz. 5? Przede wszystkim przesunięciami. We wcześniejszych rozdziałach były bitowe, a te których się powszechnie używa są bajtowe. Przeważnie jest tak, że program chcąc wysłać np. 100 bajtów, wprowadza je bajt po bajcie do tzw. UART-u, a ten samodzielnie wysyła je bit po bicie w sieć. A jak to robi, to już zadanie układu typu UART, zaprojektowanego przez jakiegoś kolesia kilkadziesiąt lat temu. Czyli program wysyłając 1 bajt musi także obliczyć stan CRC po 8 przesunięciach bitowych! Pierwsze co nam przychodzi do głowy, to program który wykonana 8 jednobitowych przesunięć wg. Rozdz. 5.2. Jest to raczej nie stosowana w praktyce, czasochłonna i opóźniająca transmisję metoda SIMPLE. Wady tej nie mają powszechnie stosowane tzw. metody tablicowe. Niestety duże wymiary tych tablic 256×8 a nawet 256×32, utrudniają zrozumienie zasady działania. Dlatego najpierw poznamy metody CRC dla przesunięć 2-bitowych. Tablice mają tu małe rozmiary 4×8 i są łatwiejsze do analizy. Potem już bez problemu ogarniesz w Rozdz. 8 “prawdziwe” tablicowe metody CRC.
Rozdz. 7.2 Jednobajtowy Układ Obliczania CRC z przesunięciem 1-bitowym
Rys. 7-1
Jednobajtowy Układ Obliczania CRC z przesunięciem bitowym ANIMACJA
Jest to już bardziej zbliżona do rzeczywistości wersja układu z Rozdz. 5.2. Zamiast 4-bitowego CRC mamy 8-bitowe i zamiast 1 bajtu przesyłanej informacji (inaczej “dzielnej“) w rejestrze A są 2 bajty. W rzeczywistych systemach działających w sieci (a nie tylko w tym kursie) w rejestrze A tych bajtów może być tysiące, a nie tylko 2! “Dzielnikiem” jest 1 10010101 z czego 8 młodszych bitów jest jak zwykle umieszczona pod adresem 1 w tablicy o wymiarach 2×8. Widzimy, że poznana dotychczas metoda obliczania CRC też jest tablicowa! I to z całkiem poważną tablicą 2×8!
Kliknij animację i zobacz jak jest obliczane CRC dotychczasową metodą bit po bicie, czyli SIMPLE. Następne przykłady w tym rozdziale będą jego modyfikacją z 2-bitowym przesunięciem i 8-bitowym przesunięciem w Rozdz. 8. W tym rozdziale “Dzielna” czyli przesyłana informacja oraz “Dzielnik” będą we wszystkich animacjach takie same. Czyli wynikiem końcowym powinno być zawsze CRC=11100110.
Jednak w Rozdz. 7.6 jest inne CRC i nie wiem dlaczego! Tu liczę na pomoc czytelników.
Rozdz. 7.3 Jakie jest CRC po przesunięciu 2-bitowym?
Rozdz. 7.3.1 Wstęp
Wiemy już jaki będzie stan CRC po przesunięciu 1-bitowym. Możemy więc też przewidzieć stan po następnym przesunięciu 1-bitowym, czyli w sumie po 2 przesunięciach bitowych. Dlatego zbadamy CRC po przesunięciu 2-bitowym dla wszystkich możliwych kombinacji 2 bitów początkowych rejestrów CRC tj. 00, 01, 10 i 11.
Rozdz. 7.3.2 CRC z przesunięciem 2-bitowym gdy 2 pierwsze bity to 00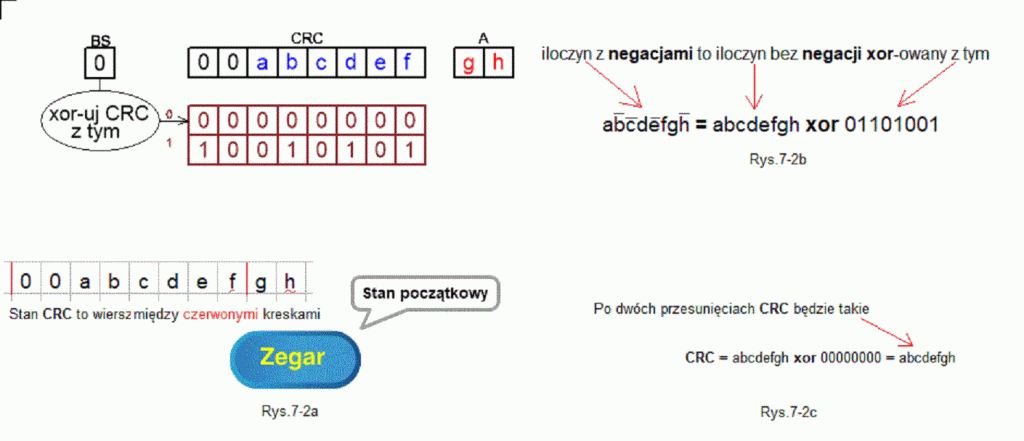
Rys. 7-2
Stan początkowy gdy 2 pierwszymi bitami CRC jest 00 ANIMACJA
Akurat w tym przypadku sprawa jest banalna. Bity abcdefgh będą tylko przesunięte, ponieważ po każdym przesunięciu BS=0.
To oznacza, że CRC będzie xor-owane z wartością zerową a ta operacja nic nie zmienia.
Rys. 7-2a przedstawia stan początkowy CRC jako bity między czerwonymi kreskami. Z animacji wynika, że operacjom na rejestrach towarzyszą odpowiednie xor-owania z zerowymi wierszami, których wynik jest xor-em wszystkich wierszy między czerwonymi kreskami .
Rys. 7-2b pokazuje zasadę że każdy iloczyn logiczny z negacjami można przedstawić jako iloczyn bez negacji xor-owany z odpowiednią liczbą bitową. Liczba ta ma bit=1 na tej pozycji na której iloczyn ma wartość zanegowaną (“zadaszkowaną”). Zapamiętaj tą zasadę!
Rys. 7-2c pokazuje stan CRC po 2 przesunięciach jako CRC=abcdefgh xor 00000000.
Rozdz. 7.3.3 CRC z przesunięciem 2-bitowym gdy 2 pierwsze bity to 01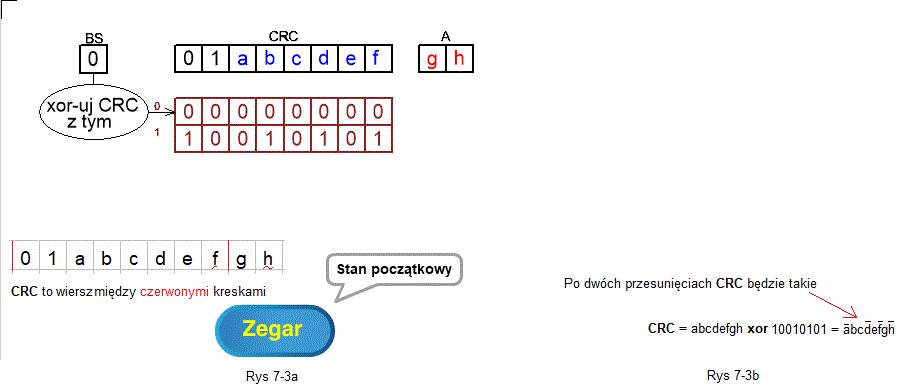
Rys. 7-3
Stan początkowy gdy 2 pierwszymi bitami CRC jest 01 ANIMACJA
W Rozdz. 7.3.2 przewidzenie stanu CRC było banalne bo były tylko same przesunięcia.
Teraz stanem początkowym jest CRC=01abcdef. Bity gh czekają w pamięci A. Pozostałe bity pamięci A z oczywistych powodów nas nie interesują. Przecież nie będą miały wpływu na stan CRC po 2 przesunięciach.
Teraz pojawi się stan BS=1 i nie będzie tak miło. Stan po 2 przesunięciach przewidzisz 2 metodami:
1. Używając animacji. A ponieważ znasz zasady to jesteś w stanie zrobić to “w głowie”.
2. Metodą rachunkową czyli też “w głowie”. Sam ją rozpracuj korzystając z animacji. Jeżeli się nie uda to metoda jest następująca:
– Napisz 01abcdefgh. Stan początkowy rejestru CRC, czyli 01abcdef oddziel czerwonymi kreskami jak na Rys. 7-3a. Następne BS=0 bo pierwszym bitem CRC jest 0
– Napisz nad stanem początkowym przesunięte 00000000 bo BS=0. Teraz nowym stanem CRC jest xor 2 wierszy między czerwonymi kreskami. Na razie nie musisz tego obliczać ale sprawdź dla własnej satysfakcji czy jest jak w animacji. Następne BS=1 jako xor pierwszej kolumny między czerwonej kreskami
– Napisz przesunięte 10010101 bo BS=1. Nowym i ostatecznym stanem CRC jest xor 3 wierszy między czerwonymi kreskami czyli CRC=abcdefgh xor 10010101 jak na Rys. 7-3b
Po 2 przesunięciach CRC=abcdefgh xor 10010101.
Uwagi:
– We wzorze na CRC wartość 10010101 za symbolem xor jest xor-em 2 wierszy nad abcdefgh po drugim przesunięciu
– Po drugim przesunięciu nad symbolami a, d, f i h pojawiły się “daszki” –>Rys. 7-3b, co oznacza, że te wartości zostały zanegowane.
Rozdz. 7.3.4 CRC z przesunięciem 2-bitowym gdy 2 pierwsze bity to 10
Rys. 7-4
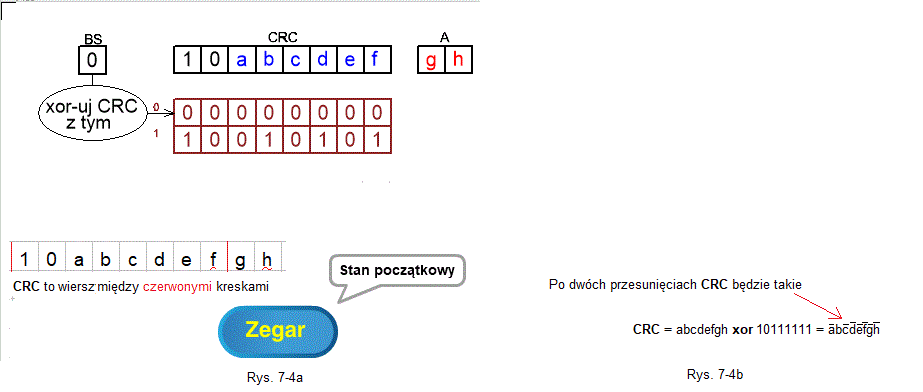
Stan początkowy gdy 2 pierwszymi bitami CRC jest 10 ANIMACJA
Po 2 przesunięciach CRC=abcdefgh xor 10111111.
Rozdz. 7.3.5 CRC z przesunięciem 2-bitowym gdy 2 pierwsze bity to 11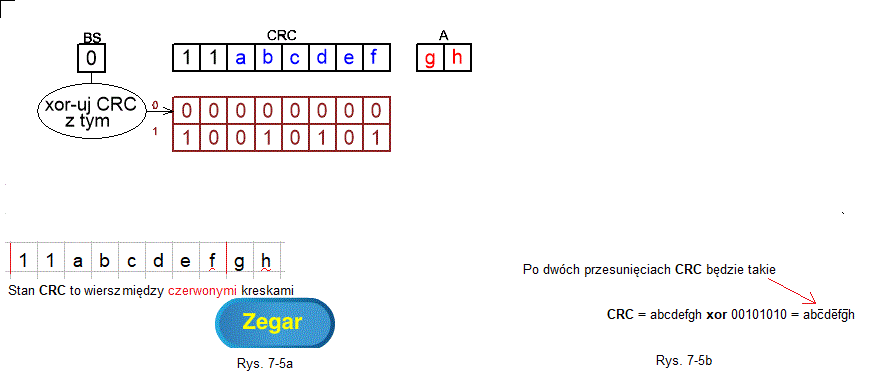
Rys. 7-5
Stan początkowy gdy 2 pierwszymi bitami CRC jest 11 ANIMACJA
Po 2 przesunięciach CRC=abcdefgh xor 00101010.
Rozdz. 7.3.6 Tablica jako podsumowanie tego rozdziału
Z powyższych podrozdziałów wynika, że znając 2 bity początkowe CRC możemy od razu obliczyć jego nowy stan po przesunięciach stosując odpowiednie xor-owanie.
Gdy 2 pierwsze bity:
– 00 to następne CRC=CRC xor 00000000
– 01 to następne CRC=CRC xor 10010101
– 10 to następne CRC=CRC xor 10111111
– 11 to następne CRC=CRC xor 00101010
Odpowiada to tablicy 4×8 o 4 adresach 00, 01, 10 i 11 na Rys. 7-6. Aktualny stan 2-bitowego rejestru BS wskazuje przez jaki wiersz należy xor-ować CRC aby trzymać nowy stan po przesunięciu 2-bitowym. Jest tu pewna analogia do Rys. 7-1 z przesunięciem 1-bitowym i tablicą 2 wierszową.
Rozdz. 7.4 Metoda tablicowa bezpośrednia dla przesunięć 2-bitowych
Najpierw o nazwie którą zaproponowałem. Tablicowa-bo używa tablic, zresztą tak jak z metoda przesunięciem 1-bitowym np. z Rys. 7-1. A bezpośrednia? Bo oparta jest na arytmetyce z Rozdz. 4.4 z dodaniem zer i jej rejestrowej realizacji na Rys. 7-1. Innym uzasadnieniem może też być pojedyncze xor-owanie, a nie podwójne jak w rozdz. 7.5 i 7.6.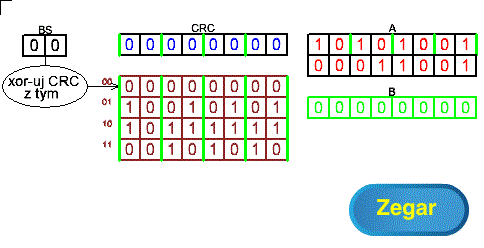
Rys. 7-6
Metoda tablicowa bezpośrednia dla przesunięć 2-bitowych ANIMACJA
Wiadomość 2-bajtowa z rejestru A przechodzi tu przez rejestr CRC skokami 2-bitowymi. Na końcu w ten sam sposób przechodzi bajt z zerami z rejestru B. Przypominam że rejestry BS, CRC, A,B można traktować jak jeden wspólny rejestr BS_CRC_A_B w którym dane przesuwane są w każdym impulsie zegarowym o 2 bity w lewo. Każdemu przesunięciu towarzyszy xor-owanie danych z CRC z danymi wskazanymi przez BS. Nawet gdy BS=00 to też jest xor-owanie, tyle tylko że ta operacja nic nie zmienia.
W rozdz. 8 przekonasz się, że te działania do złudzenia przypominają przesunięcia 8-bitowe. Z tym, że 2 bity idealnie odpowiadają 8 bitom i “przełożenie” jest prawie 1:1. A dlaczego “prawie”? Bo tablica będzie miała 256 adresów jako że 8-bitowe BS daje 256 różnych kombinacji bitów.
Rozdz. 7.5 Metoda tablicowa “lewa” z podwójnym xor-owaniem dla przesunięć 2-bitowych
Sorry Gregory za prywatne nazwy, inne niż np. “Metoda maglowanej tablicy” w super artykule “CRC doda Ci pewności siebie” pana Jarosława Dolińskiego. Tablicowa-wiadomo, “lewa” bo bity skaczą w lewo, a “ podwójne xor-owanie” to za chwilę będziesz wiedział.
Rys. 7-7
Metoda tablicowa “lewa” z podwójnym xor-owaniem dla przesunięć 2-bitowych ANIMACJA
W metodzie bezpośredniej 2 bity bezpośrednio przechodziły z CRC do BS. Tu też przechodzą z CRC do BS ale są dodatkowo xor-owane z początkowymi 2 bitami z pamięci A. Wiadomość A omija tu CRC, inaczej-nie przechodzi przez CRC. Zauważ, że dzięki takiej zasadzie znikają rejestr B z zerami i początkowy “pusty” przebieg z zerami tak jak w rozdz. 7.4. Tak jest chyba “eleganciej”, chociaż kosztem tego dodatkowego xor-owania CRC przez dane z wiadomości A. Mam tu uczucia mieszane. Przecież rejestr A to w praktyce tysiące bajtów. Czyli “pusty” przebieg i rejestr B nie mają wpływu na transmisje. Być może to dodatkowe xor-owanie występuje w tym samym cyklu jak jedno xor-owanie z Rozdz. 7.4 i dlatego nie wpływa na szybkość transmisji. I tak chyba jest, bo metody bezpośredniej raczej nie stosuje w praktyce, albo rzadziej.
W animacji przekonasz się, że obliczone końcowe CRC=11100110 jest oczywiście takie samo jak w rozdz. 7.2 i 7.4!
Rozdz. 7.6 Metoda tablicowa “prawa” z podwójnym xor-owaniem dla przesunięć 2-bitowych
Nazwa mówi za siebie.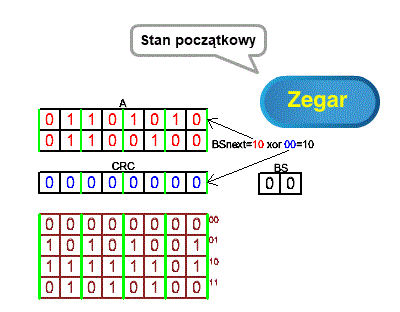
Rys. 7-8
Metoda tablicowa “prawa” z podwójnym xor-owaniem dla przesunięć 2-bitowych ANIMACJA
O co chodzi, skoro poprzednia metoda wydaje się być już bez zastrzeżeń? Wróć na chwilę do Rozdz. 7.1. Była tam mowa o tym, że wszystkie bity wychodzące na zewnątrz czyli do sieci, przechodzą przez tzw. UART. A ten najczęściej (a może zawsze?) traktuje bity prawe jako bardziej znaczące. Czyli np. bajt=00000001 będzie potraktowany jako 128, a bajt=10000000 jako 1. Odwrotnie niż jesteśmy do tego przyzwyczajeni. Trudno, tak zostały te UART-y zaprojektowane 50 lat temu i nic na to nie poradzimy. A my chcemy chcemy żeby 00000001 było traktowane jako 1. Można np. zmodyfikować metodę “lewą” w ten sposób, żeby “obrócić” każdy bajt przed wysłaniem i wszystko będzie ok. Okazuje się, że po pierwsze nie każdy mikroprocesor ma taki prosty wydawałoby się rozkaz. A po drugie, jeżeli już go ma, to jego wykonanie trwa trochę. A to opóźnia transmisję! I od tego jest właśnie metoda “prawa”. Tu dane wprowadzanego ćwierćbajtu są “ludzkie”, tzn. lewy bit jest ważniejszy od prawego. W stanie początkowym na Rys. 7-7 pierwszym wprowadzanym ćwierćbajtem do sieci i do BS-a modyfikującego CRC jest 10 czyli 2 a nie 1! Czyli cały bajt z A=01101010 będzie potraktowany przez UART jak 10101001 z Rozdz. 7.5. I o to nam chodziło!
Ale do tego muszą być jeszcze spełnione 3 dodatkowe warunki:
1. Wszystkie wiersze w tablicy muszą być “obrócone” względem środkowej osi.
2. Musi być “obrócony” też stan początkowy rejestru CRC.
3. Obliczone końcowe CRC też jest “obrócone”.
ad. 1 tu np. wiersz 3 11111101 jest “obrócony” względem wiersza 3 10111111 z Rozdz. 7.5
ad. 2 tu początkowe CRC=00000000 jest “obrócone” względem CRC=00000000 z Rozdz. 7.5. W przypadku zerowego CRC “obrócenie” nic nie zmienia, ale są algorytmy CRC które mają niezerowe początkowe CRC.
Zrób animację i przekonasz się, że obliczone CRC będzie takie samo jak w Rozdz. 7.2 i 7.4 czyli CRC=11100110. Przecież wiadomości wejściowe A=10101001 00011001 są takie same, a tablice w Rozdz. 7.4 i 7.5 zostały zbudowane na podstawie tego samego
“dzielnika”=10010101 z Rozdz. 7.2!
A tu gucio! CRC=10010101 jest inne niż w Rozdz. 7.2 i 7.4. I tu jest właśnie grzech pierworodny tego kursu. Liczę teraz na pomoc mądrzejszych ode mnie Czytelników. Pierwszemu który wskaże błąd i policzy “prawą” metodą, że CRC=11100110 stawiam ośmiopak Żywca!
Proszę tylko przesłać na email numer konta bankowego. Nie jest to co prawda nagroda Nobla, ale ten miał trochę większe możliwości.
Rozdz. 7.7 Software czyli program obliczający CRC
Rozdz. 7.7.1 Wstęp
Wiadomość do wysłania znajduje się w rejestrze A. Tablice zostały stworzone na podstawie rozdz. 7.4, z tym że tablica “prawa” (rozdz. 7.6) jest nieco inna niż “lewa” i “bezpośrednia”. Same programy budujące tablice pozostawiam ambitniejszym czytelnikom. Użyty został pewien rodzaj pseudojęzyka, który prawie nie wymaga komentarza.
Rozdz. 7.7.2 Program dla metody tablicowej bezpośredniej z przesunięciami 2-bitowymi
Rejestry BS CRC A B z Rys.7-6 tworzą wspólny rejestr przesuwny BS_CRC_A_B. Instrukcja Wpisz 2 bity z A do CRC w lewo naszego pseudojęzyka, wpisuje nie tylko 2 początkowe bity z A do CRC, ale przesuwa też cały rejestr BS_CRC_A_B o 2 bity w lewo. Następnie CRC jest xor-owane przez wiersz tablicy wskazany przez BS.
B=0
Dopóki A niepuste
{ Wpisz 2 bity z A do CRC w lewo
CRC=CRC xor tablica(BS) }
Po wyjściu z pętli CRC będzie zawierało obliczoną “resztę”.
Rozdz. 7.7.3 Program dla metody tablicowej “lewej” z podwójnym xor-owaniem i przesunięciami 2-bitowymi
Nie ma “zerowego” rejestru B
Dopóki A niepuste
{
BS=2 początkowe bity A xor 2 początkowe bity CRC
Przesuń A o 2 bity w lewo
Przesuń CRC o 2 bity w lewo
CRC=CRC xor tablica(BS)
}
Po wyjściu z pętli CRC będzie zawierało obliczone CRC czyli “resztę”.
Rozdz. 7.7.4 Program dla metody tablicowej “prawej” z podwójnym xor-owaniem i przesunięciami 2-bitowymi
Pamiętaj o uwagach dotyczących tablicy i CRC w rozdz. 7.6! Zwłaszcza że ćwierćbajty w A są “obrócone” , ale bity w ćwierćbajtach już nie! Dzięki temu programista nie musi “obracać” każdego ćwierćbajtu przed wysłaniem go do UART-u.
Dopóki A niepuste
{
BS=2 początkowe bity A xor 2 początkowe bity CRC
Przesuń A o 2 bity w prawo
Przesuń CRC o 2 bity w prawo
CRC=CRC xor tablica(BS)
}
Obróć CRC
Po wyjściu z pętli CRC będzie zawierało obliczone CRC czyli “resztę”.
