Podstawy automatyki

Rozdz. 13. Równania różniczkowe

Rozdz. 13.1 Wstęp
Jest to pierwsze podejście do równań różniczkowych. Będziemy analizować proces napełniania zbiornika bez dziury i z dziurą w dnie. Pojawią się wtedy proste równania różniczkowe. Będzie sporo opisów i temat nie jest najłatwiejszy. Spróbuj się jednak z nim zmierzyć. Gdyby mimo wszystko były problemy, to wywieś białą flagę i czytaj dalej od rozdziału 15. Traktuj tylko wtedy transmitancję G(s) jako „coś”, co zamienia sygnał wejściowy x(t) na wyjściowy y(t), a nie jako odpowiednik równania różniczkowego.

Rozdz. 13.2 Napełnianie zbiornika bez dziury

Rys. 13-1
Przepływ Q=1litr/sek oznacza, że z kranu w ciągu 1 sekundy wypływa 1 litr wody.
Ogólnie – Przepływ to objętość cieczy jaka wypłynęła z kranu w czasie 1 sekundy. Jednocześnie jest to objętość cieczy V(t), o jaką wzbogacił się zbiornik w czasie 1 sekundy.
Łatwo więc obliczymy objętość V(t) po czasie t lub wysokość h(t). Ale tylko pod warunkiem, że przepływ jest stały w czasie! Czyli nie kręcimy zaworem, tak jak wielokrotnie robiliśmy to z suwakiem.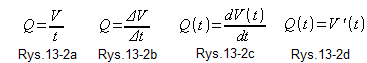

Rys. 13-2
Rys. 13-2a to wzór na przepływ, ale pod warunkiem że nie kręcimy zaworem. Czyli jest stały.
A gdy nie jest stały? Wtedy pojawia się wzór przybliżony na przepływ chwilowy (Rys. 13-2b), gdzie ΔV jest objętością cieczy w zbiorniku która wypłynęła w czasie Δt. Wzór ten jest tym dokładniejszy, im krótszy jest czas Δt. Wtedy przepływ Q(t) staje się coraz bardziej podobny do pochodnych przedstawionych na Rys. 13-2c lub Rys. 13-2d. Są to najprostsze formy równań różniczkowych.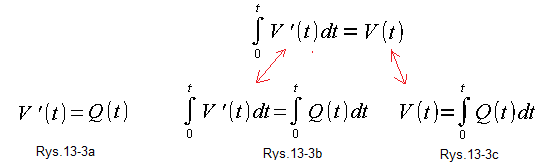

Rys. 13-3
Rys. 13-3a to równanie różniczkowe którego „wiadomą” jest funkcja przepływu Q(t) a niewiadomą jest funkcja objętości V(t). Nie wiemy jeszcze jaki jest przebieg V(t) ale wiemy, że jej pochodna z V(t) jest przepływem Q(t). Jak znaleźć funkcję V(t) która spełnia to równanie?
W przypadku gdy Q(t) jest stałe, tak jak na Rys. 13-1 Q=1/litr/sek to sprawa jest banalna. V(t)=Q*t. Typowa funkcja liniowa. V(t=0)=0, V(t=1 sek)=1 litr, V(t=2 sek)=2 litry itd.
A gdy Q(t) jest zmienne w czasie? Wtedy rozwiązujemy równanie różniczkowe z Rys. 13-3a metodą scałkowania obu stron.
Rys. 13-3b to „scałkowane obustronnie” równanie Rys. 13-3a
Rys. 13-3c to wynik „scałkowania obustronnego”. Czerwone strzałki i Rys. 12-7c z rozdz. 12 mówią dlaczego.
Tak a propos. Już w szkole podstawowej w zadaniach typu „Pociąg jedzie z miasta A do B ze stałą prędkością…” rozwiązywałeś równania różniczkowe! Prędkość V to pochodna drogi S. Gdy prędkość jest stała to wzór S=V*t jest rozwiązaniem równania różniczkowego S'(t)=V. Wróćmy jednak do zbiornika bez dziury jako przykładu najprostszego równania różniczkowego

Rys. 13-4
Wzór V'(t)=Q(t) to innymi słowy „przepływ chwilowy Q(t) pochodna przepływu V'(t)” , bardziej obrazowo- prędkości narastania objętości V'(t). Jak napełniasz wannę to prędkość narastania objętości V'(t) bardziej kojarzy się z prędkością narastania poziomu w wannie h'(t). Spróbujmy wzór ogólny V'(t)=Q(t) uprościć jak się da.
Przy założeniu że:
– wanna jest prostopadłościanem o pow. 1 m²
– w chwili t=0 odkręciliśmy błyskawicznie kran i od tej pory jest stały przepływ Q=1 litr/sek
wanną rządzi równanie różniczkowego
h'(t)=1.25(t)
gdzie 1.25(t) to skok jednostkowy przepływu od 0 do 1.25 litr/sek, a bardziej ogólnie y'(t)=x(t) gdzie x(t) to wejście a y(t) jest wyjściem.
Naszym celem jest znalezienie takiej funkcji h(t) która spełnia to równanie. Scałkujmy więc obie strony równana tak jak na Rys. 13-3c

Rys. 13-5
Rys. 13-5a-równanie różniczkowe opisujące napełniane zbiornika, gdzie wyjściem poziom wody h(t)
Rys. 13-5b-scałkowanie obu stron wersji z Rys. 13-5a
Rys. 13-5c-rozwiązanie jako efekt powyższego scałkowania
Rys. 13-5d-definicja skoku przepływu 1.25(t) jako sygnału wejściowego
Rys. 13-5d-definicja rozwiązania jako narastającej piły poziomu h(t)
To bądźmy jeszcze większe paniska i rozwiążmy równanie różniczkowe Xcos-em  z darmowego programu Scilab.

Rys. 13-6
Z rozdziału 12 np. Rys. 12-14 wiemy, że na wyjściu członu całkującego jest całka z wejścia i vice versa na wejściu jest pochodna z wyjścia. Dlatego z czystym sumieniem stwierdzamy że x(t)=y'(t) czyli 1.25(t)=h'(t). Tak więc schemat z Rys. 13-6 rozwiązuje równanie różniczkowe h'(t)=1.25(t). Sprawdźmy to:
W chwili t=0 błyskawicznie został otwarty zawór. Od tej pory przepływ Q(t)=1.25 litr/sek jest stały. Z przebiegu wynika, że poziom wody podnosi się ze stałą prędkością zgodnie ze wzorem h(t)=1.25*t(t), gdzie poziom podany jest w milimetrach. np. W 10 sekundzie poziom wody w zbiorniku wynosi h=12.5 mm.* Przypominam, że dla t<0 (ujemnego) x(t)=y(t)=0.
*Nie przejmuj się dziwnymi rozmiarami zbiornika w którym S=1m2 a poziom h(t) podniesie się ok. 12.5mm. Tak wyszło.

Rozdz. 13.3 Napełnianie zbiornika z dziurą k=1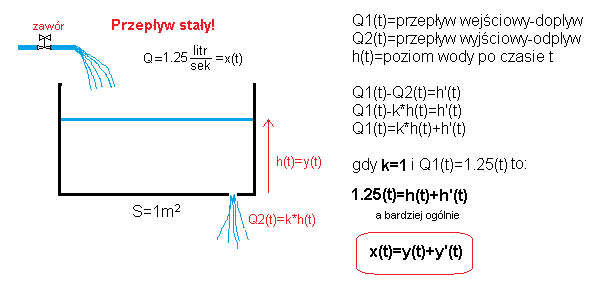

Rys. 13-7
W odróżnieniu od Rys. 13-4 poziom wody będzie podnosił się coraz wolniej ze względu na odpływ Q2(t). Poprzednio prędkość podnoszenia się poziomu h'(t) była proporcjonalna do przepływu wejściowego Q(t), tak teraz będzie proporcjonalna do różnicy przepływów Q1(t)-Q2(t). Wiemy, że im wyższy poziom wody, tym większy odpływ. Czyli Q2(t)=k*h(t). Pytanie. Jak k zależy od powierzchni dziury? Jasne, im większa dziura tym większe k! Gdy k=0 , to nie ma dziury i jest przypadek poprzedni czyli Rys. 17-4.
Załóżmy, że wielkość dziury odpowiada k=1.
Z rysunku wynika że w/w zbiornik opisany jest równaniem różniczkowym:
1.25(t) = h'(t) + h(t)
a bardziej ogólnie:
x(t)=y'(t)+y(t)
Spróbujmy przewidzieć jaka funkcja h(t) spełnia to równanie? Na palcach już chyba się nie da. Nie pomoże też całkowanie dwóch stron równania, jak dla równania x'(t)=y(t). Są oczywiście metody, ale ich jeszcze nie znamy. To może chociaż częściowo uda nam się przewidzieć jak zachowuje się poziom h(t) w czasie?
Na pewno dla t=0 h(t)=0. Wtedy 1.25=h'(t). Nachylenie (pochodna!) h(t)=1.25. Za chwilę h(t) już nie jest zerowe i h'(t)=1.25(t)-h(t) . Nachylenie h(t) się trochę zmniejszy. Poziom rośnie trochę wolniej, a odpływ Q2(t) trochę wzrośnie. A kiedy poziom się ustali? Wtedy gdy co wlata to wylata. Czyli gdy Q2(t) = Q1(t). Jak poziom się ustali to h'(t)=0 i h(t)=1.25 mm. Czy nie przypomina nam to członu inercyjnego?. W dodatku okaże
Rozwiążmy równanie różniczkowe  przy pomocy schematu z członem całkującym. Czyli skorzystamy z aplikacji Xcos darmowego programu SCILAB.

Rys. 13-8
Dla każdego członu całkującego 1/s jego wejście jest pochodną wyjścia. I to nie ważne, czy wejście jest pojedynczym sygnałem jak na Rys. 13-6, czy różnicą 2 sygnałów jak na Rys. 13-8. Może być nawet dowolną funkcją kilku sygnałów, np. iloczynem. Dlatego człon całkujący idealnie nadaje się do rozwiązywania takich równań różniczkowych w których występuje y(t) i jego pochodna y'(t).
Czyli h'(t)=1.25(t)-h(t) , inaczej 1.25(t)=h'(t)+h(t) a ogólnie x(t)=y'(t)+y(t)
Schemat da takie y(t) gdzie w każdej chwili jest spełnione równanie x(t)=y(t)+y'(t).
Wygląda na to, że zbiornik z dziurą jest członem inercyjnym. Z wykresu wynika, że stała czasowa T=1 sek. Po czasie 6…7 sekund zbiornik osiągnie stały poziom h=1.25 mm.
Zauważ, że cały czas spełnione jest równanie 1.25(t)=h'(t)+h(t). Na początku pochodna h'(t) jest największa i równa 1.25 mm/sek a poziom h(0)=0. Potem nachylenie maleje a poziom rośnie. W stanie ustalonym nachylenie czyli h'(t)=0 i h(t)=1.25..
Mały komentarz.
Po ok. 7 sek. poziom wody ustalił się na h=1.25 mm. Bardzo mały ten poziom, na dnie jest tylko 1.25mm! Widocznie dziura jest tak duża, że dno stanie się tylko mokre. Zmniejszmy dwukrotnie powierzchnię dziury. Czyli dajmy k=0.5. Czy poziom będzie 2 razy większy?

Rozdz. 13.4 Napełnianie zbiornika z mniejszą dziurą k=0.5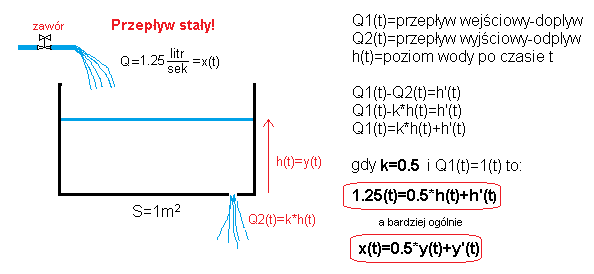

Rys. 13-9
Teraz dziura jest mniejsza (k=0.5) i zbiornik opisany jest równaniem różniczkowym:
1.25(t)=h'(t)+0.5*h(t)
a bardziej ogólnie:
x(t)=y'(t)+0.5*y(t)
Porównaj z poprzednim zbiornikiem i znajdź różnicę.
Równanie różniczkowe rozwiążemy przy pomocy schematu z członem całkującym

Rys. 13-10
Tak jak przypuszczaliśmy, poziom ustalony będzie 2 razy większy. Tu y=2.5 mm. Co do dynamiki, to układ jest w dalszym ciągu inercyjny ale ma 2 razy większą stałą czasową–>T=2 sek.
Uwaga.
Założyliśmy, że odpływ wody jest proporcjonalny do poziomu Q2(t) = k*h(t). Rzeczywiście, gdy w wannie wyciągnę korek, to na początku woda spływa najszybciej, potem (gdy poziom jest mniejszy) to spływa wolniej! Jest to jednak tylko pierwsze przybliżenie! Tak na prawdę to odpływ Q2(t) jest proporcjonalny do pierwiastka z poziomu! Sprawdźmy więc ten dokładniejszy model matematyczny.

Rozdz. 13.5 Napełnianie zbiornika dziurą k=1-dokładniejszy model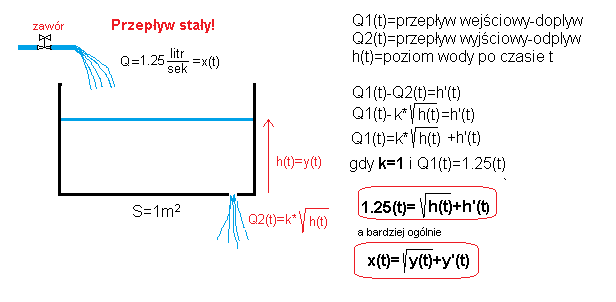

Rys. 13-11
Z powyższych równań wynika, że odpływ Q2 jest proporcjonalny do pierwiastka z poziomu h(t). Powstało równanie, które jest przykładem nieliniowego równania różniczkowego, zwykle trudniejsze do rozwiązania niż rozpatrywane wcześniej liniowe. Na szczęście dla Xcosa to żaden problem.

Rys. 13-12
W pierwszej chwili wygląda to na człon inercyjny. Ale nim nie jest! W porównaniu do rozdz.13.3 gdzie też było k=1, ciecz osiągnęła większy poziom ustalony h=1.5625 mm. Ten poziom można też wyznaczyć teoretycznie. Wtedy dopływ Q1(t) równy jest odpływowi Q2(t).
Jeszcze jedno. Pamiętacie, że założyłem skok x(t)=1.25(t) zamiast tak jak zwykle x(t)=1(t). Dlaczego? Bo akurat dla x(t)=1(t) poziomy ustalone dla dla zbiornika „z dziurą” i „bez” wyjątkowo są takie same h=1mm! . Czytelnik mógłby pomyśleć, że tak jest dla dowolnego x(t).

Rozdz. 13.6 Więcej o równaniach różniczkowych
W zbiorniku bez dziury poznaliśmy najprostsze równanie różniczkowe 1.25(t)=h'(t)
Zbiornik z dziurą opisywany jest już przez trudniejsze równanie różniczkowe 1.25(t)= h'(t)+h(t)
Ostatnie równanie możemy uogólnić na x(t) = a1*y'(t) + a0*y(t) gdzie:
– x(t) – sygnał wejściowy – odpowiednik 1.25(t)
– y'(t) – pochodna sygnału wyjściowego – odpowiednik h'(t)
– y(t) – sygnał wyjściowy – odpowiednik h(t)
– a0, a1 stałe współczynniki – w równaniu 1.25(t) = h'(t) + h(t)–> a1=a0=1

Równanie można jeszcze bardziej uogólnić na większy stopień pochodnej – np 3.stopnia.
– x(t) = a3*y”'(t) + a2*y”(t) +a1*y'(t) +a0*y(t)
a0, a1, a2, a3 to stałe współczynniki.

Skoro tak ładnie idzie nam uogólnianie, to pochodne mogą być też po lewej stronie np.
– b3*x”'(t) + b2*x”(t) + b1*x'(t) + b0*x(t)= a3*y”'(t) + a2*y”(t) + a1*y'(t) + a0*y(t)

Jeszcze raz podkreślam. Wszystkie współczynniki muszą być stałe i wtedy jest to równanie różniczkowe liniowe.
Przykładem takiego równania jest
– x”(t) + 3*x'(t) + 2*x(t)= 2*y”'(t) -3*y”(t) + 4*y'(t) + 2*y(t)
Przykładem równanie różniczkowego nieliniowego był dokładniejszy model zbiornika z dziurą z rozdz.13.5 lub np.
y(t)*x”(t) + t*x(t) = y(t)”+x(t)*y'(t) + y(t)
Takimi równaniami nie będziemy się zajmować. Dlatego każde równanie różniczkowe będzie dla nas równaniem różniczkowym liniowym
A jak je rozwiązać? Czyli jak znaleźć funkcję y(t) znając funkcję x(t)? Okazuje się, że wiele razy już to robiłeś w tym kursie. Sygnałem wejściowym x(t) był najczęściej skok jednostkowy 1(t), rzadziej sygnał narastający liniowo lub kwadratowo.
Wtedy Xcos na podstawie:
– schematu blokowego
– sygnału wejściowego x(t)
stworzył odpowiednie równanie różniczkowe liniowe, które rozwiązał obliczając y(t) i pokazał na wykresie.
Wiadomo, że równania różniczkowe można też rozwiązać na papierze. Matematycy robili to od dawna, gdy nie było jeszcze komputerów i Xcosa.
W następnym rozdziale zajmiemy się rachunkiem operatorowym, jako narzędziem do do rozwiązywania równań różniczkowych liniowych.