Podstawy automatyki

Rozdz. 8 Człon całkujący z inercją

Rozdz. 8.1 Wstęp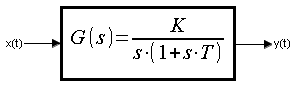

Rys. 8-1
Transmitancja członu całkującego z inercją.
Pamiętasz człon całkujący? Skok x(t) na wejściu powodował wzrost sygnału wyjściowego y(t) do nieskończoności ze stałą prędkością. Podkreślam. Ze stałą prędkością od początku skoku x(t).
Człon całkujący z inercją też dąży do nieskończoności. Ale robi to trochę inaczej. Na początku skoku x(t) „rozpędza” się począwszy od prędkości V=0 i skończywszy na pewnej ustalonej V=const. Jest więc dokładniejszym przybliżeniem np. siłownika niż idealny człon całkujący.

Rozdz. 8.2 k=1 T=3 sek z suwakiem i bargrafem
Znowu zaczniemy od bargrafu aby wstępnie zapoznasz się z dynamiką.
Członem inercyjnym jest szeregowe połączenie całkującego 1/sTi i inercyjnego 1/(1+sT). Tu Ti=1sek i T=3sek

Rys. 8-2
Suwak wstępnie ustawiony jest na 0. Podałem nim x(t)=0.1 =+max.  Zaobserwujesz przebiegi podobne jak dla wcześniej badanego członu całkującego. Też musisz podać 0 na wejście, żeby zatrzymać sygnał wyjściowy. Dla ustawienia 0* przyda się miernik cyfrowy. Jeżeli udało Ci się zatrzymać y(t) (nie rośnie i nie maleje), to ujawni się typowa cecha regulatorów PI lub PID. Ustalone wyjście regulatora yr(t) jest różne od zera, chociaż na wejściu jest zero!
Przebiegi są podobne jak dla członu całkującego , ale nie takie same! Mam nadzieję, że widzisz inercję. Zwłaszcza, gdy podasz +max-a i za chwilę -max-a. Zauważysz, że sygnał przez krótki czas nadal rośnie, chociaż x(t)=0 a nawet maleje! Zjawisko inercji będzie wyraźniejsze w następnym eksperymencie z oscyloskopem.
*Trudno jest ustawić dokładne 0 na mierniku cyfrowym. Jest to raczej sygnał bliski 0, np. x(t)=+0.002. Oznacza to, że y(t) “prawie się zatrzyma” tzn. y(t) bardzo wolno narasta.

Rozdz. 8.3 Ti=1sek i T=3 sek ze skokiem i oscyloskopem
Rys. 8-3
Człon całkujący z inercją to szeregowe połączenie członu całkującego 1/sTi  i inercyjnego1/(1+sT). Ti=1sek i T=3sek

Rys. 8-3
Na wejściu jest skok x(t)=1.Sygnał yp(t) to przebieg za całkującym, y(t) to wyjście. Na początku wyraźnie widać inercję T=3sek. W stanie ustalonym obydwa sygnały rosną z taką sama prędkością. Człon całkujący z inercją jest przykładem tzw. układu astatycznego. Przy niezerowym x(t), sygnał y(t) rośnie albo maleje.  Dla tego członu całkującego Ti=1sek  jako czas po którym yp(t) zrówna się z x(t). Jest to również czas, po którym w stanie ustalonym y(t) wrośnie o wartość skoku x(t)=1, czyli też Ti=1sek.
W stanie ustalonym, tzn. po ok. 18sek, sygnał wyjściowy y(t) jest opóźniony o T=3sek.

Rozdz. 8.4 Ti=1sek T=3 sek z pojedynczym impulsem prostokątnym i oscyloskopem
Na człon całkujący z inercją działa pojedynczy impuls prostokątny.

Rys. 8-4
Jest to dokładniejsze przybliżenie członu wykonawczego – silnika z przekładnią jako idealnego członu całkującego, którego ramię może sterować położeniem zaworu. Ten przykład omówiony został w rozdz. 4. Człon Całkujący. Tu natomiast uwzględniamy jeszcze inercję. Czarne x(t) wejście to napięcie na silniku a czerwone wyjście y(t) to położenie trzpienia zaworu. Nie muszę dodawać, że inercja, zawierająca w sobie głównie bezwładność mechaniczną + trochę bezwładności elektrycznej- inukcyjności, „psuje” jakość urządzenia. W siłowniku trudno byłoby wyodrębnić sygnał yp(t) -bezpośrednio za całkującym. Jest to możliwe tylko w modelu, tak jak na Rys. 8-4.

Rozdz. 8.5 Człon całkujący z inercją k=1 T=1.25 sek z dodatnim i ujemnym impulsem prostokątnym i oscyloskopem
Zobaczymy jak działa siłownik, który „szuka” swojego położenia.
Tzn. raz kręci w jedną stronę, a raz w drugą, aż znajdzie zadane przez regulator położenie i zatrzyma się.
Na Człon całkujący z inercją działają więc kolejno impuls prostokątny dodatni i ujemny.

Rys. 8-5
Niebieskie yp(t) to idealny siłownik bez inercji. Czerwone y(t) to prawdziwy siłownik z inercją.
Siłownik z Rys. 8-4 z inercją T=3 sek kupił biedny Klient. Teraz natomiast Klientem jest Panisko, które chce żeby siłownik szybko reagował. Dlatego sprzedałem siłownik z mniejszą  inercją T=1.25 sek. Efekty są widoczne. Siłownik szybciej dojdzie do prędkości ustalonej. Dlatego szybciej też osiągnie ustalone y(t). Najpierw dodatni impuls ustawił trzpień na wartość y(t)=8, siłownik trochę postał (bo tak sobie życzył np. regulator) a potem ujemnym impulsem ustawił trzpień na y(t)=4.