Scilab

Rozdział 13 XCOS-Jak działa Ujemne Sprzężenie Zwrotne?

Rozdz. 13.1 Jak Działa Sprzężenie Zwrotne?
W Układach Regulacji Automatycznej najważniejsze jest zrozumienie zasady Sprzężenia Zwrotnego. To musi być dla oczywiste i intuicyjne jak jazda na rowerze! Występuje wtedy, gdy sygnał wyjściowy y(t) wraca z powrotem na wejście.

Rys.13-1
Rys. 13-1a
Sygnał y(t) z wyjścia wraca bezpośrednio na wejście. Ale co jest przyczyną, a co skutkiem? Czy jajko było pierwsze czy kura? Że już nie powiem o bardziej egzystencjalnych pytaniach. Potraktujmy więc schemat jako ciekawostkę.
Rys.13-1b
Czyli potrzebny jest jakiś kontakt ze światem zewnętrznym. Realizowane jest to jako obliczanie różnicy e(t)=x(t)-y(t) w tzw. węźle porównującym. Jest to najważniejszy schemat w automatyce, ponieważ y(t) stara się naśladować x(t). Dlatego musisz go dobrze zrozumieć!
Rozdz. 13.2 Jak działa dodatnie sprzężenie zwrotne z Układem Inercyjnym?.
Na wejście podawana jest suma sygnałów e(t)=x(t)+y(t) zamiast różnicy jak na Rys. 13-1b. Jest łatwiejsze do zrozumienia niż ujemne sprzężenie zwrotne i tylko dlatego analizujemy ten przypadek.
Uwaga:
1. Blok Sumatora na poniższej symulacji znajdziesz w palecie Operacje Matematyczne.
2. Krótki impulsik x(t) (substytut impulsu Diraca) w 5 sekundzie zrealizuj np. jako różnicę skoków jednostkowych przesuniętych w czasie o 0.01sek–>2(t-5) i 2(t-5.01).

Rys. 13-2
Na wejście bloku inercyjnego wchodzi suma s(t)=x(t)+y(t). Początkowo x(t)=y(t)=0. Czyli s(t)=0+0 =0 i nic się nie dzieje. Ale w piątej sekundzie pojawia się „szpilka”. Ot, taki mały prztyczek. Sygnał ten przejdzie przez człon inercyjny jako „stłumiona szpilka” o mniejszej amplitudzie i zwiększona 1.5 razy . Na początku ta „stłumiona szpilka” jest tak mała, że nie widać jej na wykresie, ale natychmiast wróci na wejście i ponownie będzie zwiększona 1.5 razy. Znowu wróci i ponownie będzie zwiększona 1.5 razy…itd. Klasyczny efekt lawinowy. Układ od samego początku był niestabilny, chociaż do piątej sekundy nie było tego widać. Ale wystarczył mały „prztyczek”, aby nastąpiła katastrofa.
Uwaga:
Nie zawsze dodatnie sprzężenie zwrotne jest niestabilne jak na Rys.13-2. Spróbuj np. K=0.8 zamiast K=1.5. Zmniejsz tylko Ymax w oscyloskopie z 10 na 0.1, aby zwiększyć wzmocnienie oscyloskopu. Po “prztyczku” układ dojdzie do stanu ustalonego y(t)=0. Zauważ, że teraz o<K<1, w odróżnieniu od Rys.13-2 gdy K>1! Gdybyś zamiast “prztyczka” dał skok, wyjście y(t) doszłoby do y=4.
Rozdz. 13.3 Jak działa ujemne sprzężenie zwrotne z Układem Inercyjnym?.
Czyli jak człon inercyjny z ujemnym sprzężeniem zwrotnym dochodzi do stanu ustalonego. Dotyczy to dowolnych bloków w układzie otwartym (czyli bez sprzężenia zwrotnego),  które w odpowiedzi na skok dają skończoną wartość. Czyli tzw. układów statycznych. Radzę dogłębnie zrozumieć zasadę dochodzenia do pewnej równowagi. To podstawa automatyki Zwłaszcza, że większość autorów podchodzi do tego czysto matematycznie. Z wyliczeń wynika, że powstanie jakiś tam uchyb ustalony e=x-y. Tzn. różnica między ustaloną wartością zadaną x a na wyjściu y.

Rys.13-3
Człon inercyjny z ujemnym sprzężeniem zwrotnym.
Na oscyloskop podane są sygnały:
– wyjściowy y(t)
– cel K*e(t)  (K=5)
Sygnał y(t) dąży do celu K*e(t) ,który jest zmienny w czasie.  „Siłą napędowa”, która usiłuje zbliżyć do siebie cel K*e(t) i y(t) też jest różnica U=K*e(t)-y(t) w postaci pionowej zielonej kreski na prawym rysunku. Im bardziej różnica U – „siła napędowa” jest większa tym silniej linie cel K*e(t) i y(t) „lgną” do siebie.
Wyjście y(t) dąży do stanu równowagi y(t)=K*e(t) w którym znika „siła napędowa U”-pionowa zielona kreska 
A kiedy y(t) przestanie rosnąć? Albo inaczej-kiedy będzie stan ustalony. Wtedy, gdy cel zostanie osiągnięty, gdy siła napędowa (pionowa zielona kreska U) zniknie! Czyli gdy y(t)=K*e(t).
Tak jest nie tylko dla członu inercyjnego, ale dla każdego członu dynamicznego z ujemnym sprzężeniem zwrotnym, który w stanie ustalonym ma wzmocnienie K.  Eksperyment potwierdza coś bardzo ważnego w automatyce. Tak jak wytrącone z równowagi wahadło wróci do stanu ustalonego którym jest najniższe położenie
Tak układ stabilny z ujemnym sprzężeniem zwrotnym wróci do stanu y(t)=K*e(t)
Z powyższego równania tj. y(t)=K[x(t)-y(t)] po szkolnych przekształceniach wynika y(t)=K*x(t)/(K+1)*. Czyli dla bardzo dużego wzmocnienia K i wstanie ustalonym  y(t)≈x(t). Czyli wyjście y(t) stara się naśladować wejście x(t). Jest to najważniejszy cel automatyki,
Człon inercyjny jest przykładem tzw. obiektu statycznego. Tj. takiego który nie ma w sobie członu całkującego. Tu zrozumienie zasady, że “wyjście y(t) stara się naśladować wejście x(t)” nie było najłatwiejsze. W przeciwieństwie do tzw. obiektów astatycznych w których wyjście y(t) w stanie ustalonym jest idealnie równe wejściu x(t). Przekonasz się w rozdz. 13.4.
*Na wszelki wypadek pokażę te przekształcenia w  w Rozdz. 13.5

Rozdz. 13.4 Jak człon całkujący z ujemnym sprzężeniem zwrotnym dochodzi do stanu ustalonego?
Jeżeli obiekt, np. człon całkujący z inercją, ma w sobie człon całkujący to jest tzw. obiektem astatycznym. Tym bardziej będzie nim “czysty” człon całkujący. 

Rys. 13-4
Widzisz jak człon całkujący dochodzi do stanu ustalonego y(t)=x(t)=1. Porównaj z Rys. 13-3  z członem inercyjnym który należy do statycznych. W nim „siłą napędową” która dąży do stanu równowagi było 5*e(t)-y(t). Tu natomiast siłą napędową jest uchyb e(t). Prostota jest piękna!
Gdy x(t)>y(t) (inaczej e(t)>0) to y(t) rośnie jak w każdym porządnym członie całkującym. Dodam jeszcze, że rośnie z coraz mniejszą prędkością bo e(t) cały czas maleje. W stanie ustalonym ta prędkość jest oczywiście zerowa. Wtedy y(t)=x(t)=1 i e(t)=0

Rozdz. 13.5 Wnioski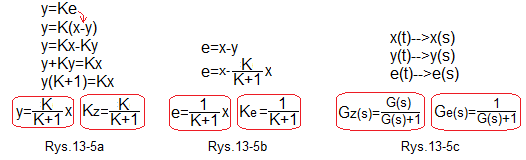

Rys.13-5
Zależność między wejściem, wyjściem i uchybem.
Rys.13-5a
Zależność  między y i x oraz wzmocnienie Kz układu zamkniętego w stanie ustalonym.
Rys.13-5b
Zależność  między uchybem e i x oraz wzmocnienie uchybowe Ke układu zamkniętego w stanie ustalonym.
Rys.13-5c
Zależność  między transformatami wejścia x(s), wyjścia y(s) i uchybu e(s) oraz transmitancja układu zamkniętego Gz(s) i uchybowa Ge(s). Z nich można uzyskać przebiegi czasowe y(t) i e(t).
Wnioski
Wzory z Rys.13-5 są uniwersalne. Dotyczą układów z i bez członów całkujących, czyli układów astatycznych i statycznych.
Jakie jest wzmocnienie w stanie ustalonym przy skoku układu astatycznego, czyli zawierającego człon całkujący? Na wejściu x=1 a na wyjściu y=∞ (nieskończoność). Czyli K=∞. 
Wtedy wzór 13-5a przekształci się w y=x i Kz=1 a wzór 13-5b e=0 i Ke=1
Czyli układ zamknięty zawierający człon całkujący może zapewnić w stanie ustalonym uchyb zerowy. Czyli stan w którym wyjście y “słucha się” wartości zadanej x.