Podstawy Automatyki

Rozdz. 23 Regulacja P

Rozdz. 23.1 Wstęp
Ja tylko w kwestii formalnej – jak w sejmie. Długość tego i następnych rozdziałów dotyczących PID-a straszy  nieco. Ale odwagi! Większość doświadczeń jest powtarzalnych. Po początkowym etapie rozpędzania się, będziesz zasuwał jak Pendolino.
Regulator typu P jest najprostszym regulatorem ciągłym. W następnych rozdziałach zapoznasz się z bardziej wyszukanymi regulatorami typu PI, PD oraz z najbardziej wyrafinowaną opcją – regulatorem PID. Tworzą grupę regulatorów typu PID. Z pewną przesadą można powiedzieć, że regulator to w domyśle regulator PID.
Zbadamy sterowanie regulatorem typu P obiektem:
Jednoinercyjnym K=1, T1=10 sek.
Dwuninercyjnym K=1, T1=5 sek. T2=3 sek.
Trójinercyjnym K=1, T1=5 sek. T2=3 sek. T3=0.5 sek.
Tego typu obiekty często spotyka się w przemyśle, zwłaszcza w chemicznym. Ich stałe czasowe są oczywiście większe. Każdy eksperyment to odpowiedź na skok x(t), a następnie na skok x(t) i zakłócenie z(t). Czas trwania to 1 minuta dla skoku i 2 minuty dla skoku i zakłócenia.

Rozdz. 23.2 Transmitancja Gz(s) i wzmocnienie ustalone Kz układu zamkniętego
Jest to krótkie przypomnienie Rozdz. 16 Jak działa sprzężenie zwrotne?

Rys. 23-1
Na wejścia obiektów
– G(s) w układzie otwartym
– Gz(s) czyli G(s) w układzie zamkniętym
podano skok jednostkowy x(t)=1(t-3), czyli skok x=1 z opóźnieniem To=3sek
Układ Otwarty G(s
G(s) jest obiektem trójinercyjnego  o wzmocnieniu K=10 i stałych czasowych T1=1sek, T2=0.5sek i T3=0.1sek. Z licznika G(s) odczytamy wzmocnienie K=10 w stanie ustalonym. To wzmocnienie jako K=y(t)/x(t) z odpowiedzi na skok x(t) potwierdza teorię. Rzeczywiście w stanie ustalonym, czyli po ok. 20 sek–>y1(t)=10, x(t)=1. Czyli K=10/1=10.
Układ Zamknięty Gz(s)
Czyli objęty ujemnym sprzężeniem zwrotnym. Przedstawiono także wzór na transmitancję układu zamkniętego Gz(s) i wynikający z niego wzór na wzmocnienie w stanie ustalonym Kz. Będziesz to widział w doświadczeniach, jako sygnał wyjściowy y(t)=y w stanie ustalonym gdy x(t)=1 . Np. y=0.91 lub y=0.99.
Przypominam, że wzór na Gz(s) oraz na Kz powstał z założenia, że w stanie ustalonym jest spełnione równanie K*e(t)=y(t).
Wtedy sygnał wyjściowy y(t) stara się naśladować (mniej lub bardziej dokładnie) sygnał wejściowy x(t), tzw. wartość zadaną i jest odporny na zakłócenia. Jest to podstawa automatyki.  Jeżeli nie jest to dla Ciebie oczywiste, to wróć do rozdz.16. Opłaci się.

Rozdz. 23.3 Regulator P z obiektem jednoinercyjnym
Rozdz. 23.3.1 Wstęp
Regulator P ma tylko jedną nastawę-Kp. W rozdz. 22 (Rys. 22-2d) wykazaliśmy, że obiekty statyczne mają przeważnie wzmocnienie K=1. Dlatego Kp regulatora jest jednocześnie wzmocnieniem całego układu otwartego zawierającego regulator i obiekt.
Takie podejście bardzo ułatwia dobór nastaw samego regulatora. Będziemy analizować odpowiedź y(t) na skok x(t) przy różnych nastawach Kp. Najpierw zbadamy sam obiekt. Od tego zaczyna się zawsze dobór nastaw każdego regulatora.
Rozdz. 23.3.2 Badanie obiektu jednoinercyjnego w układzie otwartym

Rys. 23-2
Animacja potwierdza, że jest to człon inercyjny o K=1 i T=10sek
Rozdz. 23.3.3 Regulacja P  Kp=10
Regulator proporcjonalny, inaczej regulator typu P wykonuje najprostszą operację matematyczną.
Mianowicie cały czas obserwuje wyjście y(t) oraz wejście x(t) i oblicza sygnał sterujący s(t):
s(t) = Kp*e(t) = Kp*[x(t) – y(t)]. Tu Kp=10.

Rys. 23-3
Odpowiedź na skok jednostkowy regulatora P gdy Kp=10
Cały rozdz. 16 to powtarzanie  aż do znudzenia, że układy z ujemnym sprzężeniem zwrotnym dążą do stanu ustalonego w którym K*e(t)=y(t). I zmienną w czasie wielkość K*e(t) nazwaliśmy celem do którego dąży y(t).  Ten cel to nic innego jak sygnał sterujący s(t) regulatora typu P.
Obliczone K=0.91 potwierdza się z wykresem. Można to też uzasadnić zwykłą intuicją. Człon inercyjny, którym może być np. układ RC, będzie w równowadze wtedy gdy s(t)=y(t) i dodatkowo nic się „nie rusza”, czyli gdy wykresy s(t) i y(t) są poziome.
Dla t=3 sek wyjście y(t)=0, bo człon inercyjny (np. RC) „ładowany” jest od 0. Początkowo, czyli w 3 sek, sygnał sterujący s(t)=10*(1-0)=10. Oscyloskop obcina przebiegi na poziomie 2 i dlatego nie widzisz s(t)=10. Czyli RC ładowane jest z maksymalną prędkością, co widać zresztą na wykresie. Za „chwilę” pojawi się nieduże dodatnie y(t) i sygnał sterujący s(t)=10*[s(t)-y(t)] oraz prędkość wzrostu sygnału y(t) trochę się zmniejszą. Kiedy y(t) przestanie rosnąć? Wtedy gdy y(t)=s(t). Nastąpi to po ok. 10 sekundzie.
Jeszcze jedno. Przebieg jest podobny do tego poprzedniego rozdziału gdy autor sterował ręcznie. Podobny, ale nie do końca. Wynika to z niedoskonałości człowieka. Przy większym doświadczeniu w sterowaniu ręcznym wykres „ludzki” byłby bardziej podobny.
A gdyby autor to robił precyzyjnie obliczając:
s(t)=10*[s(t)-y(t)] co 0.01 sek
to otrzymałby dokładny przebieg z Rys. 22-3 . Tak to zresztą zrobił program Scilab z którego korzystam przy wszystkich symulacjach. Autor nie był tak dobry w sterowaniu jak Scilab, ale podświadomie sterował wg. algorytmu regulatora proporcjonalnego. Na początku był duży uchyb, to dawał duży sygnał sterujący. Uchyb malał to zmniejszał sterowanie, aż doszedł do stanu ustalonego.
Wzmocnienie Kp=10 regulatora proporcjonalnego spowodowało:
1. 11-krotnie zmniejszenie wzmocnienia do Kz=0.91
2. 11-krotnie zmniejszenie stałej czasowej do Tz=0.91
Tak jest generalnie dla regulacji P. Duże Kp powoduje prawie Kz=1 (zawsze trochę mniejsze od 1!) i zwiększa szybkość działania układu.
Proponuję jeszcze pełny widok przebiegu, bez obciętego sygnału sterującego s(t).
Otrzymasz dokładnie taki sam schemat jak Rys. 23-3. To w czym różnica? W (niewidocznych) nastawach oscyloskopu, które zapewniają pełny widok wszystkich sygnałów, a zwłaszcza sygnału sterującego s(t).

Rys. 23-4
W odróżnieniu od poprzedniego rysunku, widzisz jak duży jest sygnał sterujący s(t) na początku skoku. Tym większy im większe jest wzmocnienie Kp regulatora proporcjonalnego. Dzięki temu sygnał wyjściowy na początku rośnie dużo szybciej niż w układzie otwartym na Rys. 23-2. Porównajmy te przebiegi, żeby docenić dobrą robotę regulatora typu P.

Rys. 23-5
Układ z regulatorem proporcjonalnym jest 11 razy szybszy. Jest to oczywisty plus regulacji proporcjonalnej. Niestety pojawił się uchyb w stanie ustalonym e = 1-0.91=0.09. Jest to typowe dla regulacji proporcjonalnej. Uchyb można zmniejszyć zwiększając wzmocnienie Kp.
Mam nadzieję, że nie dojdziesz do genialnego wniosku.
Układ bez regulacji jest wolniejszy niż z regulacją, ale za to jego uchyb w stanie ustalonym jest zerowy!
Rzeczywiście, wtedy y(t)=x(t). To święta prawda, ale układ bez regulacji jest nieodporny na zakłócenia!
Rozdz. 23.3.4 Regulacja Kp=100
Zbadajmy jeszcze wpływ nastawy Kp regulatora proporcjonalnego na jakość regulacji

Rys. 23-6
Układ jest ewidentnie szybszy i uchyb mniejszy. W stanie ustalonym czerwone y(t) prawie pokrywa się z czarnym x(t) zaś zielony uchyb e(t) jest prawie zerowy Potwierdza to także teoria gdzie w przybliżeniu Kz=0.99 i Tz=0.1 sek. Oscyloskop obcina s(t) na wysokości 2. Dlatego zobaczmy pełen przebieg przy innych nastawach oscyloskopu. Schemat będzie identyczny, ale z innymi nastawami oscyloskopu.

Rys. 23-7
Teraz widzisz całe s(t), za to x(t), y(t) i e(t) są prawie niezauważalne. Przy dużych wzmocnieniach Kp sygnały sterujące osiągają s(t) bardzo duże wartości. Przykładowo – piec w stanie ustalonym wymaga tylko 10 kW mocy a na początku skoku aż 1 MW! Tylko szalony projektant dałby taką moc. Praktycznie będzie to np. 30 kW. Wpłynie to oczywiście niekorzystnie na przebiegi, ale nie tak bardzo, jak 1 MW różni się od 30 kW! Do tematu wrócimy w Rozdz. 30 Wpływ Nieliniowości Na Regulację.
Rozdz. 23.3.5 Podsumowanie obiektu inercyjnego sterowanego przez regulator P
Jest łatwy do sterowania. Zwiększanie parametru Kp nie spowoduje niestabilności ani nawet oscylacji, za to zwiększa dokładność regulacji. Strukturalną stabilność przy dowolnym Kp łatwo udowodnić Hurwitzem lub Nyquistem, którego charakterystyka amplitudowo-fazowa przechodzi tylko przez jedną ćwiartkę.

Rozdz. 23.4 Regulator P z obiektem dwuinercyjnym
Rozdz. 23.4.1 Wstęp
Powtórzymy te same eksperymenty, ale z obiektem dwuinercyjnym. Odpowiedzi mogą być ciekawsze.
Rozdz. 23.4.2 Badanie obiektu dwuinercyjnego w układzie otwartym

Rys. 23-8
Obiekt jest szeregowym połączeniem 2 obiektów jednoinercyjnych o wzmocnieniach K1=K2=1 i stałych czasowych T1=3 sek i T2=5 sek.  Widoczny jest charakterystyczny dla wieloinercyjnych punkt przegięcia. Wyznaczenie stałych czasowych T1,T2 nie jest już takie proste jak dla inercyjnego.
Rozdz. 23.4.3 Regulacja Kp=10

Rys. 23-9
Schemat różni się od Rys. 23-5 tylko innym bardziej skomplikowanym obiektem.
Także stan ustalony wystąpi wtedy, gdy s(t)=y(t), oraz „nic się nie rusza”. Czyli wszystkie pochodne są zerowe. Tak jest po 30 sek . W odróżnieniu od sterowania członem inercyjnym, s(t) chwilami przekracza y(t). Wtedy s(t) staje się mniejsze od y(t), potem znowu przekracza y(t). I tak po kilku “wahadłach” y(t) dojdzie dokładnie do obliczonej wartości ustalonej y=0.91. Sygnał sterujący s(t) ma duże amplitudy “obcinane” przez oscyloskop. Aby zobaczyć całe s(t) powtórzymy eksperyment z innymi nastawami oscyloskopu.

Rys. 23-10
Widać jak szaleje s(t). Duże wartości sygnału sterującego są typowe dla regulacji typu P. Wzmocnienie Kp=10 daje uchyb e(t)=0.09. Ale czy zadowoliłby Ciebie regulator, któremu nastawisz wartość zadaną x(t)=100ºC a on daje tylko 91ºC. Niestety taka jest uroda regulacji typu P. Zauważ, że chwilami s(t) jest ujemne. Czyli chłodzi. Po to, żeby szybciej osiągnąć stan ustalony.
Nie ma zerowego uchybu e(t). Jedyne co mogę, to zwiększyć Kp regulatora, np. na Kp=100.
Rozdz. 23.4.4 Regulacja Kp=100

Rys. 23-11
Schemat blokowy zasłania trochę dolne sygnały e(t) i x(t) ale zobaczysz je na animacji.
Co prawda w stanie ustalonym y(t)=0.99*x(t), czyli y(t) jest prawie równe wartości zadanej x(t), ale kosztem większych przeregulowań y(t). Na Rys. 23-6, badaliśmy regulację typu P dla członu inercyjnego i Kp=100. Tu mogliśmy dowolnie zwiększać Kp i układ dochodził do stanu ustalonego szybko i bez przeregulowań. Przy dużych Kp uchyb ustalony e(t) był prawie zerowy. Przy członie dwuinercyjnym oraz Kp=100 nie jest już tak miło. Czas regulacji i oscylacje są nie do zaakceptowania.
Rozdz. 23.4.5 Podsumowanie obiektu dwuinercyjnego sterowanego przez regulator P
Jest trudniejszy do sterowania niż inercyjny. Można udowodnić np. z kryterium Hurwitza że zwiększanie parametru Kp nie spowoduje niestabilności. Także z Nyquista który „łazi” tylko po 2 ćwiartkach obiektu otwartego. Za to pojawią się oscylacje i dłuższy czas regulacji.

23.5 Regulator P z obiektem trójinercyjnym
23.5.1 Badanie obiektu trójinercyjnego w układzie otwartym

Rys. 23-12
Do obiektu dwuinercyjnego dodany został szeregowo człon inercyjny o stałej czasowej T=0.5 sek.
Przekonasz się, jak taka mała zmiana może narozrabiać w układzie ze sprzężeniem zwrotnym.
Rozdz. 23.5.2 Regulacja Kp=10
Układ różni się od Rys. 23-9 tylko dodatkowym członem jednoinercyjnym włączonym szeregowo.

Rys. 23-13
Gdybym zaproponował klientowi taką regulację, to poszczułby psami. Nie dość że duży uchyb e(t)=0.09, to jeszcze dynda po jednej minucie. Zwiększenie wzmocnienia na Kp=30 chyba nie poprawi sytuacji!
Rozdz. 23.5.3 Regulacja Kp=30

Rys. 23-14
Układ stał się niestabilny. Chociaż wzór na wzmocnienie układu zamkniętego w przypadku niestabilności jest trochę bez sensu, to nie tak zupełnie do końca. Tu Kz=0.97 oznacza, że w oscylacji pojawia się składowa stała 0.97. Zobaczmy jeszcze to, co ucina oscyloskop. Otrzymasz schemat dokładnie taki sam jak na Rys. 23-14. Tylko nastawy oscyloskopu są takie, aby był widoczny cały sygnał sterujący s(t)

Rys. 23-15
Skala oscyloskopu jest taka mała, że skok jednostkowy x(t) jest prawie niewidoczny, blisko osi czasu. Za to widać jak zaczyna się bujać y(t) a zwłaszcza dużo większe s(t).
Rozdz. 23.5.4 Podsumowanie obiektu trójinercyjnego sterowanego przez regulator P
Najtrudniejszy do sterowania . Charakterystyka amplitudowo-fazowa układu otwartego przechodzi przez 3 ćwiartki. Dlatego zgodnie z kryterium Nyquista układ zamknięty może (ale nie musi) być niestabilny.

Rozdz. 23.6 Jak Regulator typu P tłumi zakłócenia?
Rozdz. 23.6.1 Wstęp
Tłumienie zakłóceń do główna robota regulatora. Nie byłoby automatyki gdyby tego nie umiał.
Wcześniej badaliśmy odpowiedź na skok, który trwał 1 minutę. To się jeszcze da wytrzymać. Ale następne eksperymenty będą trwały 2 minuty. Najpierw pojawi się skok x(t) a potem w 70 sekundzie zakłócenie z(t) dodatnie albo ujemne. To tak jakbyś wsadził dodatkową grzałkę lub chłodnicę do cieczy. Automatyka powinna skompensować to zakłócenie. Czyli przy dodatkowej grzałce regulator powinien zmniejszyć dostarczaną moc, a przy chłodnicy zwiększyć.
W sumie doświadczenie będzie trwało 2 minuty. Nie jest to dużo, ale niektórych może denerwować.
Zbadamy regulację typu P z zakłóceniem dodatnim i ujemnym dla wcześniej poznanych obiektów:
– jednoinercyjnego
– dwuinercyjnego
– trójinercyjnego
Rozdz. 23.6.2 Zakłócenie dodatnie z obiektem jednoinercyjnym Kp=10
Zaczniemy od obiektu jednoinercyjnego z regulatorem Kp=10

Rys. 23-16
Zakłóceniem z(t) jest tu dodatkowe grzanie +0.2. Tak jakby się pojawiła dodatkowa grzałka, albo skoczyło napięcie na grzałce.
Do 70 sek. tak jak na Rys. 26-3. Na zakłócenie z(t)=+0.2 w 70 sek. regulator zareagował prawidłowo. Obniżył moc grzania na grzałce za regulatorem. Co prawda widać niewielki wpływ zakłócenia, ale został on 11-krotnie stłumiony. Całkowite tłumienie, jak się później przekonasz, zapewni nam tylko regulacja z całkowaniem uchybu e(t) czyli typu I, PI lub PID.
Porównaj ze sterowaniem ręcznym na Rys. 22-16 w rozdz.22. Podobne przebiegi? Tak, tylko stany przejściowe są duuuużoo lepsze! Ale przy sterowaniu ręcznym uchyb ustalony wydaje się trochę mniejszy. Dziwne trochę. Dlaczego? Bo podświadomie włączyłeś składową I czyli całkowanie. Na stały uchyb zareagowałeś stopniowym powolnym zmniejszaniem sygnału sterującego s(t). Całkowaniem w regulacji zajmiemy się później.
Rozdz. 23.6.3 Zakłócenie ujemne z obiektem jednoinercyjnym Kp=10

Rys. 23-17
Tu zakłócenie jest ujemne, z(t)=-0.2. Regulator zareagował prawidłowo tzn. dodatkowym grzaniem. Ale uchyb nie jest zerowy tu e=0.09. Można go zmniejszyć zwiększając wzmocnienie regulatora np. Kp=100. Sprawdźmy to.
Rozdz. 23.6.4 Zakłócenie dodatnie z obiektem inercyjnym Kp=100

Rys. 23-18
Oscyloskop obcina sygnał sterujący s(t) na poziomie +2. Ale zdajesz chyba sobie sprawę z tego, że na początku skoku x(t) sygnał sterujący s(t) osiąga wartość +100! Większe Kp spowodowało, że uchyb jest prawie zerowy a reakcja prawie natychmiastowa. Układ prawie nie reaguje na zakłócenia.
Rozdz. 23.6.5 Zakłócenie ujemne z obiektem inercyjnym Kp=100

Rys. 23-19
Regulator zareagował prawidłowo tzn. dodatkowym grzaniem.
Rozdz. 23.6.6 Zakłócenie dodatnie z obiektem dwuinercyjnym Kp=10

Rys. 23-20
Początek tzn. odpowiedź na skok x(t) jest oczywiście taki, jak na Rys. 23-9. Weź pod uwagę że inna skala czasu. Trochę za dużo oscylacji i długi czas regulacji. Parametr Kp=10 nie jest zbyt duży i dlatego uchyb ustalony jest spory. Już lepiej wygląda tłumienie zakłócenia. Oscylacje mniejsze i czas ustalenia krótszy. Często reakcja na zakłócenia jest ważniejsza niż dojście do wartości zadane x(t). Dlaczego? Bo tłumienia zakłóceń są ciągle, natomiast zmiany wartości zadanej x(t) są rzadsze. Mimo wszystko trudno taki układ zaprezentować klientowi. Trochę wstyd dużego uchybu ustalonego. Eksperyment jest przykładem na to, że odpowiedź na skok jest inna niż na zakłócenie! A to dlatego, że transmitancja zakłóceniowa Gzakl(s)=y(s)/z(s) jest inna niż transmitancja układu zamkniętego Gz(s)=y(s)/x(s). Często się o tym zapomina, badając odpowiedź na skok wartości zadanej x(t) a nie na zakłócenie z(t).
Rozdz. 23.6.7 Zakłócenie ujemne z obiektem dwuinercyjnym Kp=10
Zakłócenie ujemne, czyli chłodzenie, zamiast dodatniego grzania.

Rys. 23-21
Reakcja prawidłowa. Układ stara się skompensować chłodzenie dodatkowym grzaniem.
Rozdz. 23.6.8 Zakłócenie dodatnie z obiektem trójnercyjnym Kp=10

Rys. 23-22
Już przy tak niedużym wzmocnieniu Kp=10 są zbyt duże oscylacje i czas ustalenia sygnału y(t). Chociaż stłumiło zakłócenie “grzanie” z(t)=+0.2 obniżeniem sterowania s(t). Całe szczęście, że istnieje regulacja PD. O tym pogadamy w następnym rozdziale.
Rozdz. 23.6.9 Zakłócenie ujemne z obiektem trójinercyjnym Kp=10

Rys. 23-23
Bez komentarzy
Z Rys. 23-14 i 23-15 wynika, że dla Kp=30 system jest niestabilny. Dlatego nie będziemy testować reakcji na zakłócenie z(t) dla tego Kp

Rozdz. 23.7 Dlaczego układ zamknięty jest lepszy od otwartego?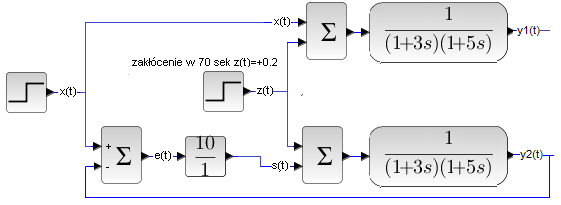

Rys. 23-24
Układ otwarty-górny i zamknięty-dolny na które działają sygnały:
– wejściowy x(t)
– zakłócenie z(t).
Problem dotyczy wszystkich regulatorów. Nie tylko P. Dla wielu jest to pytanie typu dlaczego lepiej być zdrowym i bogatym niż biednym i chorym?. Ja np. uważam, lepiej być zdrowym i bogatym.
Ale jeżeli masz nadal wątpliwości to porównaj jednoczesną odpowiedź układu otwartego y1(t) z odpowiedzią układu ze sprzężeniem zwrotnym y2(t) na sygnał wejściowy x(t) i zakłócenie z(t). Obiektem sterowanym i otwartym będzie wcześniej poznany człon dwuinercyjny. Regulator jest typu P, bo innego jeszcze nie znamy.

Rys. 23-25
Porównaj odpowiedź y1(t) układu otwartego i y2(t) zamkniętego. Do 70 sekundy niektórzy mogą się jeszcze zastanawiać, co się bardziej podoba. Sygnał „otwartego” y1(t) dochodzi do wartości x1(t)=1 trochę dłużej, za to bez oscylacji.
I najważniejsze
y1(t)=x(t)=1!
Czego nie można powiedzieć o y2(t), w którym uchyb to aż 9 %! Zdawałoby się, że jest 1:0 dla układu otwartego. Ale czar pryska w 70 sekundzie, gdy pojawia się ujemne zakłócenie z(t) (chłodzenie). „Otwarte” y1(t) spadło aż o 20% a „zamknięte” y2(t) tylko o 2%. W pierwszej chwili to wydaje się nawet, że y2(t) stoi jak drut.
Można jeszcze narzekać na 9% uchybu ustalonego układu zamkniętego. Na szczęście automatyka ma narzędzia do sprowadzenia go do zera. Zrobią to regulatory PI i PID w następnych rozdziałach.

Rozdz. 23.8 Podsumowanie regulacji typu P
Regulacja typu P
– Jest najprostszym regulatorem z grupy PID
– Przyspiesza przebieg sygnału wyjściowego i szybko tłumi zakłócenia.
– Nie zapewnia zerowego uchybu w stanie ustalonym. Tzn sygnał wyjściowy ustalony y(t) jest zawsze mniejszy od wartości zadanej x(t).
– Uchyb jest tym mniejszy im większe jest wzmocnienie regulatora Kp
– Dla członów jednoinercyjnych wzmocnienie Kp może być bardzo duże. Możemy wtedy przyjąć że uchyb jest zerowy, a odpowiedź y(t) jest natychmiastowa. Takie podejście jest też możliwe dla członów wieloinercyjnych, gdy pozostałe stałe czasowe T1, T2,…Tn są dużo mniejsze od podstawowej stałej czasowej T1. Wtedy traktujemy go „prawie” jako jednoinercyjny. Niestabilność może wystąpić, ale dopiero przy bardzo dużych Kp.
Wadą regulacji typu P jest to, że wymaga większego Kp niż PI lub PID. A to nie tylko oscylacje i ewentualna niestabilność. Duże Kp powoduje, że na samym początku sygnał sterujący s(t) jest np 10 razy większy niż potrzeba, żeby sygnał wyjściowy y(t) doszedł do wartości zbliżonej do wartości zadanej x(t). W przypadku podgrzewania wody oznacza to, że moc grzałki jest też 10 razy większa niż w stanie ustalonym. Także kable powinny być większe.
Dotąd zakladaliśmy, że nie występują żadne ograniczenia mocy. W praktyce zawsze jakieś wystąpią, choćby od napięcia zasilania. Spowoduje to wolniejszy przebieg niż idealny. Do tematu wrócimy jeszcze w rozdziale 30.
Generalnie to w regulacji P ( i nie tylko) jest podstawowa sprzeczność celów. Duże Kp to mały uchyb regulacji –super, ale także oscylacje i nawet niestabilność. W następnym rozdziale dowiesz się, że dodanie do regulatora P składowej różniczkującej D działa jak balsam. „Uspokaja” i pozwala dać większe Kp–>mniejszy uchyb regulacji, chociaż w dalszym ciągu nie zapewnia zerowego uchybu e(t). Mamy wtedy do czynienia z regulacją typu PD.