Podstawy automatyki
Rozdz. 9 Człon różniczkujący z inercją
Rozdz. 9.1 Wstęp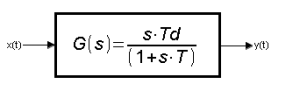
Rys. 9-1
Transmitancja członu różniczkującego z inercją.
Pamiętasz idealny człon różniczkujący? Narastający liniowo sygnał x(t) na wejściu, wywoływał skok y(t) na wyjściu o amplitudzie proporcjonalnej do prędkości narastania x(t). Podobnie działa różniczkujący z inercją. Też mierzy prędkość narastania x(t), ale robi to z pewną inercją. Można powiedzieć, że obliczanie prędkości narastania x(t), czyli obliczanie pochodnej y(t)=x'(t) zajmie mu trochę czasu. Nie tak natychmiast jak w idealnym
Rozdz. 9.2 Człon różniczkujący Td=2sek z inercją T=0.5 sek , piła z oscyloskopem
Rys. 9-2
Człon różniczkujący Td=2 sek inercją T=0.5 sek
.Do badania różniczkującego z inercją najlepiej nadaje się x(t) narastające liniowo z prędkością (pochodną!) 1/sek. Czyli piła. Wzór na x(t) podany jest na wykresie. Sprawdź czy się zgadza np. dla t=0 i t=7 sek. Sygnał wyjściowy obliczający prędkość x(t) ustalił się po ok. pięciu stałych czasowych T, czyli po 5*0.5 =2.5 sek. Czyli T świadczy o jakości tego prędkościomierza.
Tani prędkościomierz poda dokładną prędkość np. po 2.5 sek tak jak w przykładzie, a dobry po np. 0.5 sek.
A co to jest Td=2 sek? Wróć na chwilę do idealnego członu różniczkującego–>rozdz. 9, czyli bez inercji. Tam Td=1 sek i był to czas po którym wyjście y(t) zrównało się z piłą x(t). Tu definicja jest podobna, tylko dotyczy stanu ustalonego np. po 3 sek. Tu po Td=2 sek przyrost sygnału x(t) też równa się y(t)=2. Zauważ, że większe Td to większa intensywność różniczkowania.
Rozdz. 9.3 Człon różniczkujący z inercją Td=2, T=0.5 sek , impuls prostokątny z oscyloskopem
Rys. 9-3
Zamiast piły na wejściu jest impuls prostokątny
Porównaj ten przebieg z analogicznym, tylko dla idealnego członu różniczkującego –>Rys. 5-9 rozdz. 5. Tam przy dodatnim zboczu skoku x(t) prędkość y(t) była nieskończenie duża. Idealny pokazał to dobrze jako impuls Diraca. Tu natomiast rzeczywisty pokazał y(t) jako prędkość 4/1sek gdy t=3.5sek.
Z wykresu y(t) można otrzymać parametry członu różniczkującego:
– T=3.5-3=0.5sek (z zielonej stycznej)
– Td=4/05sek=2/sek
