Liczby zespolone
Rozdział 3 Funkcje zespolone
Rozdział 3.1 Wstęp
Umiesz już dodawać, odejmować, mnożyć i dzielić liczby zespolone. Przyszedł czas na funkcje.
W elektrotechnice, automatyce i temu podobnych stosuje się głównie funkcję zespoloną:
-wymierną
-wykładniczą o podstawie e
Pozostałe funkcje zespolone np. trygonometryczne, logarytmiczne używamy rzadziej i nie będziemy się nimi zajmować.
Wykresy funkcji zespolonych są bardziej skomplikowane niż funkcji rzeczywistych. Każdemu punktowi dwuwymiarowemu na płaszczyźnie z przyporządkowujemy liczbę zespoloną f(z), która też jest punktem dwuwymiarowym, Wchodzimy więc w przestrzeń czterowymiarową! Trudną do wyobrażenia dla zwykłego zjadacza chleba.
Rozdział 3.2 Funkcja zespolona wymierna
Obliczymy ją wykorzystując tylko dodawanie, odejmowanie, mnożenie i dzielenie.
Dowolną potęgę z otrzymamy poprzez kolejne mnożenia.
Dowolny wielomian z, czyli “sumę potęg” poprzez potęgowanie, dodawanie i odejmowanie
Dowolną funkcję wymierną czyli iloraz wielomianów, poprzez potęgowanie, dodawanie, odejmowanie i dzielenie
Rys. 3-1
Zespolone funkcje wymierne
Rozdział 3.3 Zespolona funkcja wykładnicza exp(z)
Rozdział 3.3.1 Definicja
Ściślej-wykładnicza o podstawie e, inaczej eksponencjalna.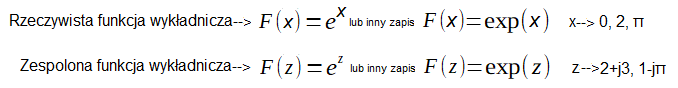
Rys. 3-2
Funkcja zespolona exp(z) o podstawie e czyli funkcja wykładnicza inaczej eksponencjalna
Rozdział 3.3.2 Liczba e=2,7182818…
Niewymierna liczba rzeczywista e=2,71828… jest czwartą którą wypada znać po 0,1 i π. Skąd się wzięło 0 i 1 to każdy wie*. Liczba π=3,14… to połowa obwodu do promienia. Ale liczba e? Czy jest dla niej jakaś prosta interpretacja typu “obwód do promienia”. Jest, ale mniej oczywista i w dodatku przyszła ze świata bankowego
*A właściwie to skąd?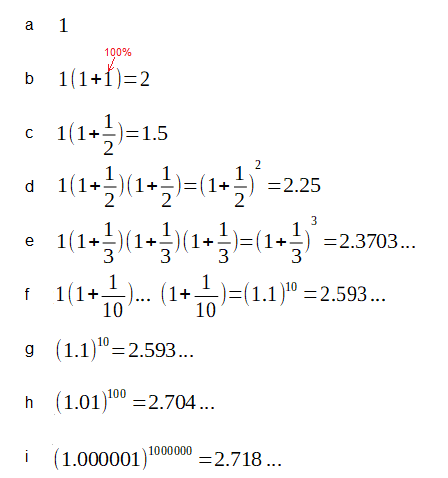
Rys. 3-3
Liczba e a odsetki w banku.
a Włożyłem złotówkę do banku z odsetkami 100% po roku. Swoją drogą niezłe odsetki i bank jest super.
b Po roku powinno być 2 zł. Zwróć uwagę na to że 1 to 100%
c Umówiłem się z bankiem, że odsetki też będą 100% ale kasę 1.5zł odbiorę po pół roku. Po bankowemu- kapitalizacja po pół roku
d Gdybym odebrał po roku tj. po 2 kapitalizacjach to byłoby 2.25zł
e A gdyby były 3 kapitalizacje to po roku 2.3703…zł
f 2.593…zł po roku po 10 kapitalizacjach
g To samo tylko inny zapis
h 2.704…zł po roku po 100 kapitalizacjach
j 2.718….zł po roku po 1000000 kapitalizacjach
Im więcej kapitalizacji w roku tym bardziej zbliżamy się do tzw. kapitalizacji ciągłej. Wtedy po roku z 1 zł zrobi się e=2,7182818…zł.
Obliczenia łatwo sprawdzisz kalkulatorem.
Wniosek:
Liczbą e jest kapitalizacją ciągłą z 1 zł po 1 roku przy odsetkach 100%.
Rozdział 3.3.3 Rzeczywista funkcja wykładnicza exp(x)
Zanim przystąpimy do wersji zespolonej zajmiemy się wersją rzeczywistą. Czyli funkcją wykładniczą o podstawie e. Bez problemu obliczymy metodą mnożenia wartości tych funkcji dla wykładnika całkowitego 0,1,2,3…![]()
Rys. 3-4
Wartości funkcji wykładniczej dla wartości całkowitych
Ale ale jak ją policzyć dla np. dla x=1.234?
Zrobimy to co robią wszystkie kalkulatory. Tzn. rozłożymy funkcję na szereg potęgowy np. szereg Maclaurina.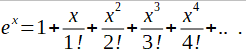
Rys. 3-5
Funkcja wykładnicza jako szereg potęgowy
W ten sposób obliczymy wartość funkcji dla dowolnego x korzystając tylko z 4 podstawowych operacji matematycznych.
Uwaga:
Symbol ! to tzw. silnia
Np. 3!=1*2*3=6
Rozdział 3.3.4 Zespolona funkcja wykładnicza exp(z)
Umiemy już obliczyć wartość funkcji wykładniczej exp(x) dla dowolnego x rzeczywistego. Zróbmy to samo, ale dla dowolnej liczby zespolonej z. Ciekawe jak ten twór będzie się zachowywał? Może gryzie, może kopie?
Rozłóżmy więc exp(z) na zespolony szereg potęgowy Maclaurina.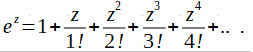
Rys. 3-6
Funkcja wykładnicza (eksponencjalna) jako zespolony potęgowy Maclaurina.
Rozdział 3.3.5 Szczególny przypadek exp(z) czyli exp(jωt)
Rys. 3-6 może być definicją zespolonej funkcji wykładniczej! Bez problemu obliczymy jej wartość dla dowolnego z przy pomocy tylko 4 podstawowych działań, które już znamy. Bez problemu, ale dość żmudnie, bo z jest parą liczb! Także wykres exp(z) jest trudny do wyobrażenia–>patrz p. 3.1. Dlatego zajmiemy się jej szczególnym przypadkiem, gdy z=jωt dla t=0…∞ Czyli gdy dziedziną jest górna połówka osi urojonej Im z. Rozpatrzymy więc funkcję zespoloną exp(jωt), która jak się później okaże, idealnie nadaje się do analizy przebiegów sinusoidalnych. A to jest przecież podstawą takich dziedzin jak elektrotechnika, automatyka, radiotechnika, akustyka…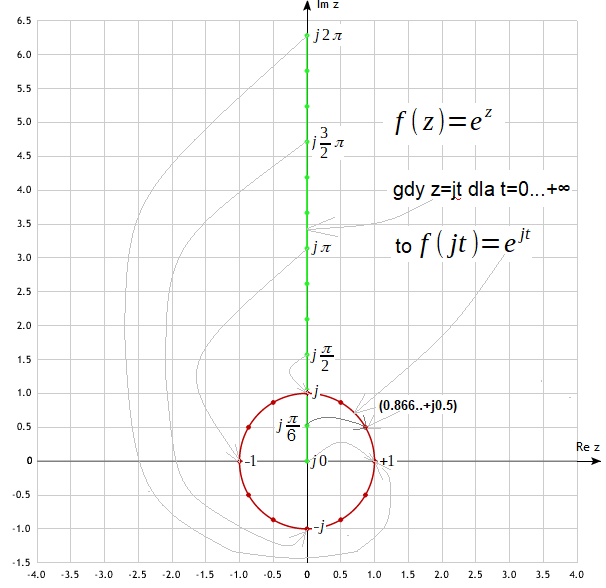
Rys. 3-7
Funkcja wykładnicza exp(z) dla z=jt czyli dla z=jωt gdy ω=1/sek jest tzw. pulsacją.
Dziedziną exp(z) są punkty 0…∞ górnej zielonej półosi urojonej Im z. Wartością funkcji są punkty na czerwonym okręgu. Wyznaczono je podstawiając do wzoru z Rys. 3-6 kolejne liczby- zielone punkty
półosi Im z tj. j0, jπ/6, jπ/2, j3π/2 i j2π. Przyporządkowano nim odpowiednie czerwone punktyexp(jt) na okręgu tj.+1, (0.866..+j0.5),+j, -1 i -j. Są też inne, ale nie opisane, pośrednie zielone punkty na półosi urojonej Im z. Dla nich też są przyporządkowane odpowiednie czerwone punkty na okręgu.
Ze wzoru z Rys. 3-6 wynika np. że dla:
exp(j0)=+1
exp(jπ/6)=0.866..+j0.5
exp(jπ/2)=+j
exp(jπ)=-1
exp(j3π/2)=-j
exp(j2π)=+1
Okrąg jest wykresem exp(jt) dla jt=0…∞. Ale zbadaliśmy tylko zakres jt=0…2π, dla którego obraz exp(jt) wykonał pełen obrót. Okaże się i można to sprawdzić, że drugi taki sam obrót będzie wykonany dla t=2π…4π, trzeci dla t=4π…6π itd…Jest to więc funkcja okresowa!
Byliśmy ciekawi jak ten twór exp(z) będzie się zachowywał? I kto by się tego spodziewał, że zespolona funkcja wykładnicza może być funkcją okresową. Ona gryzie i kopie!
Rozdział 3.3.6 Jak powstał okrąg na Rys 3-7?
Czyli jak obliczyliśmy wartości funkcji zespolonej exp(jt) dla jt=0…∞?
Nie możemy przecież stosować wzoru Eulera:
exp(jt)=cos(t)+jsin(t)
bo go jeszcze nie znamy.
exp(j0)
Pierwsza wartość exp(j0)= exp(0)=+1 jest banalna, bo j0=0 to liczba rzeczywista.
exp(jπ/6)
Dla jπ/6 już nie jest tak miło. Skorzystamy więc ze wzoru Rys. 3-6. Tu są tylko 4 podstawowe działania matematyczne, ale robota męcząca. Dlatego polecam wszystkim genialne narzędzie matematyczne program Wolfram Alfa*
Wywołaj www.wolframalpha.com i zrób co każe rysunek. Pamiętaj tylko, że dla WolframAlfa liczbą urojoną jest i a nie “elektryczne” j.
Po wpisaniu do okna dialogowego pierwszych 6 składników z szeregu Maclaurina Rys. 3-6 i kliknięciu odpowiedniego klawisza program policzy przybliżenie exp(jπ/6).
Uwaga:
Rys. 3-8 trochę różni się od tego co pokazał WolframAlfa, ale treść jest ta sama. Po prostu poprzesuwałem różne elementy tak aby rysunek był bardziej zwarty. Dotyczy to też następnych wywołań WolframAlfa.
*O samym programie WolframAlfa napisałem więcej w kursie Szeregi Fouriera Wirująco w rozdz. 11.2..
Rys. 3-8
exp(jπ/6) jako 6 pierwszych składników szeregu Maclaurina z Rys. 3-6
Zauważ, że przybliżoną wartość exp(jπ/6)≈0.866…+j0.5… program policzył wykorzystując tylko 6 pierwszych wyrazów szeregu potęgowego. Ale zrobił to dość przyzwoicie. Dla postronnego obserwatora wynik leczy prawie dokładnie na okręgu o promieniu r=1 pod kątem π/6=30°. podczas gdy obliczone dane to r=1.00003 oraz θ=29.9993° jako Polar coordinates. Obliczone exp(jπ/6) zostały też pokazane na płaszczyźnie zespolonej jako Position in the complex plane. Niezły jest ten Wolframik!
Pozostałe exp(jt) dla jπ/2, j3π/2 i j2π też obliczymy wolframem, ale już wyspecjalizowaną funkcją zespoloną exp(z).
Czym exp(z) różni się od szeregu Maclaurina z Rys. 3-6?
Myślę, że dwoma rzeczami:
-Więcej składników niż 6. Ile dokładnie? Nie wiem.
-Założeniem, że funkcja jest okresowa.
A więc liczmy.
exp(jπ/2)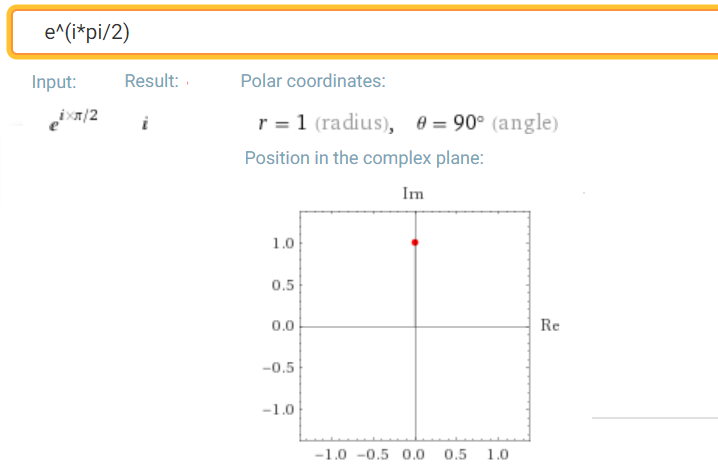
Rys. 3-9
exp(jπ/2)
Jak idealnie to policzył!
exp(jπ)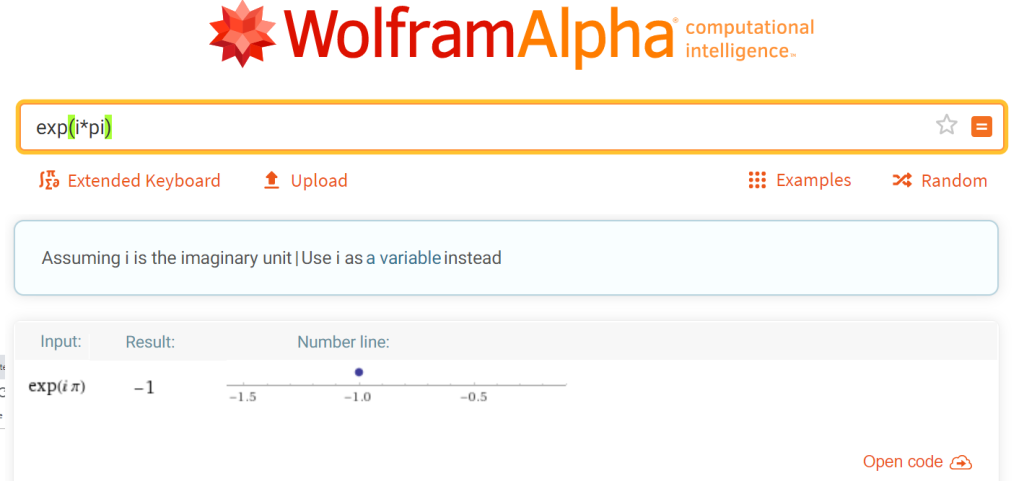
Rys. 3-10
exp(jπ)=-1
Podobno wyrażenie
exp(jπ)=-1 albo inaczej exp(jπ)+1=0
jest najpiękniejszym równaniem matematyki.
Dlaczego? Bo są w nim charakterystyczne 4 liczby 0,1,e,π oraz jedna liczba urojona j.
exp(j3π/2)
Rys. 3-11
exp(j3π/4)
exp(j2π)
Rys. 3-12
exp(j2π)
Zauważ, że exp(j2π)= exp(j0)=+1
Rozdział 3.7 Wzór Eulera
Powracając do wspomnianego wcześniej wzoru Eulera
exp(jt)=cos(t)+jsin(t)
lub bardziej ogólnie
exp(jωt)=cos(ωt)+jsin(ωt)
gdzie ω jest tzw. prędkością kątową w radian/sek, to bardziej jest znany w “wersji kątowej” gdzie zamiast ωt jest kąt α
exp(jα)=cos(α)+jsin(jα)
Wzór znany jest już od XVIII wieku i ma bardzo łatwą interpretację graficzną
Rys. 3-13
z=exp(jα)=cos(α)+jsin(jα)
Sprawdź ten wzór dla np. dla α=0, π/6, π/2, π,3π/2 i 2π a otrzymasz wyniki które wyznaczałeś Wolframem w Rozdziale 3.3.5.
Np. exp(jπ/6)=0.866..+j0.5
