Podstawy automatyki
Rozdz. 26.1 Wstęp
Rozdz. 26.1
Z p. 25.8 poprzedniego rozdziału dowiedzieliśmy się że:
– Regulacja typu P a tym bardziej PD szybko reaguje na wartość zadaną x(t), ale nie zapewnia zerowego uchybu ustalonego e(t)=0.
– Z regulacją typu I jest odwrotnie. Układ wolno dochodzi do wartości ustalonej , za to zapewnia zerowy uchyb ustalony e(t)=0.
Dlatego idea regulatora PI z torem proporcjonalnym P i całkującym I narzuca się sama. Spodziewamy się, że jego reakcja na skok x(t) i zakłócenie z(t) będzie szybsza niż regulatora I (choć nie tak szybka jak P lub PD!), za to w stanie ustalonym uchyb e(t) będzie zerowy. Zaczniemy od badania struktury PI. Nie jest to jeszcze regulator PI tylko człon PI, ponieważ wejściem jest tylko pojedynczy sygnał x(t) a nie uchyb e(t)=x(t)-y(t).
Rozdz. 26.2 Człon PI
Rozdz. 26.2.1 Człon PI Kp=1 Ti= 1 sek
Rys. 26-1
Kp=1 Ti=1 sek
Sygnałem wejściowym jest skok jednostkowy x(t). Wyraźnie widać składową proporcjonalną yp(t) i całkującą yi(t). Składowa yp(t) jest dla Kp=1 powtórzeniem skoku x(t). Składowa yi(t) jest narastającą “pilą”, dla której wartość po czasie Ti=1sek też jest yi(t)=1. Sygnał regulatora y(t) jest wtedy podwojoną wartością sygnału początkowego y(t). Stąd inną nazwą czasu całkowania Ti jest czas zdwojenia Ti. Przy tym samym Ti i różnych Kp regulatora PI, prędkości narastania sygnału wyjściowego y(t) są różne, ale ich parametry Ti będą oczywiście jednakowe.
Rozdz. 26.2.2 Człon PI Kp=1 Ti= 10 sek
Rys.26-2
Kp=1 Ti=10 sek.
Całkuje 10 razy wolniej niż poprzednio, ale po czasie Ti=10 sek sygnał wyjściowy też został podwojony.
Rozdz. 26.2.3 Człon PI Kp=3 Ti= 10 sek
Rys. 26-3
Całkuje 3 razy szybciej niż poprzednio, ale po czasie Ti=10 sek sygnał wyjściowy też został podwojony.
Czyli nastawa Kp nie ma wpływu na Ti.
Rozdz. 26.3 Układ Regulacji z dydaktycznym regulatorem PI
Rozdz. 26.3.1 Dydaktyczny regulator PI
Dydaktyczny Regulator PI który zmajstrowałem wykaże że składowa:
– proporcjonalna P zapewnia szybsze działanie
– całkująca I zapewnia zerowy uchyb
– przy skoku jednostkowym x(t) zaczyna jako proporcjonalny P a kończy jako całkujący I. Przemiana ta wystąpi w pewnym momencie. W prawdziwym regulatorze PI przemiana P–>I występuje w sposób ciągły. Przekonasz się o tym później.
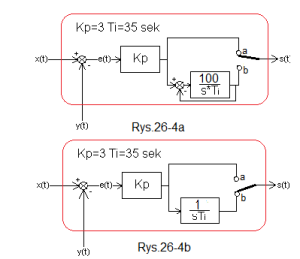
Rys. 26-4
Struktura regulatora zależy od położenia styku:
– Rys. 26-4a – styk “góra”
Struktura typu P. Zauważ, że w tym czasie na styku b, dzięki silnemu ujemnemu sprzężeniu zwrotnemu obejmującemu człon całkujący, napięcie napięcie na styku b śledzi napięcie na styku a. Ściślej ze stukrotnie zmniejszoną stałą czasową T=Ti/100, czyli prawie bez opóźnień. Jak nie wierzysz to podstaw G(s)=100/sTi do najważniejszego wzoru w automatyce–> Rys. 15-3d rozdz. 15.
– Rys. 26-4b – styk “dół”
– struktura typu I. Dzięki w.w śledzeniu po przełączeniu ze styku a na b układ będzie się zachowywać tak jak na animacji na Rys. 26-5.
Rys. 26-5
Do 25 sekundy regulator jest typu P i y(t)=Kp*e(t)=3*1=3. W 25 sekundzie styki opadają (widać to na animacji) i regulator staje się typu I. Dzięki “śledzeniu”–>Rys. 26-4a ,całkowanie rozpoczyna się od poziomu +3V a nie od OV. Po tzw. czasie zdwojenia Ti=25 sek składowa I zrównała się ze składową P. Gdyby np. w 40 sek. uchyb e(t) wzrósł trochę skokowo, to s(t) zacząłby narastać tak jak linia przerywana. Nie będzie żadnego skoku sygnału s(t), bo działa tylko składowa całkująca I.
Rozdz. 26.3.2 Układ regulacji z dydaktycznym regulatorem PI
Wykażemy że składowa:
-proporcjonalna P odpowiada za szybkie dojście y(t) do stanu bliskiemu wartości zadanej x(t),
-całkująca I odpowiada za dojście do stanu w którym y(t)=x(t). Czyli zapewni zerowy uchyb ustalony e(t).
Potem łatwiej zrozumiesz działanie prawdziwego regulatora PI.
Rys. 26-6
Zastosowano regulator dydaktyczny PI z nastawami Kp=10 i Ti=50 sek.
Przed 12 sek działa tylko składowa proporcjonalna P, zaś po 12 sek całkująca I.
Zanim wciśniesz przycisk video, przyjrzyj się dokładnie sygnałom:
– sterujący niebieski s(t)
– wyjściowy czerwony y(t)
– uchyb zielony e(t)
W 12 sek nastąpiła zmiana struktury regulatora z P na I, czyli opadnięcie styków z a na b.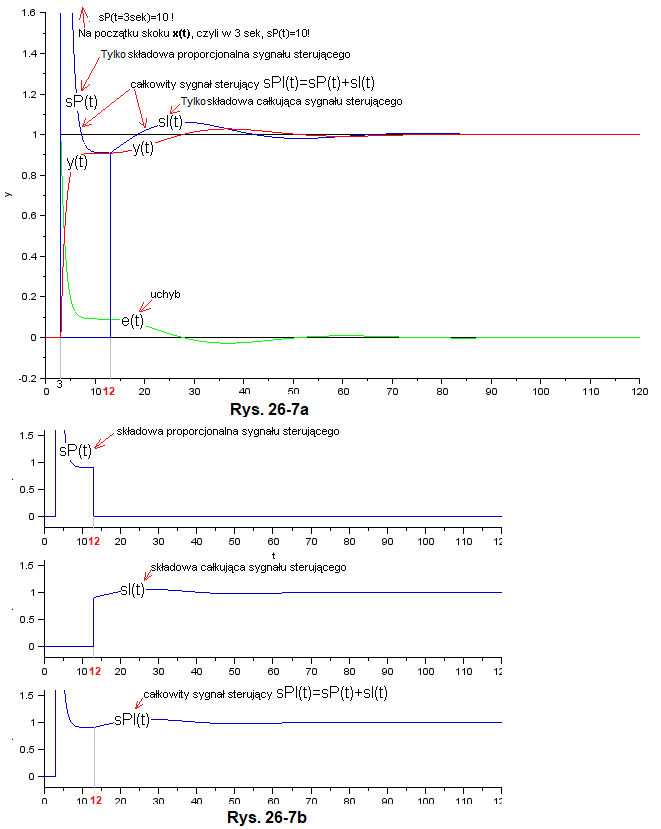
Rys. 26-7
Rys. 26-7a przedstawia wszystkie przebiegi czasowe na jednym wykresie. Sygnały sterujące sP(t), sI(t) i sPI(t) nakładają się na siebie i dlatego powstał Rys. 26-7b, na którym te sygnały pokazane są z osobna.
Tu wyraźnie widać, że w 13 sek znika składowa proporcjonalna sP(t) i pojawia się składowa całkująca sI(t). Sygnał całkowity sPI(t) jest sumą składowych sP(t) i sI(t). Ze względu na różne skale przebiegi na Rys. 26-12a i Rys. 26-12b nie są identyczne..
W 3 sek wystąpił skok jednostkowy x(t). Wtedy sygnałem sterującym jest tylko składowa proporcjonalna sP(t) i sygnał wyjściowy y(t) bardzo szybko dojdzie do stanu ustalonego y=0.91. Na pewno szybciej niż gdyby działał tylko regulator I.
W 12 sek regulator zmienia swój charakter z P na I i od tego czasu działa tylko składowa całkująca sI(t). Dobrze wiemy, że potrafi ona sprowadzić uchyb e(t) do 0, co zresztą ochoczo czyni. Dlatego po ok. 90 sek x(t)=y(t)=1 czyli e(t)=0.
Krótko i na temat.
W regulacji typu PI składowa P doprowadza szybko sygnał wyjściowy y(t) do sygnału bliskiego wartości zadanej x(t) (ale mniejszego) tu do y(t)=0.91. Regulacja typu P nie jest w stanie doprowadzić sygnału ustalonego y(t) do wartości y(t)=x(t).
Regulator dydaktyczny zna tą ułomność i dlatego w 12 sek wyłącza sP(t) i włącza sI(t). A składowa całkująca sI(t) doprowadzi po pewnym czasie sygnał y(t) do wartości y(t)=x(t)=1, czyli zapewni zerowy uchyb regulacji.
Rozdz. 26.3.3 Porównanie dydaktycznego PI z regulacją typu P
Spójrz na Rys. 26-7a. Regulator typu P jest szczególnym przypadkiem regulatora dydaktycznego, w którym nigdy nie nastąpi przełączenie z P na I. Czyli po 12 sek. pozostanie ten sam stan y=0.91. W porównaniu do regulatora dydaktycznego PI uchyb regulacji typu P nie jest zerowy.
Rozdz. 26.3.4 Porównanie dydaktycznego PI z regulacją typu I
Regulator całkujący typu I jest optymalny dla obiektu jednoinercyjnego o stałej czasowej T=10 sek, gdy jego nastawa Ti=16 sek. Porównajmy tą regulację z dydaktycznym PI.
Rys. 26-8
Na 2 układy regulacji z obiektem inercyjnym sterowane przez regulator:
-dydaktyczny PI
– klasyczny I (całkujący)
podawany jest ten sam skok jednostkowy x(t). Obydwa regulatory powinny sprowadzić uchyb ustalony e(t) do O. Który zrobi to lepiej? Tzn. szybciej i z mniejszymi oscylacjami.
5:0 dla dydaktycznego PI. Dochodzi on do stanu ustalonego y(t)=1 szybciej i z mniejszymi oscylacjami niż regulacja typu I. Wkrótce przekonasz się, że prawdziwa regulacja PI jest jeszcze lepsza!
Rozdz. 26.4. Regulator PI z obiektem jednoinercyjnym
26.4.1 Wstęp
Czas na “prawdziwy” regulator PI , czyli po prostu regulator PI.
Ten temat p.26.4 oraz p.26.5 i p.26.6
to regulatory PI sterujące obiektami:
– jednoinercyjnym,
-dwuinercyjnym,
-trójinercyjnym.
Będziemy badać układy regulacji przy różnych nastawach Kp i Ti. Zawsze zaczniemy od wyłączonej akcji całkowania i wtedy z regulatora PI “zrobi” się regulator P. Po co ta szopka? Bo zobaczysz główną zaletę regulatora PI. Sprowadzanie uchybu regulacji do O przy dużo szybszym działaniu niż robi to regulator I.
Rozdz. 26.4.2 Obiekt jednoinecyjny
Rys. 26-9
Obiekt inercyjny o stałej czasowej T=10 sek K=1
Przy okazji przypomnisz sobie jak odczytać z wykresu parametry obiektu jednoinercyjnego K=1 i T=10 sek.
Rozdz. 29.4.3 Regulacja PI Kp=3 wyłączone całkowanie
Czyli mamy typową regulację typu P. Kp=3 wyłączone całkowanie (0 w liczniku członu całkującego I wyłącza całkowanie).
Rys. 26-10
Do ok. 19 sek regulacja działa tak jak regulacja dydaktyczna PI do 12 sek na Rys. 26-6. Czyli jest to regulacja typu P. Co prawda na Rys. 26-6 jest inne Kp, ale nie przeszkadza nam to w analizie. Sygnał wyjściowy osiągnął po 19 sek. stan ustalony y(t)=0.75 i jest to zgodne z wykresem i z teorią dla regulacji typu P. Powstał więc niezerowy uchyb e(t)=0.25. Aby zlikwidować niezerowość uchybu e(t), wprowadźmy do boju składową całkującą I. Zaczniemy od ostrożnego (“wolnego”) całkowania Ti=12 sek.
Rozdz. 26.4.4 Regulacja PI Kp=3 Ti=12 sek
Gdybyś chciał sobie przypomnieć jak człon PI reaguje na skok x(t) w układzie otwartym to wróć do rozdz. 26.2.
Po dodaniu składowej I regulator P stał się regulatorem PI. Czy uchyb ustalony e(t) będzie wyzerowany?
Rys. 26-11
Yes, yes, yes!!! Po ok. 50 sekundach) czerwone y(t) pokryło się z czarnym x(t). Czyli uchyb e(t)=0 został wyzerowany. Taki całkiem niezły przebieg został uzyskany przy dość ostrożnych nastawach, małym Kp i dużym Ti. Spodziewamy się, że przy bardziej “agresywnych” nastawach układ szybciej dojdzie do stanu ustalonego y(t)=1. Być może kosztem oscylacji, bo nic w życiu nie jest za darmo.
Rozdz. 26.4.5 Dokładniejsza analiza Regulacji PI Kp=3 Ti=12 sek
Spróbujmy znaleźć analogię z dobrze już rozpracowanym regulatorem dydaktycznym PI, czyli z przebiegiem na Rys. 26-6. Ten sam układ regulacji co poprzednio. Ale teraz badamy nie tylko sygnał sterujący regulatora sPI(t) lecz także jego składową proporcjonalną sP(t) i całkującą sI(t).
Rys. 26-12
Dydaktyczny regulator PI z Rys. 26-6, rozpoczyna akcję jako (tylko) proporcjonalny P. Dzięki temu bardzo szybko dochodzi do stanu ustalonego. Przypomnę, że w regulacji P na początku skoku sygnał sterujący jest bardzo duży i to właśnie wymusza szybki przebieg. Potem gdy został już osiągnięty stan ustalony (który zawsze jest mniejszy od x(t)=1) następuje przełączenie na akcję całkowania I. Teraz regulator całkujący I zrobi to co umie najlepiej. Dokończy akcję czyli sprowadzi uchyb regulacji do 0. Czerwone y(t) pokryje się z czarnym x(t).
A jak to robi “prawdziwy” regulator PI na Rys. 26-12?
Podobnie. Na początku skoku x(t) działa tylko składowa proporcjonalna sP(3)=3, ponieważ całkująca sI(t) “nie zdążyła jeszcze urosnąć” (sI(3)=0). Tak jak w dydaktycznym.
A w stanie ustalonym np. w 55 sekundzie?
Tu jest odwrotnie, działa tylko składowa całkująca sI(t) bo proporcjonalna znikła- sP(55)=0. Też tak jak w dydaktycznym.
A pomiędzy t=3 sek i t=55 sek?
Wtedy zanika sP(t) a rośnie sI(t). Czyli używając słów eleganckich regulator P “przepoczwarza” się w regulator I. W sposób ciągły a nie skokowy jak regulator dydaktyczny PI! To tyle. Są pytania? Nie widzę. To zróbmy bardzie agresywne (inaczej-szybsze) całkowanie. Mam nadzieję, że przyspieszy to przebieg bez przesadnych oscylacji.
Rozdz. 26.4.6 Regulacja PI Kp=3 Ti=4 sek
Bardziej agresywne całkowanie na pewno przyspieszy przebieg, ale czy kosztem dużych oscylacji?
Rys. 26-13
Od tej pory zmienił się zakres oscyloskopu. Było 0…3, jest -1…2. Skala pozostała taka sama. Zmiana ze względu pojawienie się ujemnego e(t).
Szybszy przebiegi w porównaniu do Rys. 26-12 gdy Ti=12sek. Stan ustalony jest już po ok. 25 sek. kosztem pewnego przeregulowania. Niektórym bardziej może podobać się poprzednie Ti=4 sek. Ale załóżmy, że dla naszego Klienta priorytetem był czas dojścia do stanu ustalonego. Nawet kosztem pojawienia oscylacji. A może damy jeszcze szybsze całkowanie?
Rozdz. 26.4.7 Regulacja PI Kp=3 Ti=2 sek
Rys. 26-14
Chyba przesadziliśmy. Duża oscylacja a czas regulacji podobny do poprzedniego.
Do tej pory badaliśmy układ zmieniając Ti gdy Kp=3. Dalej będziemy robić to samo, ale przy Kp=10. Spodziewamy się szybszych przebiegów i większych oscylacji.
Rozdz. 26.4.8 Regulacja PI Kp=10 bez całkowania
Zaczniemy od regulacji bez całkowania. czyli od regulacji typu P.
Rys. 26-15
Z wykresu i teorii dla regulacji proporcjonalnej dla Kp=10 sygnał wyjściowy y(t) w stanie ustalonym wynosi y=0.91 a uchyb e=0.09.
Na Rys. 26-16 jest ten sam przebieg, ale w innej skali. Zobaczysz cały “nieobcięty” sygnał sterujący s(t).
Rys. 26-16
Kurczę, duży jest ten sygnał sterujący s(t).
Rys. 26-17
Lepiej niż Kp=3 i Ti=4sek na Rys. 26-13. To zwiększmy jeszcze intensywność całkowania.
Rozdz. 26.4.10 Regulacja PI Kp=10 Ti=5 sek
Rys. 26-18
Chyba lepiej. Jest co prawda niewielkie przeregulowanie, ale stan ustalony nastąpił znacznie szybciej.
Po 20 sekundzie. Znowu zwiększymy całkowanie.
Rozdz. 26.4.11 Regulacja PI Kp=10 Ti=1.75 sek
Rys. 26-19
Jeżeli zależy nam na czasie regulacji i nie przeszkadza przeregulowanie ok. 20% to nastawy Kp=10 Ti=1.75sek są najlepsze dla naszego obiektu jednoinercyjnego. W przeciwnym wypadku Kp=10 Ti=5sek są optymalne. Oczywiście mogą być jeszcze lepsze nastawy. Należy tylko zbadać odpowiedzi przy innych kombinacjach Kp i Ti.
Przejdźmy teraz do szukania optymalnej nastawy dla obiektu nieco trudniejszego do sterowania- Dwuinercyjnego.
Rozdz. 26.5 Regulator PI z obiektem dwuinercyjnym
26.5.1 Obiekt dwuinecyjny
Rys. 26-20
Obiekt dwuinercyjny o stałych czasowych T1=3 sek, T1=5 sek, K=1. Widzisz typowy dla członów wieloinercyjnych punkt przegięcia.
Rozdz. 26.5.2 Regulacja PI Kp=3 wyłączone całkowanie
Zaczynamy więc od regulacji P.
Rys. 26-21
Sygnał wyjściowy osiągnął po 35 sek. stan ustalony y(t)=0.75 i jest to zgodne z wykresem i z teorią dla regulacji typu P. Powstał niezerowy uchyb e(t)=0.25. Aby uchyb e(t) był zerowy, wprowadźmy składową całkującą I. Zaczniemy ostrożnie od Ti=32 sek.
Rozdz. 26.5.3 Regulacja PI Kp=3 Ti=32 sek
Rys. 26-22
Sygnał uchybu e(t) dochodzi do stanu zerowego, Nie zdążył dojść bo za krótki czas eksperymentu.
Rozdz. 26.5.4 Regulacja PI Kp=3 Ti=8 sek
Rys. 26-23
Tu już doszło do stanu ustalonego gdy e(t)=0. Polepszyło się. Idźmy dalej
Rozdz. 26.5.5 Regulacja PI Kp=3 Ti=5 sek
Rys. 26-24
Chyba trochę przesadziliśmy z intensywnością całkowania. Poprzednio było lepiej.
Rozdz. 29.5.6 Regulacja PI Kp=10 bez całkowania
Rys. 26-25
Stan ustalony zgodny z teorią dla regulacji typu P, czyli e(t)=0.
Rozdz. 26.5.7 Regulacja PI Kp=10 Ti=20 sek
Rys. 26-26
W 60 sek uchyb nie jest jeszcze zerowy. To zmniejszmy Ti. Zwróć uwagę na amplitudę oscylacji sygnału sterującego sPI(t) w porównaniu do amplitudy sygnału wyjściowego y(t). Na ogół jest większa.
Rozdz. 26.5.8 Regulacja PI Kp=10 Ti=10 sek
Rys. 26-27
Nie najgorzej. Ale nastawa Kp=3 Ti=8 sek z Rys. 26-23 jest lepsza dla sterowanego obiektu dwuinercyjnego. A przyzwyczailiśmy się do tego, że duże Kp jest przeważnie dobre. Zmniejszmy jeszcze Ti. Pomoże?
Rozdz. 26.5.9 Regulacja PI Kp=10 Ti=5 sek
Rys. 26-28
Nie pomogło. Za duże oscylacje.
Przejdźmy teraz do najtrudniejszego obiektu – trójinercyjnego.
Rozdz. 26.6 Regulator PI z obiektem trójinercyjnym
26.6.1 Obiekt trójinecyjny
Rys. 26-29
Obiekt trójinercyjny – K=1 i stałe czasowe T1=0.5 sek T2=3 sek, T3=5 sek.
W pierwszej chwili trudno odróżnić od dwuinercyjnego.
Im więcej inercji (tu T1,T2 i T3) tym wyraźniej zaznacza się parametr opóźnienia – tu To=1.3 sek.
Rozdz. 26.6.2 Regulacja PI Kp=3 bez całkowania
Rys. 26-30
Stan ustalony zgodny z teorią dla regulacji typu P.
Rozdz. 26.6.3 Regulacja PI Kp=3 Ti=16 sek
Rys. 26-31
Sygnał wyjściowy wolno dochodzi do stanu ustalonego y(t)=1.
Zwiększmy więc prędkość całkowania na Ti=10 sek.
Rozdz. 26.6.4 Regulacja PI Kp=3 Ti=10 sek
Rys. 26-32
Zwiększenie prędkości całkowania dało pożądany skutek. Po 45 sek. wystąpił stan x(t)=y(t), czyli e(t)=0. To zmniejszmy jeszcze Ti.
Rozdz. 26.6.5 Regulacja PI Kp=3 Ti=4 sek
Rys. 26-33
Jest gorzej. A co będzie gdy zwiększymy Kp?
Rozdz. 26.6.6 Regulacja PI Kp=10 bez całkowania
Czyli regulacja P.
Rys. 26-34
Zgodnie z teorią dla stanu ustalonego regulacji typu P po 60 sek wystąpi stan ustalony y(t)=0.91 i e(t)=0.09. W celu sprowadzenia uchybu regulacji e(t) do 0, włączymy na początek ostrożne (czyli wolne, czyli duże Ti) całkowanie.
Rozdz. 26.6.7 Regulacja PI Kp=10 Ti=16 sek
Rys. 26-35
Oscylacje y(t) występują wokół x(t)=1. W końcu w męczarniach po 60 sek. będzie osiągnięty zerowy uchyb regulacji. To zmniejszmy Ti, żeby było szybciej.
Rozdz. 29.6.8 Regulacja PI Kp=10 Ti=8 sek
Rys. 26-36
Jest gorzej. Czyli dla tego obiektu tróinercyjnego optymalnymi nastawami regulacji PI są Kp=3 i Ti=10 sek z Rys. 29-60. Przyzwyczailiśmy się, że Kp=10 dawało lepsze rezultaty niż Kp=3. Nie warto więc wpadać w przyzwyczajenia, zwłaszcza w automatyce. A co będzie, gdy jeszcze zwiększymy intensywność całkowania na Ti=2.5 sek?
Rozdz. 26.6.9 Regulacja PI Kp=10 Ti=2.5 sek
Rys. 26-37
Zauważ inny niż zwykle zakres oscyloskopu. Chociaż jest to układ niestabilny, to do 3 sek nic nie dzieje się na wyjściu bo też nic dzieje się na wejściu. W 3 sek “puknęliśmy” układ “Dirakiem” wyprowadzając go w ten sposób ze stanu równowagi.
Rozdz. 26.7 Regulacja PI z zakłóceniami
Rozdz. 26.7.1 Wstęp
Sterowane będą te same obiekty jedno- dwu- i trójinercyjne. Na ich wejścia będą działały sygnały wejściowe x(t) (tak jak do tej pory) oraz zakłócające z(t)=+0.5 lub z(t)=-0.5. Zakłócenia spowodują uchyb e(t), który tak będzie “denerwował” regulator PI, że zawsze sprowadzi go do 0. Ściślej. Składowa sterująca P sprowadzi uchyb do wartości bliskiej 0 a składowa całkująca I dokończy robotę sprowadzając go do 0. Eksperyment będzie trwał 2 minuty. Zastosowane będą te nastawy, które we wcześniejszych eksperymentach dawały “najładniejszą” odpowiedź. “Najładniejszą” tzn. względnie szybką i z możliwie małymi oscylacjami. Nazwijmy te nastawy optymalnymi chociaż mogą być jeszcze lepsze. Badalismy przecież tylko kilka kombinacji Kp, Ti.
Rozdz. 26.7.2 Inercyjny – zakłócenie dodatnie z(t)=+0.5, Kp=10, Ti = 5 sek
Zakłócenie z(t)=+0.5 pojawi się w 70 sekundzie.
Rys. 26-38
Do 70 sekundy, czyli do pojawienia się zakłócenia, przebieg jest taki sam jak na Rys. 26-18, biorąc pod uwagę inną skalę czasu na oscyloskopach. Początkowo zakłócenie z(t)=+0.5 spowodowało wzrost sygnału y(t) ale potem składowa I “zmusiła” y(t) do powrotu do poprzedniej wartości, czyli do y(t)=1. Odpowiada to sprowadzeniu uchybu e(t) do 0. Na dodatnie zakłócenie “grzanie”, sterowanie s(t) zareagowało zmniejszeniem mocy.
Rozdz. 26.7.3 Inercyjny zakłócenie – ujemne z(t)=-0.5, Kp=10, Ti = 5 sek
Zakłócenie z(t)=-0.5 pojawi się w 70 sekundzie.
Rys. 26-39
Na ujemne zakłócenie “chłodzenie”, sterowanie sPI(t) zareagowało zwiększeniem mocy.
Rozdz. 26.7.4 Dwuinercyjny – zakłócenie dodatnie z(t)=+0.5, Kp=3, Ti=8 sek
Zakłócenie z(t)=+0.5 pojawi się w 70 sekundzie.
Rys. 26-40
Obiekt “trudniejszy” do sterowania stąd dłuższe czasy regulacji.
Rozdz. 26.7.5 Dwuinercyjny zakłócenie ujemne z(t)=-0.5, Kp=3, Ti=8 sek
Zakłócenie z(t)=-0.5 pojawi się w 70 sekundzie.
Rys. 26-41
Na ujemne zakłócenie “chłodzenie”, sterowanie sPI(t) zareagowało zwiększeniem mocy.
Rozdz. 26.7.6 Trójinercyjny zakłócenie dodatnie z(t)=+0.5, Kp=3, Ti=10 sek
Zakłócenie z(t)=+0.5 pojawi się w 70 sekundzie.
Rys. 26-42
Jeszcze “trudniejszy” do sterowania i dłuższe czasy regulacji.
Rozdz. 26.7.7 Trójinercyjny zakłócenie ujemne z(t)=-0.5, Kp=3, Ti=10 sek
Zakłócenie z(t)=-0.5 pojawi się w 70 sekundzie.
Rys. 26-43
Na ujemne zakłócenie “chłodzenie”, sterowanie s(t) zareagowało zwiększeniem mocy. Uchyb e(t) został sprowadzony do 0.
