Podstawy automatyki
Rozdz. 31 Wpływ nieliniowości na Regulację
Rozdz. 31.1 Wstęp
Najbardziej wpływową nieliniowością na przebieg regulacji jest nasycenie we wzmacniaczu mocy (inna nazwa – człon wykonawczy) za regulatorem. Dlatego tytuł rozdziału mógłby być bardziej jednoznaczny – „Wpływ nasycenia członu wykonawczego na jakość regulacji”. Zaraz będziesz wiedział o co chodzi. Nawet jeden element nieliniowy „psuje” cały schemat . Nie możesz więc bezkrytycznie stosować poznanej dotąd teorii, w której wszystkie elementy były liniowe.
Przypomnienie o transmitancjach.
Gdy używasz transmitancji to znaczy, że siedzisz w obiektach liniowych. W obiektach tych sygnał wyjściowy y(t) w stanie ustalonym jest proporcjonalny do sygnału wejściowego y(t)![]()
Rys. 31-1
Charakterystyka obiektu liniowego w stanie ustalonym.
A w stanie nieustalonym (inaczej przejściowym) obiektami liniowymi rządzą równania różniczkowe liniowe, w których wszystkie współczynniki przy y(t), y'(t), y”(t),… x(t), x'(t),… są stałe. np. takie:![]()
Rys. 31-2
Równanie różniczkowe obiektu liniowego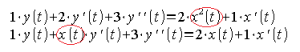
Rys. 31-3
Przykłady równań różniczkowych, które nie są liniowe
Czerwone obwódki to pluskwy przez które równanie różniczkowe nie jest liniowe, czytaj – trudne do rozwiązania.
Wróćmy do równania różniczkowego liniowego z Rys. 31-2, któremu odpowiada transmitancja G(s).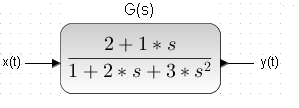
Rys. 31-4
Transmitancja G(s) którą opisuje równanie różniczkowe z Rys. 31-2
Dla ćwiczenia skojarz parametry 1, 2 i 3 licznika i 1, 2 mianownika powyższej transmitancji G(s) z równaniem różniczkowym liniowym z Rys. 31-2. Jak masz kłopoty to spójrz na Rys. 15-7 w rozdz. 15. Do tej pory cały czas zajmowaliśmy się obiektami liniowymi, nie licząc rozdziału o sterowaniu dwupołożeniowym. I tylko dla nich pojęcie transmitancji G(s) ma sens. Transmitancje G(s) odpowiadają równaniom różniczkowym liniowym, a te zostały już dawno rozgryzione przez matematyków. Dlatego teoria układów dynamicznych liniowych jest bardzo elegancka. Z transmitancji G(s) można względnie łatwo przewidzieć jak się będzie zachowywał układ po zamknięciu pętlą sprzężenia zwrotnego. Czy będzie stabilny? Jaki będzie stan ustalony? Jak dobrać parametry regulatora PID? Jeżeli na w schemacie blokowym pojawi się tylko 1 element nieliniowy, to (prawie na 100%) cały obiekt stanie się nieliniowy. Czyli taki, który nie da już się opisać równaniem różniczkowym liniowym.
Rozdz. 31.2 Elementy nieliniowe
Rozdz. 31.2.1 Wstęp
Przykłady elementów nieliniowych.
Rys. 31-5
Typową cechą każdego obiektu rzeczywistego (a nie idealnego!), jest to że prędzej czy później dochodzi do stanu nasycenia. Np. dla wzmacniacza nasyceniami są napięcia zasilania +/-15V. Widać to na powyższych charakterystykach. No, może oprócz Rys. 31-5d.
Typowe charakterystyki nieliniowe
Rys. 31-5a – „coraz szybciej rosnąca z nasyceniem” – Nazwa dziwna ale trafna.
Rys. 31-5b – liniowa z nasyceniem
Rys. 31-5c – „coraz wolniej rosnąca z nasyceniem”.
Rys. 31-5d – histereza. Zauważ, że wartość y(t) zależy od tego czy x(t) rośnie czy maleje. Tu akurat nie widać +/- nasycenia. Pojawiłyby się przy większych amplitudach sygnału wejściowego x(t).
Rys. 31-5e – liniowa ze strefą martwą i nasyceniem
W następnych 2 podpunktach na wejścia elementu:
-liniowego z nasyceniem (b)
-liniowego ze strefą martwą i nasyceniem (e)
podamy czarną sinusoidę x(t) i zbadamy czerwoną odpowiedź y(t).
Rozdz. 31.2.2 Badanie elementu liniowego z nasyceniem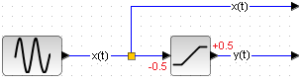
Fig. 31-6
Element liniowy z nasyceniem i wymuszeniem sinusoidalnym x(t)
Rys. 31-7
Nasycenie występuje przy y(t)=+/-0.5.
Przed osiągnięciem nasycenia x(t)=y(t)
Po nasyceniu
dla x(t)>0.5 y(t)=+0.5
dla x(t)<0.5 y(t)=-0.5
Gdyby nasycenie było +/-1 to cały czas byłoby x(t)=y(t) i widziałbyś czerwoną sinusoidę y(t).
Rozdz. 31.2.3 Element nieliniowy ze strefą martwą.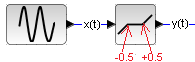
Rys. 31-8
Element nieliniowy ze strefą martwą i nasyceniem przy wymuszeniu sinusoidalnym x(t)
Fig. 31-9
Strefa martwa występuje dla -0.5….+0.5.
Gdyby strefa martwa była zerowa (inaczej- nie ma jej), to cały czas byłoby x(t)=y(t) i widziałbyś czerwoną sinusoidę y(t).
Gdyby strefa martwa była w zakresie -1…+1, to cały czas byłoby y(t)=0 i widziałbyś płaskie czerwone y(t)=0 i czarną sinusoidę x(t)
Rozdz. 31.3 Jak działa idealny układ automatyki?
Typowy układ regulacji z regulatorem PID i obiektem dwuinercyjnym. Poznałeś już go na Rys. 27-18 rozdz.27. Może to być np. regulator temperatury z wyjściem na grzałkę 1 kW. Grzałka zanurzona jest w niedużym zbiorniku z cieczą. Załóżmy, że ciecz jest idealna tzn. nie zamarza ani nie paruje. Spodziewamy się, że w stanie ustalonym będzie zerowy uchyb e(t), czyli y(t)=x(t)=+1.
Rys. 31-10
Niech +1 to +100°C.
I słusznie się spodziewamy e=0, bo jest składowa całkująca I. Temperatura wyjściowa już po 1.5 sek doszła do +100°C! Potem nastąpiło niewielkie przeregulowanie rzędu +5 °C i po 10 sek wystąpił stan ustalony y(t)=x(t)=+100°C. Za to sygnał sterujący sPID(t) ma duże przeregulowania. Moc „dodatnia”- grzanie jest chwilami większa od +2, moc „ujemna”-chłodzenie mniejsza od -1. Dlatego temperatura y(t) bardzo szybko, już po 1.5 sek doszła do stanu ustalonego, chociaż obiekt ma 2 inercje 3 sek i 5 sek! To jest właśnie dobra robota ujemnego sprzężenia zwrotnego, ogólniej – automatyki. Gdyby to był układ otwarty, czytaj bez sprzężenia zwrotnego, czytaj bez automatyki, to trwałoby to pół minuty a nie tylko 1.5 sek. Ty też gotując zupę stosujesz ujemne sprzężenie zwrotne. Podkręcasz gaz na full a potem zmniejszasz, gdy temperatura osiągnie punkt wrzenia. Trochę się rozgadałem, wróćmy więc do przebiegu.. Wyraźnie widać sygnał sterujący sPID(t) obcięty przez oscyloskop na poziomie -1 i +2 czyli -100°C…+200°C. Aby zobaczyć jak wielkie są te przeregulowania sygnału sterującego sPID(t), zmieńmy zakres oscyloskopu z -1…+2 na -20…+160. Czyli na -2000°C…+16000°C! Przypominam, że w naszym kursie istnieje temperatura -2000°C, a nawet niższa.
Rys. 31-11
Co prawda sygnały x(t), y(t) wielkości ok. +100°C są teraz ledwo widoczne, za to widzisz całe sPID(t). Na początku sygnał sterujący sPID(t) waha się w granicach -5…+160. Czyli przez krótki moment moc dodatnia (grzejna) „chce” podgrzać ciecz do +16000°C a za chwilę moc ujemna „chce” schłodzić do -500°C! W stanie ustalonym grzałka sterująca ciągnie 1kW, za to w czasie piku aż 160 kW! Żaden konstruktor nie da przecież takiej wielgachnej grzały! Najwyżej 1.5 kW. Także rzadko stosuje się moc ujemną-chłodzenie.
Dlatego ograniczeniem będzie węższy zakres 0…1.5 zamiast -5…+160 . Nawet jeszcze węższy. Przecież przy wyłączonej mocy temperatura spada nie do 0°C lecz do temperatury otoczenia np. +20°C. Tym właśnie różni się teoria od praktyki*. Systemy liniowe które do tej pory rozpatrywaliśmy, są eleganckie, łatwe (względnie, względnie!) i dają odpowiedź na wiele ogólnych pytań. Stabilność, Hurwitz itd. Natomiast systemy rzeczywiste – nieliniowe będą odbiegać od liniowych.
Jak daleko odbiegać? Na ile ich liniowe przybliżenie jest wiarygodne? O tym będzie mowa za chwilę.
* Kiedyś w zacnej firmie automatycznej widziałem plakat z jej dewizą:
– Praktyk – Wszystko działa, ale nie wie dlaczego.
– Teoretyk– Nic nie działa, ale wie dlaczego.
My łączymy teorię z praktyką. Nic nie działa i nie wiemy dlaczego.
Od razu ich polubiłem.
Rozdz. 31.4 Jak działa rzeczywisty układ automatyki?
Rozdz. 31.4.1 Wstęp
W życiu nie ma ideałów. Transmitancja G(s) jest tylko przybliżeniem systemu rzeczywistego. Nasuwa się pytanie. Jak daleko odbiega ono od rzeczywistości. Pierwszym przybliżeniem systemu rzeczywistego jest coś takiego.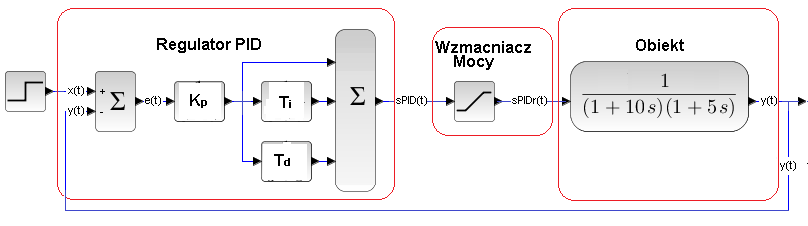
Rys. 31-12
W następnych punktach spróbuję uzasadnić, że nieliniowość wprowadzana jest główne przez Wzmacniacz Mocy. Dlatego kolejno rozpatrzymy pod tym względem Wzmacniacz Mocy, Regulator PID i Obiekt
Rozdz. 31.4.2 Wzmacniacz Mocy z Nasyceniem
Schemat różni się od Rys. 31-10 tylko Wzmacniaczem Mocy w środku schematu. Do tej pory zakładaliśmy, że sygnał z regulatora sPID(t) zawsze ma wystarczającą moc do wysterowania obiektu. Wiadomo, że tak nie jest. Każdy wzmacniacz ma swoje nasycenia. Nawet elektrownia w Bełchatowie nie da więcej niż 4 000 MW. To też jest gigantyczny wzmacniacz mocy. Wejściem jest pokrętło (nie ważne, że komputerowe) mocy w Centralnej Dyspozytorni, a wyjściem moc oddana do sieci.
Wzmacniacz Mocy na schemacie to nic innego jak element liniowy z nasyceniem z Rys. 31-5b. Nie musi występować w wersji elektrycznej. Może to być np. zawór z siłownikiem. Sygnał z regulatora steruje stopniem otwarcia zaworu, pośrednio więc przepływem np. dopływem pary do turbiny. Przepływ F nie będzie dowolny, tylko w granicach 0…Fmax Czyli znowu mamy jakiś tam Wzmacniacz Mocy. Elektryczny wzmacniacz mocy lub zawór lub coś tam jeszcze, noszą wspólną nazwę- Człon Wykonawczy. Mamy Człon Wykonawczy, który jako element nieliniowy psuje cały schemat. Psuje, czyli nie można obliczyć transmitancji całego układu zamkniętego. A co z PID-em i obiektem?
Rozdz. 31.4.3 Regulator PID
To już prawie idealny układ liniowy o transmitancji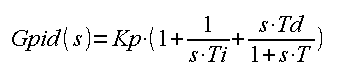
Rys. 31-13
Nastawy regulatora mogą być np. następujące:
Kp=10
Ti =7 sek
Td=2 sek (różniczkowanie, jak w każdym porządnym regulatorze jest rzeczywiste, tzn. z inercją T)
Jeszcze komentarz do „prawie idealny układ liniowy”. Współczesne regulatory PID realizowane są przeważnie w technice mikroprocesorowej. Czyli odpowiedź regulatora nie jest ciągła lecz kwantowana przez zegar. Jednak przy częstym kwantowaniu odpowiedź regulatora możemy traktować jako ciągłą. Na wyjściu regulatora jest przetwornik cyfrowo/analogowy. Czyli na wzmacniacz mocy wchodzi sygnał ciągły. Z założenia wzmacniacz mocy wcześniej wejdzie w nasycenie niż PID. Dlatego z czystym sumieniem możemy traktować PID jako transmitancję Gpid(s)
Rozdz. 31.4.4 Obiekt G(s)
Obiektem może być piec, kolumna rektyfikacyjna albo rakieta. Każdy z nich ma oczywiście inne własności dynamiczne. Na Rys. 31-12 przykładowym obiektem jest człon dwuinercyjny. Czyli milcząco założyliśmy, że jest to człon liniowy o transmitancji G(s).
Dla obiektu są słabsze argumenty dotyczące liniowości niż dla PID-u. Charakterystyka statyczna większości typowych obiektów jest „coraz wolniej rosnąca z nasyceniem” –>Rys. 31-5c.
Co z tego wynika? To że mianownik, czyli nachylenie charakterystyki równe jest jedności dla zerowego punktu pracy. a potem się zmniejsza. Tak samo stałe czasowe mogą się zmieniać w pewnych granicach. Tak że parametry „prawdziwej” transmitancji mogą zależeć od punktu pracy i prawdziwa wartość jest jakby rozmyta w granicach.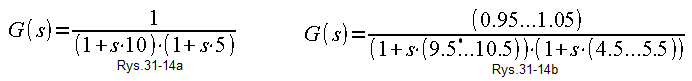
Rys. 31-14
Rys. 31-15a-na podstawie obserwacji obiektu, lub na podstawie modelu matematycznego obiektu zakładamy, że jest to obiekt dwuinercyjny o wzmocnieniu k=1, stałych czasowych T1=10 sek i T2=5 sek.
Rys. 31-15b-Prawdziwe parametry mogą być,w zależności od punku pracy i błędu pomiaru, w zakresach k=0.95…1.05, T1=9.5…10.5 sek i T2 4.5…5.5 sek.
Wiele obiektów, zwłaszcza wieloinercyjnych, da się przybliżyć jako inercję z opóźnieniem. Po co? Przecież lepszy jest model dokładny niż przybliżony. Tak jak lepiej być zdrowym i bogatym niż biednym i chorym.
Po pierwsze, łatwiej wyznaczyć parametry K, T i To obserwując odpowiedź na skok jednostkowy.
Po drugie dla tak wyznaczonej transmitancji, są już gotowe parametry nastaw regulatora PID. Wtedy odpowiedź układu sterowanego przez PID jest optymalna przy jakimś kryterium. Np. najkrótszy czas regulacji przy możliwie małych przeregulowaniach.
O inercji z opóźnieniem To i wzmocnieniu K była już mowa dużo wcześniej. Dla przypomnienia pokażę odpowiedź y(t) na skok jednostkowy x(t).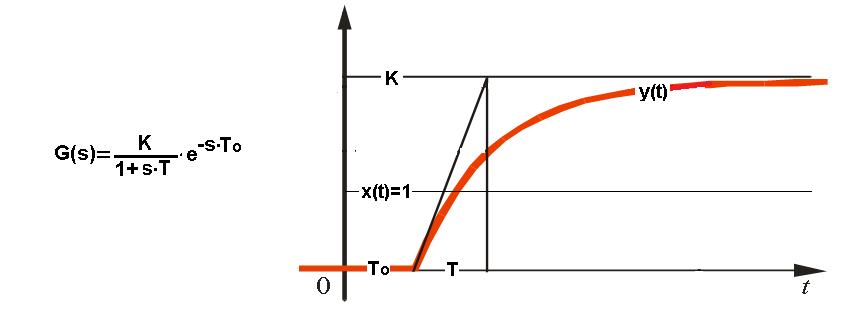
Rys. 31-15
Inercja z opóźnieniem
Rozdz. 31.4.5 Wnioski
W nawiązaniu do Rys. 31-12 stwierdziliśmy że:
– Regulator PID jest obiektem liniowym o transmitancji Gpid(s)–>Rys. 31-13
– Z pewną dozą wyrozumiałości, obiekt G(s) też jest obiektem liniowym. Tym bliżej liniowości im mniejszy sygnał wejściowy. Często obiekty przybliżane są inercją z opóźnieniem.
– Człon Wykonawczy jest elementem liniowym z nasyceniem, czyli jest elementem nieliniowym. Głównie on „psuje” cały układ pozbawiając go liniowości. Czyli nie da się policzyć transmitancji układu zamkniętego Gz(s) z Rys. 31-12.
– Cała do tej pory wyłożona teoria–>badanie stabilności, dobór nastaw regulatora itd…, dotyczy układów liniowych.
Biorąc pod uwagę to, że w rzeczywistych układach regulacji zawsze występuje Człon Wykonawczy możemy dojść do wniosku, że cała teoria sterowania to tylko piękna błyskotka matematyczna. Nie ma w niej korzyści materialnych, tylko duchowe. Na szczęście nie jest tak do końca.
Rozdz. 31.5 Porównanie układu idealnego i rzeczywistego
Rozdz. 31.5.1 Wstęp
Będziemy badać odpowiedź na skoki jednostkowe x(t)=+1, oraz zakłócenia z(t)= +0.4 i z(t)=-0.4 przy nasyceniach członu wykonawczego 0…+1.5 i 0…+5 Na zdrowy rozum spodziewamy się, że im później wystąpi nasycenie, tym bardziej idealny jest system. Także zmniejszenie amplitudy skoku x(t) powoduje ten sam efekt. A co z zakłóceniem z(t)? Okaże się, że reakcje na małe zakłócenie zakłócenie są podobne dla układów rzeczywistych i idealnych. Tym bardziej im mniejsze zakłócenia.
W następnych doświadczeniach regulator PID o nastawach Kp=10, Ti=7 sek, Td=1.5 sek będzie sterował obiektem dwuinercyjnym o parametrach K=1, T1=10 sek i T2=5 sek.z Powyższe nastawy regulatora dobraliśmy wcześniej metodą prób i błędów jako optymalne dla tego obiektu. Zakładając oczywiście, że obiekt był idealnie liniowy.
Rozdz. 31.5.2 Nasycenie 0…+1.5, x(t)=+1, z(t)=+0.4 (grzanie)
Mamy 2 takie same zbiorniki z identyczną cieczą obok siebie. Parametry regulatorów też są identyczne. Różnica jest tylko w mocy grzałek.
Pierwszy system-idealny ma moc nieograniczoną. Czyli nie występują żadne nasycenia. Może on dać nawet moc grzania +1000 000kW i moc chłodzenia -1000 000kW.
Drugi system-rzeczywisty ma już prawdziwy człon wykonawczy tzn. grzałkę z mocą ograniczoną +1.5 kW. Dodatkowo sygnał ujemny z regulatora nie chłodzi tylko wyłącza grzałkę. Temperatura spada wtedy do otoczenia np. do 0°C. Czyli zakres regulatora to 0…+1.5 kW. Zakłóceniem jest włączenie grzałki o mocy +0.4 kW. Wartość zadana x(t) i zakłócenie z(t)+0.4 działają równolegle na 2 systemy.
Na pewno Idealny będzie lepszy od Rzeczywistego. Ale o ile lepszy? Czy to będzie 100:0 czy tylko 5:2?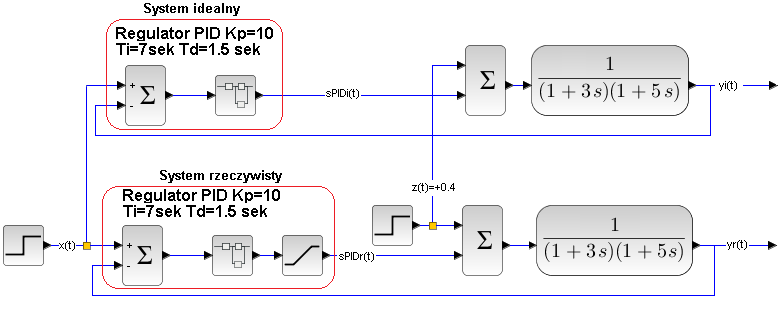
Rys. 31-16
Na górze jest system idealny, czyli z członem wykonawczym bez nasyceń.
Na dole jest system rzeczywisty z członem wykonawczym o nasyceniach 0…+1.5.
Jak to interpretować? Maksymalna wartość regulatora odpowiada mocy grzałki +1.5 kW, która w stanie ustalonym da temperaturę cieczy +150°C. Dolne nasycenie 0 kW to wyłączona grzałka i temperatura spada wtedy do temperatury otoczenia, np. do 0ºC.
Rys. 31-17
Do 60 sek mamy tylko samo x(t)=1, w 60 sek wystąpi zakłócenie +0.4-grzanie.
SYSTEM IDEALNY-człon wykonawczy bez nasycenia
Sygnał sterujący sPIDi(t) szybko doprowadził do stanu yi(t)=1 w którym uchyb ustalony jest zerowy. Charakterystyczne są bardzo duże wahania sygnału sterującego sPID(t) na początku skoku x(t)–>Rys. 31-11. W 60 sekundzie mamy zakłócenie z(t)=+0.4–> włączenie dodatkowej grzałki o mocy 0.4 kW. Regulator PID prawidłowo ocenił sytuację i zmniejszył moc też o 0.4 kW. Był oczywiście krótki stan przejściowy, ale wszystko skończyło się tak jak trzeba.
SYSTEM RZECZYWISTY człon wykonawczy z nasyceniem
Poprzednio sygnał sterujący sPIDi(t) mógł hulać w granicach -nieskończoność …+nieskończoność , obecnie człon wykonawczy daje tylko skromne sPIDr(t) w granicach 0…+1.5. Dlatego zamiast szpili 160 jest zielony płaszczak o amplitudzie +1.5 od początku skoku do około 18 sek. Dobre i to. W tym czasie yr(t) dąży do +1.5 zamiast do 160. Dlatego yr(t) wolniej narasta. W dodatku jest duże przeregulowanie do ok. +1.3, bo hamowanie od członu różniczkującego D jest słabsze niż w idealnym. Zauważ, że potem zielony sygnał sterujący sPIDr(t) już nie wchodzi w nasycenia i dlatego yr(t) dochodzi do 1 w stanie ustalonym (uchyb zerowy), jak w każdym porządnym systemie liniowym czyli idealnym. Mimo tego, że przeregulowanie i czas regulacji są większe w systemie rzeczywistym to nie są 100 razy większe, jakby wynikało z maksymalnych sygnałów sPIDi(t)=+160 i sPIDr(t)=+1.5.
W 60 sekundzie wystąpiło zakłócenie z(t)=+0.4. Przebiegi yr(t) i yi(t) idealnie się pokrywają, ponieważ nie zadziałało żadne nasycenie. System rzeczywisty “myśli”, że jest idealnym.
Wniosek
Nieliniowość, w tym głównie nasycenie wzmacniacza mocy (członu wykonawczego), pogarsza oczywiście jakość regulacji, ale nie tak bardzo!
Uwaga której możesz nie czytać, bo już było coś na ten temat
Co robią Kp, Ti, Td?
Kp=10-składowa proporcjonalna
Szybko sprowadza sygnał wyjściowy yi(t) do wartości 0.91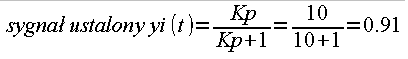
Rys. 31-18
Czyli składowa Kp nie zapewnia zerowego uchybu regulacji.
Ti=7sek-składowa całkująca
Sprowadza uchyb do zera. Pytanie. Skoro składowa całkująca sprowadza uchyb do zera, to po kiego licha jest Kp? Odpowiedź jest prosta. Kp szybko sprowadza yi(t) do wartości 0.91. Składowa I też od samego początku sprowadza uchyb do zera, ale robi to powoli. W skrócie i niezbyt precyzyjnie – Kp szybko robi yi(t)=0.91, a za resztę, czyli za doprowadzenie yi(t) do 1, odpowiada właśnie Ti.
Td=1.5 sek-składowa różniczkująca
Jeszcze bardziej niż Kp przyspiesza dojście do yi(t)=1. Na początku skoku Kp daje kopa w sygnale sPID(t) do wartości 10, zaś za resztę czyli za 150, odpowiada składowa różniczkująca, czyli Td. Przecież toto różniczkuje skok x(t). I tak całe szczęście, że jest to różniczkowanie rzeczywiste a nie idealne. Wtedy mielibyśmy nieskończenie wielką szpilę, a nie nędzne sPID(t)=160.
Wróćmy do tego kopa od skoku x(t). Dzięki niemu yi(t) bardzo szybko rośnie. Tak jakby chciał dojść nie do 1 ale do 160. Za chwilę x(t) jest płaskie–> sPID szybko spada. Ale za to działa różniczkowanie od narastającego yi(t). I to działa w kierunku przeciwnym niż początkowego kopa 160! Przez chwilę daje nawet wartości ujemne sPID(t). A co to oznacza? Że składowa Td działa teraz hamująco czyli stabilizująco. Zapobiega przeregulowaniom, a nawet niestabilnościom
Rozdz. 31.5.3 Nasycenie 0…+1.5, x(t)=+1, z(t)=-0.4 (chłodzenie)
Schemat różni się od Rys.31-16 tylko zakłóceniem.
Poprzednio było z(t)=+0.4-grzanie, teraz jest z(t)=-0.4-chłodzenie
Rys. 31-19
Przebiegi do 60 sek są identyczne z Rys. 34-18. Na zakłócenie z(t)=-0.4-chłodzenie, regulator zareagował prawidłowo zwiększając moc grzania o +0.4. Sygnał sterujący nie wszedł w nasycenie, regulator „myśli”, że system jest liniowy. Dlatego sygnały sPIDi(t) i sPIDr(t) pokrywają się.
Rozdz. 31.5.4 Nasycenie 0…+5, x(t)=+1, z(t)=+0.4 (grzanie)
Ten i następny schemat różnią się od poprzednich tylko nasyceniami. Teraz będzie większe 0…+5 zamiast 0….+1.5. Większe tzn. system jest bardziej „idealny”, czyli spodziewamy się lepszej regulacji. Mamy teraz człon wykonawczy o większej mocy–>czytaj droższy.
Rys. 31-20
Na Rys. 31-17 widziałeś wpływ nasycenia +1.5 na sygnał sterujący rzeczywisty sPIDr(t)– (za wzmacniaczem mocy). Tu jest większe górne nasycenie – +5 i dlatego nie widzisz tego zielonego płaskiego sPIDr(t). Większe maksymalne sPIDr(t) spowodowało szybszą regulację i mniejsze przeregulowanie. Można powiedzieć że system zbliżył się do idealnego. Reakcja na zakłócenie nie poprawiła się, bo i tak jest taka taka sama, jak dla systemu idealnego. Dlaczego? Bo sygnał sterujący sPIDr(t) nie wszedł w nasycenie.
Rozdz. 31.5.5 Nasycenie 0…+5, x(t)=+1, z(t)=-0.4 (chłodzenie)
Schemat różni się od poprzedniego tylko zakłóceniem z(t)=-0.4 (chłodzeniem).
Rys. 31-21
Różnica jest tylko w reakcji na zakłócenie z(t)=-0.4-chłodzenie.
Rozdz. 31.5.6 Wnioski
W porównaniu do systemu Idealnego system Rzeczywisty wolniej i z większymi przeregulowaniami dochodzi do stanu ustalonego. Jest to oczywiście pewną wadą, ale da się z tym żyć. Zwłaszcza, że jest zapewniony zerowy uchyb ustalony i tłumienie zakłóceń jest prawie identyczne jak w idealnym. Weź też pod uwagę to, że system automatyki głównie tłumi zakłócenia z(t), zaś zmiany wartości zadanej x(t) są znacznie rzadsze. Chociaż system idealny daje na początku skoku ponad 100 razy większego kopa , niż rzeczywisty (160 do 1.5), to reakcja nie jest 100 razy gorsza-czytaj wolniejsza. Dlatego możemy traktować systemy rzeczywiste prawie tak jak liniowe. Ale tylko wtedy, gdy x(t) jest między nasyceniami członu wykonawczego–> w naszym przypadku x(t)=0…+1.5. Ten warunek nie jest trudny do spełnienia. A to znaczy, że dla systemów rzeczywistych możemy korzystać z całej bogatej wiedzy dla systemów liniowych.
Wracając zaś do piłki nożnej, to relacje między systemem Idealnym a Rzeczywistym,
to bardziej Niemcy-Polska niż Niemcy-Gibraltar.
Rozdz. 31.6 Jak działa regulacja, gdy wartość zadana x(t) jest większa od nasycenia?
Rozdz. 31.6.1 Pierwsze podejście-tylko x(t), yi(t) i yr(t)
Maksymalna moc za regulatorem to +0.95 kW, która jest w stanie podgrzać ciecz do temp. +95°C. A gdyby regulacja wymagała podgrzania do +105 °C? To tak, jakby kierownik żądał od pracownika wykonania zadania powyżej jego kompetencji.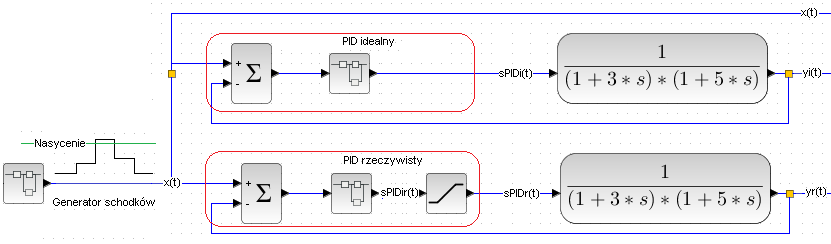
Rys. 31-22
Tym razem nie będzie to pojedynczy skok jednostkowy wartości zadanej x(t), lecz sygnał z generatora schodków. Regulator PID rzeczywisty ma na wyjściu wzmacniacza mocy ograniczenia 0…+0.95.
Wystąpią 3 okresy dla schodkowego x(t) w których:
Okres 1
x(t)=+0.3 (poniżej nasycenia)
Okres 2
x(t)=1.05 (powyżej nasycenia!)
Okres 3
x(t)=+0.5 (znowu poniżej nasycenia)
Reakcje idealnego yi(t), czyli bez nasycenia, są oczywiste. Zadziała ujemne sprężenie zwrotne, które sprowadzi uchyb zera. Sygnał yi(t) stara się naśladować x(t). Cały dotychczasowy kurs próbował Cię do tego przekonać. A reakcje regulatora z nasyceniem czyli rzeczywistego? Spróbuj je przewidzieć. Na razie nie interesują nas sygnały “wewnętrzne” sPID(t), sPIDir(t) i sPIDr(t) z Rys. 31-22.
Rys. 31-23
Działanie idealnego regulatora yi(t), zawsze jest lepsze od rzeczywistego yr(t). Dlatego zbadajmy tylko rzeczywiste yr(t).
Okres 1. x(t)=+0.3
Wartość zadana x(t) jest mniejsza od nasycenia=+0.95. Zadziała więc sprzężenie zwrotne. Sygnał yr(t) dojdzie do wartości x(t)=yr(t)=+0.3.
Okres 2. x(t)=+1.05
Wartość zadana x(t) każe osiągnąć regulatorowi rzeczywistemu stan yr(t)=+1.05, czyli temperaturę na wyjściu+105°C. Ale jak biedaczysko PID ma to zrobić, skoro człon wykonawczy ma nasycenie +0.95? Nie da się! Po prostu yr(t) będzie dążyło do +0.95. Nie zadziała ujemne sprzężenie zwrotne! Tak, jakby to był układ otwarty.
Widać to zresztą na przebiegu, gdzie dopiero pod koniec okresu 2 sygnał yr(t) osiągnął stan ustalony +0.95.
Okres 3. x(t)=+0.5
Wartość zadana x(t) jest mniejsza od nasycenia=+0.95. Zadziała więc ujemne sprzężenie zwrotne które sprowadzi uchyb do zera–>yr(t)=x(t)=+0.5. Oczywiście rzeczywiste yr(t) jest wolniejsze (gorsze!) od idealnego yi(t). Ale skąd wziął się dodatkowy czas martwy, którego nie było w okresie 1? Przecież wtedy nie było tego zjawiska. Czas martwy to dodatkowe opóźnienie To, które zawsze jest niekorzystne dla regulacji!
Rozdz. 31.6.2 Drugie podejście-dokładniejsze
Do poprzedniego schematu dodamy obserwację sygnał sterującego idealnego żółtego sPIDi(t) i rzeczywistego czarnego sPIDr(t) z Rys.31-22. Może dowiemy się czegoś o czasie martwym?
Rys. 31-24
Sygnały systemu idealnego są oczywiste. Silniejsze i krótsze sPIDi(t) spowodowało jak zwykle szybką odpowiedź yi(t) które wyraźnie stara się naśladować w schodkowe x(t) w okresach 1, 2 i 3.
Rozpatrzmy w takim razie system z regulatorem rzeczywistym, czyli z nasyceniem.
W okresie 1 regulator nie wszedł w nasycenie. Dlatego zadziałało ujemne sprzężenie zwrotne i sygnał yr(t) starał się śledzić schodkowe x(t). Robił to jednak gorzej (dłużęj!) niż idealny, chociaż w stanach ustalonych też dawał zerowy uchyb–>x(t)=yr(t)–>e(t)=0! Zauważ też, że w stanie ustalonym rzeczywisty sygnał sterujący sPIDr(t)=yr(t). Podobnie jak w idealnym sPIDi(t)=yi(t)
W okresie 3 jest podobnie, tylko nie wiadomo skąd pojawił się czas martwy. Najważniejsze, że zadziałało sprzężenie zwrotne i yr(t) doszło do x(t)=+0.5.
W okresie 2 regulacja weszła w nasycenie. Tzn. x(t)=1.05 jest większe od nasycenia=0.95 maksymalnego sygnału regulatora rzeczywistego tj. sPIDr=0.95. A to oznacza, ze nie działa ujemne sprzężenie zwrotne i yr(t) dochodzi do stanu ustalonego yr=0.95 jak w układzie otwartym.
Rozdz. 31.6.3 Trzecie podejście-jeszcze dokładniejsze
Obserwujemy żółte idealne sPIDi(t), czarne rzeczywiste sPIDr(t) oraz zielone sPIDir(t) przed wzmacniaczem mocy z Rys.31-22
Rys. 31-25
System Idealny
Przebieg żółtego sPIDi(t) jest oczywisty i nie wymaga komentarza.
System Rzeczywisty
Zielony sygnał sPIDir(t) z przed członem wykonawczym może mieć dowolną wartość numeryczną, ponieważ jest obliczany przez mikroprocesor i nie zawiera mocy. Literka i w sPIDir(t) sugeruje, że sygnał jest za częścią idealną rzeczywistego regulatora PID.
Okres 1 x(t)=+0.3
Do czasu tz=6.5 sek zielony sygnał sPIDir(t) jest większy od nasycenia +0.95. Objawi się to obcięciem sygnału za wzmacniaczem mocy czarnego sPIDr(t). Wtedy yr(t) dąży do +0.95 jak w układzie otwartym. Sprzężenie zwrotne pojawi po tz=6.5 sek, gdy sPIDi(t) spadnie poniżej +0.95. Wtedy szybko sprowadzi sygnał wyjściowy yr(t) do wartości yr(t)=x(t)=0.3. Szybko ale oczywiście wolniej niż yi(t) w systemie Idealnym.
Okres 2 x(t)=+0.95
Zielone sPIDir(t) skoczył do góry. A co się z nim dzieje dalej, to nie widać bo za mały zakres oscyloskopu. Tak czy owak sygnał za wzmacniaczem mocy jest obcięty na poziomie sPIDr(t)=+0.95 i yr(t) dążydo+0.95 tak jak w układzie otwartym (bez sprzężenia zwrotnego). Nie widzisz całego zielonego sPIDir(t)! A tam dzieją się rzeczy ciekawe. Przekonasz się o tym w następnym doświadczeniu.
Okres-3 x(t)=+0.5
Chyba coś świta z czasem martwym. Widać, że w tym czasie yir(t) jest większe od +0.95. Wtedy yr(t) jest w przybliżeniu obcięte na poziomie też +0.95. Gdy yir(t) stanie się mniejsze od +0.95 to sprzężenie zwrotne doprowadzi yr(t) do +0.5.
Rozdz. 31.6.4 To samo tylko większy zakres oscyloskopu
Otrzymamy wizualnie ten sam schemat, ale z innym zakresem oscyloskopu -100…+140, poprzednio -1+2. Dzięki temu zobaczysz to, co było niewidoczne na Rys. 31-25.
Rys. 31-26
Sygnały x(t), yi(t), yr(t) są teraz tyci, tyci. Za to widoczne są sygnały sterujące sPIDi(t) i sPIDir(t). Zielone sPIDir(t) przeważnie zasłania żółte sPIDi(t).
Okres 1 x(t)=+0.3
Opadająca zielona szpila yir(t) do czasu tz=6.5 sek. Nie widziałeś tego na Rys. 31-25.
Okres 2 x(t)=+0.95
Cały czas nie działa sprzężenie zwrotne bo sPIDir(t)>0.95. Dlatego mamy klasyczną odpowiedź PID-u na dodatni skok jednostkowy w układzie otwartym!
Okres 3 x(t)=+0.5
Wartość zadana x(t) spadła z +1.05 na +0.5. Czyli mamy znów klasyczną odpowiedź PID-u na ujemny skok jednostkowy x(t). Wyraźnie widać teraz, że czas martwy to dochodzenie składowej całkującej regulatora PID do takiej wartości w której sPIDir(t) stanie się mniejsze od nasycenia +0.95. Potem sprzężenie zwrotne sprowadzi yr(t) do wartości yr(t)=x(t)=0.5–> zerowy uchyb regulacji.
Rozdz. 34.6.5 Wnioski
1. Jeżeli regulator rzeczywisty „każe” obiektowi wejść w stan który jest możliwy do spełnienia* przez wzmacniacz mocy, to regulacja działa w sposób podobny do systemu idealnego. Odpowiedź yr(t) jest oczywiście wolniejsza (gorsza) niż dla idealnego, ale w końcu yr(t)=x(t) czyli zapewniony będzie zerowy uchyb regulacji.
2. Jeżeli regulator rzeczywisty „każe” obiektowi wejść w stan który nie jest możliwy do spełnienia, czyli gdy x(t)>0.95 to sygnał wyjściowy yr(t) wolno dojdzie do stanu nasycenia tak jak w układzie otwartym–> okres 2 na Rys. 31-25.
3. Jeżeli regulator wychodzi ze stanu nasycenia, tak jak w okresie 3 na Rys. 31-25 to wystąpi wtedy czas martwy. Przyczyną tego jest składowa całkująca regulatora–>okres 3 na Rys.31-26. Inna nazwa czasu martwego regulatora PID to strefa martwa całkowania.
Jak walczyć ze strefą martwą całkowania?
Czas martwy To wprowadza do systemu opóźnienie które jest oczywiście zjawiskiem niekorzystnym. Bo czy chciałbyś prowadzić samochód, w którym kierownicą skręcisz w lewo, a koła zareagują dopiero po To=1 sek?
Obecnie regulatory wykonane są w technice mikroprocesorowej. Dlatego gdy regulator stwierdzi, że pomimo wzrastającego od składowej całkującej sygnału sterującego, sygnał wyjściowy nie wzrasta , to wyłącza on składową całkującą. Czyli w stanie nasycenia z regulatora PID robi się regulator PD.
Jest to przykład regulatora o zmiennej strukturze. To przełączenie może wystąpić np. od wejścia wzmacniacza mocy w stan nasycenia, a to jest łatwe wykrycia przez regulator mikroprocesorowy.
