Scilab

Rozdział 4.2 Pierwszy program P4-1
Jest to raczej okazja do zapoznania się z edytorem Scinotes i jego współpracą z Konsolą. Sam program to prościzna.
Tak go wykonasz.
– Skopiowanie P4-1 z kursu 
– Wywołanie Scilaba
– Wywołanie edytora Scinotes w programie Scilab
– Skopiowanie P4-1 do edytora Scinotes
– Zapisanie i wykonanie P4-1 w dowolnym miejscu*
– Wykonanie P4-1 na konsoli w wersji “z echem” i “bez echa”.
*Jeżeli Ci zależy, to możesz go zapisać w konkretnym folderze, który stworzysz wcześniej. Ale nie jest to konieczne. Następne programy będą nadpisane właśnie w tym “gdzieś go zapiszesz”. Gdzie? Nie ma to znaczenia. Przecież i tak w każdej chwili możesz go skopiować z kursu do edytora Scinotes.
Powyższe etapy pokazano na animacji Rys. 4-1. 
Program P4-1 

clear; clc;// czyszczenie zmiennych i ekranu
x=4
y=2
z=x+y
disp(z) 

Rys. 4-1
Jak wykonać w Scilabie program P4-1?
Radzę bardzo dokładnie zidentyfikować wszystkie etapy. Tak będziesz postępował przy następnych programach. Ich obsługa jest podobna, dlatego większość z nich będzie bez animacji.
Najpierw został wykonany tzw. program bez echa, potem ten sam program z z echem 
Program z echem pokazał na konsoli wyniki wszystkich  instrukcji
Program bez echa pokazał na konsoli tylko wynik instrukcji wyświetlającej disp(z) 
Wniosek
Programista zwykle rozpoczyna testowanie programu z echem. Widzi co się dzieje w każdej instrukcji.
Potem, gdy znalazł błędy  (tzw. debugowanie), to testuje program bez echa. 

Rozdział 4.3 Instrukcje wejścia i wyjścia
Po wpisaniu do edytora Scinotes i wykonaniu programu P4-2 będziesz wiedział jak działają instrukcje wejścia typu x=input(‘Wprowadź daną’) oraz instrukcje wyjścia typu y=disp(‘daną jest’, x)

Program P4-2

clear;clc;
x=input('wprowadź pierwszą liczbę ')
y=input('wprowadź drugą liczbę ')
z=x+y
disp('Sumą dwóch liczb jest',z)

Po spotkaniu pierwszej instrukcji tj. x=input(‘wprowadź pierwszą liczbę ‘)*, program się zatrzyma i czeka na wprowadzenie przez Ciebie jakiejś liczby. Wtedy zapisze ją jako x. Pamiętaj, żebyś wcześniej kliknął w dowolne miejsce okna Konsola! Tak samo postąp z instrukcją y=input(‘wprowadź drugą liczbę ‘). Instrukcja z=x+y jest oczywista. 
Uwaga:
Będziemy wywoływać tylko program bez echa. Nie wiem dlaczego, ale program z echem  zawierający instrukcje wejścia, nie działa prawidłowo.
Wykonanie programu przedstawiono  na poniższej animacji.

Rys. 4-2
Program z instrukcjami wejścia i wyjścia
Rysunek przedstawia stan końcowy animacji.
1. Wywołaj edytor Scinotes
2. Skopiuj z Kursu program P4-2
3. Wklej P4-2 do Scinotes
4. Kliknij zapisz jako… (tu nadpiszemy jako ….dokumenty/1.sci) (jak nie zapiszesz, to program się nie wykona!)
5. Wykonaj jako plik bez echa (pamiętaj, że jesteś jeszcze w edytorze Scinotes. Dlatego kliknij okno Scilaba, aby wprowadzać dane)
6. Pojawił się komunikat “wprowadź pierwszą liczbę” 
7. Wpisałem 4 i kliknąłęm Enter
8. Pojawił się komunikat “wprowadź drugą liczbę” 
9. Wpisałem 3 i kliknąłęm Enter
10. Pojawił się komunikat
“Sumą dwóch liczb jest
    7″
Dokładnie przeanalizuj działanie programu. Także stany Przeglądarki zmiennych.
Trochę nieładny jest końcowy komunikat gdzie 7 jest w następnym rzędzie. Lepiej byłoby “Sumą dwóch liczb jest 7”
Należy zmodyfikować instrukcję wyjścia
disp(‘Sumą dwóch liczb jest’,z) w której z traktowana jest jako liczba
na instrukcję
disp(‘Sumą dwóch liczb jest  ‘+string(z)) w której z traktowane jak jako łańcuch znaków, czyli tekst.
Zauważ, że na końcu ‘Sumą dwóch liczb jest  ‘
jest spacja. Będzie ładniej
Program P4-3

clear;clc;
x=input('wprowadź pierwszą liczbę ')
y=input('wprowadź drugą liczbę ')
z=x+y
disp('Sumą dwóch liczb jest '+string(z))

Wykonaj samodzielnie ten program. Pamiętaj, żeby przed wykonaniem program zapisać! 
Po wykonaniu otrzymasz coś takiego.

wprowadź pierwszą liczbę 3
wprowadź drugą liczbę 4
“Sumą dwóch liczb jest 7”  

Rozdział 4.4 Instrukcje związane z wykresami funkcji dwuwymiarowymi czyli 2D
Rozdział 4.4.1 Wykres ciągły
Mamy 2 wektory x i y i chcemy zrobić wykres y=f(x)
Nic prostszego.
Wystarczy wykonać w Scilabie poniższy program
Program P4-4

clc;clear;
x=[1,2,3,4,5,6,7,8,9,10]
y=[1,4,9,16,25,36,49,64,81,100]
plot(x,y)

Instrukcja plot(x,y) połączy liniami prostymi punkty o współrzędnych x,y.

Rys.4-3
Wykres  ciągły plot(x,y)
Pamiętaj, żeby przed wykonaniem zapisać go. Jak zwykle nadpiszemy go na poprzednim pliku. Wykonaj bez echa. Na końcu zamknij okno wykresu. Po co? Żeby ew. następne wykresy nie były nadpisywane.
Uwaga:
Wykres wygląda na ciągły. Ale jak się dobrze przyjrzysz, to połączył punkty o współrzędnych (1,1),(2,4)…(10,100) odcinkami prostymi!

Rozdział 4.4.2 Wykres punktowy
A co będzie gdy instrukcję plot(x,y) zastąpimy plot(x,y,’o’) ?
Powstanie wtedy tzw. wykres punktowy.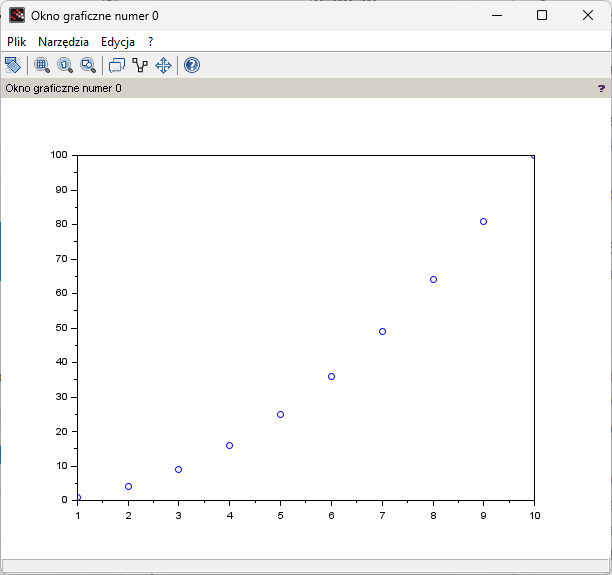 

Rys.4-4
Wykres  punktowy plot(x,y,’o’)
Rozdział 4.4.3 A jak wykonać wykres dowolnej funkcji?
Zaczynamy od przedszkola, czyli wykresu y=x²

Program P4-5

clc;clear;
x=[-5:0.1:5]
y=x.^2//zwróć uwagę na kropkę przy x!
plot(x,y)

Instrukcja x=[-5:0.1:5] wyznacza dziedzinę funkcji y=x². Dla matematyka jest to funkcja ciągła dla x=-5…+5. W praktyce jest to wykres “gęsto punktowy” w zakresie x=-5…+5 w odstępach co Δx =0.1 czyli dla x=-5,-4.9,-4.8….0…+4.8,+4.9,+5.
Uwaga
Instrukcję x=[-5:0.1;5] można też użyć w innej wersji x=linspace(-5,+5,100). Czyli wykonaj wykres dla 100 równo rozłożonych zmiennych x w zakresie x=-5…+5.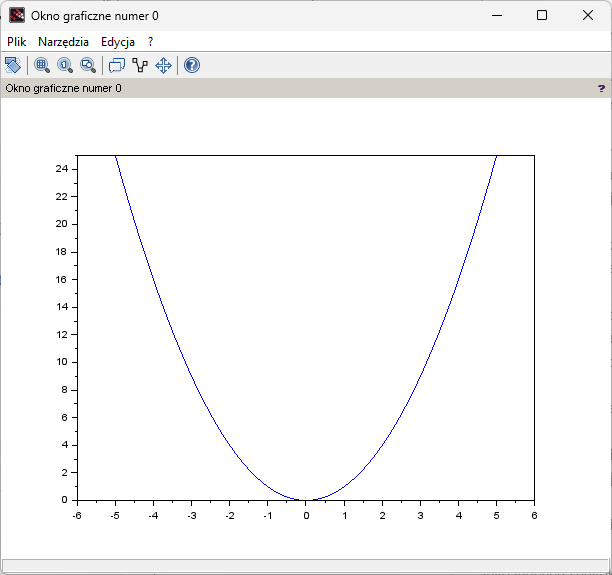

Rys. 4-5
Wykres y=x²
Chociaż formalnie jest to wykres punktowy, to ze względu na odstępy Δx=0.1, czyli dużą gęstość, jest to praktycznie wykres ciągły. 
Spróbuj poeksperymentować z instrukcją plot(x,y)
Np. plot(x,y,’–‘) da coś takiego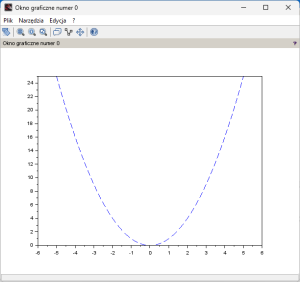

Rys.4-6
Wykres y=x² w wersji przerywanej.
A kolory wykresu robimy tak
plot(x,y) jako “default” kolor niebieski
plot(x,y,’r’) kolor czerwony
plot(x,y,’g’) kolor zielony
plot(x,y,’y’) kolor żółty
Proponuję poeksperymentować. Inne kolory znajdziesz w “Help”-ie, lub w innych kursach Scilaba.
Rozdział 4.4.4 Teksty na wykresie
Każdy porządny wykres musi być jakoś opisany

Program P4-6

clc;clear;
x=[-5:0.1:+5]
y=x.^2
plot(x,y)
xgrid
legend(['Funkcja kwadratowa'])
xtitle('Wykresy funkcji','oś x','oś y')

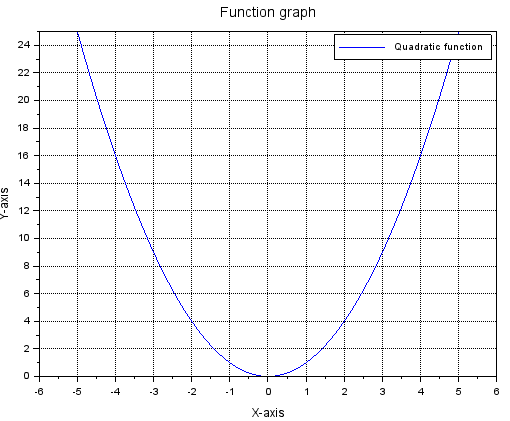
Rys.4-7
Wykres y=x² w wersji “Full wypas”
– Instrukcja xgrid w wersji podstawowej dodała siatkę. Może też zawierać dodatkowe parametry dotyczące samej siatki.
– Instrukcja legend([‘Funkcja kwadratowa’])  opisuje wykres funkcji. Miałaby  większe  znaczenie gdyby na wykresie było kilka wykresów
– Instrukcja xtitle(‘Wykresy funkcji’,’oś x’,’oś y’) opisuje wykres oraz jego osie
* Instrukcja xgrid jest tu w wersji podstawowej. 
Scilab umożliwia rysowanie wykresów 2D w dowolnych konfiguracjach. Bez problemu na jednym wykresie można umieścić kilka funkcji. Np. Funkcję kwadratową i sześcienną. Może też umieścić na jednym rysunku kilka wykresów z których każdy zawiera kilka funkcji. 
Rozdział 4.5 Wykresy trójwymiarowe
Tylko wspomnę, że są takie możliwości. Przy okazji poznasz jak korzystać z przykładowych programów Scilaba. 

Rys.4-8
z=sin(x)*sin(y) jako przykład programu 3D 
Dla x=-4…+4 oraz  y=-4…+4
Na początku szukasz tego programu klikając w oknie konsoli ikonkę “Przykłady”.
Klikając prawą myszką w róg wykresu, możesz go oglądać pod dowolnym kątem.
Spróbuj samemu obejrzeć ten program w Scilabie. Inne też