Podstawy automatyki

Rozdz. 24 Regulacja PD

Rozdz. 24.1 Wstęp
Regulator typu PD należy do grupy regulatorów PID. Wyłączono w nim tylko akcję całkowania I. Ma on niestety podstawową wadę regulatora P. Nie eliminuje całkowicie uchybu w stanie ustalonym. Wzmocnienie układu zamkniętego Kz i wzmocnienie uchybowe Ke w stanie ustalonym Ke też są takie same jak dla regulacji typu P:

Rys. 24-1
Wróć na koniec poprzedniego rozdziału, to będziesz wiedział dlaczego. A to oznacza że np. dla K=100 uchyb ustalony wynosi ok. 1%. To w czym w takim razie PD jest lepsze od P? Poprawia stabilność i skraca czas regulacji! Dla regulatora P stabilność i mały uchyb w stanie ustalonym są ze sobą w sprzeczności. Duże Kp zapewnia mały uchyb ustalony, ale zwiększają się oscylacje i czas regulacji. Układ może nawet stać się niestabilnym. Spójrz na typowe sterowanie typu P.

Taką odpowiedź układu regulacji P otrzymałeś w poprzednim rozdziale (Rys. 23-9). Co by tu zrobić, żeby były mniejsze oscylacje? Pierwsza genialna myśl-zmniejszyć Kp regulatora. Np Kp=5. Super, oscylacje będą mniejsze. Za to uchyb ustalony będzie 2 razy większy. Nie idź tą drogą. Nie ruszajmy więc Kp, ale kombinujmy. Oscylacje są dlatego, że na początku skoku x(t) sygnał y(t) zbyt szybko rośnie. W ten sposób rozpędzone „wahadło” y(t) przechodzi na „drugą stronę”. A gdyby powstrzymywać wahadło w czasie rozpędzania hamowaniem proporcjonalnym do jego prędkości? Podobnie działają samochodowe tłumiki hydrauliczne. Może wtedy nie przejdzie na „drugą stronę”. Albo „tylko trochę”? W końcu y(t) się ustali. Wtedy Kz i Ke wstanie ustalonym będą zgodne z Rys. 24-1. Bo człon różniczkujący w stanie ustalonym daje zero. Tak jakby był wyłączony! W ten sposób dochodzimy do jakiegoś sterowania, które zależy także od prędkości sygnału! Czyli pojawi się człon różniczkujący
Przypomnijmy sobie podstawowe własności tego członu, zwanego D–>Differential-Różniczkujący.

Rozdz. 24.2 Badanie idealnego członu różniczkującego D i rzeczywistego różniczkującego D
Rozdz. 24.2.1 Wstęp
Zbadamy odpowiedź na skok i na sygnał narastający liniowo. Po co to drugie? Bo skok daje w członie różniczkującym trudny do zmierzenia impuls Diraca.
Rozdz. 24.2.2 Odpowiedź Idealnego członu różniczkującego na skok

Rys. 24-3
Zróżniczkowany został skok jednostkowy x(t). W rezultacie otrzymaliśmy odpowiedź y(t) typu „młotek” diraca. Przypominam, że człon różniczkujący „oblicza” prędkość sygnału x(t). A jaka jest prędkość sygnału x(t). Dla t<1sek x(t)=0 i dla t>1sek x(t)=1. Dla tych t sygnał x(t) jest stały. Czyli y(t)= prędkość x(t) jest zerowa. Dlatego y(t)=0, co widać na załączonym obrazku.
A jaka jest prędkość y(t) dla t=1? Nieskończenie wielka! Summa sumarum wyjście y(t) jest impulsem Diraca.
W regulacji staramy się unikać się idealnych członów różniczkujących. Są one bardzo wrażliwe na zakłócenia, zwłaszcza na szybkie zmiany, czyli np. na zakłócenia elektromagnetyczne. Stosuje się raczej tzw człony różniczkujące rzeczywiste.
Rozdz. 24.2.3 Odpowiedź rzeczywistego członu różniczkującego na skok

Rys. 24-4
Do członu różniczkującego idealnego został dodany szeregowo człon inercyjny o stałej czasowej T=0.1 sek. Tłumi on skok jednostkowy, zanim wejdzie na idealny człon różniczkujący. Otrzymaliśmy coś podobnego do impulsu Diraca. Jego wysokość już nie jest nieskończona, tylko ma wartość y(t)=10. Kojarzysz to jakoś ze stałą czasową T=0.1sek? Chyba tak, jest to odwrotność 0.1. Skok jednostkowy x(t) daje trochę dziwną, trudną do zmierzenia odpowiedź. Zwłaszcza dla członu idealnego różniczkującego. Dlatego do ich badania lepiej nadaje się liniowo narastający sygnał wejściowy x(t). Inna nazwa to piła, rampa….
Rozdz. 27.2.4 Odpowiedź idealnego członu różniczkującego na sygnał narastający liniowo

Rys. 24-5
Człon różniczkujący, jak sama nazwa wskazuje, różniczkuje sygnał x(t) dając y(t). Dla np. studentów teksty na rysunku są trywialne. Natomiast dla mających problem z rachunkiem różniczkowym niech wystarczy, że dla członu różniczkującego czerwone y(t) jest prędkością czarnego x(t). Widać wyraźnie, że w 5 sekundzie prędkość sygnału x(t) wzrosła dwukrotnie. Dlatego czerwone y(t) jako pochodna x(t) też wzrosła dwukrotnie.
Rozdz. 24.2.5 Odpowiedź rzeczywistego członu różniczkującego na sygnał narastający liniowo

Rys. 24-6
Tego się spodziewaliśmy. Tam gdzie prędkość się nie zmienia, np. po 2 i 6 sekundzie, obliczana jest ona jako stała  0.5/sek i 1/sek. Natomiast gdy się zmienia (w 1 i 5 sekundzie), to człon rzeczywisty potrzebuje trochę czasu, żeby ją obliczyć. To może być pewną, choć nie decydującą wadą. Za to zaletą będzie odporność na zakłócenia typu „szybka zmiana”. Będą one po prostu tłumione przez człon inercyjny.
Dalej będziemy badać człony PD , które są równoległym połączeniem członu proporcjonalnego i różniczkującego (idealnego lub rzeczywistego). Nie są jeszcze regulatorami, bo wejściem jest tylko pojedynczy sygnał x(t) a nie uchyb e(t)=x(t)-y(t)

Rozdz. 24.3 Badanie idealnego członu PD i rzeczywistego PD
Wstęp 24.3.1
Też zbadamy odpowiedź na skok i na sygnał narastający liniowo.
Rozdz. 24.3.2 Odpowiedź idealnego członu PD na skok
Pamiętaj !
Człon PD to jeszcze nie regulator! Nie ma on elementu porównującego obliczającego uchyb e(t)=x(t)-y(t). Dotyczy także rzeczywistego PD.

Rys. 24-7
W pierwszej chwili przebieg jest podobny do Rys. 24-3. Dopiero jak się dobrze przyjrzysz, to się okaże, że pojawia się składowa proporcjonalna y(t)=1. Dla członu różniczkującego idealnego z Rys. 24-3, ta składowa była zerowa.
Rozdz. 24.3.3 Odpowiedź rzeczywistego członu PD na skok
Czym różni się od idealnego PD? Porównaj z Rys. 24-7.

Rys. 24-8
Widać składową proporcjonalną (skok jednostkowy w 3 sekundzie) i składową różniczkującą rzeczywistą („rozciągnięty” pik o wysokości 10=11-1) Zbadajmy teraz odpowiedź na liniowy sygnał narastający, która lepiej oddaje charakter członu PD niż odpowiedź na skok.
Rozdz. 24.3.4 Odpowiedź idealnego członu PD na sygnał narastający liniowo

Rys. 24-9
Wymuszeniem x(t) jest sygnał narastający liniowo, który w 5 sekundzie dwukrotnie zwiększa prędkość narastania. W odpowiedzi y(t) widać składową różniczkującą D i proporcjonalną P. Akurat tylko w tym przypadku, gdy Kp=1, Td=1sek, składowa P idealnie pokrywa się z wymuszeniem x(t). Przy okazji widzisz definicje czasu różniczkowania Td. Jest to czas t=1sek, w którym składowa proporcjonalna P zrówna się ze składową różniczkującą D.
Rozdz. 24.3.5 Odpowiedź rzeczywistego członu PD na sygnał narastający liniowo

Rys. 24-10
Odpowiedź podobna do członu idealnego PD. „Wygładzenia” po 1 i 5 sekundzie (wtedy występuje zmiana prędkości sygnału x(t)) wynikają z tego, że tor różniczkujący rzeczywisty potrzebuje ok. 0.5 sek żeby „dojść do siebie” i obliczyć właściwą prędkość. Wstanie ustalonym dobrze widać składową proporcjonalną P i D która jest taka sama jak dla idealnego członu PD. Podkreślam-taka sama ale tylko w stanie ustalonym.

Rozdz. 24.4 Regulator PD z obiektem dwuinercyjnym
Rozdz. 24.4.1 Wstęp
Będziemy badać układ regulacji z obiektem dwuinercyjnym, a następnie w rozdz. 27.7 z trójinercyjnym.
Zaraz, zaraz. A dlaczego nie zaczynamy od jednoinercyjnego? Dlatego, że do sterowania tym obiektem wystarczy regulacja P z rozdz. 26.
Tu można udowodnić, np. z kryterium Hurwitza, że dla dowolnie dużego wzmocnienia, nawet dla Kp=1 000 000 układ będzie zawsze stabilny. Mało tego, nie ma żadnych oscylacji, a odpowiedź będzie prawie skokiem.
Dla pozostałych obiektów dynamicznych, dodanie do regulatora proporcjonalnego członu różniczkującego D szokująco poprawie odpowiedź. Mogą zniknąć oscylacje, a układ który przy regulatorze typu P był niestabilnym, może stać się stabilnym.
Uwaga.
Tak naprawdę, to będziemy badać rzeczywisty a nie idealny regulator PD. Tzn. w regulatorze PD zamiast członu różniczkującego idealnego D będzie człon różniczkujący rzeczywisty D. Da on odpowiedź proporcjonalną do prędkości sygnału wejściowego, która obliczona jest z pewną inercją. Patrz Rys. 27-18. Taka struktura zmniejszy zakłócenia od sygnałów szybkozmiennych, które są typowe dla idealnego członu D.
Najpierw zbadajmy sam obiekt dwuinercyjny. Robiłeś to w rozdziale 26 w p.26.4.2.
Rozdz. 24.4.2 Badanie obiektu dwuinercyjnego

Rys. 24-11
Typowa odpowiedź obiektu wieloinercyjnego , tu dwuinercyjnego. Dalej będziemy badać regulację PD z tym obiektem przy Kp=10 i czterema różnymi nastawami różniczkowania-Td= 0, 1, 5 i 20 sek. Jakie Td zapewni nam najlepszą odpowiedź z możliwie małymi oscylacjami i krótkim czasem regulacji?
Rozdz. 24.4.3 Regulacja PD Kp=10 Td=0 sek
Td=0 oznacza, że wyłączone jest różniczkowanie (rzeczywiste) D. Czyli mamy typową regulację typu P

Rys. 24-12
Kp=10 Td=0
Czyli jest to regulacja P z Rys.23-9 z poprzedniego rozdziału. Wzmocnienie w stanie ustalonym Kz=y/x=0.91/1=0.91 jest zgodne z wykresem i z teorią .
Rozdz. 24.4.4 Regulacja PD Kp=10 Td=1 sek
Oscylacje na Rys. 24-12 trochę irytują. Wprowadźmy więc do boju składową różniczkującą D. Najpierw ostrożnie, małe rózniczkowanie . Np.Td=1 sek. Przypominam, że cały czas mamy z członem różniczkującym rzeczywistym a nie idealnym! Dlaczego? Wyjaśniłem wcześniej. I tak już dalej będzie.
Czym się różni poniższy regulator  PD od członu PD z np. Rys. 24-8? Oprócz innej nastawy Kp oczywiście. Tylko tym, że sygnałem wejściowym jest uchyb e(t)=x(t)-y(t) a nie pojedyncze x(t). Pojawia się tu najważniejszy element regulatora, element porównujący wartość zadaną x(t) z sygnałem wyjściowym y(t). Jest on nawet ważniejszy niż pozostała część obliczeniowa regulatora – człony P i D. Bo można sobie wyobrazić regulator składający się tylko z elementu porównującego obliczającego uchyb e(t)=x(t)-y(t). Jest to po prostu regulator P o nastawie Kp=1. Natomiast regulator bez elementu porównującego jest bez sensu.

Rys. 24-13
Kp=10 Td=1 sek
A nie mówiłem, że PD poprawia własności dynamiczne? Porównaj tylko z Rys. 24-12 gdzie nie było składowej D. Oscylacje i czas regulacji są radykalnie mniejsze. A to było tylko małe różniczkowanie Td=1sek. To co to będzie, gdy Td zwiększymy np. na Td=5 sek? Dowiesz się o tym za chwilę. Co do własności statycznych, to stan ustalony y(t)=0.91 jest taki sam jak dla regulacji typu P z Rys. 24-12. Jest to oczywiste, bo w stanie ustalonym różniczkowanie D daje wyjście zerowe, czyli nie ma wpływu na sterowanie.
Jak uzasadnić lepsze własności dynamiczne? Inaczej, ładniejsze dochodzenie y(t) do wartości zadanej 0.91 Najłatwiej to “Tako rzecze Królowa Nauk – Matematyka. Dokładnie to analiza matematyczna.
A na chłopski rozum?
1-Stan ustalony jest taki sam, jak dla regulacji P z Rys. 24-12.
2-Prędkość narastania y(t) w pierwszej sekundzie skoku jest większa, bo dochodzi różniczkowanie przedniego zbocza x(t), które „podbija” sygnał sterujący s(t). Na Rys. 24-14 będziesz badał ten sam układ, tylko z innymi nastawami oscyloskopu, dającym widok całego s(t), a nie „uciętego” na poziomie 2 jak na rysunku .
Okaże się, że dla t=3 (początek skoku) sygnał sterujący s(t)=110=100+10!, gdzie 10 to składowa P a 100 to składowa D. Czyli PD da na początku skoku x(t) kopa w górę 11 razy większego od regulatora P! To powinno spowodować szybsze dojście do stanu ustalonego 0.91. Już nie wspomnę, że ten kop jest 110 razy większy niż w układzie otwartym, czyli bez regulatora.
3-No dobrze, regulator PD dał na początku skoku x(t) potężnego kopa w górę. W takim razie powinniśmy się tym bardziej spodziewać dużych przeregulowań, większych niż ymax=1,2 w regulacji P na Rys. 24-12. A tu jest akurat odwrotnie, malutkie przeregulowanie ymax=1 po 5 sekundzie.
Jak to wytłumaczyć?
Okazuje się, że składowa D nie tylko „popędza” obiekt na początku skoku x(t), ale potem go „hamuje”. Zauważ, że przeważająca w sygnale sterującym na początku składowa D od x(t) po pewnym czasie dość szybko znika do zera. Widać to np. na Rys. 27-14. Za to pojawia się składowa D od y(t) pełniąca rolę „hamulcowego”.
Na początku ta składowa jest największa, bo prędkość y(t) jest największa. Potem gdy y(t) się ustali to ona też zniknie. Ale znaczniej później niż składowa D od x(t)! I najważniejsze. Składowa D od y(t) odejmuje się od składowej D od x(t) stąd hamowanie. Bo tak działa element porównawczy – e(t)=x(t)-y(t). I to jak jak hamuje niebieski sygnał sterujący s(t)! Przecież s(t) chwilami mrozi ujemną temperaturą, chociaż wartością zadaną jest x(t)=+100°C! Ale dzięki temu system jest bardzo dynamiczny i szybko dochodzi do stanu ustalonego.
Różniczkowanie y(t) stara się zapobiegać przeregulowaniom. Dlatego przebiegi regulacji PD szybciej dochodzą do stanu ustalonego i z mniejszymi oscylacjami.
Regulacja PD nie powstała jako efekt teoretycznych rozważań bardzo mądrych ludzi. Szermierz musi trafić w określone miejsce przeciwnika. Nie musi tego zrobić z absolutną dokładnością np. co do milimetra. Wystarczy, że zrobi to dokładnością  5 cm ale szybko! Kieruje się więc nie tylko położeniem celu, ale także także   prędkością zmiany położenia tego celu. Umiejętność tą nabywa podświadomie wieloletnimi treningami, stopniowo optymalizując nastawy swego prywatnego regulatora PD. Zauważ, że nie jest tu wymagany uchyb zerowy czyli absolutna celność trafień.
Pokażę jeszcze raz ten sam przebieg, co na Rys. 27-24 z takimi nastawami oscyloskopu, żeby był widoczny cały sygnał sterujący s(t).

Rys. 24-14
Widać że s(t)=110! Za to y(t)=0.91 w stanie ustalonym, jest prawie przy osi czasu. Wykres pokazuje nam jak duże może być s(t). Przebiegi są dokładnie takie same jak na Rys. 24-14, tylko w innej skali.
Podsumowanie
PD na początku daje duży sygnał sterujący głównie od różniczkowania skoku x(t) po to, żeby y(t) szybciej doszło do stanu ustalonego. Potem hamuje sygnałem różniczkującym od y(t), po to żeby zmniejszyć efekt wahadła, czyli zmniejszyć oscylacje. W wyniku dostajemy taki przebieg y(t), który jest wyraźnie lepszy od regulacji P z Rys. 24-12.
A gdyby tak jeszcze zwiększyć intensywność różniczkowania. Np. Td=5 sek
Rozdz. 24.4.5 Regulacja PD Kp=10 Td=5 sek

Rys. 24-15
Kp=10 Td=5 sek
Różniczkowanie jest teraz 5 razy mocniejsze! Wydawałoby się, że już lepiej niż na Rys 24-14 być nie może. A tu taki przebieg. Czerwone y(t) to prawie prostokątne x(t)! Porównaj z czerwonym y(t) z Rys. 24-12 regulacji PD, w którym Td=0, czyli z regulacją typu P. Niebo a ziemia. “Ucięty” przez oscyloskop sygnał s(t) ma w 3 sekundzie wartość smax=510! To idźmy na całość i dajmy Td=20 sek. Może y(t) jeszcze jeszcze lepsze, czytaj-bardziej się „sprostokąci”?
Rozdz. 24.4.6 Regulacja PD Kp=10 Td=20 sek

Rys. 24-16
Kp=10 Td=20 sek
Przesadziliśmy z różniczkowaniem. Co za dużo, to nie zdrowo. Nie dość, że powstały oscylacje, to potem układ dochodzi do stanu ustalonego y=0.91 dopiero po ok. 50 sek. A s(t) w 3 sek ma wartość aż 2010! To wolne dochodzenie do stanu ustalonego można wytłumaczyć zbyt silnym hamowaniem sygnału D pochodzącego od różniczkowania y(t).
Rozdz. 24.4.7 Regulacja PD Kp=100 Td=0 sek
Nastawy Kp=10 i D=5 sek z Rys. 24-15 dały nam szybką odpowiedź, z ledwo widocznym początkiem jednej oscylacji. Tylko sygnał ustalony y(t)=0.91 zbyt odbiega od wartości zadanej x(t)=1. Rzeczywiście uchyb ustalony e(t)=1-0.91=0.09 chwały wiekopomnej nie przynosi. Aby go zmniejszyć, zwiększymy wzmocnienie na Kp=100. Będziemy więc badać regulację PD z obiektem dwuinercyjnym z Kp=100 i czterema różnymi Td = 0, 0.25, 2 i 5 sek. Zaczniemy jak zwykle od Td=0, czyli od regulacji P (bez różniczkowania).

Rys. 24-17
Kp=100 Td=0  oznacza, że wyłączone jest różniczkowanie D. Czyli mamy typowa regulację typu P. Powtarzamy eksperyment z Rys. 23-11 z poprzedniego rozdziału
Uwaga.
W poprzednich przebiegach sygnał sterujący s(t) był linią niebieską. Kolor ten jest jednak dość dominujący i często zamulał rysunek, czego jaskrawym przykładem był np. Rys. 24-16. Dlatego sygnałowi s(t) przyporządkujemy kolor żółty.
Sygnał wyjściowy y(t) zgodnie z teorią osiągnął wartość ustaloną 0.99 a uchyb ustalony e(t) wartość 0.01. Za to oscylacje i długi czas dochodzenia do równowagi są nie do zaakceptowania.
Spodziewamy się, że znowu pomoże składowa różniczkująca D. Jak zwykle zaczniemy ostrożnie od małego Td=0.25sek.
Rozdz. 24.4.8 Regulacja PD Kp=100 Td=0.25 sek

Rys. 24-18
Kp=100 Td=0.25 sek
Jest znacznie szybsze i mniej „oscylacyjne” dojście do stanu ustalonego y(t)=0.99 (i oczywiście uchybu ustalonego e(t)=0.01) niż dla regulacji P (bo Td=0) z Rys. 24-17. A może da się lepiej?
Rozdz. 24.4.9 Regulacja PD Kp=100 Td=2 sek

Rys. 24-19
Kp=100 Td=2 sek
Samo y(t) ma małą oscylacje. Za to sygnał sterujący to ho, ho! Jest to typowe, że oscylacje sygnału sterującego s(t) są dużo większe niż y(t). Nawet gdy wydaje się, że y(t) już śpi, s(t) jeszcze wykonuje jakieś ruchy „wte i we wte”. Odpowiedź jest lepsza niż dla Td=0.25 sek z Rys. 24-18. To zwiększmy jeszcze Td?
Rozdz. 24.4.10 Regulacja PD Kp=100 Td=5 sek

Rys. 24-20
Kp=100 Td=5 sek
Przesadziliśmy z różniczkowaniem. Oscylacje i czas regulacji są większe.
Rozdz. 24.4.11 Wnioski ze sterowania PD obiektem dwuinercyjnym
1 – Uchyb ustalony dla Kp=10 to 0.09% a dla Kp=100 to 0.01% i nie zależy od Td. Czyli ze wzrostem Kp maleje uchyb ustalony e(t).
W stanie ustalonym y(t)=0.99 i e(t)=0.01.
2– Dla pewnego optymalnego Td składowa różniczkująca radykalnie skraca czas regulacji i zmniejsza oscylacje. Dla każdego wzmocnienia Kp istnieje optymalne Td dla którego odpowiedź jest optymalna. Czyli z małymi oscylacjami (nawet bez) i z krótkim czasem regulacji. Stwierdziliśmy, że dla Kp=10 optymalne jest Td=5 sek a dla Kp=100 Td=2 sek. Na pewno są lepsze nastawy, bo robiliśmy tylko kilka doświadczeń.
3– Można udowodnić np. z kryterium Hurwitza lub Nyquista, że dla dowolnego Kp regulacja z członem dwuinercyjnym jest zawsze stabilna. Inna rzecz, że mogą wtedy pojawić się oscylacje o dużej amplitudzie i długim czasem trwania.

Rozdz. 24.5 Regulator PD z obiektem trójinercyjnym
Rozdz. 24.5.1 Wstęp
Zrobimy to samo, co z dwuinercyjnym. Spodziewamy się większych kłopotów. Rzeczywiście, czas regulacji i oscylacje będą większe. Mało tego, przy pewnym wzmocnieniu układ stanie się niestabilny. Będziemy badać sterowanie dla wzmocnienia Kp=10 i Kp=25 przy różnych Td. Przy Kp=25 uchyb będzie oczywiście mniejszy, ale przy pewnych Td układ stanie się niestabilny! Tego nie było w dwuinercyjnym.
Zaczniemy od gołego obiektu.
Rozdz. 24.5.2 Badanie obiektu trójinercyjnego

Rys. 24-21
Bez komentarza
W następnych punktach będziemy badać regulację PD obiektu Trójinercyjnego z Kp=10 i Kp=25 z różnymi nastawami Td.
Jakie Kp i Td zapewni najlepszą odpowiedź?
Rozdz. 24.5.3 Regulacja PD Kp=10 Td=0 sek
Td=0 oznacza, że mamy regulację typu P. Powtarzamy więc eksperyment z poprzedniego rozdziału Rys. 23-13.

Rys. 24-22
Kp=10 Td=0 czyli regulacja typu P
Przebieg z wieloma oscylacjami i długim czasem regulacji. Czyli regulacja P nie sprawdza się dla tego obiektu. Wzmocnienie w stanie ustalonym Kz=0.91, czyli y(t)=0.91 w stanie ustalonym, jest zgodne z wykresem i z teorią.
Rozdz. 24.5.4 Regulacja PD Kp=10 Td=0.5 sek
Zaczynamy ostrożnie z małym różniczkowaniem Td=0.5 sek.

Rys. 24-23
Kp=10 Td=0.5 sek
Dużo lepiej niż bez składowej różniczkującej z Rys. 24-22. To zwiększmy Td na 1.5 sek. Może będzie jeszcze fajniej.
Rozdz. 24.5.5 Regulacja PD Kp=10 Td=1.5 sek

Rys. 24-24
Kp=10 Td=1.5 sek
Jest fajniej. Przebieg wyraźnie lepszy od Rys. 24-23,a tym bardziej od Rys. 24-22. A może da się go jeszcze poprawić? Np. dla Td=5sek
Rozdz. 24.5.6 Regulacja PD Kp=10 Td=5 sek

Rys. 24-25
Kp=10 Td=5 sek
Gorzej niż dla Td=1.5 sek. Większa amplituda y(t) i więcej oscylacji. Można przypuszczać, że dalsze zwiększanie Td  pogorszy tylko sytuację.
Wnioski dla Kp=10.
Wyraźnie widać, że obiekt jest trudniejszy do sterowania od dwuinercyjnego. Optymalnym parametrem różniczkowania jest Td=1.5 sek. Trochę drażni duży uchyb ustalony 0.09. Dlatego spróbujmy zwiększyć wzmocnienie na Kp=25. Na więcej to raczej nie. Obawiam się niestabilności.
Rozdz. 24.5.7 Regulacja PD Kp=25 Td=0
Wyłączyłem różniczkowanie dając Td=0. Czyli jak zwykle zaczynamy od regulacji P.

Rys. 24-26
Kp=25 Td=0
Układ stał się niestabilny i przy takim wzmocnieniu oscyloskopu lepiej widać narastająca sinusoidę y(t). Po co podałem wzór na wzmocnienie w stanie ustalonym Kz? Czy on ma sens, gdy system jest niestabilny? Trochę ma. Tu Kz=0.96 to składowa stała tej sinusoidy y(t). Gdybyś powiększył wzmocnienie oscyloskopu, to nawet dałoby się to zauważyć. Wprowadźmy ostrożnie nieduże różniczkowanie.–> Td=0.5 sek. Może to ustabilizuje ukłasd?
Rozdz. 24.5.8 Regulacja PD Kp=25 Td=0.5 sek

Rys.26-27
Kp=25 Td=0.5 sek
Tu widać cudowny wpływ składowej różniczkującej D. Układ stał się stabilny!
Może trochę za dużo oscylacji. A gdyby tak dać Td=1sek?
Rozdz. 27.5.9 Regulacja PD Kp=25 Td=1 sek

Rys. 24-28
Kp=25 Td=1 sek.
Chyba lepszy przebieg. To dalej szukajmy szczęścia , może Td=5 sek?
Rozdz. 24.5.10 Regulacja PD Kp=25 Td=5 sek

Rys. 24-29
Kp=25 Td=5 sek.
Przedobrzyliśmy. Nie do zaakceptowania.

Rozdz. 24.6 Regulacja PD z zakłóceniami
24.6.1 Wstęp
Sterowane będą te same 2 obiekty co poprzednio: dwuinercyjny i trójinercyjny. Na ich wejścia będzie podawany dodatkowo (oprócz sygnału sterującego s(t) z regulatora PD), sygnał zakłócający z(t)=+0.5 lub z(t)=-0.5. Są to potężne zakłócenia! Trudno sobie wyobrazić, że sieć skacze z 230 V na 345 V lub na 135 V.
Specjalnie podałem taką karykaturę sieci, po to by pokazać główny cel regulacji – tłumienie zakłóceń. Często jest to ważniejsze niż ładne dojście do wartości zadanej x(t). Jak masz lodówkę to wiesz dlaczego. Wartość zadaną temperatury w lodówce zmienia się rzadko (często przez całe życie masz ją ustawioną przez fabrykę), a zakłócenia występują bez przerwy. Przy zakłóceniach wybraliśmy takie nastawy wyznaczone przez nas wcześniej Kp i Td, dla których odpowiedź na x(t) była optymalna. Inaczej „najładniejsza”.
Uwaga
Zwróć uwagę na to, że odpowiedź na skok x(t) będzie znacznie szybsza niż reakcja na zakłócenie z(t). Czyli transmitancje G(s) („główna?”) i zakłóceniowa Gz(s) są różne. Wynika z tego ważny wniosek. Projektując układ w którym wiesz, że wartość zadana zmienia się rzadko, należy kierować się raczej optymalną transmitancją zakłóceniową Gzakl(s).
Rozdz. 24.6.2 Zakłócenie dodatnie na dwuinercyjny z(t)=+0.5, Kp=10 D Td=5
Zakłócenie z(t)=+0.5 pojawi się w 30 sekundzie.

Rys. 24-30
Do 30 sekundy, czyli do pojawienia się zakłócenia, przebieg jest z oczywistych powodów taki sam jak na Rys. 24-13. Zakłócenie z(t)=+0.5 spowodowało wzrost y(t) do +0.95. Zakłócenie nie zostało więc całkowicie stłumione. Taka jest niestety uroda regulacji P lub PD. Ale bez regulacji, czyli w układzie otwartym, sygnał y(t) skoczyłby z 1.0 na 1.5!
Zauważ że odpowiedź na skok jest szybka a na zakłócenie wolna.
Bo transmitancja zakłóceniowa Gzakl(s) jest inna niż układu zamkniętego Gz(s)!
Wniosek
Gdy wartość zadana x(t) zmienia się rzadko, to dobieraj nastawy regulatora ze względu na zakłócenie z(t)
Gdy wartość zadana x(t) zmienia się często, to dobieraj nastawy regulatora ze względu na wartość zadaną x(t)
Rozdz. 24.6.3 Zakłócenie ujemne na dwuinercyjny z(t)=-0.5, Kp=10 D Td=5
Zakłócenie z(t)=-0.5 pojawi się w 30 sekundzie.

Rys. 24-31
Zakłócenie z(t)=-0.5 spowodowało spadek y(t) do 0.86. Zauważ, że sygnał sterujący s(t) stara się skompensować zakłócenie z(t), działając w przeciwnym kierunku, niż zakłócenie.
Tak działa każdy dobrze zaprojektowany układ regulacji!
Rozdz. 24.6.4 Zakłócenie dodatnie na dwuinercyjny z(t)=+0.5, Kp=100 D Td=2

Rys. 24-32
Zakłócenie z(t)=+0.5 pojawi się w 30 sekundzie.
Zakłócenie z(t)=+0.5 spowodowało wzrost y(t) do 0.995. Prawie nie widać wpływu zakłócenia! Zostało prawie skompensowane spadkiem żółtego sygnału sterującego s(t).
Uwaga
Sygnały ustalone przed zakłóceniem z(t) i po z(t)
e(t)=0.01 i e(t)=0.005 leżą blisko e(t)=0
oraz
y(t)=0.99 i y(t)=0.995 leżą blisko x(t)=1
Dlatego podałem ich wartości przybliżone.
Efekt ten jest bardziej widoczny na Rys. 24-30 gdy wzmocnienie Kp regulatora jest mniejsze tzn. Kp=10.
Rozdz. 24.6.5 Zakłócenie ujemne na dwuinercyjny z(t)=-0.5, Kp=100 D Td=5
Zakłócenie z(t)=-0.5 pojawi się w 30 sekundzie.

Rys. 24-33
Zakłócenie z(t)=-0.5 spowodowało spadek y(t) do 0.985. Też ledwo widoczny wpływ zakłócenia. Porównaj z Rys.24-31 gdy Kp=10.
Rozdz. 24.6.6 Zakłócenie dodatnie na trójinercyjny z(t)=+0.5, Kp=10 Td=1.5 sek
Zakłócenie z(t)=+0.5 pojawi się w 30 sekundzie.

Rys. 24-34
Porównaj z Rys. 24-30. Już chciałem napisać że układ wolniej reaguje na x(t) i zakłócenia, a tu okazuje się że owszem. Na skok wartości zadanej reaguje wolniej, ale na zakłócenie z(t) szybciej! A przecież obiekt trójinercyjny jest trudniejszy do sterowania niż dwuinercyjny! Zgoda, ale jak już wiemy wiemy, optymalna nastawa Td dla skoku x(t), może być nieoptymalna dla zakłócenia z(t) i odwrotnie. Dla obiektu dwuinercyjnego i dla Td mniejszego niż 5 sek , odpowiedź na z(t) będzie szybsza (czytaj – lepsza), za to odpowiedź na x(t) będzie bardziej oscylacyjna (czytaj – gorsza).
Rozdz. 24.6.7 Zakłócenie ujemne na trójinercyjny z(t)=-0.5, Kp=10 Td=1.5 sek
Zakłócenie z(t)=-0.5 pojawi się w 30 sekundzie.

Rys. 24-35
Na zakłócenie ujemne (np chłodzenie), regulator prawidłowo zareagował wzrostem sygnału sterującego s(t) (grzanie).
Rozdz. 24.6.8 Zakłócenie dodatnie na trójinercyjny z(t)=+0.5, Kp=25 Td=1 sek
Zakłócenie z(t)=+0.5 pojawi się w 30 sekundzie.

Rys. 24-36
Sygnał y(t) trochę buja. Zwłaszcza jako odpowiedź na x(t), bo odpowiedź na zakłócenie z(t) jest niezła. Na zakłócenie dodatnie (grzanie), regulator zareagował spadkiem sygnału sterującego s(t) (chłodzenie). Dzięki większemu wzmocnieniu Kp=25 uchyb e(t) w stanie ustalonym jest mniejszy niż dla Kp=10 na Rys.24-34
Rozdz. 24.6.9 Zakłócenie ujemne z(t)=-0.5, Kp=25 Td=1 sek
Zakłócenie z(t)=-0.5 pojawi się w 30 sekundzie.

Rys. 24-37
Bez komentarza

Rozdz. 24.7 Porównanie regulatora PD z regulatorem P
24.7.1 Wstęp
To tak jak FC Barcelona i LZS Progi Dolne. Zadamy jednocześnie ten sam skok jednostkowy x(t)=1 z zakłóceniem z(t)=+0.5 w 30 sekundzie. Domyślasz się który jest Barceloną? Zbadamy 2 przypadki z nastawą Kp=10 i Kp=100 dla obiektu dwuinercyjnego.

Rozdz. 24.7.2 Regulator PD Kp=10, D=5 sek i regulator P Kp=10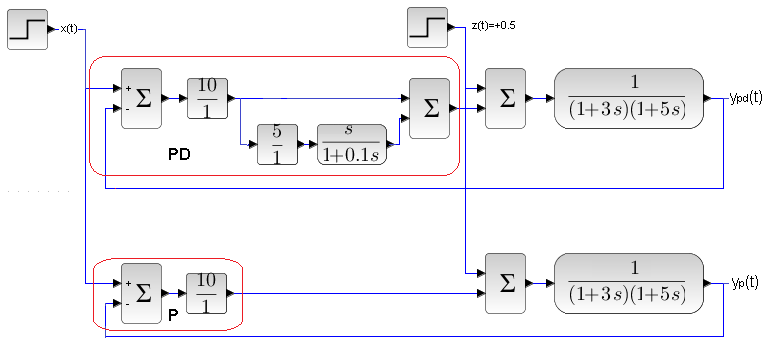

Rys. 24-38
Kp=10 Td=5 sek
Schemat 2 regulacji P i PD z tym samym obiektem dwuinercyjnym.

Rys. 24-39
PD jest bezkonkurencyjne dla wartości zadanej x(t) . Natomiast przy zakłóceniu z(t) to wynik jest dyskusyjny, ale raczej ze wskazaniem na PD. Ale zawsze można dać takie nastawy PD, żeby lepiej tłumiło zakłócenia, kosztem sterowania dla wartości zadanej x(t). Stany ustalone dla regulatorów PD i P są takie same. W regulatorze PD czas dojścia do stanu ustalonego jest znacznie krótszy (czytaj-lepszy) niż dla regulatora P.
Rozdz. 24.7.3 Regulator PD Kp=100, D=2 sek i regulator P Kp=100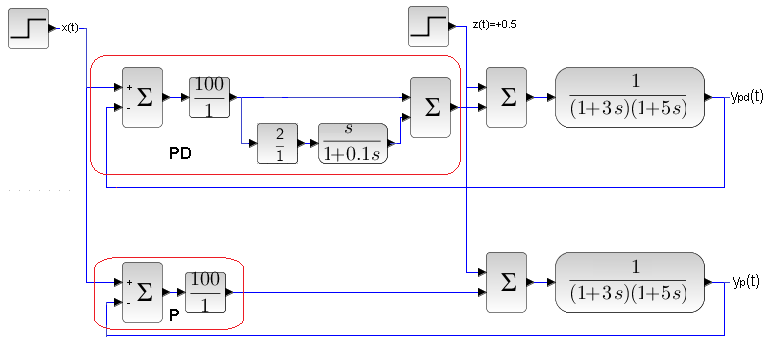

Rys. 24-40
Kp=100 Td=2 sek
Schemat 2 regulacji P i PD z tym samym obiektem dwuinercyjnym 

Rys. 24-41
Miażdżąca przewaga czerwonego  ypd(t) nad zielonym yp(t). Czyli regulacji PD nad P w odpowiedzi na  skok jednostkowy x(t).  Zwłaszcza, ze P daje straszne oscylacje. Jeżeli chodzi o tłumienie potężnego zakłócenia z(t)=+0.5 w 30 sekundzie, to dla PD i P jest tak dobre przy Kp=100, że prawie nie widać wpływu zakłócenia. Dlatego spójrzmy jeszcze raz na te przebiegi czasowe przy innym zakresie oscyloskopu 0.98…1.02.  Czyli użyjemy lupki.

Rys. 24-42
Tu wyraźnie widać, że także odpowiedź na zakłócenie jest wyraźnie lepsza dla regulatora PD.

Rozdz. 24.8 Regulator PD z osobnym różniczkowaniem sygnału wyjściowego y(t)
Rozdz. 24.8.1 Wstęp
Nazwa regulatora PD w tytule dość długawa. Niech będzie skrótowo PDy. Spójrzmy na poniższy rysunek.

Rys. 24-43
Do tej pory używaliśmy klasycznego regulatora PD takiego jak na Rys. 24-43a. Wzmacniany i różniczkowany jest uchyb e(t)=x(t)-y(t).
Tak jest w wielu podręcznikach i kursach automatyki. Okazuje się, że kiedy występują wolne procesy, np. w przemyśle chemicznym, częściej spotykamy się z regulatorami PDy z Rys. 24-43b. Tu różniczkowany jest tylko sygnał wyjściowy y(t), a nie uchyb e(t).
Na marginesie – używam skrótowo terminu „różniczkowany” zamiast „różniczkowany z inercją 0.1 sek”. Przypominam, że ta inercja służy do tłumienia zakłóceń szybko zmiennych.
Wróćmy do tematu.
Porównajmy 2 w/w struktury w 2 różnych stanach.
1- Stan ustalonym, gdy x(t),y(t) i z(t) są stałe.
Wtedy składowa różniczkująca jest zerowa. Tak jakby znikła gałąź różniczkująca regulatora. W tym stanie obydwa regulatory zachowują się jak regulatory P i dają sygnał wyjściowy y=Kz*x i uchyb e=Ke*x. Tu parametry Ke i Kz to wzmocnienia z Rys. 24-1. Czasy dojścia do stanu ustalonego dla każdej struktury będą oczywiście różne.
2- Gdy w stanie ustalonym przyszło zakłócenie z(t) .
Przykład – Temperatura w piecu doszła np. po 15 min do wartości ustalonej i ktoś po 25 min ktoś włączył ręcznie dodatkową grzałkę w piecu. Podkreślam nie regulator, tylko ktoś włączył dodatkową grzałkę. Typowe dodatnie zakłócenie z(t), na które regulator powinien zareagować obniżeniem mocy dostarczanej do pieca. Na Rys. 20-81 okaże się, że na zakłócenie obie struktury regulatora (z Rys. 24-43a i 24-43b) zareagują identycznie.
Spróbuję wyjaśnić to „po ludzku” i „z rachunkiem operatorowym”.
„Po ludzku”
Początek skoku x(t) wystąpił dawno. Wtedy możemy przyjąć, że sygnał x(t) jest stały. Czyli nie wpływa na gałąź różniczkującą regulatora.
Wtedy na gałąź różniczkującą wpływa tylko sygnał y(t) a właściwie -y(t) (ze znakiem minus!), a jeszcze ściślej -Kp*y(t).
Odpowiada to dokładnie Rys. 24-43b.
„Z rachunkiem operatorowym”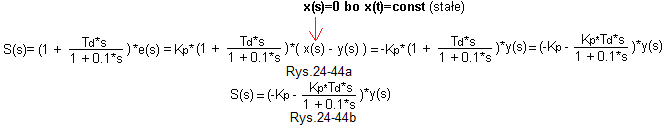


Rys. 24-44
Z obliczonej transformaty Laplace’a sygnału sterującego S(t) wynika, że dla stałego x(t) schematy Rys. 24-44a i Rys. 24-44b są równoważne.
Rozdz. 24.8.2 Regulacja PDy obiektu dwuinercyjnego z zakłóceniem z(t)=+0.5

Rys. 24-45
Realizacja schematu Rys. 24-43b dla Kp=10 i Td=5sek.
Jest to odpowiedź regulacji PDy, czyli regulacja PD z osobnym różniczkowaniem. Sygnał y(t) bardzo wolno dochodzi do stanu ustalonego y=0.91 i ledwo zdążył przed zakłóceniem. Na zakłócenie z(t)=+0.5 regulator zareagował prawidłowo obniżając sterowanie s(t). Porównaj przebiegi z Rys. 24-15 z klasyczną strukturę regulatora PD. Czyli z wersję z Rys. 24-43a. Do pojawienia się zakłócenia z(t) tj. do 30 sek. układ reaguje bardzo wolno! A to dlatego że został pozbawiony różniczkującego kopa od wartości zadanej x(t) w 3 sek. Działa tylko kop proporcjonalny s(t)=10 a nie s(t)=110 jak na Rys. 24-15. Potem działa słabnący sygnał od składowej proporcjonalnej (bo e(t) maleje). W dodatku składowa różniczkująca potężnie hamuje! Przestała hamować dopiero w 30 sek, gdy y(t) się ustalił.
Wnioski
Na Rys. 24-15 mieliśmy klasyczną wersję regulatora PD. Dla niej dobraliśmy takie nastawy Kp=10 i Td=5sek aby odpowiedź y(t) była optymalna.
Tu wchodzimy w inny temat. Co to znaczy optymalna? Jest dużo definicji na ten temat. Nam powinno wystarczyć intuicja. Odpowiedź y(t) jak najszybsza ze stosunkowo niedużą jedna oscylacją. Przyjęte metodą prób i błędów nastawy Kp i Td z grubsza zapewniły nam tak zdefiniowaną optymalność. Można przyjąć inną definicję. Np. najkrótszy przebieg y(t) bez oscylacji. Nie buja, za to czas regulacji będzie dłuższy.
Wróćmy do wniosków. Nastawy Kp=10 i Td=5 sek na Rys. 27-56 zapewniły najkrótszy czas regulacji przy skoku wartości zadanej x(t). Już wtedy mogło zdziwić, że odpowiedź na z(t) była nieoptymalna. Trochę długo. Z czego to wynika? Po prostu tor sygnału między z(t) a y(t) jest inny niż między x(t) a y(t). Czyli transmitancja wejściowa (między y(t) a x(t)) jest inna niż transmitancja zakłóceniowa (między y(t) a z(t)). A to oznacza, że nastawy które są optymalne dla transmitancji wejściowej nie są optymalne dla zakłóceniowej i vice versa.
I tu dochodzimy do najważniejszego wniosku.
1 – Gdy wartość zadana x(t) często się zmienia to stosujemy wersję regulatora PD czyli Rys. 27-77a
2 – Gdy wartość zadana x(t) rzadko się zmienia to stosujemy wersję regulatora PDy czyli Rys. 20-77b
Przykład 1 to samochodzik sterowany radiowo. Wejściem jest kierownica, którą masz na panelu sterującym z radiem a wyjściem kąt skrętu kół samochodu proporcjonalny do ruchu kierownicy.
Przykład 2 to lodówka. Często jest tak że ludzie latami nie zmieniają wartości zadanej temperatury x(t). Jest to przykład krańcowy, ale w przemyśle np. chemicznym wartość zadaną x(t) zmienia się rzadko, natomiast zakłócenia pojawiają się bez przerwy.
W przykładzie 2 nie jest więc ważne szybkie dojście y(t) do wartości zadanej, tylko szybka odpowiedź na zakłócenie.
Zapomniałem jeszcze o drugim ważnym plusie regulatora PDy. Przebiegi y(t) są łagodne. Także łagodniejszy jest sygnał sterujący s(t). Na obrazku może nie jest to takie ważne, ale gdy np. zawór na rurociągu w czasie przeregulowań ciągle „wali w dekiel” od otwarcia do zamknięcia, to długo nie pożyje! W następnym doświadczeniu nastawimy w regulatorze PDy nastawę Td ze względu na optymalność przebiegu od zakłócenia z(t).
Rozdz. 24.8.3 Regulacja PDy obiektu dwuinercyjnego z zakłóceniem z(t)=+0.5 z optymalną nastawą TD=1 sek

Rys. 24-46
Jest to realizacja schematu Rys. 24-43b dla Kp=10 i Td=1sek. Daliśmy mniejsze różniczkowanie Td=1 sek ze względu na optymalne tłumienie zakłócenia z(t) ( a nie skoku x(t) jak poprzednio).
Chyba szybsza odpowiedź na zakłócenie z(t) niż poprzednio. W dodatku poprawiła się odpowiedź na skok x(t) chociaż nie jest tak dobra jak na Rys. 27-57 dla regulatora klasycznego PD. No ale dla rzadko zmieniającej się wartości zadanej x(t) nie jest to najważniejsze.

Rozdz. 27.8.4 Porównanie klasycznej regulacji PD z regulacją PDy z osobnym różniczkowaniem
Porównajmy sterowanie PD optymalne dla x(t) (która jest nieoptymalna dla z(t)) ze sterowaniem PDy optymalnym dla z(t) (która jest nieoptymalna dla x(t)). Bełkotliwe, ale chyba wiemy o co autor chciał powiedzieć.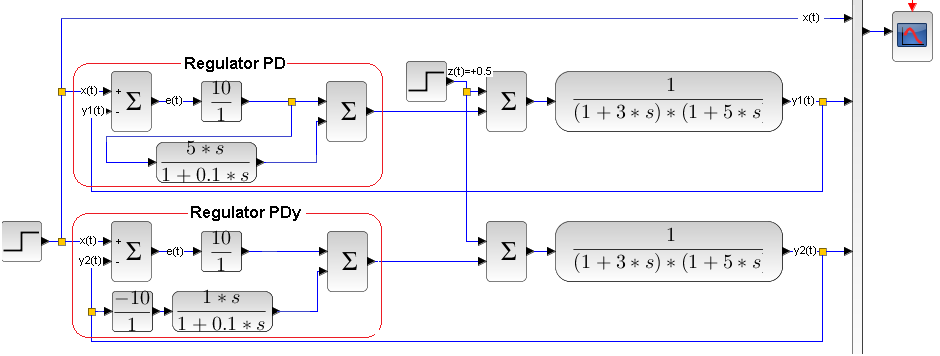

Rys. 24-47
Skok x(t) działa jednocześnie na układ regulacji klasycznej PD i układ regulacji z osobnym różniczkowaniem PDy. Są to układy optymalne ze względu na skok x(t) (schemat górny) i zakłócenie z(t) (schemat dolny).

Rys. 24-48
Obserwujemy tylko skok x(t), y1(t) i y2(t). Zakłócenie z(t)=+0.5 (którego nie ma na oscyloskopie!) pojawi się w 30 sekundzie.
Wnioski
1-W regulacji z osobnym różniczkowaniem PDy mniej przejmujemy się odpowiedzią na x(t) w których zmiany zachodzą stosunkowo rzadko. Dlatego możemy się skoncentrować na optymalizacji ze względu na zakłócenia z(t) które występują ciągle. Czyli podstawową rolą regulatora PDy jest optymalne tłumienie zakłóceń z(t), a nie optymalne (czytaj- ładne) dochodzenie do wartości ustalonej wyznaczonej przez x(t).
2- Dodatkową zaletą regulacji PDy są łagodniejsze przebiegi sterujące s(t).

Rozdz. 27.9 Wnioski z regulacji PD
1- Uchyb ustalony taki sam jak dla regulacji P
2- Znacznie lepsze własności dynamiczne niż regulacja P
3- Są regulatory PD z różniczkowaniem uchybu e(t)=x(t)-y(t) i PDy z różniczkowaniem tylko y(t).