How does CRC work?

Chapter 3 Logical Functions

Ch. 3.1 Introduction

I have already mentioned that CRC is treated as a kind of “remainder” of division. The “division” is the message being sent, the “divisor” is a certain constant known to the Transmitter and the Receiver, and the “rest” is the CRC. Wait, what’s most important, the result of division – “quotient“? This doesn’t interest us at all! Stop-more on this topic in Chapter. 4 CRC arithmetic. For now, I will only say that instead of division we will use something that is only similar to division. In fact, for “dividend” and “divisor” there is also a “remainder” which requires fewer bytes than “dividend“. And the most important. Instead of successive subtractions, we perform a very simple logical operation, xor-ing. In addition, there is no “nothing in memory” as in written decimal division. These operations are so simple and fast that they are ideal for calculating CRC. They are performed while sending the next bit and do not slow down the transmission. That’s why you need to be very good at xoring in later chapters.
But first you will learn the basic logic functions:
– NEGATION, i.e. denial
– AND, i.e. logical product
– OR, i.e. logical sum
and of course
– XOR means either

Chapter 3.2 Logical NEGATION function, also known as Denial

Fig. 3-1
Negator function in our way “NO”  ANIMATION
The output y is the negation of the input x, which we write as in the figure (y=x with a “caret”). Enter the animation and write the truth tablet.
If you don’t know what I mean, take a look at Fig. 3-5a in Chapter 3.6

Chapter 3.3 Logical OR Function, also known as Logical Sum
Fig. 3-2
OR function in our own words “OR”  ANIMATION
The function can be written as y=x1 or x2 or as a simple sum y=x1+x2
y=1 only if x1=1 or x2=1
Enter the animation, check the above sentence and write the truth tablet.

Ch. 3.4 Logical AND Function, also known as Logical Product

Fig. 3-3
AND function in our own words “AND” ANIMATION
The function can be written as y=x1 and x2 or as a simple product y=x1*x2
Y=1 only if x1=1 and x2=1 simultaneously
Enter the animation, check the above sentence and write the truth tablet.

Chapter 3.5 XOR Logic Function

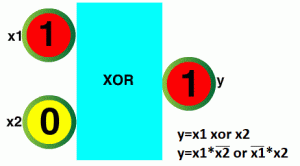
Fig. 3-4
XOR function in our own words “EITHER” ANIMATION
Y=1 only if x1=1 or x2=1
Enter the animation, check the above sentence and write the truth tablet.
By the way. Some people do not distinguish the conjunction “OR” from “EITHER”.
Our law allows marriage “to Jola either to Mariola” but not “to Jola or to Mariola”. The latter would allow bigamy!

Chapter 3.6 Logical Functions in the form of truth tables (Karnaugh tables)

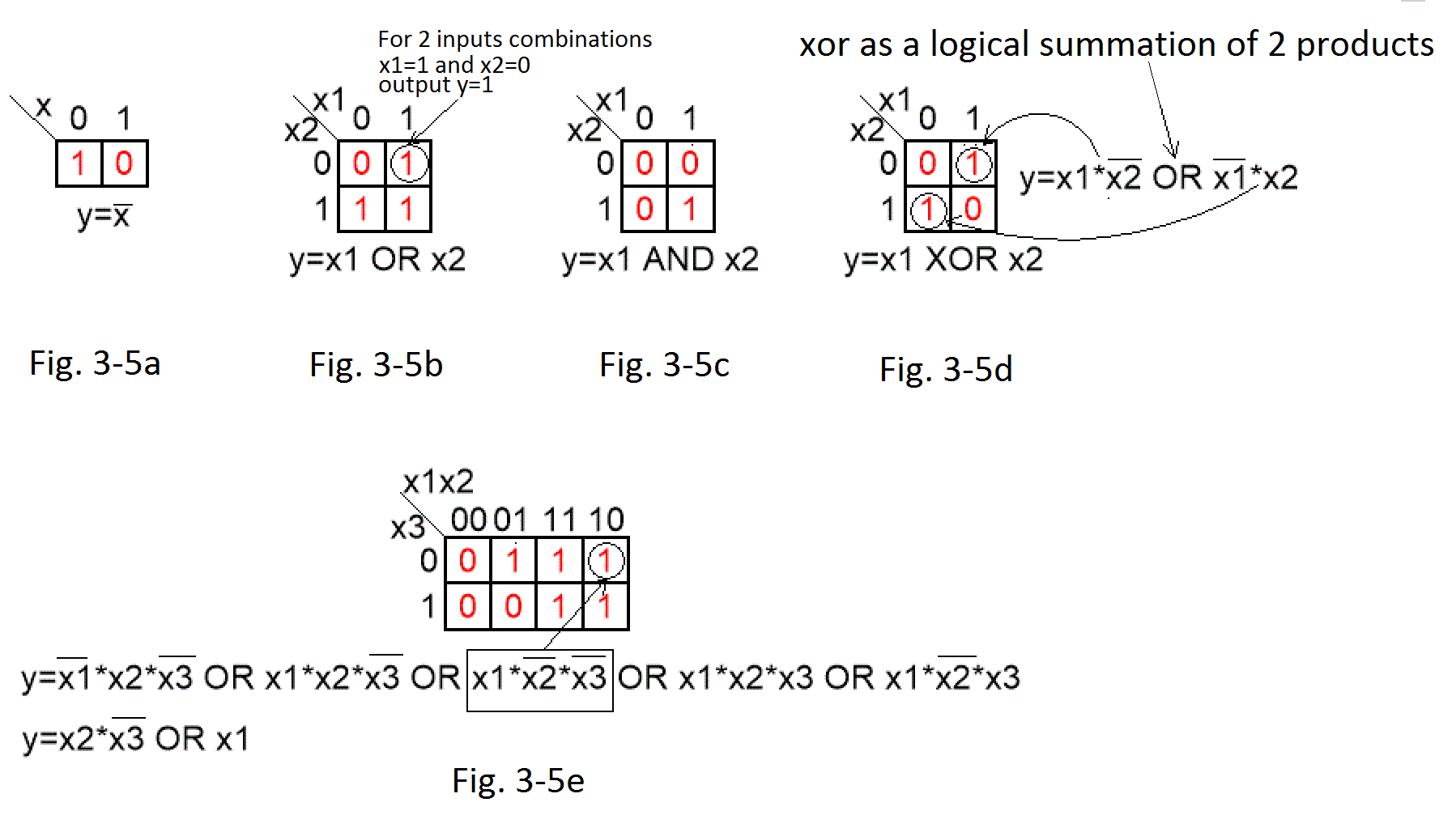
Fig. 3-5
Truth tables
It is very convenient to present a given logical function in the form of the so-called truth tables. Especially when we are examining a device and we do not yet know its logical function. Fig. 3-5a…3-5d are the results of testing the logic circuits from Chap. 3.2…3.5. Each cell of the truth table corresponds to one tested input combination. For example, in Fig. 3-5b regarding the OR function, circled 1 means that for the combination of inputs x1=1 and x2=0, output y=1. This function has 2 inputs x1 and x2 for which there are 4 different combinations of inputs x1 and x2. Therefore, its truth table is a 2×2 square. This note applies to all tested systems with 2 inputs. The OR symbol can be replaced with “+”, and the AND symbol with the multiplication symbol “*”. They are probably even more popular.
Fig. 3-5a
Negator
For input x=0 output y=1 and for input x=1 output y=0. This is the result of testing the negator in Figure 3-1.
Fig. 3-5b
OR
Fig. 3-5c
AND
Fig. 3-5d
i.e. the XOR function well illustrates the fact that each 1 is a separate logical product of x1 and x2. Here, some x1*x2 in the product are “covered”, i.e. negated.
Now a question may arise. While this is obvious for the AND and XOR functions, the OR function should consist of 3 appropriately overlapped products! And here it is just simple y=x1+x2! It turns out that any logical function given in the form of a table can be simplified! In the 1950s, a man named Karnaugh showed how to do this in one limited case. Namely, for functions with a maximum of 5 inputs x1, x2, x3, x4, x5, he used the so-called gluing. And this is nothing more than a logical law that we use every day. I will say no more about its details than the following.
You can say “Tomorrow the sun will shine and it will rain, or tomorrow the sun will shine and it won’t rain.” I hope you see the sum of 2 logical products here! The same thing can be said much more simply, “The sun will shine tomorrow.” It’s absolutely the same content! That’s why future parrots (advocates) in law schools learn mathematical logic. Then, when defending the client in court, they express themselves briefly and concisely.
Fig. 3-5e
This is an example of a function with 3 inputs x1 x2 x3. Each cell is a different combination of these inputs corresponding to a different product. Try to work out the product with a circle yourself, especially the carets-negations with the appropriate zeros x2 x3, as well as combinations for the remaining 4 cells of the table with 1. For this function with 3 inputs, we have a table of dimensions 2×4. Similarly, for 4-input functions there is a 4×4 table and for 5-input functions there is a 4×8 table. Returning to Fig. 3-5e, the same function can be presented in a “raw” form, so to speak. In other words, canonical, i.e. in the form of 5 products with 3 components each. Thanks to Mr. Karnaugh, using the so-called gluing, it can also be presented as just two products. Moreover, they are shorter, because the first one has only 2 components and the second one 1. Therefore, the computer program performing this function, will be simpler, cheaper and more reliable.
You can find more about the Karnaugh method online.