How does CRC work?

Chapter 4 CRC Arithmetic 
Ch. 4.1 Introduction

We will start with a topic that you already know from primary school, which is written division. Then you will see that calculating CRC is similar, only much simpler. You don’t have to wonder how many times “something” fits into “something”. There is nothing “in memory” either. You just xor and move!

Chapter 4.2 Example of decimal division

Fig. 4-1
Example of written decimal division  
Remind yourself of sharing by clicking  ANIMATION

Chapter 4.3 Xor-ing exercises
Before we move on to calculating CRC, you need to be good at xoring line expressions.

Fig. 4-2
Below the dash of each xor is a row whose element is the xor of the elements in the column above it. Check this for Fig. 4-2a and 4-2b.
With a larger number of rows, as in Fig. 4-2c, the result is 0 when there are an even number of ones in the column and 1 when there are an odd number.

Chapter 4.4 Example of CRC calculation
This is one of the most important points in this course

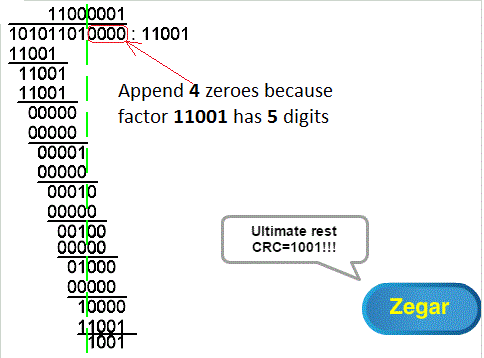
Fig. 4-3
Example of calculating CRC as the “remainder” of “division” ANIMATION
This action only resembles division, which is why I used quotation marks.
We “divide” the “dividend” 10101101 by the “divisor” 11001. The “quotient” 11000001 obtained above the line does not interest us. Only the remainder of the “division” 1001 is important.
Compare with written division from Chapter 4.2 and try to determine the algorithm yourself.
It should be as follows.
1. Add 4 zeros because the dividend has 5 digits
2. Write the first 1 in 5 positions above the top line because the divisor 11001 has 5 digits
3. Calculate the first “remainder” as in regular decimal division. So from 10101 we “subtract” 1×11001=11001. We replace “subtraction” with xor-ing. The first remainder is 1100.
4. Add 1 to the “quotient” above the upper line because the first remainder was non-zero. If it was zero, you would add 0. Other words-do not do anything.
Calculate the second remainder. It is 0000.
…
e.t.c
The calculation ends when the next “remainder” is exactly under the added 4 “zeros”. The final “remainder” will be 1001.
Now try to calculate the rest yourself on a piece of paper. That is, calculate the remainder of the “division” 10101101:11001.
The result obtained is CRC=1001 from the sent message when the “divisor” is 11001.

Chapter 4.5 Modification of CRC calculation
What if, instead of 0000, we added 1001 as the remainder of the division from the previous example? So what CRC will we get now?
I think the answer I hear is CRC=0000. Bravo, you won the TV! Well, let’s check.

Fig. 4-4
What is the “remainder” when instead of “0000” we add “1001” as the “remainder” from the previous example?  ANIMATION
We “divide” the “dividend” 10101101 by the “divisor” 11001. Note that until the fourth remainder, the “division” procedure is identical as before. This is obvious because the added 1001 does not affect the actions yet. As we expected, ultimately CRC=0000.
In the next chapter, you will find that this algorithm is also used in data transmission. For some, it’s even more elegant!