Fourier Transform

Chapterł 1 Introduction.

We already know that almost every periodic function f(t) can be decomposed into cosine and sine with different amplitudes An and Bn and with pulsations nω0. What about “normal” functions f(t), i.e. aperiodic functions? It is similar, only their decomposition into harmonics is more difficult to imagine. Their amplitudes An and Bn are infinitesimally small. Successive harmonics are located infinitely close to each other. Otherwise, their subsequent pulsations nω0 and (n+1)ω0 are “almost” the same. And the “first harmonic” for ω0=0 is an infinitesimal constant component! For now, the above text may not be entirely clear. You definitely will after reading the entire article. But I think you’ll notice the analogy between the Series and the Fourier Transform.

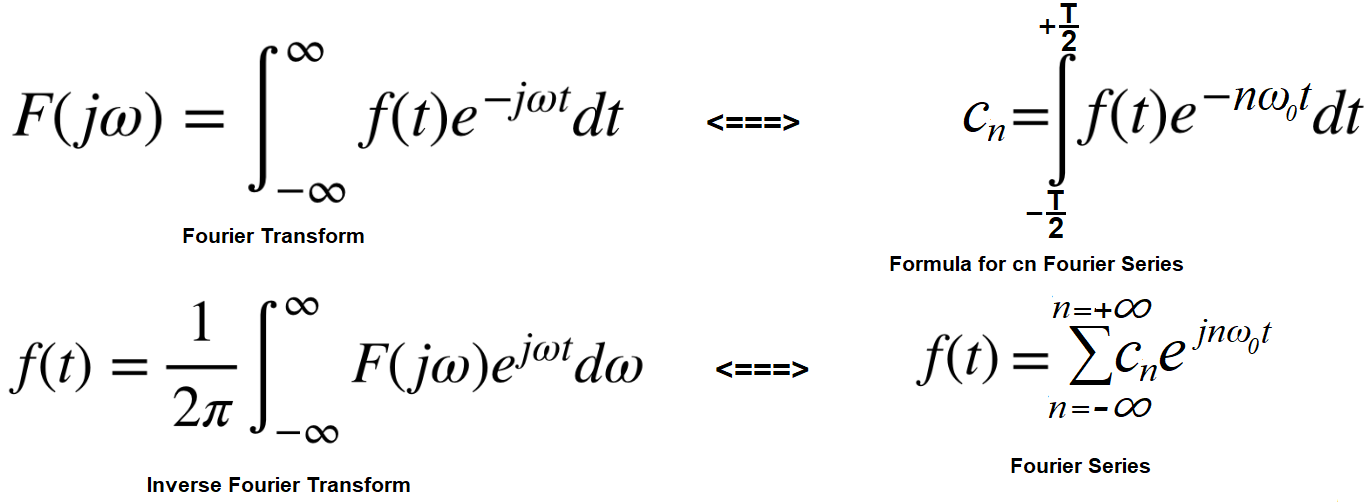
Fig. 1-1
Analogies
1. The Fourier transform F(jω) is equivalent to the formula for the nth complex amplitude cn of the Fourier Series. Both, i.e. F(jω) and cn were created based on the time function f(t).
2. The Inverse Fourier Transform is equivalent to the Fourier Series formula. Both of them again build the function f(t) based on harmonics.