Transformata Fouriera
Rozdział 1 Wstęp.
Wiemy już, że prawie każdą funkcję okresową f(t) można rozłożyć na cosinusoidy i snusoidy o różnych amplitudach An i Bn i z pulsacjami nω0. A co z funkcjami “normalnymi” f(t), czytaj nieokresowymi? Jest podobnie, tylko ich rozkład na harmoniczne jest trudniejszy do wyobrażenia. Ich amplitudy An i Bn są nieskończenie małe. Kolejne harmoniczne są położone nieskończenie blisko siebie. Inaczej ich kolejne pulsacje nω0 i (n+1)ω0 są “prawie” takie same. A “pierwsza harmoniczna” dla ω0=0 jest nieskończenie małą składową stałą! Na razie powyższy tekst może nie być do końca jasny. Na pewno będzie po przeczytaniu całego artykułu.
Ale chyba zauważysz analogię między Szeregami a Transformatą Fouriera.
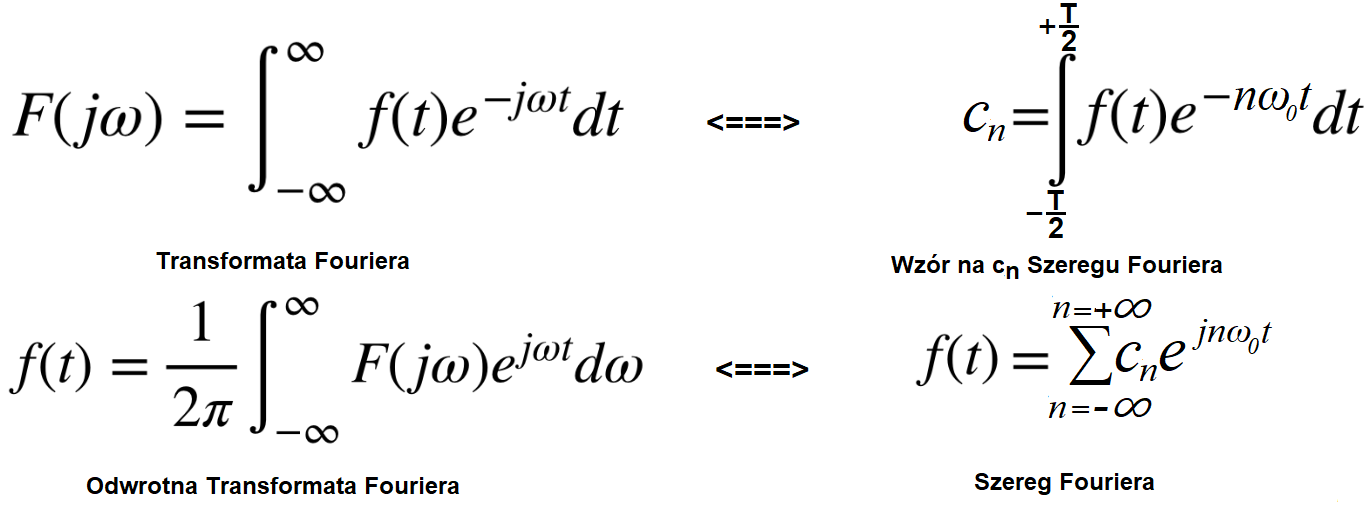
Rys. 1-1
Analogie
1. Transformata Fouriera F(jω) jest odpowiednikiem wzoru na n-tą amplitudę zespoloną cn Szeregu Fouriera.
Obydwie, tj. F(jω) i cn powstały na podstawie funkcji czasu f(t)
2. Odwrotna Transformata Fouriera jest odpowiednikiem wzoru na Szereg Fouriera.
Obydwie ponownie budują funkcję f(t) na podstawie harmonicznych.
