Jak działa CRC?
Rozdział 5 Obliczanie CRC na rejestrach
Rozdz. 5.1 Wstęp
Umiesz już ręcznie obliczać CRC i jest to dużo prostsze od zwykłego dzielenia dziesiętnego. Algorytm to tylko przesunięcia i ewentualnie xor-owania. Można je więc łatwo realizować na rejestrach przesuwnych wspomaganych prostą logiką opartą na xor-owaniu.
Rozdz. 5.2 Układ Obliczania CRC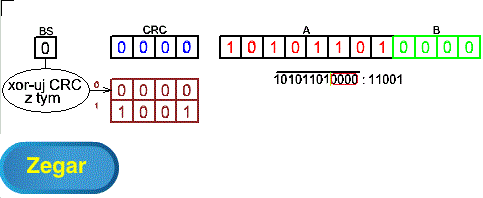
Rys. 5-1
Układ Obliczania CRC ANIMACJA
Układ składa się z rejestrów przesuwnych “w lewo” BS CRC A B oraz tablicy 2×4 służącej do modyfikacji CRC po przesunięciu. Jest to elektroniczna realizacja obliczania “reszty” z “dzielenia” 10101101:11001 którego arytmetyka opisana została w Rozdz. 4.4. Przypominam, że rejestr A zawiera “dzielną” czyli przesyłaną wiadomość. Może on być dowolnej długości. Wejdź w animację i samemu rozpracuj działanie. Dla ułatwienia pokazany jest każdy stan ręcznego obliczania CRC. Ale prawdę powiedziawszy można na to nie zwracać uwagi.
Każdy impuls zegarowy przesuwa zawartość rejestrów BS CRC A B w lewo.
Dzielnik 11001, a ściślej tylko jego 4 młodsze bity 1001 umieszczone są w 2-elementowej pamięci stałej ROM pod adresem 1.
Pod adresem 0 jest 0000.
Po każdym przesunięciu wykonywana jest operacja xor:
Gdy BS=1 to CRC=CRC xor 1001
Gdy BS=0 to CRC=CRC xor 0000 czyli CRC jest tylko przesunięte
CRC jest ostatecznie obliczone gdy rejestry A B są puste.
Eksperymentuj dopóki wszystko będzie dla Ciebie jasne.
Uwaga:
Animacja jest tu bardzo dokładna tzn. etapy przesunięcia i xor-owania są rozdzielone. W następnych przykładach kursu stanowią już
tylko jeden wspólny etap, co jest jednak pewnym utrudnieniem. Dlatego apeluję o dokładne zrozumienie zasady działania po to, by później nie wchodzić w zrozumiałe już szczegóły.
Rozdz. 5.3 Rejestr przesuwny z liniowym sprzężeniem zwrotnym
Inaczej LFSR Linear-Feedback Shift Register
Jest to inna realizacja układu z Rozdz. 5.2
Skąd ta nazwa? Rejestr przesuwny bo przesuwa. Sprzężenie zwrotne bo sygnał w rejestrze zawraca. A liniowe?
To niech już będzie jak w zagadce.
Co to jest? Wisi na ścianie, zielony i śpiewa.
Przecież to oczywiste, że śledź!
Wisi bo go powiesili
Zielony bo pomalowali
A śpiewa żeby było trudniej zgadnąć.
A tak na serio. Jest to rejestr przesuwny, w którym stan D3 D2 D1 D0 jest funkcją liniową poprzedniego stanu D3 D2 D1 D0.
A funkcją liniową jest właśnie xor. A dlaczego xor jest funkcją liniową? Tu dajmy sobie spokój.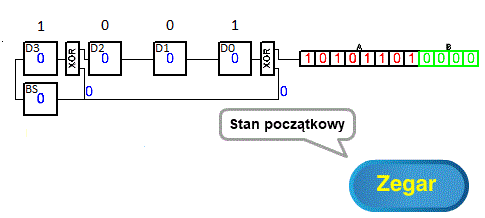
Rys. 5-2
Układ Obliczania CRC jako LFSR ANIMACJA
Jak zbudować LFSR?
1. Napisz wszystkie bity “dzielnika” oprócz najstarszego. Tu 1001 bo “dzielnikiem” jest 11001
2. Pod każdą cyfrą 1001 umieść przerzutnik typu D-element pamiętający (umieściłeś D3 D2 D1 D0)
3. Umieść bramkę XOR za każdym przerzutnikiem nad którym jest 1
4. Połącz wszystko tak jak na Rys. 5-2
W ten sposób zaprojektowałeś rejestr LFSR. Wejdź w animację i po kolejnych kliknięciach-impulsach zegarowych rejestr LFSR obliczy “resztę z dzielenia” 10101101 tj. liczby znajdującej się w rejestrze A. Czyli LFSR oblicza CRC z wiadomości znajdującej się w rejestrze A o dowolnej długości-przeważnie wielokrotność bajtu.
Analogicznie budujesz rejestry dla innych “dzielników”.
Początek animacji jest łatwy, gdyż na “dolnych” wejściach xor-ów jest stan 0. Dane są tylko przesuwane. Potem, tę przyjemną analizę zakłócają stany 1, które mogą pojawić się na wejściach xor-ów.
Zauważ, że komentarze w chmurkach które ułatwiają analizę działania, są w czasie przyszłym:
– Tylko przesunę bo D3=0
– Przesunę i xor bo D3=1
Spróbuj przewidywać stan następny D3 D2 D1 D0 po kliknięciu zegara.
Rozdz. 5.4 Przykład transmisji Nadajnik-Odbiornik
Jest realizacja algorytmu z Rozdz. 4.4 gdy do dzielnej dopisujemy 0000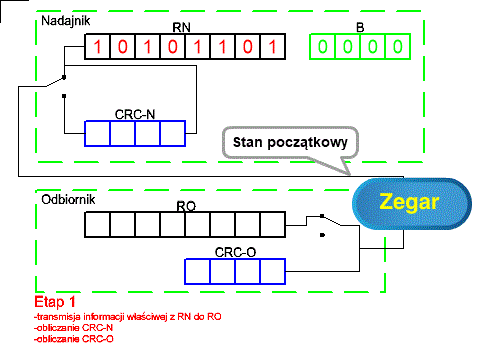
Rys. 5-3
Transmisja Nadajnik-Odbiornik ANIMACJA
Naszym cele jest przeniesienie informacji z RN w nadajniku do RO w odbiorniku. W dodatku odbiornik musi wiedzieć, że najprawdopodobniej w czasie transmisji nie było błędów. W tym celu w nadajniku i odbiorniku są rejestry CRC-N i CRC-O, które niezależnie od siebie obliczają CRC. Może on być zrealizowany jako CRC, BS i ROM z Rys. 5-1 lub LFSR z Rys. 5-2. Przy okazji. W chmurkach animacji pojawiają się komunikaty typu RN–>CRC-N lub RN–>CRC-0. Nie jest to jednak zwykłe przeniesienie, ale przeniesienie plus obliczenie nowego CRC tak jak na Rys. 5-1 lub Rys. 5-2!
Etap 1 transmisja RN–>RO + obliczanie CRC w CRC-N i CRC-O.
Etap 2 dokończenie obliczania CRC w CRC-N i CRC-O (“wpychanie” 0000 do tych rejestrów).
Etap 3 transmisja CRC-N –> CRC-O i ich porównanie. Gdy takie same to transmisja prawidłowa.
Uwaga
W rzeczywistej transmisji wysyłana wiadomość, czyli zawartość RN może mieć tysiące bajtów!
Rozdz. 5.5 Przykład transmisji Nadajnik-Odbiornik “z dopisaną resztą”
Jest realizacja algorytmu z Rozdz. 4.5 gdy do dzielnej dopisujemy 1001 czyli resztę końcową CRC.
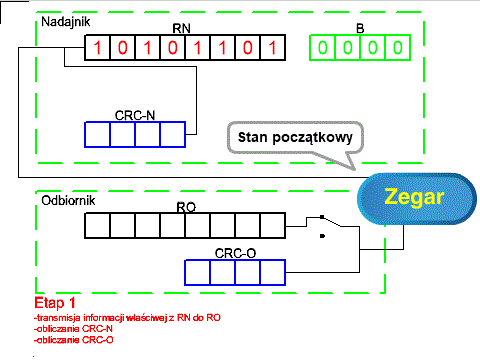
Rys. 5-4
Transmisja Nadajnik-Odbiornik “z dopisaną resztą” ANIMACJA
Dziwne. Rejestr B=0000 a powinien być B=1001 bo taka jest “dopisana reszta! Mało tego. Rysunek jest taki sam jak Rys. 5-3! Sprawa jest oczywista. Etap 1 jest dokładnie taki sam jak w poprzednim rozdziale. W stanie początkowym B=0000 bo Nadajnik nie wie jeszcze jakie jest CRC. Dopóki te zera nie “dojdą” do CRC-N i CRC-0 to nie mają one żadnego wpływu na CRC-N i CRC-0. Na końcu etapu 1 odbiornik zapamięta stan CRC-O w rejestrze copy po to by na końcu etapu 2 “przypomnieć” go sobie. Rejestr copy zobaczysz w animacji. Dalej algorytm pójdzie jak w Rozdz. 4.5, tak jakby od samego początku było B=1001. Stanem końcowym będzie CRC-O=0000, czyli transmisja była bezbłędna.
Rozdz. 5.6 Software czyli program obliczający CRC
Program napisany jest w zrozumiałym dla każdego pseudojęzyku.
Czytelnik-programista bez problemu zamieni go na swój ulubiony język np. C lub assembler. Uwaga ta dotyczy też następnych rozdziałów.
Rejestry BS CRC A B z Rys. 5-1 tworzą wspólny rejestr przesuwny BS_CRC_A_B. Instrukcja Wpisz A do CRC w lewo naszego pseudojęzyka, wpisuje nie tylko początkowy bit z A do CRC, ale też przesuwa cały rejestr BS_CRC_A_B o 1 bit w lewo. Po każdym przesunięciu badany jest jednobitowy rejestr BS i CRC jest xor-owane z wierszem tablicy wskazanym przez BS. Po wprowadzeniu ostatniego bitu z A do CRC rejestr A jest pusty i oznacza to zakończenie programu. Wtedy CRC zawiera obliczoną resztę.
Opis tablicy:
Tablica(0)=0000
Tablica(1)=1001=generator czyli wszystkie bity “dzielnika” oprócz najstarszego.
W naszym przypadku, dotyczącym także rozdz. 4.4, “dzielnik“=1 1001 czyli generator=1001.
Program w pseudojęzyku
Wpisz wiadomość do A
Wpisz zera do B
Dopóki CRC niepuste
{ Wpisz A do CRC w lewo
CRC=CRC xor tablica(BS) }
Dla BS=0 mamy CRC= CRC xor tablica(BS=0) = CRC xor 0000 = CRC czyli jest tylko przesunięcie.
Dlatego program może być przedstawiony również w postaci równoważnej:
Wpisz wiadomość do A
Wpisz zera do B
Dopóki CRC niepuste
{ Wpisz A do CRC
jeżeli BS=1 to CRC=CRC xor generator }
Ta wersja jest chyba na
