Szeregi Fouriera Klasycznie

Rozdział 2  Trygonometryczny Szereg Fouriera
Rozdział 2.1 Wstęp
Rozłóżmy na Szereg Fouriera funkcję f(t) o okresie T=2π/sek odpowiadającym pulsacji ω=1/sek.
Na razie przyjmij te wzory na słowo honoru.

Rys. 2-1
Rozkład funkcji f(t) na Szeregu Fouriera gdzie:
a0-składowa stała
1ω– pulsacja  pierwszej harmonicznej równa pulsacji funkcji f(t) tu 1ω=1/sek.
2ω, 3ω…- pulsacje kolejnych harmonicznych jako wielokrotności pierwszej
a1, a2 …- amplitudy kolejnych harmonicznych cosinusoid
b1, b2 …- amplitudy kolejnych harmonicznych sinusoid
Parametry a0, a1, a2 …b1, b2 …an,bn liczone powyższymi całkami, to konkretne wartości
Np. dla w.w fali prostokątnej
a0=a1=a2=…=0
b2=b4=b6=…=0
b1=4/π=1.273, b3=4/3π, b5=4/5π…   itd
Dla fali prostokątnej na rysunku występują tylko nieparzyste współczynniki bn. Parzyste bn i wszystkie an są zerowe. Czyli występują tylko sinusy. To się zgadza z intuicją ponieważ sinus i fala prostokątna jest funkcją nieparzystą. Gdyby wykres był przesunięty o π2 w lewo, to fala prostokątna byłaby funkcją parzystą i byłyby tylko cosinusy.
Najczęściej  Szereg Fouriera  jest nieskończony ale nie zawsze tak jest.
Przykład suma sinusoid:
f(t)=1.25sin(1t)+0.25sin(2t)
Ten szereg ma tylko 2 współczynniki  b1=1.25 i b2=0.25. Pozostałe są zerowe.
Pulsacja ω może mieć dowolną wartość. Często są to ω=1/sek lub ω=2π/sek  i wtedy Szeregi Fouriera mają postać:

Rys. 2-2
Rys. 2-2a ω=1/sek      przebieg wolniejszy odpowiadający okresowi T=2π sek ≅6.28 sek
Rys. 2-2b ω=2π/sek  przebieg szybszy –> T=1 sek.

Rozdział 2.2 Analiza Szeregów Fouriera-Pierwsze podejście
Ciekawe co miał w głowie Jean Baptiste Joseph Fourier w 1806 roku? Jak na to wpadł, że dowolna funkcja f(t) jest sumą sinusoid i cosinusoid?  Nie wiem, ale mogło być tak.
Cała sztuka polega na znalezieniu odpowiednich współczynników ω,a0,a1,a2…b1,b2…równania f(t)=… z Rys 2-1. Podejdźmy do sprawy z drugiej strony. Tzn. znamy funkcję f(t) i jest nią suma 3 sinusoid. Żeby było łatwiej, to cosinusoidy nie występują! Do jej rysowania a później także do obliczeń wykorzystamy niesamowity program z internetu WolframAlpha. Nie musisz go znać. Wywołaj tylko i wpisz w odpowiednie pola to co każe poniższy obrazek. W ten sposób zostanie narysowana funkcja f(t) w zakresie t=-2π…+2π. Przekonasz się jak prosty i użyteczny jest ten program. O samym programie WolframAlfa napisałem więcej w kursie Szeregi Fouriera Wirująco w rozdz. 11.2. Kliknij więc https://www.wolframalpha.com i zrób co każe obrazek. Zresztą, możesz być mniej ambitny i poprzestać tylko na oglądaniu gotowych wykresów.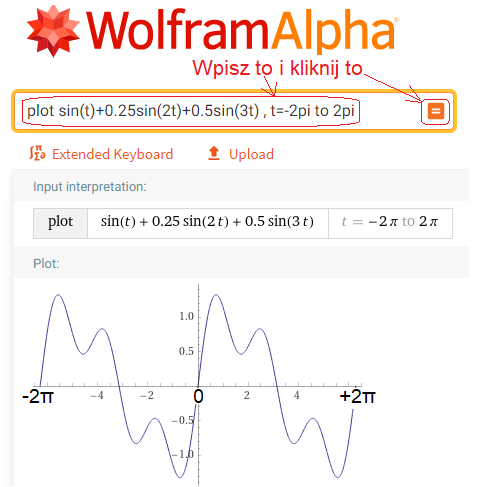

Rys. 2-3
Funkcja f(t) została obliczona i narysowana poleceniem “plot” czyli “wykreśl”.
Dziedziną funkcji jest t=- ∞…+ ∞ chociaż wykres przedstawia tylko t=-2π…+2π
Jest to suma sinusoid o pulsacjach i amplitudach :
pierwsza harmoniczna–> ω=1/sek (czyli T=2π sek) o amplitudzie b1=1
druga harmoniczna–>2ω=2/sek o amplitudzie b2=0.25
trzecia harmoniczna–>3ω=3/sek o amplitudzie b3=0.5
Pierwsza harmoniczna odpowiada pulsacji ω=1/sek naszej badanej funkcji f(t) czyli okresowi T=2π sek.
Następne pulsacje to wielokrotności pierwszej harmonicznej.
Pozostałe parametry tzn. b4,b5…a0, a1,a2..są zerowe. Jest to przykład Szeregu Fouriera o skończonej liczbie elementów n=3 o którym wspomniałem w Rozdziale 1.
A teraz wyobraź sobie, że znasz tylko wykres funkcji f(t) ale nie znasz wzoru. Wiesz tylko tyle, że są 3 składowe sinusoidalne o nieznanych pulsacjach ω1, ω2 i ω3 i nieznanych amplitudach b1, b2 i b3.
Co do składowej stałej a0 to ewidentnie jest a0=0. Pola “nad” i “pod funkcją f(t)” są takie same!
Okres T pierwszej harmonicznej ω1 powinien być taki sam jak funkcji f(t), czyli T=2π sek! Przecież pierwsza harmoniczna jest pierwszym przybliżeniem tej funkcji. Czyli ω1=ω=1/sek.
Jakie jest ω2 i ω3? Powinny być wielokrotnościami ω=1/sek czyli ω2=2/sek i ω3=3/sek. W przeciwnym razie harmoniczne nie spotkałyby się w t=-2π, t=0, t=+2π … A muszą się spotkać aby w tych punktach było f(t)=0.  Dzięki temu f(t) powtarza się co T=2π sek.
Przejdźmy teraz do pozostałych parametrów tj do amplitud sinusoid b1, b2 i b3? Może by tak badać różne ich kombinacje i wybrać takie b1, b2 i b3 przy których suma sinusoid jest najbardziej zbliżona do funkcji f(t)?  Po wielu, może nawet po 100 próbach rysowania wykresu otrzymamy coś najbardziej zbliżonego do f(t) z Rys. 2-3. Kombinacją  okaże się np. b1=0.98, b2=0.2 i b3=0.48. Prawie sukces. Są to wartości zbliżone wzoru  Przypominam, że znamy tylko wykres f(t) ale bez wzoru! Metoda prymitywna, pracochłonna i przypominająca zgadywankę.  Jest  jednak często stosowana gdy wema twórcza zawodzi. Zawsze to lepsze niż wywieszenie białej flagi.

Rozdział 2.3 Analiza Szeregów Fouriera-Drugie podejście z wyłuskiwaniem harmonicznych
Pan Fourier zdawał sobie sprawę, że “zgaduj-zgadula” z poprzedniego rozdziału jest tylko wstępem do rozwiązania problemu. Jakby tu sprytnie wyłuskać poszczególne  3 nieznane harmoniczne? A właściwie tylko 3 amplitudy b1, b2 i b3 bo pulsacje 1ω,2ω i 3ω już znamy.  A może tak?

Rys. 2-4
Jak wyłuskać  składową stałą, pierwszą, drugą i trzecią harmoniczną?
Rys. 2-4a
Napoleon- który znał matematykę zagadnął Fouriera*.
Drogi Jean Baptiste- pomyślałem sobie jakąś funkcję f(t) składającą się z 3 sinusoid.
Jaka to funkcja? Dla ułatwienia powiem, że jej wykres to Rys. 2-3  i jej kolejne pulsacje to 1ω=1/sek, 2ω=2/sek i 3ω=3/sek. Podkreślam. Nie znasz wzoru funkcji z Rys. 2-3, znasz tylko jej wartości w zakresie -2π…+2π czyli jej wykres.
Rys. 2-4b
Fourier zapisał sobie tą funkcję z 3 nieznanymi mu jeszcze współczynnikami b1, b2 i b3 zaczął główkować. Najpierw znajdźmy b1.
Rys. 2-4c
Szukam b1, dlatego pomnóżmy obie strony równania przez sin(1t)! Skąd mu się to wzięło. Chyba sam nie wiedział. Pewnie intuicja. Wybiegając w przyszłość, to gdybyś szukał np.  b2 to pomnnóż przez sin(2t).
Rys. 2-4d
A może by tak scałkować obie strony w okresie  tu T=2π. Skąd taki pomysł Fouriera? Też chyba intuicja.
Rys. 2-4e
Całka rozbita na sumy.
Rys. 2-4f
Wyłączenie b1, b2 i b3 przed całkę.
Rys. 2-4g
A teraz najważniejsze. Dwie całki się wyzerowały a pierwsza ma wartość π!
Wyjaśnienie w rozdziale 2.6.
Rys. 2-4h
Wzór na b1 dla pulsacji ω=1 ściślej ω=1/sek. Czyli dla T=2π/ω=2π ściślej T=2πsek
Rys. 2-4i
Wzór na b1 dla pulsacji dowolnej ω. Czyli dla T=2π/ω.
Dla ω=1 wzór przekształca się w Rys. 2-4h.
Rys. 2-4j
Ostateczny wzór na a0, b1,b2 i b3 dla funkcji f(t) z wykresu na Rys. 2-3.
-a0  jest to składowa stała f(t) czyli średnia arytmetyczna. Tak się oblicza średnią funkcji o okresie T.
-b1 opisano na Rys. 2-4a…2-4i
-b2 Jeśli na Rys. 2-4c zamiast sin(1t) wstawimy zamiast sin(2t) to otrzymamy b2
-b3 Jeśli na Rys. 2-4c zamiast sin(1t) wstawimy zamiast sin(3t) to otrzymamy b3
*Uwaga
Nie wiem czy akurat dokładnie tak było, ale faktem jest że panowie znali się. Sam Napoleon był nawet  dobrym matematykiem i podobno jest nawet autorem twierdzenia o tzw. “punktach Napoleona”. Niektórzy, chyba nie lubiący wodza, to kwestionują.

Rozdział 2.4  Sprawdzenie wzoru
Rozdział 2.4.1 Wstęp
Czy po zastosowaniu wzoru Rys. 2-4j dla funkcji f(t) z Rys. 2-4a  otrzymamy?
a0=0
b1=1
b2=0.25
b3=0.5
Trochę jak w zagadce “Po wodzie pływa, kaczka się nazywa”. Przecież  widać to na Rys. 2-4a! Tak, ale te współczynniki służą tylko do obliczenia wartości f(t)! Po to tylko, żeby ze wzorów z całkowaniem Rys. 2-4j otrzymać, mam nadzieję prawidłowe współczynniki. Innymi słowy, tak jakbyśmy mieli do dyspozycji tylko wykresy f(t).

Rozdział 2.4.2  Składowa stała-a0
Wprowadź wzór na a0 z Rys. 2-4j gdy T=2π do wolframAlpha.
Wywołaj https://www.wolframalpha.com i rób co każe obrazek.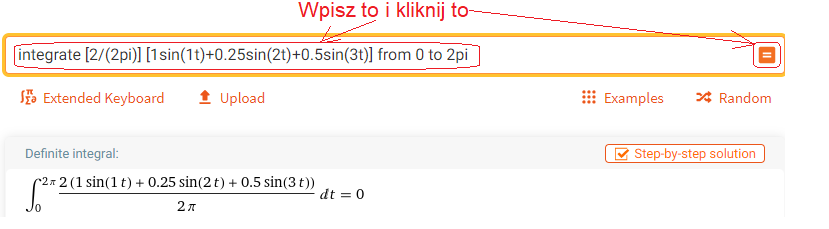

Rys. 2-5
Obliczanie a0– składowej stałej
Tak, jak się spodziewaliśmy a0=0. Widać to zresztą na Rys. 2-3.  “Pola nad i pod” są równe.

Rozdział 2.4.3  Amplituda pierwszej harmonicznej-b1
Wywołaj https://www.wolframalpha.com i rób co każe obrazek.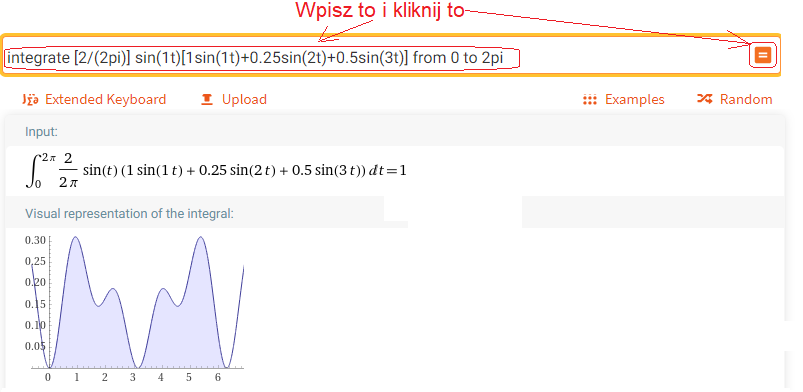

Rys. 2-6
Obliczanie b1– amplitudy pierwszej harmonicznej
Zgadza się, b1=1, dodatkowo całka została przedstawiona jako pole

Rozdział 2.4.4  Amplituda drugiej harmonicznej-b2
Wywołaj https://www.wolframalpha.com i rób co każe obrazek.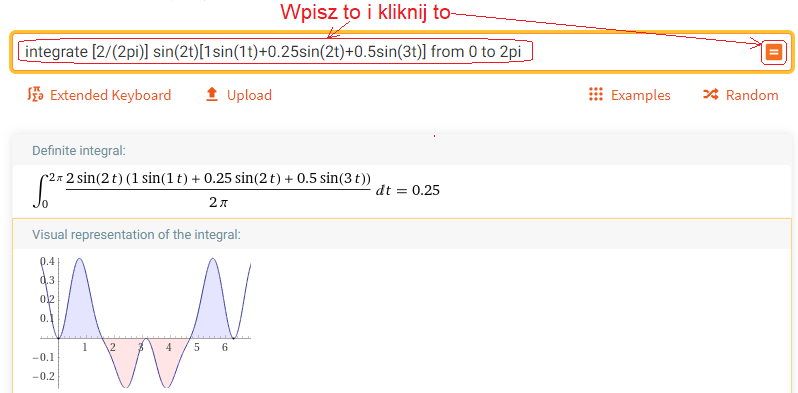

Rys. 2-7
Obliczanie b2– amplitudy drugiej harmonicznej
Zgadza się, b2=0.25. Pamiętaj, że pola “górne” i “dolne” odejmują się.

Rozdział 2.4.5  Amplituda trzeciej harmonicznej-b3
Wywołaj https://www.wolframalpha.com i rób co każe obrazek.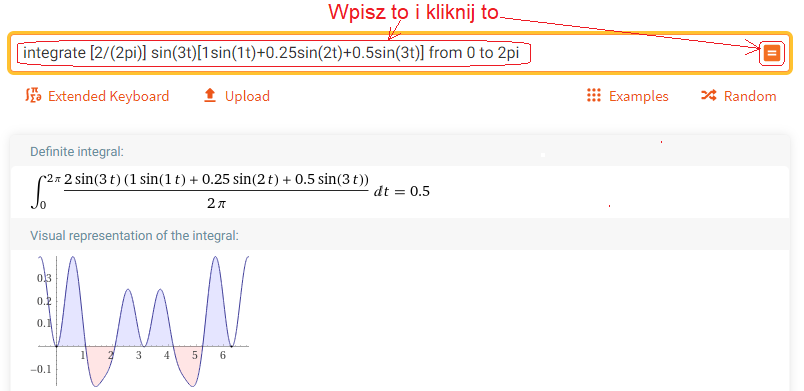

Rys. 2-8
Obliczanie b3– amplitudy trzeciej harmonicznej
Zgadza się, b3=0.5
Wnioski
Symulacje z rozdziałów 2.4.2…5 potwierdziły prawdziwość wzoru Rys. 2-4j

Rozdział 2.5 Funkcje ortogonalne
Rozdział 2.5.1
Wróć na chwilę do Rys. 2-4g z rozdziału 2.3. Tam dwie całki były zerowe a jedna miała wartość π. Teraz dowiesz się dlaczego?
Bo w tych zerowych były iloczyny funkcji ortogonalnych, a w tej z π iloczyny funkcji nieortogonalnych.

Rys. 2-9
Definicja funkcji ortogonalnych
Dla elektryka prąd i napięcie sinusoidalne na cewce są funkcjami ortogonalnymi bo energia w okresie T jest zerowa! Przez jedną połowę okresu cewka przyjmuję energię a przez drugą oddaje.
Będziemy badać ortogonalność różnych kombinacji par funkcji sin(nωt) i cos(kωt) dla Okaże się że:
Tylko kombinacje sin(nt)*sin(nt) i cos(nt)*cos(nt) nie są ortogonalne i ich całka=π
Pozostałe kombinacje sin(nt)*cos(kt) są ortogonalne i ich całka=0

Rozdział 2.5.2 Czy funkcje sin(t) i cos(t) są ortogonalne?
Szereg Fouriera wymaga umiejętności całkowania. Aby za głęboko nie wchodzić w matematykę, w jakieś funkcje pierwotne i inne całkowania przez części, znowu wykorzystamy wspaniały program www.wolframalpha.com.  Z samego całkowania wystarczy wiedza, że całka oznaczona jest polem pod funkcją.
Dla przykładu sprawdzimy czy funkcje sin(t) i cos(t) są ortogonalne.
Kliknij https://www.wolframalpha.com i rób co każe obrazek.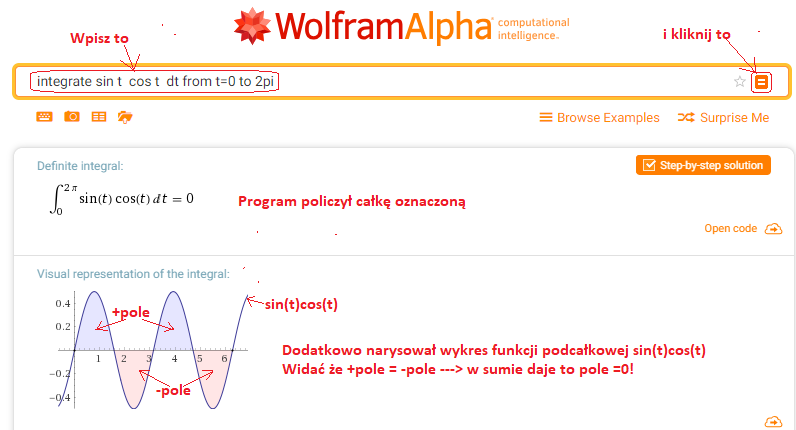

Rys. 2-10
Jak Wolfram Alfa sprawdził ortogonalność funkcji f1(t)=sin(t) i f2(t)=cos(t)?
Prościej i bardziej intuicyjnie już się nie da!
W następnych podrozdziałach sprawdzimy ortogonalność różnych kombinacji par sin(nωt) i cos(kωt).
Okaże się, że funkcje sin(nωt) i cos(kωt) są prawie zawsze ortogonalne oprócz par sin(nωt) i sin(nωt) oraz cos(nωt) i cos(nωt) których całki to T/2.

Rozdział 2.5.3 Pary sin(nωt) i cos(kωt) są ortogonalne
Wywołaj www.wolframalpha.com i sprawdź ortogonalność np. dla ω=1, n=2 i k=3 tj. dla f1(t)=sin(2t) i f2(t)=cos(3t)
W okno dialogowe zamiast “sin t cos t”  wpisz “sin 2t cos 3t”
Wolfram Allfa policzy da coś takiego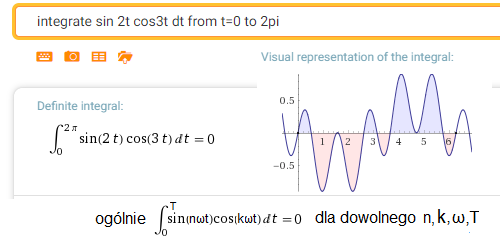

Rys. 2-11
Pary sin(nω) i cos(kω) są zawsze ortogonalne. Także dla n=k.
Uogólnienie na dowolne pary sin(nωt) i cos(kωt) pozostawiam matematykom. Uwaga ta dotyczy także następnych badanych par funkcji.
Uwaga.
Chociaż okresy funkcji sin(2t)=2π/ω=2π/2=π i sin(3t)=2π/3 są różne, to okres iloczynu sin(2t)sin(3t) równy jest okresowi funkcji sin(t) czyli 2π≈6.28. Widać to na Rys. 2-11! Spróbuj to udowodnić.
Generalnie to okres T funkcji sin(nωt)*cos(kωt) równy jest okresowi sin(ωt) czyli T=2π/ω.

Rozdział 2.5.4 Pary sin(nωt) i sin(kωt) oraz cos(nωt) i cos(kωt) dla n≠k są  ortogonalne
Proponuję samodzielnie sprawdzić Wolframem Alfa ortogonalność par funkcji sin(2t)sin(3t) i cos(2t)cos(3t)
Wynik powinien być następujący:

Rys. 2-12
Badanie ortogonalności par funkcji  sin(2t) i sin(3t) oraz cos(2t) i cos(3t) i ich uogólnienie.

Rozdział 2.5.5 Pary sin(nωt) i sin(nωt) oraz cos(nωt) i cos(nωt) nie są  ortogonalne!!!
Proponuję samodzielnie sprawdzić Wolframem Alfa ortogonalność par funkcji sin(2t)sin(2t) i cos(2t)cos(2t)
Wynik powinien być następujący:

Rys. 2-13
Badanie ortogonalności par funkcji  sin(2t) i sin(2t) oraz cos(2t) i cos(2t) i ich uogólnienie.
Funkcje nie są ortogonalne a ich całka= π dla ω=1 i ogólnie całka= T/2 (pół okresu) dla dowolnej pulsacji ω.

Rozdział 2.6 Jakie są parametry a0, a1, a2…an,,, b1,b2…bn Szeregu Fouriera?
Rozdział 2.6.1 Wstęp
Za chwilę przekonasz się jak bardzo ortogonalność ułatwia wyznaczanie Szeregu Fouriera.
Tak przy okazji. Ortogonalne czyli prostopadłe to mogą być wektory, ale funkcje?  W przestrzeniach Hilberta są podobno takowe a jak jest w naszych “ludzkich” przestrzeniach. Tu funkcje sin(ωt) i cos(ωt) kojarzą się z wirującymi wektorami z prędkością ω. Wektor cos(ωt)   wyprzedza wektor  sin(ωt) o 90º i oba wektory są wzajemnie prostopadłe. Inaczej funkcje sin(ωt) i cos(ωt) są ortogonalne.

Rozdział 2.6.2 Współczynnik a0
Jest to wartość średnia funkcji f(t) czyli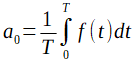

Rys. 2-14
Współczynnik a0 jako wartość średnia funkcji f(t) w okresie T

Rozdział 2.6.3 Współczynnik a2
Przypomina to trochę rozdział 2.3 o wyłuskiwaniu harmonicznych  Obliczmy np. współczynnik a2.

Rys. 2-15
Jak obliczyć współczynnik a2?
Rys. 2-15a Napisz wzór na szereg Fouriera z nieznanymi jeszcze współczynnikami. Wspólczynnik a0 już znamy.
Rys. 2-15b Pomnóż obie strony równania przez cos(2ωt) bo szukamy a2
Rys. 2-15c Oblicz całkę oznaczoną obu stron równania w zakresie 0…T
Rys. 2-15d Wartości całek zostały obliczone z powołaniem się na odpowiednie rysunki. Całka przy a0 jest zerowa jak to z cosinusem bywa.
Rys. 2-15e Po uwzględnieniu zer na Rys. 2-15d
Rys. 2-15f Ostateczny wzór na a2

Rozdział 2.7 Wyznaczenie Szeregu Fouriera
Przed chwilą wyznaczyliśmy współczynnik a2 Szeregu Fouriera. Podobnie  obliczymy dowolne an mnożąc obie strony równania z Rys. 2-15b przez cos(nωt) zamiast przez cos(2ωt). Natomiast jeżeli pomnożymy przez sin(nωt) to otrzymamy współczynnik bn. Uwzględniając jeszcze wzór na a0 z Rys. 2-14, ostateczny wzór na współczynniki a0,an i bn Szeregu Fouriera wygląda następująco: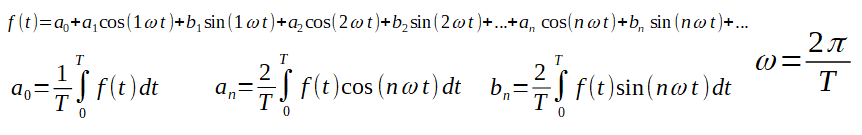

Rys. 2-16
Wzór na Szereg Fouriera
Zwróć uwagę na pulsację ω przebiegu funkcji okresowej f(t) i jej związek z okresem T.

Rozdział 2.8 Wyznaczenie Szeregu Fouriera dla fali prostokątnej
Rozdział 2.8.1 Szereg Fouriera fali prostokątnej bezpośrednio ze wzoru
Czyli dla przebiegu czasowego przedstawionego na wykresie.

Rys. 2-17
Fala prostokątna o okresie T=1 sek odpowiadająca pulsacji ω=2π/sek
Wyznaczmy  a0, a1,a2,…a7 i b1,b2,…b7.  Skorzystajmy ze wzoru ogólnego Rys. 2-16. Do obliczenia całek zastosujemy  program Wolfram Alfa. Rys. 2-18 to efekt obliczeń współczynników a0, a1 i b1. Bez bicia przyznam się do niewielkiej korekty-oszustwa. Program policzył a1 jako liczbę niewyobrażalnie małą, ale jednak różną od 0 zaś b1 jako 1.27324 a nie tak jako matematyka rzecze b1=4/π. Tę niedoskonałość poprawiłem, także dla pozostałych współczynników.

Rys. 2-18
Obliczenie a0, a1 i b1 dla Szeregu Fouriera fali prostokątnej z Rys 2-17
Pozostałe współczynniki a2, a3,a4,a5,a7 i b2,b3,b4,b5,b7 też oblicz Wolframem. Wystarczy tylko wpisać do okna dialogowego w miejsce “2 w czerwonej obwódce” odpowiednio 4,6,8,10,12 i 14.  Powinna powstać następująca tabelka.

Rys. 2-19
Współczynniki a0,a2, a3,a4,a5,a7 i b1,b2,b3,b4,b5,b7 Szeregu Fouriera fali prostokątnej z Rys. 2-17
Przy okazji. Badana funkcja jest nieparzystą i dlatego wszystkie współczynniki a1, a2, a3… są zerowe. Gdyby była parzystą (np. przesunięta w lewo o 0.25) to współczynniki b1, b2, b3… byłyby zerowe  natomiast a1, a2, a3…niezerowe. Jest to zgodne z intuicją.
Zróbmy wykres korzystając z programu http://pl.easima.com

Rys. 2-20
Rozkład fali prostokątnej na 4  harmoniczne.
A właściwie 7 pierwszych, bo b2=b4=b6=0. Pulsacją pierwszej harmonicznej jest ω=2π. Odpowiada jej okres T=1. Im więcej harmonicznych, tym bardziej ich suma zbliżona jest do fali prostokątnej.

Rozdział 2.8.2 Szereg Fouriera fali prostokątnej korzystając ze specjalnych funkcji programu Wolfram Alfa
Poprzednio wyznaczyliśmy 7 harmonicznych fali prostokątnej korzystając z ogólnych instrukcji całkowania programu Wolframu Alfa. Program dysponuje też wyspecjalizowanymi instrukcjami do wyznaczania Szeregu Fouriera. Wystarczy tylko wpisać je do okna dialogowego a on to policzy i zrobi wykres! Nawet nie musisz znać się na całkach.
Sprawdźmy Wolfram Alfa dla tej samej fali prostokątnej. Efekt powinien być identyczny.
Nie wchodźmy w szczegóły instrukcji wpisanej do okna dialogowego. Niech wystarczy nam tylko wiedza, że liczy ona parametry Szeregu Fouriera dla fali prostokątnej o parametrach z Rys. 2-17. Policzy nam 7 pierwszych harmonicznych. Gdybyś chciał ich policzyć np. 9  to zamiast 7 wpisz właśnie 9.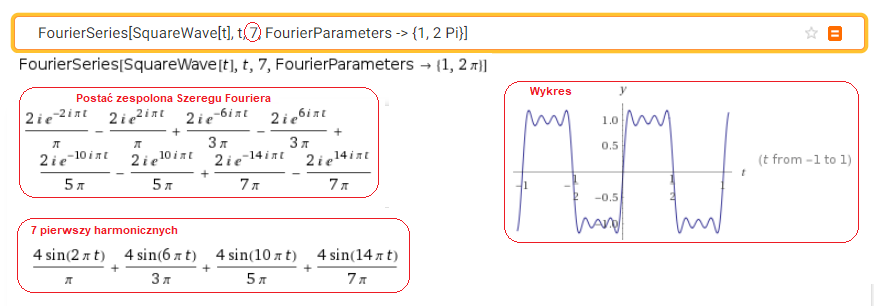

Rys. 2-21
Rozkład fali prostokątnej z Rys. 2-17 na 7 harmonicznych
Program pokaże nam dużo różnych rzeczy. Na Rys. 2-21 są tylko te najbardziej istotne. Postać Zespolona Szeregu Fouriera ujęta będzie w Rozdziale 4. Ważne jest to, że wykres i współczynniki  są dokładnie takie same jak na Rys. 2-20. A o ile mniej roboty!
To sprawdźmy jeszcze to cudo do wyznaczenia  9 pierwszych harmonicznych.

Rys. 2-22
Rozkład fali prostokątnej z Rys. 2-13 na 9 harmonicznych
Jest to dokładniejsze przybliżenie fali prostokątnej.
To może np. 17 harmonicznych? Powinno być jeszcze dokładniejsze przybliżenie.

Rys. 2-23
Rozkład fali prostokątnej z Rys. 2-17 na 17 harmonicznych
Wykres dokładniej odzwierciedla falę prostokątną. Nie wyznaczył nam niestety trygonometrycznej wersji Szeregu Fouriera jak poprzednio. Nie jest to wielkim mankamentem, bo odpowiednie  parametry można odczytać z postaci zespolonej.ć
Przy próbie wyznaczenia 19 i więcej harmonicznych program Wolfram Alfa już nie wyrabia. Podejrzewam, że ma jednak jakieś specjalne furtki. Może płatny Wolfram Alfa Pro da radę?
Przeregulowanie na początku kążdego impulsu to tzw. efekt Gibsa.  Pojawia się gdy n ma wartość skończoną a znika gdy n=∞.

Rozdział 2.9 Wyznaczenie Szeregu Fouriera dla innych funkcji okresowych
Rozdział 2.9.1 Funkcja 1sin(t)
Ciekawe jak zachowa się  Wolframik przy tak trywialnej funkcji?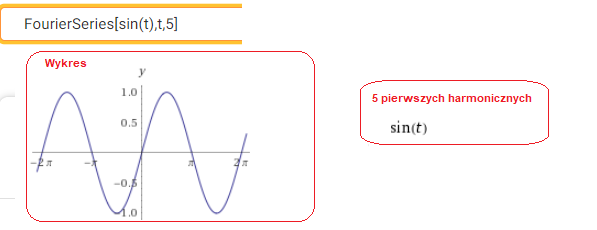

Rys. 2-24
Rozkład sin(t) na 5 harmonicznych.
Powyższa instrukcja dotyczy rozkładu funkcji okresowej (tu  sin(t)) na 5 harmonicznych przy dodatkowym założeniu że T=2π czyli ω=1.
Jest oczywiste, że pierwszą harmoniczną jest ta sama funkcja, czyli sin(t) a pozostałe harmoniczne nie istnieją, albo inaczej ich amplitudy są zerowe. Milczące założenie T=2π czyli ω=1 dotyczy także następnych przykładów.

Rozdział 2.9.2 “Piła” czyli funkcja t
Przypominam, że jest to funkcja okresowa o T=2π

Rys. 2-25
Rozkład “piły” czyli funkcji t  na 5 i 9 harmonicznych.
Przybliżenie “piły”  9 harmonicznymi jest oczywiście dokładniejsze.

Rozdział 2.9.3 Funkcja kwadratowa czyli funkcja t^2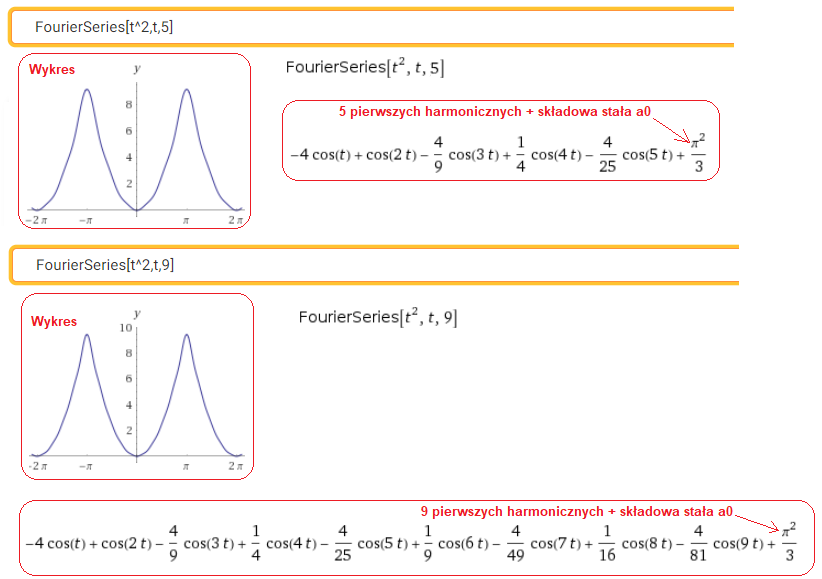

Rys. 2-26
Rozkład funkcji kwadratowej na 5 i 9 harmonicznych. Zauważ, że w zakresie -π…+π przybliżenie 9 harmonicznymi wizualnie nie różni się od funkcji kwadratowej. Przy okazji dowiedzieliśmy się, że istnieje coś takiego jak składowa stała a0. W poprzednich przykładach jej nie było.