Podstawy Automatyki

Rozdz. 15 Więcej o Transmitancji i Łączenie Bloków
Rozdz. 15.1 Wstęp
Transmitancję obiektu dynamicznego G(s) pozwala nam wyznaczyć sygnał wyjściowy y(t) gdy znamy sygnał wejściowy x(t). Przypadek najprostszy to człon proporcjonalny – np. idealny wzmacniacz o wzmocnieniu k=10. Dla niego G(s)=k=10. Tu G(s) w banalny sposób łączy y(t) z x(t) równaniem y(t)=k*x(t) 
np. y(t)=10*sin(t) gdy x(t)=sin(t). Niestety, prawdziwe obiekty dynamiczne zawierają w sobie bezwładności. Coś co powoduje, że nic nie dzieje się natychmiast. Jeśli naciskasz pedał gazu w samochodzie, to nigdy nie nastąpi skok prędkości z zera do np. 10 km/godz. Wtedy przyspieszenie urwałoby łeb z płucami. Prędkość zwiększa się stopniowo, aż osiągnie te swoje 10 km/godz.
Z oczywistych powodów transmitancji nie możemy zdefiniować jako zwykły iloraz y(t)/x(t). Nie byłoby czegoś stałego, (jak w G(s)=10 dla członu proporcjonalnego). Problem da się rozwiązać, ale tylko wtedy gdy bierzemy pod uwagę nie przebiegi x(t) i y(t), ale ich transformaty Laplace’a X(s) i Y(s) tak jak na rysunku.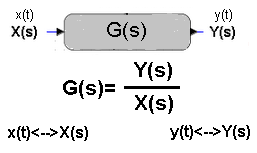

Rys. 15-1
Transmitancja G(s) jako stosunek dwóch transformat.

Rozdz. 15.2 Transmitancja a równanie różniczkowe na przykładzie członu inercyjnego
Najprostszym ale niebanalnym, bo opisanym już przez równanie różniczkowe, jest człon inercyjny np. o stałej czasowej T=1 sek i K=1. Zbadamy odpowiedź na skok jednostkowy x(t)=1(t) i sprawdzimy, czy będzie zgodna z rozwiązaniem równania różniczkowego.

Rys. 15-2
Jest to typowa odpowiedź członu inercyjnego o K=1 i T=1 sek. Na razie nie zwracaj uwagi na równanie na wykresie opisujące y(t). Do tej pory człon inercyjny G(s) to jest „coś” z Rys. 15-2, co na skok jednostkowy x(t)=1(t) reagowało przebiegiem z Rys. 15-3.
Jesteś też w stanie przewidzieć, jak inne inercyjne „coś” np.

Rys. 15-3
zareaguje na skok jednostkowy –>Rozdz. 3 Rys.3-6.
W ten sposób mając transmitancję G(s) intuicyjnie kojarzysz x(t) i y(t), czyli z przebiegami czasowymi. Apeluję o szersze spojrzenie.
W transmitancji G(s) jest ukryte równanie różniczkowe!
Wróćmy na chwilę do zbiornika z dziurą Rozdział 13.3.
Tu wyjście y(t) związane jest z wejściem x(t) równaniem różniczkowym x(t) = y'(t) + y(t) opisujące napełnianie zbiornika z dziurą . Rozwiążemy je korzystając z rachunku operatorowego. Obie strony tego równania poddamy przekształceniu operatorowemu s. Możemy tak zrobić, bo wiemy, że każdej funkcji czasowej f(t) odpowiada papużka nierozłączka F(s). Odwrotnie też. Zapisujemy to tak f(t)<=>F(s). Jak każdej funkcji f(t), to także każdej funkcji x(t) i y(t).
Czyli
x(t)=y'(t)+y(t)
x(t)<=>X(s) tu x(t)=1(t) (skok jednostkowy)
y(t)<=>Y(s)
y'(t)<=>sY(s)
W ostatnim przekształceniu wykorzystaliśmy wspaniałą właściwość rachunku operatorowego, że transformata pochodnej f(t) to s*F(s). Gdyby rachunek operatorowy nie miał tego cuda, to byłby po prostu bezużyteczny.
W ten sposób równanie różniczkowe
x(t)=y'(t)+y(t)
przekształciliśmy na równanie operatorowe
X(s)=s*Y(s)+Y(s)
Ostatnie równanie można zapisać tak: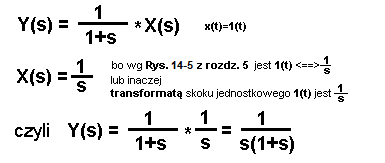

Rys. 15-4
Znamy już transformatę Y(s). Wystarczy tylko znaleźć mądrej książce drugą papużkę nierozłączkę
pary y(t)<—>Y(s), czyli y(t).
Od czego zacząć? Chyba od Rys. 14-5 rozdz. 14 , gdzie jest kawałek mądrej książki. Jest tam co prawda tylko kilka par, ale mamy farta, bo znaleźliśmy interesującą nas parę f(t)<–>F(s).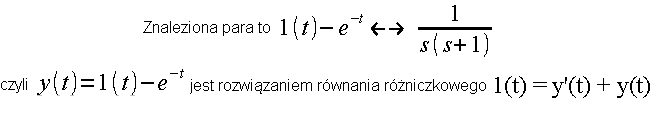

Rys. 15-5
Przypominam, że e=2.71828… jest jedną z najważniejszych liczb w matematyce. Wyjście y(t) zostało obliczone jako rozwiązania równania różniczkowego opisującą transmitancję G(s) z Rys. 15-2, czyli czysta teoria. To samo zrobił Xcos na Rys. 15-2. Czyli linia powinna pokrywać się z wartościami y(t).
Sprawdźmy dla np. t=0 sek, t=1 sek i t=7 sek.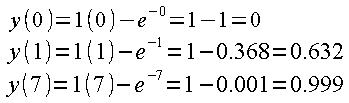

Rys. 15-6
Zgadza się!!!

Rozdz. 15.3 Transmitancja a równanie różniczkowe dla dowolnego członu
Wykazaliśmy już , że obiektowi opisanemu prostym równaniem różniczkowym
x(t)=y'(t)+y(t)
odpowiada transmitancja G(s) członu inercyjnego o parametrach k=1 i T=1 sek.
Poniższy rysunek pokazuje jak tworzona jest transmitancja przy bardziej skomplikowanym równaniu różniczkowym np.3 stopnia.
W sposób analogiczny będzie tworzona transmitancja na podstawie równania różniczkowego dowolnego stopnia

Rys. 15-7
Widzimy więc, że transmitancja G(s) jest ilorazem gdzie licznik L(s) i mianownik M(s) to wielomiany odpowiednich stopni. Przeważnie L(s) ma niższy stopień niż M(s) a najczęściej to tylko L(s)=bo, w dodatku bo=1 a mianownik jest iloczynem wielomianów pierwszego lub drugiego stopnia.
Np. człon dwuinercyjny ma w mianowniku 2 wielomiany pierwszego stopnia
M(s)=(1+s*T1)*(1+s*T2)
Sprawdźmy odpowiedź na skok transmitancji z Rys. 15-7 przy konkretnych parametrach mianownika M(s) i licznika L(s).
M(s)–> a0,a1,a2,a3
L(s)–> b0,b1,b2,b3

Rys. 15-8
Widzimy jak wyższe pochodne mieszają w przebiegu czasowym. Zwłaszcza, że współczynniki przy tych pochodnych są małe. A co by było gdyby były duże. Strach pomyśleć!
Dla większości transmitancji łatwo można wyznaczyć wzmocnienie K w stanie ustalonym. Jest to po prostu wyraz wolny bo w liczniku transmitancji, przy założeniu że wyraz wolny w mianowniku ao=1. Jeżeli ao jest różne od 1 to podziel licznik i mianownik przez ao.
Oczywiście tak jest, gdy G(s) dotyczy układów stabilnych. Nie takich w których dowolne zakłócenie powoduje, że G(s) staje się generatorem. Sporo wiesz o odpowiedzi transmitancji G(s) skok jednostkowy 1(t).
Wyjście y(t=2)=0, co jest oczywiste.
Oraz w stanie ustalonym y(t)=bo=K.
A za to co się dzieje w stanie przejściowym („pomiędzy”), czyli dla t=2…15sek sek odpowiadają pozostałe parametry transmitancji przy s.
Są to współczynniki a1, a2, a3 i b1, b2, b3, których konkretne wartości widoczne są w transmitancji G(s) na Rys. 15-8.

Rozdz. 15.4 Transmitancja wypadkowa czyli łączenie transmitancji
Bloki można łączyć metodą:
– szeregową
– równoległą
– ze sprzężeniem zwrotnym
Możliwe też są kombinacje tych metod.

Rozdz. 15.5 Szeregowe łączenie bloków

Rys. 15-9
Jest to połączenie szeregowe dwóch bloków inercyjnych G1(s) i G2(s) .
Przykład masz w domu. Najpierw gorąca woda (chyba 70°C) jest doprowadzona do kaloryfera który stosunkowo szybko się nagrzeje, potem kaloryfer nagrzeje pokój, a ściślej miejsce w pokoju w którym umieszczony jest termometr. Pierwsza stała czasowa jest mała – kilka minut, druga duża- więcej minut. Dokładniejszy model uwzględniałby jeszcze opóźnienie To.
Nie chcę żeby eksperyment trwał półtorej godziny. Dlatego nasz model ma dużo mniejsze stałe czasowe T1=3 sek i T2=5 sek.
– Sygnałem wejściowym jest skok x(t)
– pośrednim y1(t) typowa inercja – wyjściowym y(t) typowy dwuinercyjny z charakterystycznym punktem przegięcia. Chyba zgodne z intuicją.
Zwłaszcza że:
– biorąc pod uwagę „ociężałość” 2 szeregowo połączonych członów inercyjnych w stanie przejściowym powinno być y1(t)>y(t)
– w stanie ustalonym y(t)=y1(t)=x(t)
Potwierdzają to przebiegi.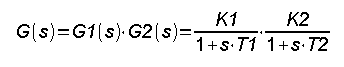

Rys. 15-10
Transmitancja wypadkowa G(s) bloków połączonych szeregowo jest iloczynem ich transmitancji G1(s) i G1(s). Wzór ten jest najbardziej oczywisty dla członów proporcjonalnych np. wzmacniaczy, których wzmocnienie jest iloczynem wzmocnień K=K1*K2. Na Rys. 15-9 były to 2 transmitancje inercyjne o parametrach K1=1, T1=3 sek i K2=1, T2=5 sek.

Rozdz. 15.6 Równoległe łączenie bloków

Rys. 15-11
W połączeniu równoległym sygnał wejściowy x(t) „rozcapierza” się z jednego węzła zaczepowego na 2 wejścia bloków inercyjnych. Potem wyjścia tych bloków y1(t) i y2(t) sumują się w węźle sumacyjnym. Z przebiegów wyraźnie wynika, że wyjście jest sumą wyjść dwóch bloków, co przekłada się na to, że transmitancja wypadkowa jest sumą poszczególnych transmitancji.
Uwaga na marginesie.
Przebieg y(t) wygląda jak dla typowego członu inercyjnego. Spróbuj jednak dodać 2 ułamki G(s)=G1(s)+G2(s). Nie wyjdzie człon inercyjny ani nawet dwuinercyjny. Pojawią się jakieś s-y w liczniku L(s) transmitancji wypadkowej G(s).
Pamiętaj!
Na wejściu jest zawsze węzeł zaczepowy a na wyjściu sumacyjny! Gdyby na wyjściu też był zaczepowy, to tak jakbyś połączył równoległe wyjścia 2  różnych napięć.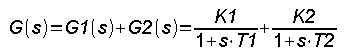

Rys. 15-12
Transmitancja wypadkowa G(s) jest sumą G1(s) i G2(s). U nas były to 2 transmitancje inercyjne o parametrach K1=0.5, T1=3 sek i K2=0.5, T2=5 sek . Dla członów proporcjonalnych np. wzmacniaczy transmitancja czyli wzmocnienie też jest sumą wzmocnień K=K1+K2.

Rozdz. 15.7 Połączenie z ujemnym sprzężeniem zwrotnym
Połączenie szeregowe i równoległe łatwo poddaje się intuicji. Inaczej jest z ujemnym sprzężeniem zwrotnym. Nie bardzo wiadomo co jest przyczyną a co skutkiem. Właściwie cała automatyka to są ujemne sprzężenia zwrotne, w tej albo innej formie. Na razie potraktujmy sprzężenie zwrotne beznamiętnie-czysto matematycznie przy pomocy rachunku operatorowego. Mając transmitancję układu otwartego G(s) obliczmy transmitancję układu zamkniętego Gz(s)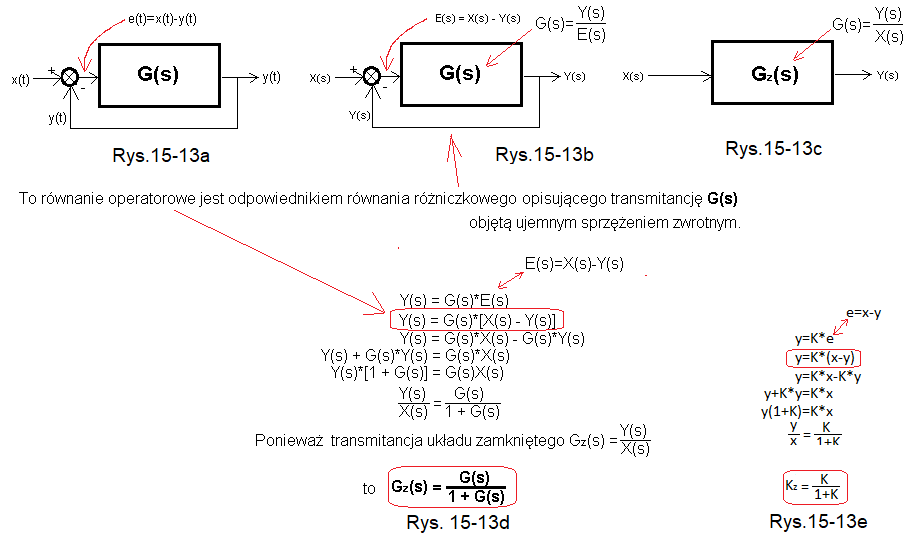

Rys. 15-13
Ujemne sprzężenie zwrotne powstało po wprowadzeniu na wejście układu otwartego G(s) różnicy sygnałów e(t)=x(t)-y(t). Sygnał wyjściowy y(t) został ponownie wprowadzony (zwrócony!) na wejście G(s) z ujemnym znakiem tak jak na Rys. 19-17a.
Stąd ta nazwa-Układ z Ujemnym Sprzężeniem Zwrotnym.
Ludzie już dawno zauważyli, że taka struktura daje sporo korzyści. Np. sygnał wyjściowy y(t) stara się naśladować sygnał wejściowy x(t) niezależnie od zakłóceń. Druga korzyść to możliwość przyspieszenia działania urządzenia.
Rys. 15-13a przedstawia tory sygnałowe transmitancji w funkcji czasu t transmitancji G(s), która jest zamknięta pętlą ujemnego sprzężenia zwrotnego.
Rys. 15-13b powstał poprzez przekształcenie sygnałów czasowych na Rys. 19-17a na odpowiednie transformaty Laplace’a.
Rys. 15-13c Transmitancją każdego układu to jest stosunek Y(s)/X(s). Dlatego transmitancją układu zamkniętego jest Gz(s).
Rys. 15-13d Wyprowadzenie wzoru na transmitancję układu zamkniętego Gz(s).
Rys. 15-13e Wyprowadzenie wzoru na wzmocnienie układu zamkniętego Kz w stanie ustalonym. Wzór ten najłatwiej wyprowadzić jako Kz=Gz(0), czyli podstawiając s=0 do wzoru Rys. 15-13d. Ale poszliśmy inną drogą. Wyszliśmy z bardzo ważnej obserwacji, że w stanie ustalonym y(t)=K*e(t). Dla wielu jest to oczywiste, ale z drugiej strony ta zasada jest tak ważna, że postaram się to uzasadnić w następnym rozdziale. Ponieważ w stanie ustalonym sygnały są stałe–>x(t)=x i y(t)=y, to łatwo dojedziemy do wzoru na Kz. Sprawdźmy jeszcze, czy wyprowadzony wzór na Gz(s) jest prawdziwy dla jakiejś konkretnej transmitancji G(s).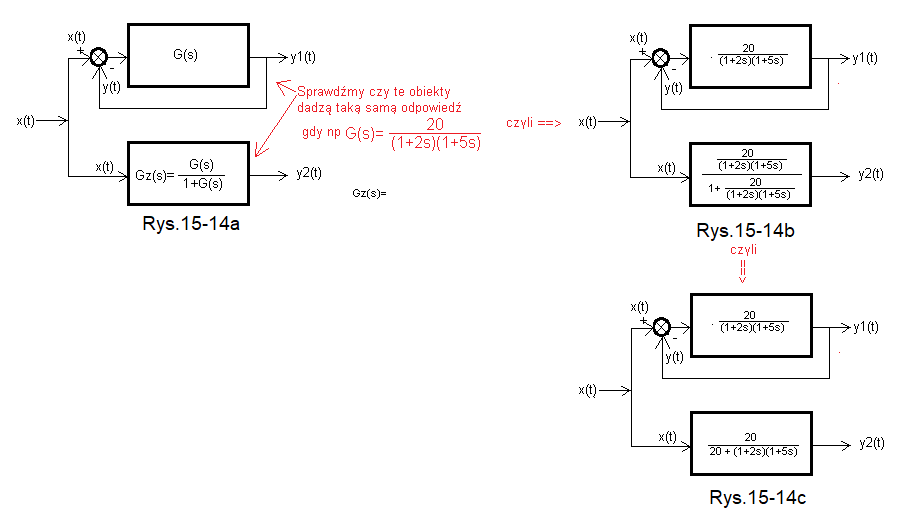

Rys. 15-14
Konkretna transmitancja G(s) to człon dwuinercyjny o parametrach K=20, T1=2 sek, T2=5 sek.
Górny Rys. 15-14a to G(s) objęte ujemnym sprzężeniem zwrotnym, a dolny Rys. 15-14a to transmitancja zastępcza Gz(s) górnego zgodna z wyprowadzonym wzorem na Rys. 15-13.
Rys. 15-14b to realizacja 15-14a dla naszej konkretnej transmitancji a Rys. 15-14c to jest to samo po elementarnych przekształceniach.
Na wejścia górnych i dolnych bloków wchodzi ten sam skok jednostkowy x(t), tak że spodziewamy się takich samych odpowiedzi y1(t)=y2(t).
Czy tak będzie?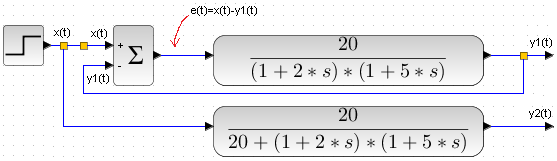

Rys. 15-15
Schemat dokładnie odpowiada Rys. 15-14c.

Rys. 15-16
Układ z ujemnym sprzężeniem zwrotnym i jego transmitancja zastępcza dają taką samą odpowiedź na x(t).
Zwróć uwagę na wzmocnienie Kz w stanie ustalonym. Czy nie kojarzy się ze wzorem na transmitancję układu zastępczego Gz(s)? Poza tym, sygnał y(t) w stanie ustalonym jest prawie równy sygnałowi x(t)! Czyli sygnał wyjściowy y(t) stara się naśladować sygnał wejściowy x(t). Tak jak pracownik stara się wykonywać polecenia kierownika.
To było tylko dość suche i matematyczne wprowadzenie do sprzężenia zwrotnego.
Dlatego cały następny Rozdział 16 dotyczy tylko tego tematu.

Rozdz. 15.8 Wnioski
1. Transmitancja G(s) jest odpowiednikiem równania różniczkowego opisującego dany obiekt dynamiczny
2. Z parametrów G(s) łatwo wyznaczymy wzmocnienie K w stanie ustalonym–>Rys. 15-8
3. Na Rys. 19-8 i Rys. 19-9 transmitancje G(s) podane były jako „gołe” ilorazy gdzie licznik i mianownik był klasyczną postacią wielomianu. Często podaje się je w nieco przekształconej formie jak np.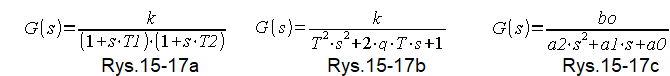

Rys. 15-17
Sprawa jest prosta. Tu już na pierwszy rzut oka widać, że mamy do czynienia z członem dwuinercyjnym o parametrach k,T1,T2–>Rys.15-17a albo z członem oscylacyjnym o parametrach k,T,q–>Rys.15-17b . Tego nie byłoby widać w „gołym” ilorazie Rys. 15-17c
4. Transmitancje bloków połączonych:
-szeregowo
-równolegle
-z ujemnym sprzężeniem zwrotnym
można zastąpić pojedynczą transmitancją zastępczą