Wirujące Szeregi Fouriera

Rozdział 8. Szereg Fouriera fali prostokątnej parzystej.

Rozdział 8.1 Wstęp
Do tej pory badaliśmy funkcje f(t), w której wszystkie harmoniczne były widoczne we wzorze np. f(t)=1.3+0.7cos(2t)+05.cos(4t).
A wszystko to, jakby powiedział Michał Wiśniewski, w celu sprawdzenia wzorów Fouriera. A gdy harmonicznych nie widać w funkcji f(t)?
Tak jak np. w fali prostokątnej f(t) o amplitudzie A=1, pulsacji  ω=1/sek i fazie początkowej ϕ=0 i wypełnieniu w=50%.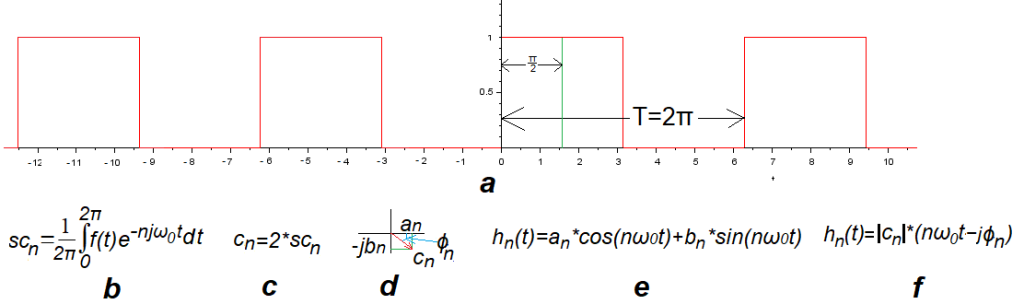

Rys.8-1
Fala prostokątna parzysta i wzory na harmoniczne
Rys.8-1a
Fala prostokątna parzysta f(t)  A=1, ω=1/sek, ϕ=0 i w=50%.
Kilka słów wyjaśnienia. Parametry A, ω i ϕ są typowe dla funkcji trygonometrycznych. Trudno je przypisać np. funkcji kwadratowej. Ale fali prostokątnej już tak! Parametry  A=1 i ω=1/sek są oczywiste. Dodam tylko, że ω=1/sek odpowiada okresowi T=2πsek. Zaś ϕ=0 oznacza, że fala zaczyna się w “górnej połówce prostokąta”, tak jak  ϕ=0 w “górnej połówce cosinusoidy”.
Wzory na harmoniczne
W następnych punktach będziemy analizować trajektorie F(n*jω0t) i wykresy czasowe fali prostokątnej dla n=0…8. Podobnie jak poprzednio robiliśmy to z funkcjami trygonometrycznymi. Ale najpierw kilka słów jak ze środka ciężkości n-tej trajektorii F(njω0t) odczytać n-tą harmoniczną hn(t).
Rys.8-1b
Wzór na n-ty środek ciężkości scn trajektorii F(n*jω0t)
W tym rozdziale środki ciężkości scn zgadzają się z intuicją i tylko założymy, że są prawdziwe. W rozdziale 11 obliczymy je dokładnie programem WolframAlfa.
Rys.8-1c
Wzór na n-ty zespolony współczynnik szeregu Fouriera cn
Jest to po podwojony środek ciężkości scn!  Traktuj to jako zespoloną amplitudę dla n-tej harmonicznej.
Uwaga
Wzór jest prawdziwy dla n=1,2,3…
Dla n=0
c0=sc0=a0 i jest to średnia f(t) w okresie 0…2π. Podstaw n=0 to powstanie całka jako wzór Rys.7-2c z rozdz. 7.
Rys.8-1d
cn  jako zespolona amplituda:
cn=an+jbn  w wersji algebraicznej  
cn=|cn|exp(jϕ) w wersji wykładniczej gdzie:
-|cn| moduł amplitudy obliczany “Pitagorasem z an i bn”
-ϕ faza jako an/bn=tg(ϕ)
Rys.8-1e
Wzór na n-tą harmoniczną hn(t) o składowych cosinus/sinus
Rys.8-1f
Wzór na n-tą harmoniczną hn(t) jako cosinus z przesunięciem fazowym ϕ.
Uwaga
Temat powyższych wzorów został omówiony w p7.2 rozdz. 7

Rozdział 8.2 Fala prostokątna parzysta f(t) i jej trajektoria F(njω0t) dla n=0 czyli F(0j1t)

Rys.8-2
Trajektoria F(0j1) funkcji f(t) fali prostokątnej parzystej, czyli  o parametrach:
A=1-amplltuda
ω0=1/sek-pulsacja odpowiadająca okresowi T=2πsek≈6.28sek.
ϕ=0 
50%-wypełnienie
Rys.8-2a
Trajektoria F(0j1t) odpowiadająca trajektorii F(njω0t) dla n=0 i ω0=1/sek.
Nieruchoma płaszczyzna Z, gdzie na osi rzeczywistej Re Z  wektor zmienia się wg. funkcji f(t) pokazanej na Rys.8-2b. Innymi słowy są to skokowe ruchy “w te i we wte” na osi rzeczywistej Re Z między punktami (0,0) i (1,0).
Rys.8-2b
Wykres czasowy f(t) fali prostokątnej parzystej. Zauważ, że przebieg rozpoczyna się w połowie półokresu. Podobnie jak funkcja cosinus.
Obydwie animacje z Rys. a i b opisują to samo. Odczytaj parametry A,ω0,ϕ i wypełnienie. Z animacji b jest łatwiej, ale z a też się da.
Z wykresu można obliczyć, nawet bez całek współczynnik c0=a0=0.5 Szeregu Fouriera jako wartość średnią f(t) dla 0…2π. Patrz Rys.8-1c.
W następnych podrozdziałach  płaszczyzna Z zacznie obracać się z prędkościami ω= -nω0, czyli z -1/sek,-2/sek…-8/sek w kierunku “zegarowym”. Koniec wektora będzie rysował trajektorie F(njω0). Z nich odczytamy harmoniczne dla  pulsacji nω0. Tak jak w poprzednich rozdziałach, tylko zamiast f(t)=kombinacja sinusów i cosinusów, teraz będzie f(t)=fala prostokątna.

Rozdział 8.3 Pierwsza harmoniczna fali prostokątnej parzystej h1(t) =a1*cos(1t).
Rozdział 8.3.1 Trajektoria F(njω0t) fali prostokątnej parzystej dla n=1 i ω0=1/sek, czyli F(1j1t).

Rys.8-3
Trajektoria F(1j1t) fali prostokątnej parzystej
Rys.8-3a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-1/sek wokół punktu (0,0) w czasie T=2π sek. Wraz z nim obraca się cała płaszczyzna zespolona  Z. Ale uwaga! Osie płaszczyzny Re Z i Im Z stoją w miejscu! Koniec wektora narysowałby cały okrąg w odróżnieniu od półokręgu na Rys.8-3c. Średnią wartością sumy obracających się wektorów w czasie 1  obrotu, czyli w czasie 2π sek jest wektor zerowy z=(0,0). Parametr z to tzw. środek ciężkości trajektorii, czyli okręgu. Tu akurat z pokrywa się ze środkiem ciężkości sc znanym z fizyki.
Rys.8-3b
Trajektoria F(1j1t)=f(t)*exp(-1j1t) jako  wirujący wektor modulowany funkcją f(t). Funkcja f(t) jest  falą prostokątną z Rys.8-2b.
Spójrz na Rys.8-2a i wyobraź sobie, że płaszczyzna Z zacznie się obracać z prędkością ω=-1/sek. Przypominam, że osie Re Z i Im Z są nieruchome! W ten sposób powstanie wirujący wektor F(1j1t)=f(t)*exp(-1j1t). Płaszczyzna Z wykona 1 obrót, zaś promień R=1 zrobi 2 “ćwierćobroty” z przerwą 1π sek pomiędzy. Jest to równoważne jednemu “półobrotowi”.
Rys.8-3c
Trajektoria F(1j1t) jako półokrąg rysowany przez koniec wektora z Rys.8-3b.
A teraz wyobraź sobie, że w czasie 1 obrotu płaszczyzny Z, czyli o kąt 0…2π wszystkie wektory są sumowane (wektorowo!) i obliczana jest ich średnia. Powstanie jakiś wektor sc1. Czy będzie to sc1=(0,0) jak dla Rys.8-3a? Chyba nie, ale na pewno będzie leżał gdzieś na osi Re Z między (0,0) a (1,0). Raczej bliżej (0,0) niż (1,0). Będzie nim wektor sc1=(1/π, 0)! Inaczej środek ciężkości sc1=(1/π, 0) trajektorii F(1j1t). Parametr sc1 trajektorii dokładnie obliczymy programem WolframAlfa  w rozdziale 11.
Uwaga do Rys 8-3b,c
Powyższe animacje sugerują, że górne i dolne “ćwiartki” trajektorii są rozdzielone przerwą T=π sek. Ale tak jest tylko na początku w czasie t=0…2π sek! Później nie ma tej przerwy i ruch po trajektorii jest ciągły.

Rozdział 8.3.2 Pierwsza harmoniczna na tle fali prostokątnej parzystej czyli c0+h1(t) albo inaczej  pierwsze przybliżenie fali prostokątnej parzystej.
Wg Rys. 8-1c
Składowa stała c0 to średnia w okresie T=2π czyli c0=a0=0.5 . Obliczysz to nawet bez rachunku całkowego.
c1 jest amplitudą zespoloną pierwszej harmonicznej
c1=2*sc1=(2/π,0) czyli a1=2/π i b1=0
Wg Rys. 8-1e
h1(t)=(2/π)*cos(1t)≈0.637cos(1t)

Rys.8-4
S1(t)=c0+h1(t) czyli pierwsza harmoniczna  ze składową stałą c0=0.5 na tle fali prostokątnej.
Jest to także pierwsze przybliżenie naszej fali prostokątnej parzystej 50%.

Rozdział 8.4 Druga harmoniczna fali prostokątnej parzystej, a właściwie jej brak bo c2=0 –>h2(t)=a2*cos(2t)=0.
Rozdział 8.4.1 Trajektoria F(njω0t) fali prostokątnej parzystej dla n=2 i ω0=1/sek, czyli F(2j1t).
Płaszczyzna Z obraca się z prędkością ω=-2/sek

Rys.8-5
Trajektoria F(2j1t) fali prostokątnej parzystej
Rys.8-5a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-2/sek wokół punktu (0,0) i wykona 2 obroty w czasie T=2π sek.
Rys.8-5b
Trajektoria F(2j1t)=f(t)*exp(-2j1t) jako  wirujący wektor modulowany funkcją f(t).
W czasie 2π sek płaszczyzna Z wykona 2 obroty, ale promień R=1 zrobi tylko 2 “półobroty” z przerwą 1π sek pomiędzy.
Rys.8-5c
Trajektoria F(2j1t) jako okrąg rysowany przez koniec wektora z Rys.8-3b.
Ewidentnie sc2=0. Zauważ, że z samego okręgu wartość sc2=0 nie jest oczywista! Przecież okrąg mógł być narysowany np. 1.5 razy. Na szczęście ten 1 pełny obrót, choć z przerwą w środku, jest widoczny na Rys.8-5b
Wniosek
sc2=0 i dlatego harmoniczna dla ω=2/sek nie istnieje.

Rozdział 8.5 Trzecia harmoniczna symetrycznej fali prostokątnej parzystej h3(t) =a3*cos(3t).
Rozdział 8.5.1 Trajektoria F(njω0t) fali prostokątnej parzystej dla n=3 i ω0=1/sek, czyli F(3j1t).
Płaszczyzna Z obraca się z prędkością ω=-3/sek

Rys.8-6
Trajektoria F(3j1t) fali prostokątnej parzystej
Rys.8-6a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-3/sek wokół punktu (0,0) i wykona 3 obroty w czasie T=2π sek.
Rys.8-6b
Trajektoria F(3j1t)=f(t)*exp(-3j1t) jako  wirujący wektor modulowany funkcją f(t).
W czasie T=2π sek płaszczyzna Z wykona 3 obroty, ale promień R=1 tylko 2 razy “3/4obrotu” z przerwą 1π sek pomiędzy. Okaże się,  że w czasie T=2π sek promień R=1 dłużej przebywa na lewej półpłaszczyźnie niż na prawej. Dlatego jego średnia wartość jako wektor będzie (-1/3π, 0) 
Rys.8-6c
Trajektoria F(3j1t) jako okrąg rysowany przez koniec wektora z Rys.8-6b.
Środek ciężkości sc3=(-1/3π, 0) wynika z sumowania wektorów na Rys.8-6b i ich średniej w w czasie T=2π sek, gdy wykonane są 3 obroty płaszczyzny Z. Jego wartość jest ujemna w odróżnieniu od Rys.8-3b, gdzie wektor wykonał  2 “ćwierćobroty” tylko na dodatniej półpłaszczyźnie Z.
Uwaga
W następnych podrozdziałach już nie będzie tak dokładnego opisu trajektorii F(njω0t).
Czytelnik zauważy że:
dla parzystych prędkości obrotowej płaszczyzny Z tj. dla  ω=-4/sek, -6/sek, -8/sek…
parametry scn są zerowe, czyli nie ma harmonicznych dla parzystych pulsacji.
dla nieparzystych prędkości obrotowej płaszczyzny Z tj. dla  ω=-5/sek, -7/sek…
-parametry scn są niezerowe i zmniejszają się do zera gdy ω=-∞. Innymi słowy, amplitudy harmonicznych zmniejszają się do zera, gdy częstotliwość rośnie do nieskończoności.

Rozdział 8.5.2 Trzecia harmoniczna na tle fali prostokątnej parzystej czyli c0+h3(t).
Wg Rys. 8-1c
c3 jest amplitudą zespoloną trzeciej harmonicznej
c3=2*sc3=(-2/3π,0) czyli a3=-2/3π i b3=0
Wg Rys. 8-1e
h3(t)=-(2/3π)*cos(3t)≈-0.212cos(3t)

Rys.8-7
c0+h3(t)=0.5-(2/3π)*cos(3t)+0.5
Czyli trzecia harmoniczna  ze składową stałą c0 na tle fali prostokątnej.

Rozdział 8.5.3 Trzecie przybliżenie fali prostokątnej parzystej czyli S3(t)=c0+h1(t)+h3(t). 

Rys.8-8
S3(t)=c0+h1(t)+h3(t)
Trzecie przybliżenie jest bardziej podobne do fali prostokątnej niż pierwsze z Rys.8-4
A co z drugim? Czyli z S2(t)=c0+h1(t)+h2(t)?  Jest takie samo jak pierwsze tj. S1(t)=c0+h1(t) bo h2(t)=0 i pomijamy go. Podobnie jest z przybliżeniem czwartym, szóstym…, bo h4(t)=h6(t)=…=0.

Rozdział 8.6 Czwarta harmoniczna symetrycznej fali prostokątnej parzystej, a właściwie jej brak bo c4=0 –>h4(t)=a4*cos(4t)=0.
Rozdział 8.6.1 Trajektoria F(njω0t) fali prostokątnej parzystej dla n=4 i ω0=1/sek, czyli F(4j1t).
Płaszczyzna Z obraca się z prędkością ω=-4/sek

Rys.8-9
Trajektoria F(4j1t) fali prostokątnej parzystej
Rys.8-9a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-4/sek wokół punktu (0,0) i wykona 4 obroty w czasie T=2π sek.
Rys.8-9b
Trajektoria F(4j1t)=f(t)*exp(-4j1t) jako  wirujący wektor modulowany funkcją f(t).  Wykona 2 obroty w okresie T=2π sek z przerwą 1π sek pomiędzy. Parametr sc4=0 jako średnia wartość dla T=2π sek  jest oczywisty.
Rys.8-9c
Trajektoria F(4j1t) jako okrąg rysowany przez koniec wektora z Rys.8-9b.
sc4=0
Wniosek
sc4=0 i dlatego harmoniczna dla ω=4/sek nie istnieje.

Rozdział 8.7 Piąta harmoniczna symetrycznej fali prostokątnej parzystej h5(t) =a5*cos(5t).
Rozdział 8.7.1 Trajektoria F(njω0t) fali prostokątnej parzystej dla n=5 i ω0=1/sek, czyli F(5j1t).
Płaszczyzna Z obraca się z prędkością ω=-5/sek

Rys.8-10
Trajektoria F(5j1t) fali prostokątnej parzystej
Rys.8-10a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-5/sek wokół punktu (0,0) i wykona 5 obrotów w czasie T=2π sek.
Rys.8-10b
Trajektoria F(5j1t)=f(t)*exp(-5j1t) jako  wirujący wektor modulowany funkcją f(t).
 W czasie T=2π sek promień R=1 dłużej przebywa na prawej półpłaszczyźnie.   Dlatego jego średnią wartością jako wektor będzie sc5=(1/5π, 0).
Rys.8-10c
Trajektoria F(5j1t) jako okrąg rysowany przez koniec wektora z Rys.8-10b.
Zwróć uwagę na pojawiający się napis “5/4 obrotu”. To powinno przekonać Cię, że trajektoria F(5j1t) dłużej przebywa na prawej półpłaszczyźnie Z. Inaczej-ta część trajektorii jest “cięższa”.

Rozdział 8.7.2 Piąta harmoniczna na tle fali prostokątnej parzystej czyli c0+h5(t).
Wg Rys. 8-1c
c5 jest amplitudą zespoloną piątej harmonicznej
c5=2*sc5=(2/5π,0) czyli a5=2/5π i b5=0   
Wg Rys. 8-1e
h5(t)=(2/5π)*cos(5t)≈0.127cos(5t)

Rys. 8-11
c0+h5(t)=0.5+(2/5π)*cos(3t)
Czyli piąta harmoniczna  ze składową stałą c0 na tle fali prostokątnej.

Rozdział 8.7.3 Piąte przybliżenie fali prostokątnej parzystej czyli S5=c0+h1(t)+h3(t)+h5(t).

Rys.8-12
S5(t)=c0+h1(t)+h3(t)+h5(t)
Piąte przybliżenie jest bardziej podobne do fali prostokątnej niż trzecie z Rys.8-8

Rozdział 8.8 Szósta harmoniczna symetrycznej fali prostokątnej parzystej, a właściwie jej brak bo c6=0 –>h6(t)=b6*cos(6t)=0.
Rozdział 8.8.1 Trajektoria F(njω0t) fali prostokątnej parzystej dla n=6 i ω0=1/sek, czyli F(6j1t).

Rys.8-13
Trajektoria F(6j1t) fali prostokątnej parzystej
Rys.8-13a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-6/sek wokół punktu (0,0) i wykona 6 obroty w czasie T=2π sek.
Rys.8-13b
Trajektoria F(6j1t)=f(t)*exp(-6j1t) jako  wirujący wektor modulowany funkcją f(t).  Wykona 2×1.5 obrotów w okresie T=2π sek z przerwą 1π sek pomiędzy.
Rys.8-13c
Trajektoria F(6j1t) jako okrąg rysowany przez koniec wektora z Rys.8-13b.
sc6=0
Wniosek
sc6=0 i dlatego harmoniczna dla ω=6/sek nie istnieje.

Rozdział 8.9 Siódma  harmoniczna fali prostokątnej parzystej h7(t) =a7*cos(7t).
Rozdział 8.9.1 Trajektoria F(njω0t) fali prostokątnej parzystej dla n=7 i ω0=1/sek, czyli F(7j1t).
Płaszczyzna Z obraca się z prędkością ω=-7/sek

Rys.8-14
Trajektoria F(5j1t) fali prostokątnej parzystej
Rys.8-14a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-7/sek wokół punktu (0,0) i wykona 7 obrotów w czasie T=2π sek.
Rys.8-14b
Trajektoria F(7j1t)=f(t)*exp(-7j1t) jako  wirujący wektor modulowany funkcją f(t).
 W czasie T=2π sek promień R=1 dłużej przebywa na lewej półpłaszczyźnie.   Dlatego jego średnią wartością będzie sc7=(-1/7π, 0).
Rys.8-14c
Trajektoria F(7j1t) jako okrąg rysowany przez koniec wektora z Rys.8-17b.
Zwróć uwagę na pojawiający się napis “1i3/4 obrotu”. To powinno przekonać Cię, że trajektoria F(7j1t) dłużej przebywa na lewej półpłaszczyźnie Z. Inaczej-ta część trajektorii jest “cięższa”.

Rozdział 8.9.2 Siódma harmoniczna na tle fali prostokątnej parzystej czyli c0+h7(t).
Wg Rys. 8-1c
c3 jest amplitudą zespoloną trzeciej harmonicznej
c7=2*sc7=(-2/7π,0) czyli a7=-2/7π i b7=0
Wg Rys. 8-1e
h7(t)=-(2/7π)*cos(7t)≈-0.091cos(7t)

Rys. 8-15
h7(t)+0.5 czyli siódma harmoniczna  ze składową stałą c0 na tle fali prostokątnej.

Rozdział 8.9.3 Siódme przybliżenie fali prostokątnej parzystej czyli S7=c0+h1(t)+h3(t)+h5(t)+h7(t).

Rys.8-16
S7(t)=c0+h1(t)+h3(t)+h5(t)+h7(t)
Siódme przybliżenie jest bardziej podobne do fali prostokątnej niż piąte z Rys.8-12

Rozdział 8.10 Ósma harmoniczna fali prostokątnej parzystej, a właściwie jej brak bo c8=0 –>h8(t)=b8*cos(8t)=0.
Rozdział 8.10.1 Trajektoria F(njω0t) fali prostokątnej parzystej dla n=8 i ω0=1/sek, czyli F(8j1t).

Rys.8-17
Trajektoria F(8j1t) fali prostokątnej parzystej
Rys.8-17a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-8/sek wokół punktu (0,0) i wykona 8 obroty w czasie T=2π sek.
Rys.8-17b
Trajektoria F(8j1t)=f(t)*exp(-8j1t) jako  wirujący wektor modulowany funkcją f(t).  Wykona 4 obroty w okresie T=2π sek z przerwą 1π sek pomiędzy.
Rys.8-17c
Trajektoria F(8j1t) jako okrąg rysowany przez koniec wektora z Rys.8-17b.
sc8=0
Wniosek
sc8=0 i dlatego harmoniczna dla ω=8/sek nie istnieje.

Rozdział 8.11 Pozostałe harmoniczne fali prostokątnej parzystej czyli dla n=9,10,11…∞
Zauważyliśmy, że środki ciężkości scn trajektorii zbliżają się do scn=(0,0) gdy ω rośnie. W dodatku scn harmonicznych parzystych są zerowe. Oznacza to, że harmoniczne maleją ze wzrostem częstotliwości a dla nieskończenie wielkiej częstotliwości ω amplitudy harmonicznych są zerowe, czyli znikają.
Animacja Rys.8-16 pokazuje, że dla n=7 suma S7(t)=c0+h1(t)+h3(t)+h5(t)+h7(t).
A gdy liczba harmonicznych jest nieskończenie wielka, tzn. n=∞
Wtedy suma tych harmonicznych
S∞(t)=c0+h1(t)+h3(t)+h5(t)+h7(t)+h9(t)+…+h∞(t)
jest idealną falą prostokątną f(t) z Rys. 8-1.