Podstawy automatyki
Rozdz.4 Człon całkujący
Rozdz. 4.1 Wstęp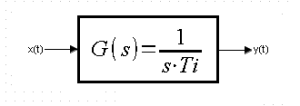
Rys. 4-1
Transmitancja członu całkującego
Dobrze jest, gdy licznik transmitancji ma wartość 1. Wtedy parametr- czas całkowania Ti ma łatwą interpretację–>p.4.4. A gdy nie? Np. G(s)=3/9s? Podziel licznik i mianownik przez 3 a otrzymasz tę samą G(s)=1/3s, tylko w postaci znormalizowanej. Tu widać, że Ti=3sek.
Uwaga dla nieznających całek i pochodnych.
Na razie się nie przejmuj. Wystarczy, że będziesz kojarzył przebieg sygnału wyjściowego y(t) z sygnałem wejściowym x(t) (najczęściej skok jednostkowy) i czasem całkowania Ti. Całkowaniu i różniczkowaniu będą poświęcone rozdziały 11 i 12
Rozdz. 4.2 Schemat z suwakiem i bargrafem
Jak zwykle opis nowego członu dynamicznego zaczynamy od suwaka i bargrafu. Reakcja na wymuszenie suwaka jest bardziej obrazowa niż matematyka
Rys. 4-2
Wciśnij „start”.
Sygnałem wejściowym x(t) jest suwak i miernik cyfrowy
Sygnałem wyjściowym y(t) jest bargraf i miernik cyfrowy
Typową cechą członu całkującego jest prędkość sygnału wyjściowego y(t) która jest proporcjonalna do sygnału wejściowego x(t).
Przekonasz się że:
-zwiększony dodatni sygnał x(t) powoduje szybki wzrost y(t)
-zwiększony ujemny sygnał y(t) powoduje szybki spadek y(t)
–zerowy sygnał x(t) zatrzymuje y(t)
Uwaga:
Miałem problem z ustawienie x(t)=0, dlatego na mierniku widzisz “prawie x(t)=0″. Dlatego jest wtedy “prawie stop”
Co Ci to przypomina? Masz takie urządzenie w domu.
To pilot TV. Raz podajesz wartość „plus” –>głośność rośnie. Podasz „zero”–> głośność stała. Podasz „minus”–>głośność maleje.
Rozdz. 4.3 Schemat z suwakiem i oscyloskopem
A teraz też wejście x(t) z suwaka ale wyjście y(t) z oscyloskopu.
Rys. 4-3
Zmieniałem sygnał x(t) suwakiem. Widoczne jest to na mierniku x(t) i wykresie x(t). Z wykresu czasowego wyraźnie wynika, że prędkość zmian wyjścia y(t) jest proporcjonalna do wejścia x(t). Np. gdy x(t) wzrosło dwukrotnie w okolicach 13 sekundy, to prędkość sygnału y(t) też wzrosła dwukrotnie. Także x(t)=0 zatrzymało y(t) na stałym poziomie.
Rozdz. 4.4 Schemat ze skokiem jednostkowym x(t)=0.1 i oscyloskopem
Rozdz. 4.4.1 Ti=1sek
Poprzedni schemat, gdy sygnał wejściowy pochodził z suwaka, umożliwiał wstępną analizę układu całkującego. Dlatego suwak zamienimy na dokładniejszy generator skoku jednostkowego. Ściślej będzie będzie to skok x(t)=0.1
Rys. 4-4
Odpowiedź członu całkującego o Ti=1 sek. na skok o amplitudzie 0.1
Po czasie t=Ti=1 sek. sygnał wyjściowy y(t) zrównał się z wejściowym x(t).
Powtórzmy doświadczenie dla Ti=2 sek.
Rozdz. 4.4.2 Ti=2sek
Rys. 4-5
Zgodnie z oczekiwaniem sygnał będzie rósł 2 razy wolniej. Zrównanie nastąpiło po czasie t=Ti=2 sek. Teraz możemy zdefiniować czas całkowania Ti dla członu całkującego z Rys. 1-1. Jest to czas Ti, po którym wyjście y(t) zrówna się z wejściem x(t) typu skok.
Rozdz. 4.5 Schemat “ze schodkami” i oscyloskopem
Rozdz. 4.5.1 “2 schodki” i oscyloskopem
Rys. 4-6
Odpowiedź na x(t) “2 schodki”
Gdy sygnał wejściowy wzrósł 2-krotnie to prędkość sygnału wyjściowego też wzrosła 2-krotnie.
Rozdz. 4.5.1 “4 schodki” i oscyloskop
Rys. 4-7
Odpowiedź na x(t) “4 schodki”
Przy każdym schodku prędkość wzrasta 2-krotnie
Rozdz. 4.6 Schemat z sygnałem narastającym liniowo i oscyloskopem
Nieprzypadkowo poprzednie sygnały wejściowe x(t) były schodkowe. Dlaczego? Bo narastający liniowo sygnał możemy traktować jako z nieskończoną ilością schodków.
Rys. 4-8
Gdy sygnał wejściowy narasta liniowo x(t)=t to y(t) rośnie jak funkcja kwadratowa. Sprawdź, podstawiając różne wartości pod t.
Człon całkujący jak sama nazwa wskazuje całkuje sygnał wejściowy x(t) dając na wyjściu parabolę y(t).
Z drugiej strony analiza matematyczna mówi że całka oznaczona z funkcji x(t)=t też jest parabolą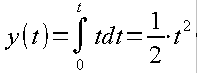
Rys. 4-9
Sprawdź, że np. dla t=4 x(t)=5, y(t)=12.5
Rzeczywiście, podstaw t=5 to się przekonasz. Czyli teoria zgadza się z praktyką. Jeżeli nie znasz analizy matematycznej, to się nie przejmuj. Na razie potraktuj, że całką oznaczoną od 0 do t z x(t) jest sygnał y(t) członu całkującego 1/s .
Rozdz. 4.7 Schemat ze skokiem dodatnim i ujemnym i oscyloskopem
Jest to doskonalsza wersja doświadczenia z Rys. 4-3, w którym sygnał x(t) podawany jest z generatora, czyli bardziej precyzyjnego urządzenia niż suwak.
Rys. 4-10
W podobny sposób regulujesz pilotem głośność w TV, ale tu możesz jeszcze sterować szybkością przesuwania paska. Może to być też siłownik jako silnik prądu stałego z przekładnią. Wejście to napięcie a wyjście to położenie dźwigni siłownika.
Rozdz. 4.8 Schemat z impulsem Diraca i oscyloskopem
Rys. 4-11
W przyrodzie nie ma idealnego impulsu Diraca. Jest tylko jego przybliżenie.
Tu impuls prostokątny o amplitudzie 100 i czasie trwania 0.01 sek.
Rozdz. 4.9 Typowe człony całkujące.
Kondensator.
Wejście – prąd ładujący kondensator
Wyjście – napięcie na kondensatorze
Gdy kondensator jest ładowany stałym prądem, to napięcie narasta liniowo, tym szybciej im mniejsza jest pojemność C kondensatora
Wanna zatkana korkiem.
Zakładam, że wanna to prostopadłościan.
Wejście – przepływ wody z kranu, pośrednio stopień otwarcia kranu
Wyjście – poziom wody
Jeżeli przepływ jest stały, to poziom będzie narastał liniowo. Tym szybciej im mniejsza jest powierzchnia wanny.
Siłownik elektryczny.
Zakładam że mamy idealny silnik prądu stałego z przekładnią.
Wejście – napięcie na silniku
Wyjście – kąt położenie wału siłownika
Stałe napięcie na silniku spowoduje liniowy przyrost kąta. Prędkość przyrostu jest proporcjonalna do napięcia
