Podstawy automatyki

Rozdz. 22 Regulacja ciągła

Rozdz. 22.1 Wstęp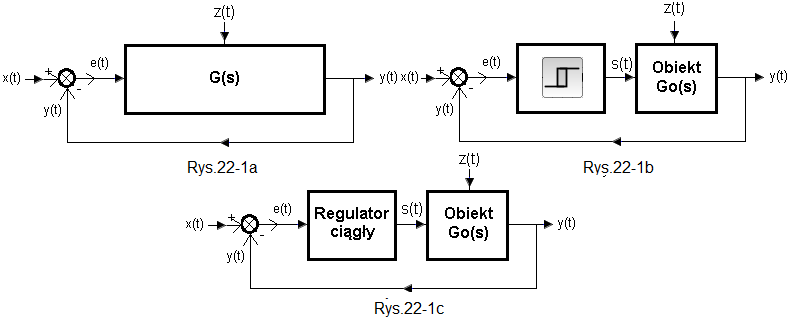

Rys. 22-1
Rys. 22-1a
Najbardziej ogólny schemat regulacji pokazujący:
– wartość zadaną x(t)
– sygnał wyjściowy y(t) – inna nazwa zmienna procesowa pv(t)
– zakłócenie z(t)
– uchyb regulacji e(t)
Rys. 22-1b
Dokładniejsza wersja w której cały obiekt został podzielony na regulator dwupołożeniowy i właściwy obiekt Go(s).
Za regulatorem pojawił się sygnał sterujący s(t).
Rys. 22-1c
Zamiast regulatora dwupołożeniowego jest regulator ciągły typu P, PI, PD lub PID.
Sygnał sterujący s(t) w odróżnieniu od regulatora dwupołożeniowego jest w stanie ustalonym stały.

Rozdz. 22.2 Postać ogólna i typowa obiektu sterowania Go(s)
Od tej pory interesuje nas tylko regulacja ciągła czyli Rys. 22-1c. Ale najpierw zajmiemy się samym obiektem którym będzie sterował regulator. Obiekt to transmitancja Go(s) o postaci: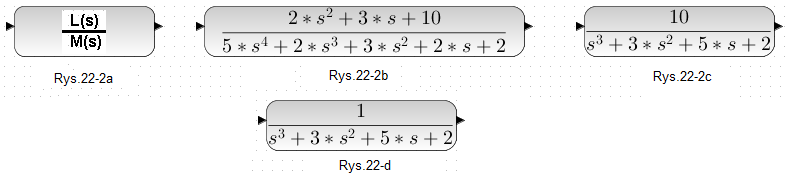

Rys. 22-2
Rys. 22-2a 
Ogólna postać transmitancji gdzie licznik L(s) i mianownik M(s) to wielomiany któregoś tam stopnia.
Rys. 22-2b 
Konkretny przykład gdzie licznik L(s) jest wielomianem stopnia 2 a mianownik M(s) stopnia 4.
Rys. 22-2c 
Przypadki transmitancji obiektowych Go(s), gdy L(s) jest stopnia większego od 1 są raczej rzadkie! Typowym licznikiem L(s) jest tylko wzmocnienie K. Tu K=10
Rys. 22-2d 
Z kolei najczęściej K=1 i taką transmitancją będziemy dalej traktować jako typową. Mianownik M(s) jest w dalszym ciągu wielomianem dowolnego stopnia n. Często M(s) jest iloczynem.. Np M(s)=(1+sT1)*(1+sT2)*(1+sT3)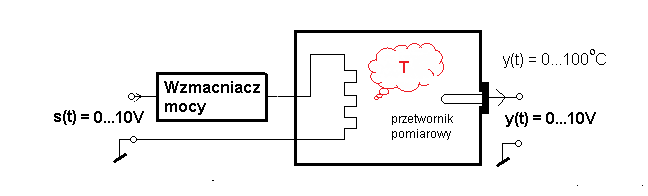

Rys. 22-3
Przykład na to, że typowe jest K=1 jak na Rys. 22-2d
Obiektem jest zbiornik wody z grzałką oporową sterowaną przez wzmacniacz mocy. Temperatura wody będzie sterowana w zakresie np. 0…+100ºC. Mierzymy ją termometrem oporowym Pt100 o zakresie pomiarowym 0…+100ºC–>napięcie 0…+10V. Termometr składa się z drucika platynowego w metalowej obudowie-rurce i przetwornika ΔR–>0…10V. ΔR jest przyrostem rezystancji R spowodowanym wzrostem temperatury. Rurka z drucikiem jest dość delikatna i dlatego umieszczona jest jeszcze w pochwie metalowej. Przetwornik wystaje na zewnątrz zbiornika, skąd sygnał może być doprowadzony kabelkiem do regulatora. Na rysunku widać jak pochwa przez otwór wchodzi do zbiornika.
Wzmacniacz mocy jest tak dostrojony, że +10V na wejściu podgrzeje po pewnym czasie wodę do +100ºC, ale bez wrzenia! Wtedy też przetwornik temperatury da +10V. A gdy nie uda się osiągnąć tej wartości, tylko np +55ºC. Tzn. że musisz dobrać grzałkę o większej mocy i ewentualnie zwiększyć moc wzmacniacza.
Czy widzisz, że całość, tzn. relację między s(t) a y(t) możesz traktować jak wzmacniacz o wzmocnieniu Ko=1? Oczywiście z pewnymi stałymi czasowymi T które są zawarte w mianowniku transmitancji Go(s). Stopień wielomianu M(s) jest tym większy, im dokładniej znamy opis matematyczny procesu ogrzewania wody w zbiorniku. Pierwszym, najmniej dokładnym przybliżeniem, będzie człon inercyjny o jednej stałej czasowej T.
Podsumowując
Obiekt Go(s) to zbiornik z wodą + grzałka + wzmacniacz mocy. Wzmocnienie samego obiektu Ko=1. A gdy przed obiektem, czyli przed wzmacniaczem mocy jest jeszcze zwykły wzmacniacz napięcia ( nie mocy!) o wzmocnieniu np. Kp=5? Później się dowiesz, że tym wzmacniaczem jest regulator proporcjonalny albo inaczej regulator P. Wtedy wzmocnienie całego toru otwartego to K=Kp*Ko=Kp, bo Ko=1 Czyli zależy tylko od nastawy regulatora P -wzmocnienia Kp. A to ułatwi nam tzw. strojenie regulatora. Czyli znalezienie takiego Kp, które zapewni optymalną odpowiedź na skok x(t).

Rozdz. 22.3 Podział obiektów Go(s) na statyczne i astatyczne
Automatyk zaczyna projekt od dobrego poznania obiektu G(s) którym ma sterować, czyli jego własności statycznych i dynamicznych.
A te dzielą się na:
-statyczne
-astatyczne
Rozdz. 22.3.1 Obiekty G(s) statyczne
Badasz jednoczesną odpowiedź na skok x(t) trzech typowych obiektów statycznych

Rys. 22-4
G1(s)-Inercyjny K=1 T=2sek
G2(s)-Dwunercyjny K=1, T1=2sek, T2=3sek
G3(s)-Oscylacyjny K=1, q=0.3, T=1sek –>rozdz.7 Rys.7.2
W stanie ustalonym wszystkie wyjścia w odpowiedzi na skok x(t) są stałe, czyli statyczne. Stąd nazwa obiekty statyczne. Zauważ, że każdy mianownik M(s) transmitancji G(s) nie ma pierwiastka zerowego.
Rozdz. 22.3.2 Obiekty Go(s) astatyczne
Jednoczesna odpowiedź na skok x(t) trzech typowych obiektów astatycznych.
W mianowniku M(s) występują pierwiastki zerowe. Nawet podwójne–>G2(s).

Rys. 22-5
G1(s)-Całkujący 
G2(s)-Podwójnie Całkujący 
G3(s)-Całkujący z inercją
W stanie ustalonym wyjścia y(t) cały czas rosną! y1(t), y3(t) ze stałą prędkością. Dla y2(t) jeszcze lepiej, z prędkością która cały narasta – jak po starcie rakiety Apollo! Jest to typowe dla obiektów astatycznych, czyli po polsku niestatycznych. Czyli takich, które w odpowiedzi na skok x(t) w stanie ustalonym poruszają się ze stałą lub z zwiększająca się prędkością. Cechą charakterystyczną tych obiektów jest też niezerowe wyjście przy zerowym wejściu w stanie ustalonym. Ta cecha zapewnia właśnie zerowy zerowy uchyb regulacji i jest związana ze składową I regulatora PID. Będzie o tym mowa później.
Interpretacja
G1(s) – idealny silnik prądu stałego z przekładnią i wajchą. Czyli po naszemu siłownik. Wejście to napięcie na silniku, wyjście to kąt α. To α może sterować np. zaworem na rurociągu. Podkreślam, nie ma tu ujemnego sprzężenia zwrotnego, czyli kąt może się zmieniać teoretycznie od – do + nieskończoności. W praktyce silnik będzie wcześniej wyłączony przez tzw. krańcówki. A jeszcze wcześniej to wyłączony lub nawet „zawrócony” przez regulator zapewniający ujemne sprzężenie zwrotne.
G3(s) – To samo tylko nieidealny siłownik. Czyli uwzględniający bezwładności i tarcia. Stąd ten efekt rozpędzania, zanim osiągnie stałą prędkość
G2(s) – Rakieta jak wyżej, lub siłownik który cały czas zwiększa prędkość!
Ten ostatni to przypadek czysto teoretyczny, raczej nie stosowany w praktyce. A może są takowe?
Obiekt astatyczny można zatrzymać jedynie przez podanie zera na wejście.
Jeszcze bardziej trywializując.
Przy niezerowym wejściu x(t):
Statyczny w stanie ustalonym nie rusza się. Astatyczny w stanie ustalonym rusza się.

Rozdz. 22.4 Porównanie obiektów statycznych i astatycznych ze względu na stabilność
Rozdz. 22.4.1 Wstęp
Chyba łatwiej jest sterować czymś, co wstanie ustalonym się nie rusza, niż tym co się rusza.
Dlatego obiekty statyczne są „łatwiejsze” niż astatyczne. Sprawdźmy to.
Rozdz. 22.4.2 Statyczne
Typowy obiekt statyczny 2 stopnia z ujemnym sprzężeniem zwrotnym.

Rys. 22-6
Układ doszedł do stanu ustalonego y=0.91. Właśnie uchyb ustalony, tu e=0.09, tym mniejszy im większe wzmocnienie K, jest typowy dla układów statycznych z ujemnym sprzężeniem zwrotnym. Chcąc zmniejszyć uchyb, należy zwiększyć K. Spowoduje to jednak większą oscylacyjność a czasem nawet niestabilność. Można udowodnić np. z kryterium Nyquista, że układy typu dwuinercyjnego, nie wejdą nigdy w niestabilność, nawet przy dużym K. Dlatego, że ich charakterystyki amplitudowo-fazowe przechodzą tylko przez 2 ćwiartki. Mogą wejść w niestabilność tylko te transmitancje, których mianownik M(s) jest większego stopnia niż 2.
Rozdz. 22.4.3 Astatyczne
Astatyczne są trudniejsze do sterowania, bo po zamknięciu ujemnym sprzężeniem zwrotnym łatwiej stają się niestabilne.

Rys. 22-7
Pojawił się zerowy pierwiastek s=0 w mianowniku M(s) transmitancji. Typowa cecha układów astatycznych. Dajmy w 5 sek na wejście „prztyka” x(t). Ja już wiem co się wydarzy. Dlatego radykalnie zmieniłem skalę oscyloskopu. Poprzednio było 0…+1.2, teraz -150…+150. Nieszczęście. Niestabilność, drgania od – do + nieskończoności. I zrobiła to tylko mała literka s w transmitancji na Rys. 22-7.
A jak uczynić układ stabilnym? Generalnie to robi się różne rzeczy. Pierwsza myśl to zmniejszenie K.
Będzie to dość radykalne zmniejszenie z K=10 na K=0.25.

Rys. 22-8
Najważniejsze, że odpowiedź jest stabilna. Ale jak wolno! Porównaj z Rys. 22-6, gdzie stan ustalony wystąpił po ok. 10 sek., tu po 55 sek. Ale za to jest jedna fajna rzecz. Po 45 sek. mamy stan y(t)=x(t). Czyli uchyb zerowy! I to niezależnie od K! Dla np. K=0.1 uchyb ustalony też byłby zerowy. Niestety kosztem jeszcze większej wołowatości.
Czyli obiekty astatyczne objęte ujemnym sprzężeniem zwrotnym są bardziej podatne na oscylacje i niestabilność. Wolniej też dochodzą do stanu ustalonego. Za to mogą sprowadzić uchyb do zera, co jest oczywiście ich główną zaletą.
Rozdz. 22.4.4 Porównanie statycznych i astatycznych ze sprzężeniem zwrotnym na wspólnym wykresie
Porównamy odpowiedzi z:
-Rys. 22-6 (statyczny stabilny)
-Rys. 22-7 (astatyczny niestabilny)
-Rys. 27-8 (astatyczny stabilny).
Na tych rysunkach były różne nastawy oscyloskopu dla czasu t  i y(t). Dlatego zbadamy ponownie wszystkie  3 transmitancje, ale tym razem jednocześnie. Coś w rodzaju sprowadzania do wspólnego mianownika.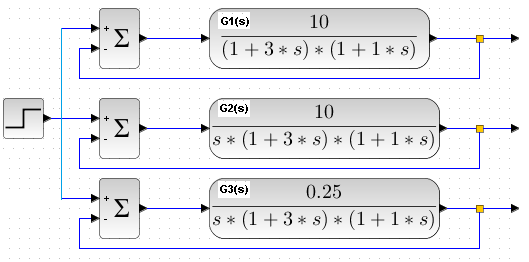

Rys. 22-9
Wciśnij „start”
Ten sam skok x(t) wchodzi na wszystkie na 3 obiekty:
– G1(s) statyczny
– G2(s) astatyczny – duże wzmocnienie K=10 dlatego niestabilny
– G3(s) astatyczny – małe wzmocnienie K=0.25 dlatego stabilny

Rys. 22-10
Te pionowe żółte kreski to narastające drgania obiektu G2(s) z ujemnym sprzężeniem zwrotnym. Na Rys. 22-7 była odpowiedź na x(t)=”prztyk”  a teraz x(t)=skok. Były też inne  nastawy oscyloskopu. Nie widać oczywiście drgań po „stronie ujemnej” wykresu.
Wnioski:
– Układy astatyczne są bardziej podatne na niestabilność niż statyczne
– Układ stabilny statyczny G1(s) wyraźnie szybciej dochodzi do stanu ustalonego, niż stabilny astatyczny G3(s)
– Układ stabilny astatyczny G1(s) może mieć uchyb zerowy! Oczywiście pod warunkiem, że jest stabilny, co jest trudniejsze dla astatycznych. Właśnie ten zerowy uchyb regulacji e(t) w stanie ustalonym jest podstawową zaletą astatyzmu.
Układy statyczne w odróżnieniu od astatycznych zapewniają zerowy uchyb tylko dla wzmocnienia K=nieskończoność. Ten teoretyczny raczej warunek może spowodować duże oscylacje, a nawet niestabilność.

Rozdz. 22.5 Człowiek jako regulator ciągły
Rozdz. 22.5.1 Wstęp
Zgłosił się do nas Klient w sprawie projektu układu regulacji dla obiektu z Rys. 22-3.
Jest to biedny Inwestor i nie stać go na regulator. Sam będzie za niego robił, czyli będzie sterował ręcznie
O samym obiekcie powiedział tylko:
– jest to zbiornik z cieczą z , która w ogóle nie zmienia stanu skupienia. To założenie ułatwi nam analizę.
– chce regulować w sposób ciągły temperaturę w zakresie 0ºC…+50ºC
Zależy mu też na jak najszybszym przejściu z jednego stanu do drugiego np. z +20ºC na +40ºC lub odwrotnie z +40ºC na +20ºC. To ostatnie wiąże się z aktywnym chłodzeniem, czyli grzałka zamieni się w lodówkę! Stąd ten chłodzący element Peltiera.
A dlaczego regulator ma być ciągły a nie dwupołożeniowy? Bo wie, że w stanie ustalonym dla regulacji dwupołożeniowej sygnał wyjściowy y(t) cały czas oscyluje wokół pewnej wartości średniej. Po prostu taką urodę ma ten typ regulacji. A to bardzo źle wpływa na jakość produktu Klienta!
Rozdz. 22.5.2 Człowiek jako regulator ciągły bez sprzężenia zwrotnego
Zaproponowaliśmy sterowanie w układzie otwartym, lub jak kto woli sterowanie bez sprzężenia zwrotnego.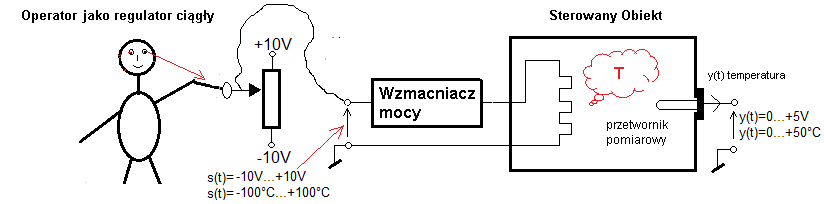

Rys. 22-11
Jest to prawie powtórzony Rys. 22-3 z człowiekiem jako regulatorem i potencjometrem jako bezpośrednim urządzeniem sterującym. O samym obiekcie wiemy już, że zmianom napięcia s(t)=0…+10V na jego wejściu odpowiadają takie same zmiany y(t)=0…+10V na wyjściu, ale w stanie ustalonym! Ściślej takie same zmiany ale tylko dla s(t)=0…+5V. Potem dla  s(t)=+5V…+10V  wyjście y(t)=+5. Termometr stoi w miejscu.  Po prostu założyliśmy, że temperatura na wyjściu nigdy nie przekroczy +50ºC i nie ma sensu dawać termometru 0… +100ºC.
Czyli cały skomplikowany obiekt z grzałką, cieczą i termometrem został zredukowany, wręcz zdegradowany do zwykłego wzmacniacza o wzmocnieniu K=1 z pewnymi stałymi czasowymi. Bo gdy na potencjometrze będzie np. +3V to na wyjściu w stanie ustalonym  termometru też będzie +3V! Takie podejście bardzo ułatwia dobór regulatora ciągłego, w domyśle PID, w którym cała dynamika układu zamkniętego będzie zależała tylko od nastaw Kp, Ti i Td tego regulatora. Będzie o tym mowa w następnych rozdziałach.
Instrukcja Obsługi
Klienta trzeba nauczyć sterowania.
1. Sterować będzie potencjometrem zapewniającym napięcie w zakresie -10V…+10V. Ma on 200 mm długości i jest wyskalowany w jednostkach 0.1V<=>1ºC  albo 0.1mm<=>1ºC. W środku jest 0ºC, na górze +100ºC a na dole -100ºC.
Jeszcze jedno Jest to kurs automatyki a nie fizyki. Dlatego ciecz nie zmienia stanu skupienia–>nie zamarza ani nie paruje.
Poza tym nasza elektryczna grzałka grzeje przy napięciach dodatnich i chłodzi przy ujemnych!
Jest takie dziwadło znane już od XIX wieku – element Peltiera.
Klient czyta instrukcję z mieszanymi uczuciami
Ma do dyspozycji:
-urządzenie sterujące–> potencjometr o zakresie  -10V…+10V, inaczej -100ºC…+100ºC
-przetwornik temperatury o zakresie 0…+50ºC, inaczej 0…+5V
Klient dziwi się. Mam sterować temperaturą cieczy w zakresie 0…+50ºC?
Po co nadmiarowa „grzejąco/chłodząca” moc np. -10 kW…+10kW, skoro dla 0ºC…+50ºC wystarczy 0…+5 kW?
A może projektant chce mnie wpuścić w koszta, jak taksówkarz jadący nie najkrótszą trasą?
Po co mi sterowanie umożliwiające osiągnięcie temperatur -100ºC…+100ºC a zakres przetwornika temperatury to tylko 0…+50ºC?
I tak z wątpliwościami przystąpił do pierwszej próby podgrzania cieczy do +50ºC.
Pierwsza próba podgrzania cieczy do +50ºC.
Podchodzi do problemu ostrożnie jak pies do jeża. Dlatego przesunął w górę o 50 mm suwak na s(t)=+5V lub jak kto woli na +50ºC i czeka na efekt.
Klient ślepo wierzy w sterujący suwak s(t) i nawet nie patrzy miernik przetwornika! Dodam jeszcze, że temperatura otoczenia to 0ºC. Wiara klienta miała podstawy. Po pewnym czasie temperatura wzrosła do +50ºC jak poniżej.

Rys. 22-12
Widzisz w górnym lewym rogu jak operator przesunął po ok. 5sek suwak potencjometru z 0V na +3V co odpowiada “skokowi” temperatury z 0ºC na +30ºC. Skok nie był idealny. Nasz klient ma swoje lata i łapka drży trochę. Tak czy owak widzisz jak pięknie temperatura y(t) dochodzi z 0ºC na +30ºC.
Był to przykład sterowania w układzie absolutnie otwartym. Tzn. Klient nawet nie spojrzał na termometr, tylko całkowicie ufał suwakowi sterującemu. Sygnał wyjściowy y(t) nie miał żadnego wpływu na sygnał  sterujący s(t) z suwaka! A sam przebieg to klasyczny człon inercyjny K=1 i T=10sek 
Rozdz. 22.5.3 Człowiek jako regulator ciągły ze sprzężeniem zwrotnym!
Zdawałoby się, że sterowanie w układzie otwartym jest super! Klient ustawił suwak na s(t)=+3V=+30mm=+30ºC i po pewnym czasie temperatura doszła do +30ºC Czego chcieć więcej?
Ale
Po pierwsze primo
Temperaturą otoczenia było 0ºC. Gdyby było inaczej np. +13ºC to w stanie ustalonym byłoby y(t)=+43ºC (w rzeczywistości trochę mniej), a nie y(t)=+30ºC!
Po drugie primo
Zakładaliśmy, że obiekt został absolutnie rozpracowany matematycznie i fizycznie. Tzn. wiemy, że przy temperaturze otoczenia 0ºC i s(t)=+3V na potencjometrze, temperatura cieczy powinna ustalić się dokładnie na y(t)=+30ºC.
Po trzecie primo
Zakładaliśmy, że potencjometr jest idealny. Tzn. że 30 mm w górę to dokładnie s(t)=+3V
Po czwarte itd…
Krótko mówiąc zakładaliśmy, że wszystko jest idealne. A to były tylko błogie życzenia. Nie możemy być więc pewni, że 30 mm w górę na potencjometrze podgrzeje ciecz dokładnie na +30ºC. Wniosek może być tylko jeden.
Operator procesu musi cały czas obserwować sygnał wyjściowy y(t) i korygować go suwakiem potencjometru.
Czyli schemat powinien wyglądać następująco.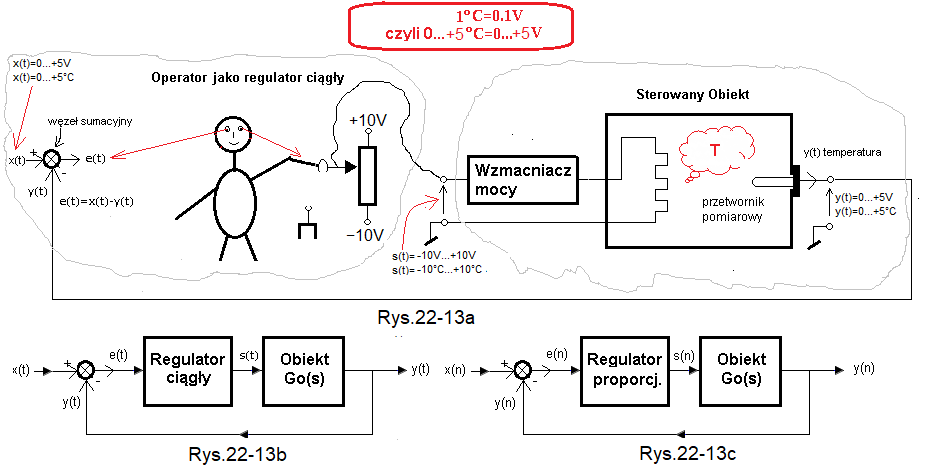

Rys. 22-13
Człowiek jako regulator
Rys. 22-13a
Operator cały czas obserwuje sygnał wyjściowy y(t) i w zależności od sytuacji koryguje go sygnałem napięciowym s(t) z potencjometru. Czyli w „głowie” oblicza uchyb e(t)=x(t)-y(t) i tak kombinuje żeby uchyb e(t) w stanie ustalonym był jak najmniejszy. Ideał niemożliwy do osiągnięcia to to w każdej chwili e(t)=0. Wtedy y(t)=x(t), czyli sygnał wyjściowy y(t)=x(t). Inaczej–> y(t) stara się naśladować wartość zadaną x(t).
Rys. 22-13b
Operator stosował jakiś algorytm do sprowadzania uchybu e(t) do zera.  Może om być wykonany także przez mikroprocesor.
Wtedy człowiek zostaje zastąpiony regulatorem jak na powyższym rysunku.
Rys. 22-13c
Jest wiele takich algorytmów. Jeden z nich jest zaskakująco prosty!
krok 1  oblicz aktualny uchyb regulacji e(t)=x(t)-y(t)
krok 2 oblicz sygnał sterujący s(t)=Kp*e(t)
krok  3 wróć do krok 1
W ten sposób będzie realizowany algorytm regulatora proporcjonalnego P w którym przy skokowej zmianie wartości zadanej x(t)=1 sygnał wyjściowy y(t) będzie dążył do wartości prawie równej wartości zadanej np. y(t)=0.9 gdy Kp=10. Czyli uchyb będzie sprowadzony „prawie” do zera–>e(t)=0.1. Tym dokładniej im większe jest wzmocnienie ustalone regulatora i obiektu Go(s).
Wróć do p. 16.3 z rozdziału 16, to będziesz wiedział dlaczego.
Jeszcze jedno. Sygnał y(t) w praktyce rzadko wychodzi poza zakres 0…+5V czyli 0…+50ºC. Natomiast sygnał sterujący s(t) umożliwia osiągnięcie stanów -10V…+10V! czyli -100ºC…+100ºC!* Po co takie przesterowanie?
Umożliwia szybsze przejście z jednej temperatury do drugiej. Ogólnie z jednego stanu do drugiego. Chociaż sygnały wejściowy x(t) i wyjściowy y(t) zmieniają się tylko w zakresie 0…+5V czyli 0…+50ºC. Takie przesterowania są typowe dla każdej regulacji, w tym PID.
Sprawdźmy jak działa Człowiek-Regulator.
Sam obiekt Go(s) jest zbiornikiem z grzałką o takiej mocy, że w czasie ok 40 sek tj 4*10 sek ciecz osiągnęła temperaturę 100ºC. Będę więc sterował obiektem Go(s) – członem inercyjnym o wzmocnieniu K=1 i stałej czasowej T=10 sek. Ściślej, będę starał się żeby y(t), czyli temperatura cieczy,  była jak najbardziej podobna w czasie do wartości zadanej x(t) czyli  skoku od 0 do +30ºC. Przekonasz się, jak ciężkie jest życie Pana Regulatora. Twoim zadaniem będzie obserwowanie wartości zadanej x(t) i wyjścia y(t) czyli temperatury wody w szklance oraz sterowania s(t) suwakiem potencjometru przez autora. Ruchy suwaka będą widoczne w lewym górnym rogu.

Rys. 22-14
Widać jak w 5 sekundzie człowiek daje sygnał sterujący s(t) na maxa, tzn. ustawia suwak potencjometru na +10V czyli na +100°C. Zauważ, że jest to większy sygnał niż potrzeba tj. +30°C. Ale dzięki temu sygnał y(t) będzie szybciej dochodził do +30°C. Jak się później przekonasz tak początkowo zachowują się regulatory P, PI i PID. Potem widząc jak rośnie y(t) zmniejsza s(t). Bardziej doświadczony operator dałby nawet intensywne chłodzenie po to żeby szybciej dość do y(t)=+30°C.  Przy takim sterowaniu mogą pojawić się nawet malejące oscylacje. Widać to nawet przy “ostrożnym” sterowaniu na Rys. 22-14. W końcu y(t)=s(t) i jest w miarę zbliżone do x(t). A dlaczego nie dokładnie x(t)? No cóż, autor ma swoje lata i nieduży uchyb e(t) potraktował jako zerowy. A tak nie jest.

Rozdz. 22.6 Człowiek-Regulator z zakłóceniami
Rozdz. 22.6.1
Na obiekt Go(s) wody działają zakłócenia
z(t)=+20ºC
z(t)=-20ºC
Zakłóceniem może być np. wymiennik ciepła przez który płynie ciecz ciepła +20ºC lub chłodząca -20ºC opisany na Rys. 21-12 rozdz. 21. Na schematach, zakłócenie z(t) symulowane są dodatnim lub ujemnym skokiem napięcia+/-20ºC.
Rozdz. 22.6.2 Człowiek-Regulator nie reagujący na zakłócenie z(t)=+20°C
Człowiek reaguje tylko na x(t), czyli dokładnie tak jak na Rys. 22-14. W 35 sek pojawi się zakłócenie z=+20°C, na które nie zareaguje!

Rys.22-15
Człowiek nie reaguje na skokowe zakłócenie z(t)=20ºC. Potem tłumaczył się, że był ciekaw jaki będzie jego efekt. No i zobaczył. Temperatura wzrosła do y(t)=+50°C.
Rozdz. 22.6.3 Człowiek-Regulator reagujący na zakłócenie z(t)=+20°C

Rys.22-16
Do 35 sek autor zachowuje się tak na Rys.22-14 i Rys.22-15.  Po 35 sek, gdy pojawia się z(t)=+20°C zadziałał prawidłowo. Tak zmniejszał s(t), aż temperatura znowu wróciła w przybliżeniu do y(t)=+30°C. Brawo.  Zielony uchyb e(t) spadł prawie do 0. A dlaczego “prawie”, a nie “dokładnie” do 0. No cóż, taki wzrok ma autor. Za młodu sterowałby dokładniej.
Rozdz. 22.6.4  Człowiek-Regulator nie reagujący na zakłócenie z(t)=-20°C

Rys. 22-17
Jest to eksperyment podobny do Rys. 22-15. Jedyna różnica. Zamiast dodatkowej grzałki włożona została chłodnica. Jej moc została tak dobrana, że w stanie ustalonym temperatura cieczy  y(t) zbiorniku została obniżona o -20°C.  Człowiek reaguje tylko na x(t)  a nie na zakłócenie z(t)=-20°C. Temperatura cieczy  y(t) rzeczywiście spadła o -20°C.
Rozdz. 22.6.5 Człowiek-Regulator reagujący na zakłócenie z(t)=-20°C

Rys.22-18
Regulacja analogiczna do Rys.22-7 
Zakłóceniem jest tu chłodzenie zamiast grzania. Człowiek prawidłowo zareagował na chłodzenie zwiększając potencjometrem s(t) grzanie.

Rozdz. 22.7 Wnioski
1. W regulacji ciągłej sygnał sterujący s(t) przyjmuje wszystkie wartości s(t) w zakresie Min…Max
2. Automatyk ma do czynienia z 2 typami obiektów dynamicznych Go(s)
-Statyczne–>Rys.22-4
-Astatyczne–>Rys.22-5
3. Zakresy wartości zadanej x(t) i wyjściowej y(t) są takie same. Np. 0ºC…+50ºC (0…+5V). I tak jest, albo powiem asekuracyjnie, tak powinno być w układach sterowania z prawdziwymi regulatorami. Czyli wzmocnienie w stanie ustalonym między wyjściem a wejściem jest (zawsze?)K=1.
4. Sygnał sterujący s(t) powinien mieć większy zakres niż powyższe 0ºC…+50ºC. W naszych przykładach było to -100ºC…+100ºC (-10V…+10V).To poprawia dynamikę! Często ten zakres jest jeszcze większy. A już mniejszy zakres jest niedopuszczalny! Po prostu pewne stany byłyby nieosiągalne. Raczej trudno byłoby zagrzać wannę wody „szklankową” grzałką elektryczną!
5. Chociaż sterowałeś ręcznie, to było jednak ujemne sprzężenie zwrotne. Zamykało się przez Człowieka jako Pana Regulatora. Dlatego przebiegi są (trochę naciągając rzeczywistość) podobne do układów z „prawdziwym” regulatorem typu P, o czym przekonasz się w następnych  rozdziałach.
6. Człowiek-Regulator stara się odpowiednio sterując potencjometrem s(t) aby sygnał wyjściowy y(t) naśladował wartość zadaną x(t). W tym chwalebnym celu próbują przeszkodzić mu sygnały zakłócające z(t). Gdy zakłócenie z(t) grzeje to regulator każe chłodzić i vice versa.