Scilab

Rozdział 14 XCOS-Układy regulacji automatycznej

Rozdz. 14.1 Wstęp
XCOS idealnie nadaje się do analizy Układów regulacji automatycznej.
Najpierw zbadamy najłatwiejszy do zrozumienia Układ regulacji dwupołożeniowej. W nim regulatorem jest przekaźnik z histerezą, którego styki sterują grzałką elektryczną  pieca. Piec będzie starał się utrzymać temperaturę w pewnym stałym zakresie. W pewnej chwili włączy się dodatkowa grzałka. Regulator powinien zmniejszyć dopływ mocy,  tak żeby średnia temperatura pozostała taka sama. W ten sposób poznasz podstawowe pojęcia Teorii Regulacji. Wartość zadaną x(t) i zakłócenie z(t)–>włączenie dodatkowej grzałki. 
Potem zajmiemy się Układem Regulacji P, I, PI i PID. Regulacja PID jest najczęstszym typem regulacji i dla wielu regulacja PID jest po prostu regulacją.

Rozdz. 14.2 Układ Regulacji dwupołożeniowej
Rozdz. 14.2.1 Przekaźnik z histerezą
Jak działa przekaźnik i co to jest histereza, pokaże animacja.
Zwykle zachęcam do samodzielnego zaprogramowanie eksperymentu XCOS-em, ale tu wystarczy tylko analiza animacji.

Rys.14-1
Zasada działania przekaźnika z histerezą.
Typowy przekaźnik załącza np. przy +5V a wyłącza przy np. +4,8V. Bardziej użyteczna w automatyce będzie taka charakterystyka przekaźnika, który załącza się przy pewnych wartościach dodatnich a wyłącza przy ujemnych. Tu załącza dla x(t)=+0.2 a wyłącza gdy x(t)=-0.2. Ten twór musi być wspomagany jakąś prostą elektroniką, w szczegóły której nie będziemy wchodzić.
Sygnał wewnątrz paska -0.2…+0.2 może się zmieniać „wte i we wte” i nie wpływa na sygnał wyjściowy. Może nawet wrócić tam skąd przyszedł i ponownie „bezkarnie” wróć do paska. „Bezkarnie”, czyli bez zmiany stanu przekaźnika.
Rozdz. 14.2.2 Układ regulacji dwupołożeniowej z zakłóceniem dodatnim z(t)=+30°C
Obiektem jest piec jako człon inercyjny o T=15sek.  Przekaźnik włącza taką moc, która spowodowałaby temperaturę y(t)=+100ºC w stanie ustalonym. Przy wyłączeniu temperatura y(t) dąży do temperatury otoczenia tj. 0°C. W 5 sekundzie pojawi się wartość zadana temperatury +50°C, która cały czas będzie stała. Zakłócenie z(t)=+30°C (włączenie dodatkowej grzałki) wystąpi w 35 sek. Czy dodatnie zakłócenie zostanie skompensowane średnim spadkiem mocy na grzałce?

Rys. 14-2
W 35 sekundzie wystąpiło zakłócenie z(t)=+30°C.
Dalsza analiza jest podobna jak bez zakłóceń tylko:
– przy włączeniu temperatura szybko dąży do +130°C=100°C+30°C (bo włączyła się dodatkowa grzałka)
– przy wyłączeniu temperatura wolno dąży do +30°C (a nie do temperatury otoczenia, bo działa dodatkowa grzałka)
Są więc krótkie włączenia i długie wyłączenia grzałki. Średnia moc dostarczona do pieca została więc zmniejszona. Tak czy owak histereza przekaźnika trzyma temperaturę w tym samym pasie -5°C…-+5°C co przed zakłóceniem.
Spróbuj samemu narysować schemat w XCOSie i nacisnąć “Start”. Blok HYSTERESIS znajdziesz w palecie Nieciągłości. Pozostałe bloki znasz i wiesz gdzie szukać. Dasz radę.

Rozdz. 14.3 Układ regulacji ciągłej P
Rozdz. 14.3.1 Wstęp
Mam nadzieję, że dokładnie przeczytałeś rozdz13. Najważniejsze są wnioski z wzorów z Rys.13-5. A zwłaszcza to, że przy skoku wartości zadanej x(t)=1(t) sygnał wyjściowy w stanie ustalonym  y=K*x/(1+K). Np. dla K=10 wyjście y=0.91. Ogólnie, im większe K, tym bardziej bardziej y zbliża się do x. Tak będzie dla regulacji typu P. Dla regulacji I, PI i PID jest jeszcze lepiej. Wyjście ustalone y zrówna się z wartością zadaną x. Niezależnie od zakłóceń na obiekt! Taki jest główny cel Automatyki.
Rozdz. 14.3.2 Regulacja P bez zakłócenia
Przy okazji porównamy układ bez regulacji-y1(t) i z regulacją-y2(t). 

Rys.14-3
Regulacja P dla członu inercyjnego-odpowiedź na skok 
Widzisz 2 takie same obiekty z wyjściem y1(t) i y2(t). A po co to? Abyś porównał ten sam obiekt w układzie otwartym i zamkniętym. Obiekt z y2(t) jest sterowany przez regulator typu P, którego jedyną nastawą (parametrem) jest wzmocnienie Kp=10. Po animacji Rys. 14-3 oraz Rys. 13-3 i wzorów Rys. 13-5 z rozdz.13, dojdziesz do wniosku, że y2(t) szybciej dochodzi do stanu ustalonego. Co prawda, jest nim y2=0.91x, a nie y2=x. Czyli uchyb e=0.09 nie jest zerowy! Za to w układzie otwartym, który jest wołowaty, uchyb e=0. Jest to cel każdego automatyka! Tu mogą pojawić się wątpliwości co do układu zamkniętego, który nie daje zerowego uchybu ustalonego e! Znikną w następnym podrozdziale.
Rozdz. 14.3.3 Regulacja P z zakłóceniem z(t)=+0.2
Ten sam obiekt co poprzednio i z takim samym regulatorem P, gdy Kp=10. Jedyna różnica to zakłócenie dodatnie z(t)=+0.2, które pojawi się w 70 sekundzie. To tak jakbyś włożył do pieca grzałkę, która w układzie bez regulacji podniosłaby temperaturę pieca o ΔT=+20ºC. Przebieg trwa 2 minuty, dlatego proszę o cierpliwość. 

Rys.14-4
Regulacja P-Odpowiedź na skok i zakłócenie z(t)=+0.2 
Zakłóceniem z(t) jest tu dodatkowe grzanie +0.2. Tak jakby się pojawiła dodatkowa grzałka, albo skoczyło napięcie na grzałce.
Do 70 sek. jest tak jak na Rys. 14-3. Na zakłócenie z(t)=+0.2 w 70 sek. regulator zareagował prawidłowo. Obniżył moc grzania na grzałce za regulatorem. Co prawda widać niewielki wpływ zakłócenia, ale został on 11-krotnie stłumiony. Całkowite tłumienie, jak się później przekonasz, zapewni nam tylko regulacja z całkowaniem uchybu e(t) czyli typu I, PI lub PID.
Rozdz. 14.3.4 Regulacja P-Wnioski
1. Sprzężenie zwrotne poprawia dynamikę, tym bardziej im większe wzmocnienia regulatora Kp
2. Pamiętasz wątpliwości z Rozdz. 14.2.2? Układ zamknięty poprawiał dynamikę 11-krotnie, za to przy skoku jednostkowym wprowadzał stały uchyb e=0.09. Ale był on 11 razy mniejszy, niż bez regulatora! 
3. Zwróć uwagę na sygnał sterujący s(t). Bez zakłócenia i w stanie ustalonym, czyli w okresie 10…70 sek, sygnał s(t)=y(t). Jest to typowe dla każdej regulacji P, I, PI i PID. Po 70 sekundzie s(t) spada, starając się skompensować zakłócenie +z(t). Chociaż nie sprowadza uchybu do 0, to jednak znacząco go tłumi. Jest to typowe dla regulacji P.
4. Regulacja P szybko reaguje na wejście x(t), i szybko, chociaż nie do końca tłumi stałe zakłócanie.
5. Jednak chciałbyś mieć regulację, która sprowadza uchyb stały e do zera.
To czytaj dalej.

Rozdz. 14.4 Układ regulacji ciągłęj I-tylko z całkowaniem
Rozdz. 14.4.1 Wstęp
Regulator I jest rzadko stosowany w praktyce. Natomiast idealnie nadaje się do celów dydaktycznych. Łatwiej zrozumiesz w nim zasadę sprzężenia zwrotnego i tłumienie zakłóceń niż w regulatorze P. Zwłaszcza to, że potrafi sprowadzić uchyb regulacji e do zera! To dlaczego nie jest stosowany w praktyce. Bo jest wołowaty. Tzn. bardzo wolno dochodzi do stanu ustalonego.
Rozdz. 14.4.2 Badanie regulatora I

Rys.14-5
Odpowiedź na skok jednostkowy regulatora I (całkującego)
Najważniejszym elementem każdego regulatora jest węzeł porównujący wykonujący odejmowanie e(t)=x(t)-y(t). Dlatego sygnał x(t) na Rys.14-5 traktuj jako uchyb e(t)! Czyli założyliśmy, że y(t)=0. Regulator bez węzła porównującego byłby bez sensu. Regulatot I ma tylko jedną nastawę, czas całkowania tu Ti=2sek. Jest to czas po którym wyjście z regulatora y(t) zrówna się z wartością skoku x(t) na wejściu. Tu po 2 sekundach. Czyli im większe Ti,  tym wolniej narasta sygnał z regulatora I. Narysuj w XCOSie regulator I i zbadaj go przy różnych wartościach skoku x(t) i różnych nastawach Ti.
Uwaga
Blok całkujący 1/2s otrzymamy z bloku CLR z palety “Systemy czasu ciągłego”. Zmień mianownik z 1+s na 2*s
Rozdz. 14.4.3 Regulacja I z zakłóceniem z(t)=+0.5
Znowu musisz uzbroić się w cierpliwość. Przebiegi z regulacji z I trwają długo, tu 4 min.

Rys.14-6
Regulacja I-Odpowiedź na skok i zakłócenie z(t)=+0.5 
W odróżnieniu od Regulacji P w odpowiedzi na skok i na zakłócenie skokowe uchyb regulacji w stanie ustalonym jest zerowy, tzn. e=0. Zwłaszcza pięknie widać reakcję na zakłócenie dodatnie z(t)=+0.2. W momencie pojawienia się zakłócenia, y(t) stara się rosnąć do y=1.5. Ale zaraz zadziała ujemne sprzężenie zwrotne. Składowa całkująca dotąd będzie kompensować zakłócenie, aż zrobi to całkowicie gdy e=0. Chciałoby się powiedzieć, dotąd będzie wiercić dziurę w brzuchu…
Jeżeli cudowne własności składowej I nie przekonały Cię, to zrobi to Rys. 25-6 w rozdz. 25 kursu ‘Podstawy Automatyki”.
Rozdz. 14.4.4 Wnioski
Jest tylko jeden. W odpowiedzi na skok i zakłócenie Regulacja I sprowadza uchyb e do zera. Robi to jednak bardzo wolno w porównaniu do Regulacji P. Dlaczego? Porównaj reakcję sterowania s(t) w chwili początkowej skoku z “kopem” na Rys. 14-4 i bez “kopa” na  Rys. 14-6. Właśnie ten kop decyduje o dynamice. Lubię język naukowy.

Rozdz. 14.5 Układ regulacji ciągłej PI-proporcjonalno-całkującej.
Rozdz. 14.5.1 Wstęp
Regulacja P daje szybki przebieg, ale niezerowy uchyb e. Regulacja I odwrotnie, wolny przebieg i zerowy uchyb e. To zróbmy hybrydę tych obu regulatorów-Regulator PI. Spodziewamy się szybkiego przebiegu i zerowego uchybu 
Rozdz. 14.5.2 Odpowiedź regulatora PI na sygnał skokowy x(t).

Rys.14-7
Odpowiedź na skok jednostkowy regulatora PI 
Pamiętaj, że jak w każdym regulatorze musi być węzeł porównujący wykonujący operacje e(t)=x(t)-y(t).
Dla prostoty założyliśmy, że y(t)=0 i dlatego badamy tylko x(t). 
Regulator PI ma dwie nastawy-wzmocnienie Kp i czas zdwojenia Ti. 
Wzmocnienie Kp obliczymy wyłączając tor całkowania.
Czas zdwojenia Ti-czas po którym sygnał wyjściowy regulatora dwukrotnie się zwiększy.
Albo inaczej. Czas po którym składowa całkująca yi zrówna się ze składową proporcjonalną yp.
Zrealizuj schemat programem XCOS i pobaw się wejściem x(t) oraz nastawami Kp i Ti.
Okaże się, że Kp i Ti nie zależą od wielkości skoku x(t).
Rozdz. 14.5.3 Regulacja PI z zakłóceniem z(t)=+0.5

Rys.14-8
Regulacja PI-Odpowiedź na skok i zakłócenie z(t)=+0.5 
Kp=10 i Ti=5sek zostały dobrane wcześniej metodą prób i błędów. Mogą być lepsze. Spróbuj.
Porównanie z regulacją typu P na Rys.14-4
Dynamika podobna, chociaż w odpowiedzi na skok jest małe przeregulowanie. Lepiej?, gorzej? Nie wiem. De gustibus non est disputantum. Załóżmy, ze nie jest gorzej ani lepiej.
Za to uchyb zerowy. 
Wniosek
Regulacja PI jest lepsza od P.
A teraz jak to działa?
Na początku skoku wejścia x(t) w 3 sekundzie lub zakłócenia z(t) w 70 sekundzie działa głównie składowa proporcjonalna regulatora. Dlatego sygnał y(t) szybko zbliża się do wartości ustalonej.  Nie jest to oczywiście wartość skoku x(t), bo regulacja P nigdy nie zapewni zerowego uchybu ustalonego e=0. To jest zadanie dla składowej całkującej I. Na początku nie widać jej wpływu, bo ten sygnał dopiero narasta. Widać go później, gdy składowa P przestanie mieć wpływ. Wtedy składowa całkująca, zgodnie ze swoją rolą, sprowadzi uchyb do zera tj. e=0. Dotyczy to skoku wartości zadane  x(t) i skoku zakłócenia z(t). Podsumowując. Składowa całkująca dotąd będzie wierciła dziurę w brzuchu aż sprowadzi uchyb e(t) do zera. Zauważ, że w stanie ustalonym zakłócenie z(t)=+0.5 jest kompensowane przez sygnał sterujący regulatora Δs(t)=-0.5.
Rozdz. 14.5.4 Wnioski
1. Dynamika regulacji PI jest porównywalna z regulacją P. 
2. Regulacja PI może sprowadzić uchyb regulacji do zera, czego nie zapewnia Regulacja P.
3. Optymalne nastawy Kp i Ti to takie które zapewnią w miarę szybki i bez przeregulowań sygnał y(t) w odpowiedzi na x(t) lub z(t). Okaże się, że “ładna” odpowiedź na x(t), to często “brzydka” odpowiedź na z(t) i vice versa. Rolą projektanta jest dokonanie właściwego wyboru. W zależności od tego co pojawia się częściej. Zmiana x(t) czy zakłócenia z(t)? Uwaga dotyczy też regulacji PD i PID.

Rozdz. 14.6 Układ Regulacji ciągłej PD czyli proporcjonalno-różniczkującej.
Rozdz. 14.6.1 Wstęp
Składowa różniczkująca reaguje na prędkość sygnały wejściowego e(t). W stanie ustalonym nie ma żadnych prędkości, czyli daje sygnał zerowy. Czyli nie jest w stanie zlikwidować stałego uchybu regulacji e. Natomiast znakomicie poprawia dynamikę przebiegu.
Rozdz. 14.6.2 Badanie członu różniczkującego rzeczywistego. Czyli D inercją.

Rys.14-9
Odpowiedź członu różniczkującego rzeczywistego na sygnał narastający liniowo.
W pewnym momencie prędkość sygnału wejściowego wzrośnie dwukrotnie. 
Traktuj człon różniczkujący jako prędkościomierz, który mierzy prędkość z pewną inercją. Im tańszy (gorszy) tym inercja większa. Widać jak wyjście zwiększyło się dwukrotnie, gdy prędkość zwiększyła się dwukrotnie.
Z inercją T=0.1sek oczywiście. Sygnał ustalił się po czasie ok. 4T. 
*Zwykle badamy odpowiedź członu na skok jednostkowy. Ale dla członu różniczkującego D lepszym będzie sygnał narastający liniowo, czyli ze stałą prędkością. Dlaczego? Bo przy skoku jednostkowym prędkość narastania jest nieskończenie wielka i powstają z tego różne problemy. 
Jeszcze jak obliczyć parametry tego bloku. Z transmitancji 1*s/(1+0.1*s) banalnie Td=1sek i T=0.1sek. 
A z wykresu? Tak jak na animacji. Oczywiście zgadza się. Pamiętaj tylko, że przecięcie linii y(t) i x(t) ma być dla ustalonego y(t)!
Rozdz. 14.6.3 Odpowiedź regulatora PD rzeczywistego na sygnał narastający liniowo.

Rys.14-10
Odpowiedź na sygnał narastający liniowo regulatora PD (z różniczkowaniem rzeczywistym)
Kp=1, Td=1sek, T=0.1sek
Po co to różniczkowanie rzeczywiste z inercją T=0.1sek. Chyba nie poruszałem tego tematu. Bo różniczkowanie idealne wprowadza “szpilki” przy szybkich zmianach x(t), co niekorzystnie wpływa na regulację. Inercja T tłumi te zakłócenia. Ale wróćmy do wątku głównego.
„Wygładzenia” po 1 i 5 sekundzie (wtedy występuje zmiana prędkości sygnału x(t)) wynikają z tego, że tor różniczkujący rzeczywisty potrzebuje ok. 0.5 sek żeby „dojść do siebie” i obliczyć właściwą prędkość. Wstanie ustalonym dobrze widać składową proporcjonalną P i D która jest taka sama jak dla idealnego członu PD. Podkreślam-taka sama, ale tylko w stanie ustalonym.
Uwaga:
W pierwszej chwili wydaje się, że reakcja na sygnał narastający x(t) członów P i D jest podobna.
Ale wynika to tylko z tego, że sygnał sterujący y(t) jest sumą
–składowej P, która narasta jak Kp*x(t)
–składowej Kp*D która która jest prawie stała. Oprócz początkowych inercji, oczywiście.
Rozdz. 14.6.4 Regulacja PD z zakłóceniem z(t)=+0.5
Czyli z potężnym zakłóceniem. To tak jakby do pieca włożyć dodatkową grzałkę o połowie mocy grzałki sterującej! Obiektem będzie dwuinercyjny, a nie inercyjny jak poprzednio. Dlaczego? Bo inercyjny jest  obiektem “łatwym” do sterowania. Wystarczy dać duże Kp aby odpowiedź była cacy. Innymi słowy, nie sztuka być bokserem z łatwym przeciwnikiem.

Rys.14-11
Regulacja PD-Odpowiedź na skok i zakłócenie z(t)=+0.5 
Do 30 sekundy jest tylko reakcja na ba wartość zadaną x(t). A po 30 sekundzie reakcja na zakłócenie z(t)=+0.5. No dobrze. Ale jak tu porównać z regulacją P? Z Rys. 14-4 nie można, bo inny obiekt G(s). To porównajmy z odpowiedzią ze sterowaniem P i tym samym obiektem.
Rozdz. 14.6.5 Porównanie regulacji PD i P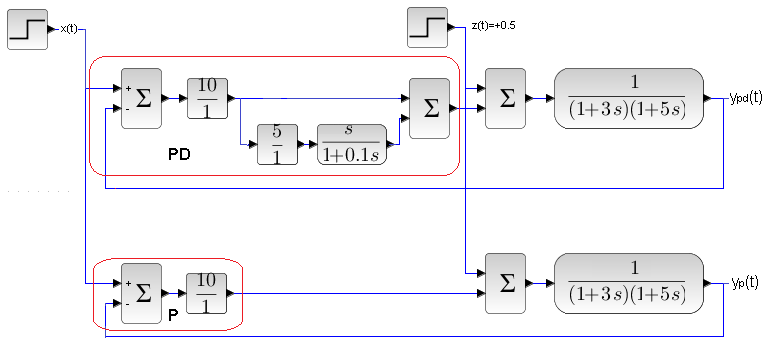

Rys. 14-12
Porównanie PD i P
Takie same obiekty G0(s) i takie same sygnały x(t) i z(t). Ciekawe, kto wygra mecz PD contra P? 

Rys. 14-13
Kto lepszy PD czy P?
Jeżeli chodzi o x(t) to ewidentnie ypd(t) jest lepsze od yp(t). Sygnał ypd(t) prawie natychmiast dochodzi do stanu ustalonego, a yp(t) dopiero po 20 sek. W dodatku z przeregulowaniami. Jak wyjaśnić pozytywny efekt różniczkowania w PD? W w czasie skoku x(t) regulator PD daje potężnego “różniczkującego” kopa od D. Wtedy ypd(t) bardzo szybko narasta. Aż boimy się przeregulowań. Ale wtedy wystąpi “hamujące” działanie składowej D, ponieważ ypd(t) wchodzi z minusem na regulator z PD. To zapobiegnie przeregulowaniom.
W stanie ustalonym jest remis wynikający z tego, że dla PD składowa różniczkująca znika. Czyli P oraz PD nie zapewniają uchybu zerowego. W PD jest za to znacznie lepsza dynamika.
A reakcja na dodatnie zakłócenie z(t)=+0.5 w 30 sek?
I tu jest problem. Bo, chociaż z przeregulowaniami, to yp(t) wydaje się lepsze od ypd(t). Jako adwokat PD podkreśliłbym to “wydaje”. Nie jest to jednak przekonywujące dla sędziego i publiki. To powiem tak. Tu nastawy Kp=10 i D=5sek zostały dobrane ze względu na optymalną reakcję na wejście x(t), a nie zakłócenie z(t). Uwierz jednak,  że można nastroić PD tak, że reakcja na x(t) będzie  trochę wolniejsza, ale nadal dużo szybsza niż dla P. Za ro reakcja na zakłócenie z(t) będzie zdecydowanie lepsza.
Rozdz. 14.6.6 Wnioski
Chociaż obydwie regulacje nie zapewniają zerowego uchybu ustalonego  e, to Regulacja PD jest znacznie szybsza niż P. Należy ją stosować, gdy bardziej zależy nam na szybkości reakcji niż na dokładności. Wyobraź sobie, że bierzesz udział w wyścigu samochodzików-modeli sterowanych radiowo. Czy zależy Ci na tym, żeby jechał dokładnie co do cm po wyznaczonym torze? Czy na tym, żeby w ogóle nie wypadł z toru?

Rozdz. 14.7 Układ regulacji ciągłej PID-proporcjonalno-różniczkująco-całkującej.
Rozdz. 14.7.1 Wstęp
Wiemy już że:
– Regulacja P a tym bardziej PD szybko reaguje na skokową wartość zadaną x(t), ale uchyb ustalony e(t) jest zawsze niezerowy.
– Regulacja PI zapewnia zerowy uchyb regulacji, ale przebieg jest wolniejszy niż dla regulacji P, a tym bardziej PD.
Metoda narzuca się sama. Należy do regulatora PI dodać składową różniczkującą D. Okaże się, że przebieg będzie szybszy. W dodatku układ będzie bardziej stabilny. A co to oznacza? Że można np. zwiększyć wzmocnienie Kp regulatora, dzięki czemu przebiegi będą jeszcze szybsze. Zaczniemy od badania struktury regulatora PID
Rozdz. 14.7.2 Odpowiedź regulatora PID na sygnał skokowy x(t).
To jeszcze nie regulator, bo nie realizuje jego najważniejszej funkcji, czyli  porównania e(t)=x(t)-y(t). Na razie wejściem jest tylko x(t) i badamy samą dynamikę.

Rys.14-14
Człon PID
Kp=1 Ti=10 sek Td=1 sek
Realizowane 3 składowe sterujące:
-proporcjonalna sP(t)
-całkująca sI(t)
-różniczkująca sD(t)
Sygnałem wejściowym jest skok jednostkowy x(t).
Sygnał sPID(t) regulatora jest sumą składowych sP(t) sI(t) i sD(t).
Składowa proporcjonalna sP(t) to x(t) ponieważ Kp=1.
Składowa całkująca sI(t) narasta z taką prędkością, że po czasie Ti=10 sek zrówna się składową proporcjonalną sP(t). Tu akurat w 13 sekundzie, której nie widać bo doświadczenie kończy się w 10 sekundzie.
Składowa różniczkująca sD(t) – W 3 sekundzie występuje skok x(t) czyli w tym czasie prędkość jest nieskończenie wielka. I takie byłoby sD(t) dla idealnego człon różniczkującego D. A on jest rzeczywisty! Czyli „spłaszczony” przez człon inercyjny o stałej czasowej Td=0.1 sek. Ze względu na zakłócenia rzadko stosowany jest idealny człon różniczkujący D.
Składowe sP(t) i sI(t) są łatwe do interpretacji, gdy sygnał wejściowy x(t) jest skokiem. Gorzej jest z sD(t) ponieważ dla t=3 sek prędkość sygnału jest nieskończenie duża. Dlatego przeanalizujmy jeszcze raz PID, gdy x(t) narasta liniowo.
Rozdz. 14.7.3 Regulacja PID z zakłóceniem z(t)=+0.5 z(t), Kp=10, Ti = 7 sek, Td=1.5 sek

Rys.14-15
Regulator optymalny ze względu na x(t) Zakłócenie z(t)=+0.5 pojawi się w30sekundzie. Do 30 sekundy, jest tylko tylko reakcja na x(t). Początkowo zakłócenie z(t)=+0.5 spowodowało wzrost sygnału y(t), ale potem sygnał sterujący sPID(t) „zmusił” y(t) do powrotu do poprzedniej wartości, czyli do y(t)=1. Odpowiada to odpowiedniemu sprowadzeniu uchybu e(t) do 0. Pięknie widać, jak na dodatkowe grzanie z(t)=+0.5 regulator PID w stanie ustalonym zareagował chłodzeniem sPID(t)=-0.5. Składowa D poprawia dynamikę przebiegu.
Uwaga!
W odpowiedzi na zakłócenie z(t)=+0.5, sygnał sterujący sPID(t) pokrywa się w stanie ustalonym z zakłóceniem z(t)=+0.5. 
Rozdz. 14.7.4 Porównanie regulatorów P, PD, PI i PID
Porównamy regulacje P, PD, PI i PID podając jednocześnie skok x(t) na 4 układy regulacji sterujące tym samym obiektem co na Rys.14-15.  Zostały dobrane optymalne nastawy regulatorów.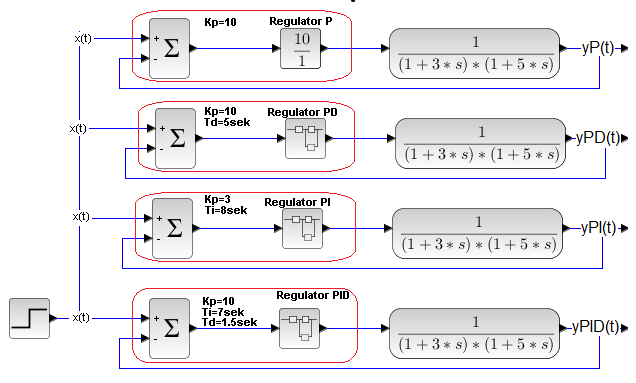

Rys.14-16
Schemat do porównania regulacji P, PD, PI i PID
Domyślamy, która regulacja jest najlepsza. 

Rys.14-17
Porównanie regulatorów P, PD, PI i PID
Czarne yP(t) regulacji P jest najgorsze. Ma najwięcej oscylacji, trwa długo i nie zapewnia zerowego uchybu
Zielone yPD(t) regulacji PD ma najlepszą dynamikę – odpowiedź prawie prostokątna. Też nie zapewnia zerowego uchybu.
Niebieskie* yPI(t) regulacji PI zapewnia już zerowy uchyb, ale długi czas regulacji i oscylacje
Czerwone yPID(t) ma najwięcej zalet. Zerowy uchyb, krótki czas regulacji i małe oscylacje.
Porównaj zwłaszcza efekty pracy wypasionego regulatora PID i jego ubogiego krewnego P.
* Nie bardzo widać, że to niebieskie.