Szeregi Fouriera klasycznie

Rozdział 3 Zespolony szereg Fouriera

Rozdział 3.1 Funkcja zespolona exp(jωt) jako wirujący wektor
W automatyce, elektrotechnice i w wielu innych dziedzinach ciągle pojawia się funkcja zespolona exp(jωt). Jest to szczególny przypadek funkcji zespolonej dla której dziedziną jest liczba rzeczywista czas t, a nie dowolna liczba zespolona z–>Uwaga
Czyli każdej liczbie rzeczywistej t przyporządkowana jest liczba zespolona z=exp(jωt).

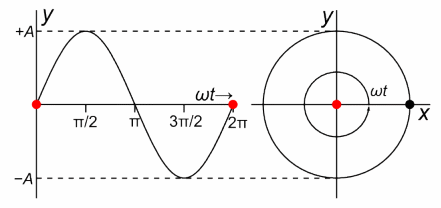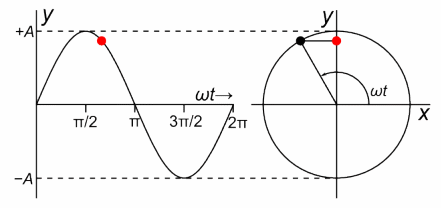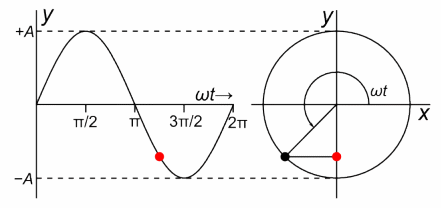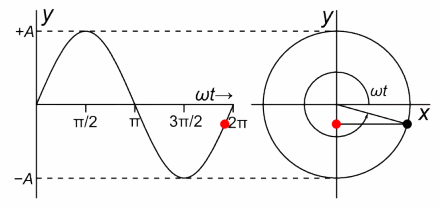
Fig. 3-1
Funkcja zespolona z=1exp(jωt) jako wirujący wektor gdzie ω=2.62/sec author Chetvorno
Po  prawej stronie  zobaczysz płaszczyznę zespoloną z o współrzędnych x,y które potraktuj jako współrzędną rzeczywistą  Re z i urojoną Im z. Punkt z wiruje z okresem T=2.4sek  czyli z prędkością kątową ω=2.62/sek. Sprawdź to zegarkiem, mierząc np. czas 10 obrotów. Położenie obracającego punktu w czasie t, to właśnie dokładnie punkt z=1exp(jωt). Np. dla ωt=0 sek położenie z=1+j0 ,a dla ωt=π/3=60º jest jak  na Rys. 3-1. Ot, takie sobie 2 fotografie pstryknięte w 2 różnych czasach t.
Położenia możesz też obliczyć korzystając ze wzoru Eulera:
exp(jωt)=cos(ωt)+jsin(ωt)
Np. dla ωt=0 i ωt=π/2=90º są to punkty na rysunku zaznaczone strzałką:
z=exp(j0)=1+j0
z=exp(jπ/2)=0+j1
Im większe ω tym szybciej obraca się czarny punkt.
Po  lewej stronie  zobaczysz ruch czerwonej kropki, która jest rzutem wirującego czarnego punktu na oś y. Jest to tzw. ruch harmoniczny opisany funkcją y=sin(ωt). 
Uwaga
W przypadku ogólnym dziedziną funkcji zespolonej jest dowolna liczba zespolona z czyli dwuwymiarowa płaszczyzna zespolona, a przeciwdziedziną też jest dwuwymiarowa płaszczyzna zespolona. Wchodzimy więc w trudniejszą do wyobrażenia przestrzeń czterowymiarową. Na szczęście w technice dziedziną funkcji zespolonej najczęściej jest jednowymiarowy czas t.
Więcej o liczbach i funkcjach zespolonych w artykule “Liczby zespolone” w górnej zakładce.

Rozdział 3.2 Wersja zespolona wyrażenia a*sin(ωt)+b*cos(ωt)
Przy pomocy liczb zespolonych łatwiej wykonuje się obliczenia z funkcjami trygonometrycznymi.
Przykłady
1. Trygonometryczny wzór na a*sin(ωt)+b*cos(ωt) jest bardzo skomplikowany. W wersji zespolonej to zwykłe dodawanie.
2. Różniczkowane i całkowanie w wersji zespolonej to tylko obrót o +/-90º.

Rozdział 3.2.1 Funkcja zespolona c*exp(jωt) jako wirujący wektor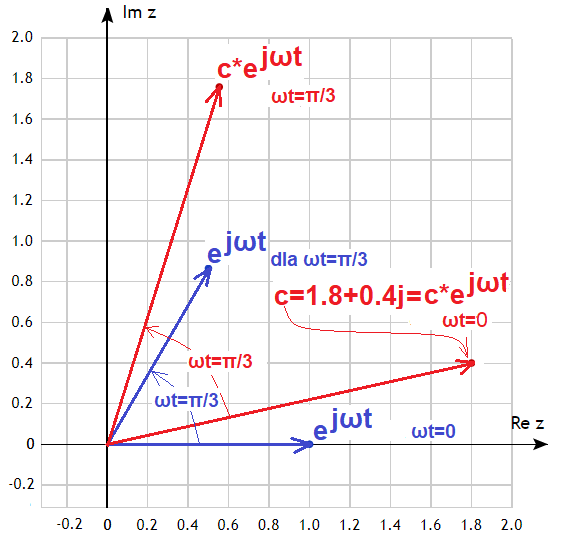

Rys. 3-2
c*exp(jωt) jako wirujący wektor
Wiemy już, że exp(jωt) jest wirującym wektorem o długości 1. Jest to niebieski wektor w stanie początkowym dla ωt=0 oraz po czasie t, tu np. odpowiadającym ωt=π/3=60º. Jest oczywiste, że 2*exp(jωt) będzie wektorem o długości 2, zaś 3*exp(jωt) o długości 3 itd… A co z wyrażeniem c*exp(jωt), gdy c jest liczbą zespoloną np. c=1.8+0.4j? Wektor c*exp(jωt) też będzie będzie wirował. Stanem początkowym jest właśnie c jako c*exp(jωt) dla ωt=0, a po czasie odpowiadającym  ωt=π/3=60º wektor też się się obróci o 60º jak na rysunku.

Rozdział 3.2.2 Składowe a1cos(1ωt) i b1sin(1ωt) jako wirujące wektory
Weźmy pod uwagę składowe a1cos(1ωt) i b1sin(1ωt) ze wzoru Rys. 3-3
Ułatwią nam przejście z Trygonometrycznego szeregu Fouriera na zespolony szereg Fouriera.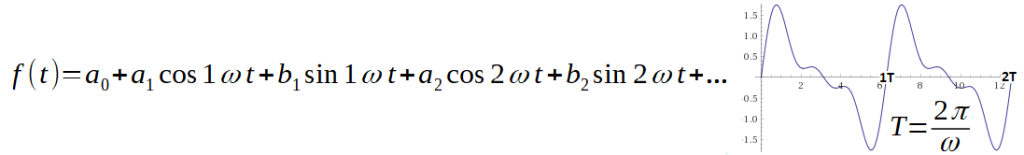

Rys.3-3
Składowa a0 jest stałą, zaś a1,b1,a2,b2… to  amplitudy cosinusoid/sinusoid. Pulsacja 1ω odpowiada okresowi T funkcji f(t).
Jeżeli parametry a0,a1,b1,a2,b2… są dowolne to mamy wzór na sumę cosinusoid/sinusoid o pulsacjach 1ω, 2ω, 3ω… i  amplitudach a1,a2…b1,b2…
Jeżeli współczynniki są ze wzoru Rys. 2-12 z Rozdziału 2.2, to f(t) jest trygonometrycznym szeregiem Fouriera.
Załóżmy, że a1=1 i b1=0.7 zaś pulsację np. ω=2.62/sek zmierzyliśmy wcześniej stoperem.
Czyli szukamy wirujących wektorów reprezentujących przebieg czasowy 1cos(2.62t)+0.7sin(2.62t).
Wektory możemy też traktować tu jako liczby zespolone.

Rys.3-4
a1cos(1ωt)+b1sin(1ωt) jako rzut sumy wirujących wektorów (a1-jb1)exp(jωt) na oś rzeczywistą Re z.
Rys. 3-4a
Wirujące wektory w stanie początkowym, czyli dla 1ωt=0. 
a1
-jb1
suma a1-jb1–>patrz*Uwaga
Rys. 3-4b
Wirujące wektory i ich suma po czasie t.Tu akurat t jest takie, że 1ωt=π/3=60º.
Po czasie t wirujące wektory to:
a1*exp(jωt)
-jb1*exp(1jωt)
(a1-jb1)*exp(j1ωt)
Najważniejszy wniosek
Wyrażenie a1cos(1ωt)+b1sin(1ωt) ze wzoru Rys. 3-1a to rzut wirującego wektora (a1-jb1)*exp(exp(j1ωt) na oś liczb rzeczywistych!
Albo inaczej
a1cos(1ωt)+b1sin(1ωt) =Re z{ (a1-jb1)*exp(j1ωt)}
Dowodem tego jest szkolna trygonometria z Rys. 3-4b gdzie długości wirujących wektorów niebieskiego i zielonego
to a1=1 i b1=0.7.
Wirującym wektorom odpowiadają poniższe przebiegi czasowe.

Rys. 3-5
Przebiegi czasowe  odpowiadające wirującym wektorom z Rys. 3-4
Przebieg 0.7cos(1ωt) jest opóźniony o 90° względem1cos(1ωt) a ich suma 1.22cos(1ωt-35°) jest opóźniona o 35°. Porównaj z wirującymi wektorami na Rys. 3-4.
*Uwaga
Liczbę tę możemy też przedstawić w postaci modułu |c1|≈1.221 i fazy φ≈-35º lub równoważnie w postaci Eulera 1.221*exp(-j35º).
Moduł 1.221 to Pitagoras z 1 i 0.7 zaś φ1=arctg(-0.7/1)≈-35º.  Sprawdź kalkulatorem.

Rozdział 3.3  Zespolony szereg Fouriera dla 3 harmonicznych
Rozdział 3.3.1 Wersja z rzutem na oś rzeczywistą.
Zaczniemy od szeregu Fouriera w którym f(t) ma tylko  3  harmoniczne. Tak będzie łatwiej:
f(t)=a1cos(1ωt)+b1sin(1ωt)+a2cos(2ωt)+b2sin(2ωt)+a3cos(3ωt)+b3sin(3ωt)
Tu mogą pojawić się wątpliwości.
Po pierwsze
Po co rozbijać na szereg Fouriera funkcję f(t) która sama jest szeregiem Fouriera? Współczynniki a0, a1,b1,a2,b2 i a3,b3 widać w funkcji f(t) i nie musisz już korzystać ze wzorów z Rys. 2-12 z poprzedniego rozdziału. Tak, ale robimy to tylko ze względów dydaktycznych. Zresztą, gdyby uwierało, to potraktuj f(t) jak każdą inną funkcję i wstaw ją do wzoru z Rys. 2-12. Otrzymasz tę samą funkcję f(t)!
Po drugie
Dlaczego jest tu 6 składowych a nie 3 jak w tytule?- Bo każda pojedyncza harmoniczna ma składową cosinusową i sinusową.
Na konkretnym przykładzie wygląda to tak:
f(t)=1cos(1ωt)+0.2sin(1ωt)+0.6cos(2ωt)+0.4sin(2ωt)+0.4cos(3ωt)+0.4sin(3ωt)
czyli
a1=1 b1=0.2
a2=0.6 b2=0.4
a3=0.4 b3=0.4
Pozostałe współczynniki a0,a4,b4,a5,b5…=0
Podstawowa pulsacja ω może być dowolna, ale jeżeli lubisz konkret, to załóż ω=2.6.2/sek tak jak w animacji Rys. 3-1.
Współczynnikom c1, c2, c3 można przyporządkować wektory-liczby zespolone:
c1=a1-jb1=1-0.2j
c2=a2-jb2=0.6-0.4j
c3=a3-jb3=0.4-0.4j
Zaś funkcji f(t) wirujące wektory-liczby zespolone
c1*exp(j1ωt)
c2*exp(j2ωt)
c3*exp(j3ωt)
Z Rys. 3-4 wynika:
a1cos(1ωt)+b1sin(1ωt)=Re z {(a1-jb1)*exp(j1ωt)} —>czyli część rzeczywista wirującego wektora (a1-jb1)*exp(j1ωt)
Analogicznie dla 2ωt,3ωt
a2cos(2ωt)+b2sin(2ωt)=Re z {(a2-jb2)*exp(j2ωt)}
a3cos(3ωt)+b3sin(3ωt)=Re z {(a3-jb3)*exp(j3ωt)}
Czyli funkcja czasowa f(t) to część rzeczywista sumy wirujących wektorów
c1*exp(j1ωt)+c2*expj2ωt)+c3*exp(j3ωt)
gdzie c1=a1-jb1, c2=a2-jb2, c3=a3-jb3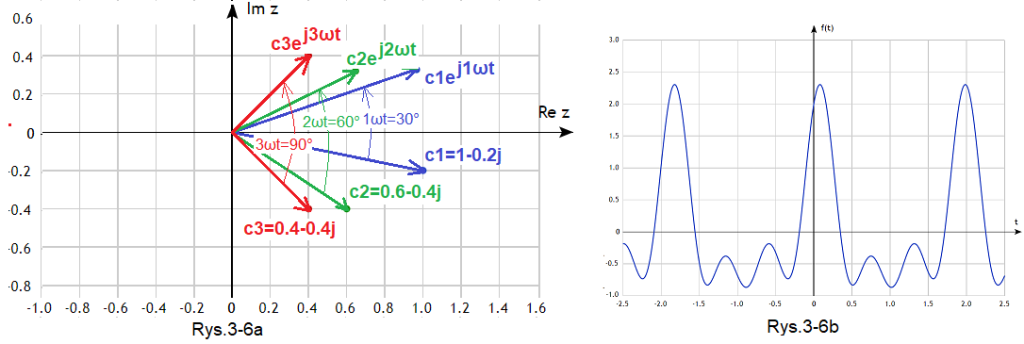

Rys. 3-6
Rys. 3-6a Wirujące wektory odpowiadające funkcji f(t)
Rys. 3-6b Funkcja f(t) jako wynik sumy harmonicznych
c1, c2, c3 to wirujące wektory c1*exp(j1ωt), c2*exp(j2ωt) i c3*exp(j3ωt) w stanie początkowym t=0, oraz po czasie t odpowiadającemu fazom 1ωt=30º, 2ωt=60º i 3ωt=90º. Widać że po tym samym czasie wektor c3, który był najbardziej “opóźniony”, obrócił się najwięcej. Nic dziwnego, skoro ma największą prędkość obrotową 3ωt. Zauważ, że wirujące wektory c1*exp(j1ωt),c2*exp(j2ωt) i c3*exp(j3ωt) mają dla t=0 wartość c1=1-0.2j,c2=0.6-0.4j i c3=0.4-0.4j. Wystarczy podstawić t=0 do wzorów.
Suma rzutów wirujących wektorów na oś Re z jest właśnie funkcją f(t)
Czyli:
f(t)=Re  {c1*exp(j1ωt)+c2*exp(j2ωt)+c3*exp(j3ωt)}
Dwie uwagi
1. Po okresie T wirujące wektory wrócą do stanu początkowegoc1,c2, c3. Tyle tylko że wektor niebieski wykona 1, zielony 2
a czerwony 3 obroty.
2. wyrażenie c1*exp(j1ωt) + c2*exp(j2ωt) + c3*exp(j3ωt) jest zespoloną  funkcją okresową o okresie T=2π/ω.
3. Wirujące wektory przypominają układ słoneczny ze Słońcem w (0,0) i z orbitami:
c1*exp(j1ωt)–orbita Marsa-największa
c2*exp(j2ωt)–orbita Ziemi
c3*exp(j3ωt)-orbita Wenus-najmniejsza
Mars ma najmniejszą prędkość kątową a Wenus największą i  w tym wirujące wektory są podobne do planet.
Rys.3-6 przedstawia poszczególne wirujące wektory, ąle nie widać ich sumy!
Wady tej nie ma wersja z Rys. 3-7 w którym sumą  wirujących wektorów  jest koniec wektora c3*exp(j3ωt). Jest to wygodniejsza metoda dodawania wektorów niż poprzednia “równoległobokowa”!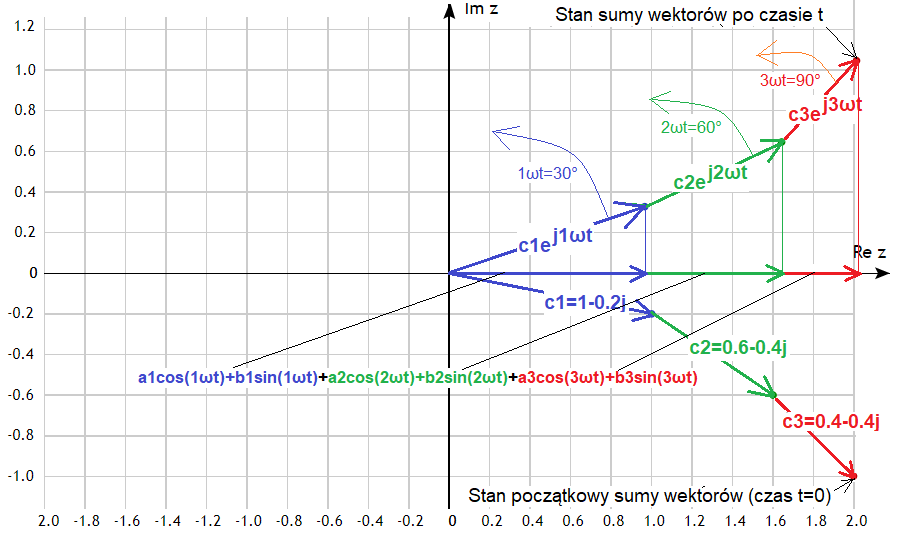

Rys. 3-7
Suma wirujących wektorów c1*exp(j1ωt) + c2*exp(j2ωt) + c3*exp(j3ωt)
Pierwszy niebieski wektor wiruje wokół (0,0), zielony wokół końca niebieskiegoa czerwony wokół końca zielonego. Kolejne prędkości są coraz większe. Przypomina to koniec strzelającego bata przekraczającego barierę dźwięku.
Dolny wektor to stan początkowy dla t=0, a górny to stan po czasie t odpowiadającym fazie 1ωt=30º niebieskiego wektora lub, co na jedno wychodzi dla fazy 2ωt=60º zielonego i 3ωt=90º czerwonego.
Po okresie T gdy:
–niebieski wykona 1 obrót
–zielony 2 obroty
–czerwony 3 obroty
znowu będzie stan początkowy!
Wracając do astronomii to tym razem:
niebieski jest Ziemią krążącą wokół Słońca(0,0)
zielony jest Księżycem krążącym wokół Ziemi
czerwony jest sztucznym satelitą krążącym wokół Księżyca.
Wirującym wektorom c1*exp(j1ωt), c2*exp(j2ωt) i c3*exp(j3ωt) na Rys. 3-7 towarzyszą ich rzuty na oś Re z, czyli:
a1cos(1ωt)+b1sin(1ωt)
a2cos(2ωt)+b2sin(2ωt)
a3cos(3ωt)+b3sin(3ωt)
Dlatego oczywiste jest że:
f(t)=Re (a1-jb1)*exp(1jωt)+(a2-jb2)*exp(2jωt)+(a3-jb3)*exp(3jωt)
czyli
f(t)=Re  c1*exp(1jωt)+c2*exp(2jωt)+c3*exp(3jωt)
Podsumowanie

Rys. 3-8
Zespolony Szereg Fouriera dla f(t) z 3 harmonicznymi
Rys. 3-8a
Wzór ogólny gdy f(t) ma 3 dowolne harmoniczne
Rys. 3-8b
Wzór szczególny gdy f(t) ma 3 konkretne harmoniczne

Rozdział 3.3.2 Wersja przeciwnie wirujących wektorów, inaczej wersja “bez Re z”
Spójrz jeszcze raz na Rys. 3-7. Przedstawia on sumę wirujących wektorów c1*exp(j1ωt)+ c2*exp(j2ωt)+c3*exp(j3ωt) oraz jej rzut na oś Re z, tu dla fazy 1ωt=30º. Czyli c1=1-0.2j obróciło się o 30º. Odpowiada to równaniu z Rys. 3-9a.

Rys. 3-9
2 równoważne wzory na f(t) z 3 harmonicznymi.
Jeżeli we wzorze Rys.3-9a:
1. Wirujący wektor niebieski zastąpimy
– jego  połową–>(0.5-0.1j)exp(j1ωt)
– “sprzężoną połową”—> (0.5+0.1j)exp(-j1ωt) która obraca się w przeciwnym kierunku bo jest -j1ωt!
2. To samo zrobimy z wektorem zielonym i czerwonym.
To otrzymamy równoważny wzór Rys. 3-9b 
Zauważ, że chociaż nowy wzór jest dłuższy, to od razu daje liczbę rzeczywistą!
Rys. 3-9c jest uogólnieniem wzoru Rys. 3-9b. Pamiętaj tylko że, c1, c2 i c3 to połówki c1, c2 i c3 wzoru z Rys. 3-8a!
Podkreślam
Pary wektorów tego samego koloru są wektorami sprzężonymi wirującymi w przeciwnych kierunkach!!!
Interpretacją wzorów Rys.3-9b i Rys.3-9c jest Rys.3-10 z 3 parami przeciwnie wirujących sprzężonych wektorów.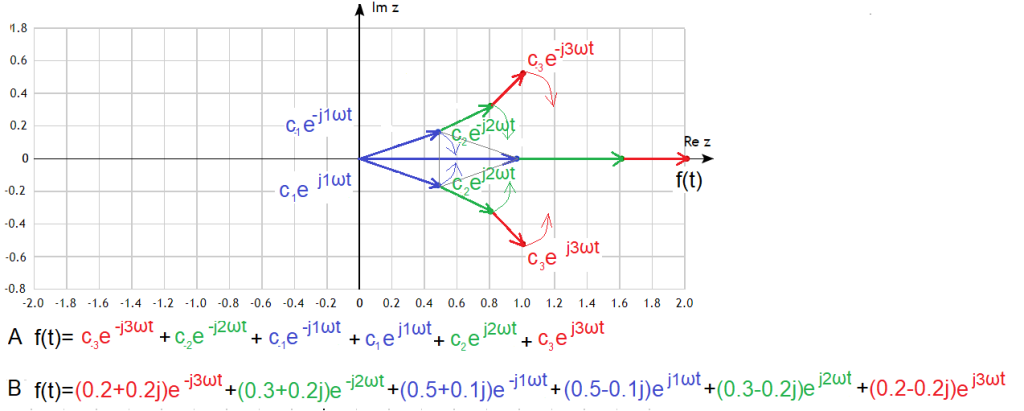

Rys. 3-10
f(t) jako suma wirujących przeciwnie par wektorów
A – wzór ogólny dla dowolnych par wektorów c(-3), c(-2), c(-1), c(1), c(2) i c(3)
B – wzór szczególny dla konkretnych par wektorów
Już na pierwszy rzut oka widać że:
1. Dolne wirujące wektory to połówki dolnych wirujących wektorów z Rys.3-7 dla t=0.
2. Górne i dolne wirujące wektory to liczby sprzężone (“z lustrzanym odbiciem”)
3. Górne i dolne wektory wirują w przeciwnych kierunkach a ich suma to:
f(t)=a1cos(1ωt)+b1sin(1ωt)+a2cos(2ωt)+ b2sin(2ωt)+a3cos(3ωt)+ b3sin(3ωt)
Wyjaśnienie dla p.3
Wzór B to wirujące w przeciwnych kierunkach pary wektorów  o współczynnikach zespolonych c(-1), c1    c(-2),c2 i c(-3),c3 “sfotografowane” na Rys.3-10 w chwili t=0.
Np. para (0.5-j0.1)exp(j1ωt) i (0.5+j0.1)exp(-j1ωt) daje sumę = niebieski wektor na osi Re z.   Jest on równy niebieskiemu poziomemu wektorowi na osi Re z na Rys.3-10 czyli 1cos(1ωt)+0.2sin(1ωt). Wektor ten będzie poruszał zgodnie z tym wzorem tylko po osi Re z.
Analogicznie jest z wirującą parą zieloną i czerwoną.
Suma wszystkich wirujących wektorów da nam szczególny wzór B i ogólny wzór A.

Rozdział 3.4  Zespolony szereg Fouriera-wzór ogólny z częścią rzeczywistą
Rozdział 3.4.1 Podstawy
A teraz najważniejsze
1. Weź dowolną funkcję okresową f(t) o okresie T
2. Oblicz pulsację podstawową ω=2π/T
3. Oblicz współczynniki a0,a1,b1,a2,b2,…an, bn…  a następnie współczynnik rzeczywisty c0 i zespolone  c1,c2,c3…cn…

Rys. 3-11
Wzory na współczynniki Fouriera
Teraz możemy już wyznaczyć ostateczny ogólny wzór na zespolony szereg Fouriera z częścią rzeczywistą.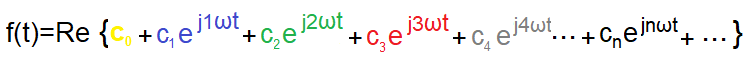

Rys. 3-12
Wzór jest  uogólnieniem Rys.3-8a. Pojawiła się składowa stała c0. Niezbyt widoczna bo żółtego koloru.
Dokładnie przybliża funkcję f(t) tylko dla n=∞, ale praktycznie wystarczy kilkanaście, może trochę więcej, pierwszych składowych.
Każdy składnik c1*exp(1ωt), c2*exp(2ωt),, c3*exp(3ωt), c4*exp(4ωt), c∞*exp(∞ωt) jest wirującym wektorem tak jak na Rys. 3-13.

Rys.3-13
Żółty wektor c0 jest składową stałą i jako jedyny nie wiruje. Albo formalnie wiruje, ale z pulsacją ω=0. Pozostałe wirują coraz szybciej “każdy wokół końca poprzedniego” czyli pośrednio wokół końca stałego c0. Kolejne wektory są coraz krótsze, a ostatni c∞ ma najczęściej długość zerową i wiruje nieskończenie szybko! Im bliżej c∞ tym łamana na Rys.3-13 zbliża się do linii ciągłej! Rzut końca ostatniego wektora na oś rzeczywistą jest właśnie naszą funkcją okresową f(t). Spróbuj sobie wyobrazić te wirujące wektory. Czy nie przypomina Ci to koniec strzelającego bata?
Innymi słowy
Wektory sobie wirują a rzut punktu c∞ na oś rzeczywistą, porusza się dokładnie tak jak funkcja f(t)!
Tak jak nie ma ideałów w życiu, tak ostatnim wirującym wektorem jest np.  c20*exp(j20ωt) a nie c∞*exp(j∞t). To już w zupełności wystarcza, żeby w miarę dokładnie przybliżyć funkcję f(t).
Uwaga:  “Ostatni” wirujący  c∞*exp(j∞t) ma najczęściej długość zerową. Ale suma wszystkich wirujących wektorów, czyli punkt który wskazuje c∞*exp(j∞t), jest najczęściej skończony! Przekonasz się o tym za chwilę!

Rozdział 3.4.2 Przykład z falą prostokątną
Nic tak nie przemawia do wyobraźni jak konkretny przykład, np. z falą prostokątną. Został on dokładnie omówiony w rozdziałach 2.5 i 2.6 jako szereg trygonometryczny.
Wróć tam na chwilę. Fala prostokątna o pulsacji ω=2π (czyli T=1sek) to

Rys. 3-14
Szereg Trygonometryczny fali prostokątnej o ω=2π 1/sek.
Zauważ, że składowa stała c0=0, co jest oczywiste oraz
c2=c4=…=c2n=0 ponieważ fala prostokątna f(t) z Rys. 2-13 jest funkcją nieparzystą. Także współczynniki “cosinusowe” są zerowe b1=b2=b3=0….
Ze współczynników przy sinusach/cosinusach na Rys. 3-14 oraz ze wzorów Rys. 3-11 wynika bezpośrednio że:
c1=-4j/π, c3=-4j/3π, c5=-4j/5π, c7=-4j/7π 
i szereg trygonometryczny Fouriera fali prostokątnej może być też przedstawiony jako  szereg zespolony Fouriera.
Zauważ, że nawet nie musiałeś liczyć całek. Ale gdybyś się uparł, bo lubisz 2 grzyby w barszczu, to podstawieniu f(t) z Rys. 3-14 do wzoru Rys. 3-11 wynik byłby identyczny.

Rys. 3-15
Zespolony Szereg Fouriera fali prostokątnej
Stan początkowy, czyli dla t=0 to kolejne pionowe wektory na dolnej półosi urojonej Re z.  Widoczne są tylko 4 pierwsze, jako c1,c3,c5 i c7. Wektory  “parzyste” c0,c2,c4,c6…, jak stwierdziliśmy wcześniej, są zerowe. Ostatni c∞, chociaż jego długość jest zerowa, leży w nieskończoności na ujemnym “końcu” osi urojonej Im z.  Tu przeczytaj uwagę końcową poprzedniego podrozdziału.
Pokazałem także stan wektorów gdy c1 obrócił się o 1ωt=60º, c3 o 3ωt=180º, c5 o 5ωt=300º, a c7 o 7ωt=420º. Ewidentnie wektor c7exp(7jωt) jako najszybszy wykonał największy obrót (420º tj. pełen obrót+60º), zwłaszcza w porównaniu do najwolniejszego c1exp(1jωt). A jak odczytać f(t) jako sumę obracających się wektorów? Proszę bardzo, dla t=0 jest to rzut na oś Re z czyli f(0)=0, a dla t odpowiadającemu obrotowi 1ωt=60º=π/6 też jest w przybliżeniu rzutem końca wektora c7exp(7jωt) na Re z.
Dlaczego w przybliżeniu? Bo nie uwzględniłem jeszcze pozostałych wektorów  c9exp(9jωt)…c∞exp(∞jωt) kończących się w skończonym punkcie c∞. Ten punkt leży gdzieś w pobliżu końca wektora c7exp(7jωt) i musisz go sobie jakoś wyobrazić. Tylko rzut tego wektora daje idealną falę prostokątną.
Rozpatrzmy jeszcze raz wykres z Rys. 3-16. Dla prostoty załóżmy że nasza funkcja f(t) ma tylko  3 pierwsze  harmoniczne czyli będą wirować tylko 3 wektory c1,c3,c5 z prędkościami 1ωt, 3ωt i 5ωt.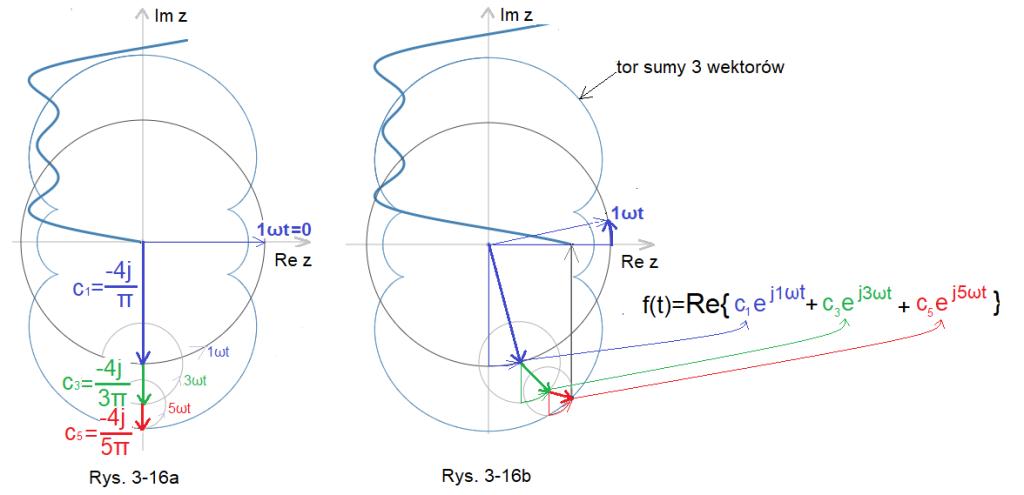

Rys. 3-16
Rys. 3-16a Stan początkowy dla fazy 1ωt=0.
Rys. 3-16b Stan dla fazy 1ωt. Wektor c5exp(j5ωt) wiruje wokół końca c3exp(j3ωt) który z kolei wiruje wokół końca c1exp(j1ωt). Przypomina to układ ze Słońcem w punkcie (0,0), Ziemią obracającą się wokół Słońca, Księżyca wokół Ziemi i Satelity wokół Księżyca. Po czasie odpowiadającym 1ωt=2π  znowu będzie stan początkowy jak na Rys. 3-16a z tym że “Ziemia” wykona 1, “Księżyc” 2 a “Satelita” 3 obroty.
Rzut “Satelity” na oś Re z porusza się dokładnie ze wzorem f(t)=Re { c1exp(j1ωt)+c3exp(j3ωt)+c5exp(j5ωt)}.
Są to 3 pierwsze “niezerowe” harmoniczne rozkładu fali prostokątnej na Trygonometryczny Szereg Fouriera.
Zaś samo wyrażenie c1exp(j1ωt)+c3exp(j3ωt)+c5exp(j5ωt) są to 3 pierwsze składowe Zespolonego Szeregu Fouriera fali prostokątnej.
Zauważ, że tor Satelity wokół Słońca  (a nie wokół Księżyca) nie jest już okręgiem lecz jakimś dziwnym wygibasem! Okazuje się, że przy odpowiedniej kombinacji współczynników  zespolonych cn i dużym n Satelita będzie obracała się po dowolnym torze. Nawet kwadratowym! Czyli dając odpowiednie cn możemy rysować dowolne obrazy. Tym zajmuje się od niedawna teoria przetwarzania obrazów.  Fourier chyba się w grobie przewraca.
Uwaga
Okrąg na Rys. 3-1 jest funkcją przyporządkowującą każdemu czasowi t odpowiedni punkt z=1exp(jωt) na płaszczyźnie liczb zespolonych z.
Analogicznie
Tor sumy 3 wektorów na Rys. 3-16 jest funkcją przyporządkowującą każdemu czasowi t odpowiedni punkt z=c1exp(j1ωt)+c3exp(j3ωt)+c5exp(j5ωt) na płaszczyźnie liczb zespolonych z.

Rozdział 3.4.3 Animacja (z youtube)
Kliknij trójkącik “play” youtube’a. Nick autora GLV.

Fig. 3-17
Animacja Zespolonego Szeregu Fouriera fali prostokątnej
Wirujące 4 górne wektory to  4 składowe ze wzoru
f(t)=Re{c0+c1exp(j1ωt)+c3exp(j3ωt)+c5exp(j5ωt)+c7exp(j7ωt)}
Świetnie są przestawione kolejne harmoniczne o malejących amplitudach i zwiększających pulsacjach 1ωt, 3ωt, 5ωt i 7ωt. Są to sumy wektorowe i sumy sinusoid. Obie dają oczywiście ten sam wynik czyli funkcję czasu f(t) zbliżoną do fali prostokątnej. 

Rozdział 3.5  Zespolony szereg Fouriera-wzór ogólny bez części rzeczywistej
A teraz najważniejsze czyli drugie tadam!!!
1. Jeżeli weźmiesz dowolną funkcję okresową f(t) o okresie T
2. Obliczysz pulsację podstawową ω=2π/T
3. Obliczysz współczynniki a0,a1,b1,a2,b2,…an,bn…  a następnie współczynniki zespolone
...c(-n)…c(-3),c(-2),c(-1),c0,  c1,c2,c3…cn… wg. wzoru Rys. 3-18
to
otrzymasz wzór zespolony szereg Fouriera–>Rys.3-19
Uwaga dla powyższych oznaczeń. np c(-3) to c z dolnym ujemnym indeksem -3. Nie umiem zapisać dolnego indeksu w Wordpresie.

Rys. 3-18a
Wzór na zespolone współczynniki c zespolonego szeregu Fouriera “bez części rzeczywistej”
Rys. 3-18b
Ten sam wzór na c(n) po uwzględnieniu wzoru Eulera exp(jωt)=cos(ωt)+jsin(ωt)
W porównaniu do wzoru Rys. 3-11
1. c0 czyli współczynnik składowej stałej jest identyczny
2. Pozostałe współczynniki c to liczby zespolone i połówki z Rys. 3-11 (Bo an i bn to połówki an i bn z Rys. 3-11)
3. Pary c(n) i c(-n) są liczbami sprzężonymi. Czyli ich suma c(n)+c(-n)=2a(n) jest liczbą rzeczywistą.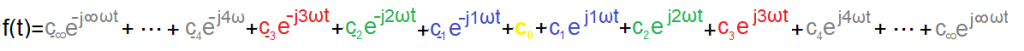

Rys. 3-19
Wzór na zespolony szereg Fouriera 
Pojawiły się pulsacje ujemne i współczynniki z  ujemnymi indeksami. Jest ich teraz 2 razy więcej z 2 razy mniejszymi modułami, ale w sumie dają tą samą rzeczywistą funkcję f(t)!

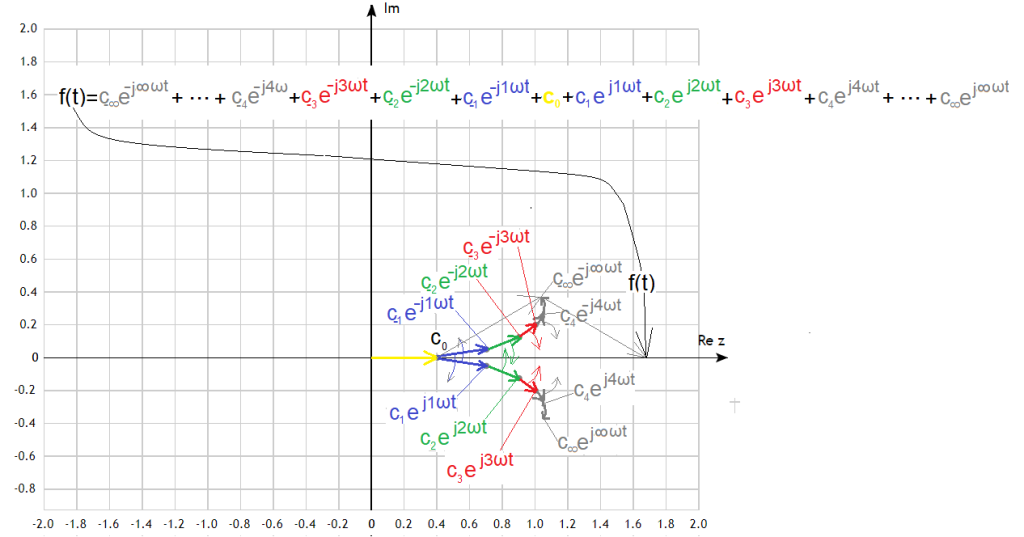
Rys. 3-20
zespolony szereg Fouriera jako suma wirujących przeciwnie wektorów
Ściślej “Suma wirujących przeciwnie wektorów+ składowa stała c0“
Uzasadnienie jest bardzo proste:
Każda para wirujących przeciwsobnie wektorów  to np:
c2exp(j2ωt)+c(-2)exp(-j2ωt)=a2cos(2ωt)+ b2sin(2ωt). Wyjaśniono to dokładnie w Rozdziale 3.3.2.
Czyli suma wszystkich par+ składowa stała c0=a0
da nam wzór Rys. 3-3
Czyli wzór Rys. 3-19
W eleganckiej i skondensowanej formie wygląda to tak:

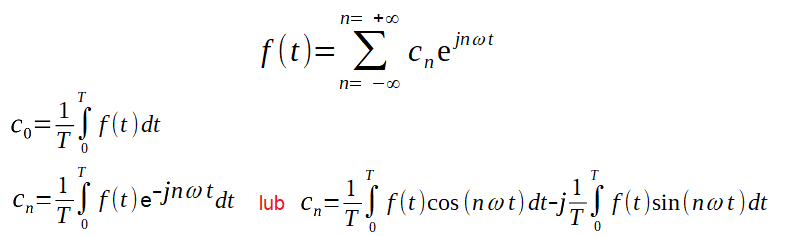
Rys. 3-21
zespolony szereg Fouriera
Wzór “bez części rzeczywistej” jest częściej spotykany niż równoważna wersja z “częścią rzeczywistą”.
Dlatego jest to po prostu wzór na zespolony szereg Fouriera.
Przy okazji dowiedziałeś się, że istnieje coś takiego jak częstotliwość/pulsacja dodatnia i ujemna. Dodatnią mają mają sinusoidy których wektory wirują przeciwnie do wskazówek zegara, ujemną-zgodnie. Kiedyś mnie to intrygowało. Można sobie jakoś wyobrazić, że częstotliwość zerową ma prąd stały. Ale ujemną? Coś bardziej “stałego niż stała”? I jak tu żyć? Teraz już wiem.