Szeregi Fouriera klasycznie
Rozdział 1 Wstęp
Rozdział 1.1 Wstęp
Jest to także wstęp do następnych kursów “Transformata Fouriera” i “Transformata Laplace’a”. Ten ostatni pojawi się w przyszłości.
Rozdział 1.2 Każdą funkcję czasu f(t) można rozłożyć na sinusoidy!
Może nie każdą*, ale nie bądźmy drobiazgowi. Najłatwiej gdy mamy do czynienia z funkcjami okresowymi f(t) trwającymi od minus do plus nieskończoności tak jak na Rys. 1-2.c. Tu jest właśnie robota dla Szeregu Fouriera.
A gdy funkcja przebiega w skończonym czasie, np. pojedynczy impuls prostokątny? Albo w nieskończonym czasie ale energia impulsu jest skończona, np napięcie rozładowania układu RC. Tym zajmuje się Transformata Fouriera której kurs też znajdziesz na stronie głównej.
A gdy funkcja przebiega w nieskończonym czasie i ma nieskończoną energię np. skok jednostkowy lub funkcja kwadratowa? Tu jest robota dla Transformaty Laplace’a.
Wniosek
Szereg Fouriera, Transformata Fouriera lub Transformata Laplace’a rozkładają prawie każdą* funkcję f(t) na sumę sinusoid o różnych częstotliwościach, amplitudach i przesunięciach fazowych!
*“prawie każdą funkcję”- oprócz np. tego typu dziwolągów.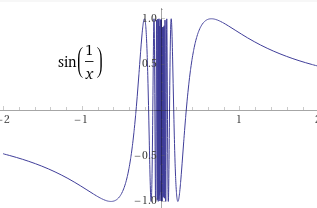
Rys. 1-1
Funkcja która nie podlega Szeregowi lub Transformacie Fouriera.
Na szczęście takie funkcje rzadko związane są z realnymi zjawiskami fizycznymi.
Rozdział 1.3 Trygonometryczny szereg Fouriera
Funkcję okresową f(t) można przybliżyć Szeregiem Fouriera.
Tu f(t) jest akurat funkcją czasu t, ale równie dobrze może być też funkcją położenia x czyli f(x).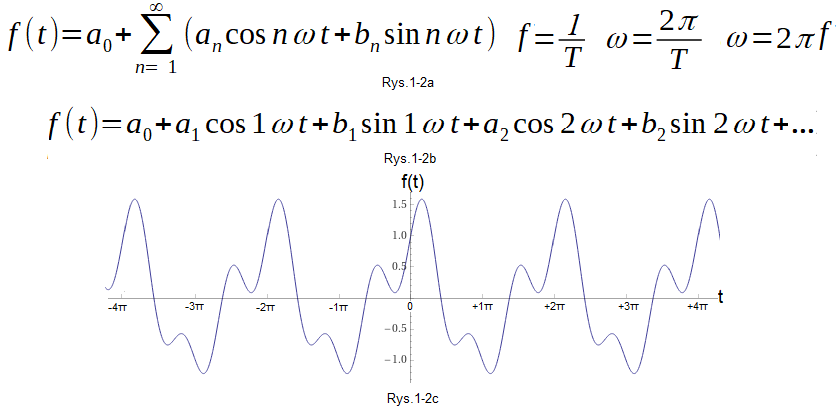
Rys.1-2
Trygonometryczny rozkład funkcji okresowej f(t) na Szereg Fouriera.
Uwaga:
Do opisów prądów zmiennych używa się częstotliwości f jako odwrotności okresu T lub tzw. pulsacji, inaczej prędkości kątowej ω. Częstotliwość f używana jest przez zwykłych zjadaczy chleba np. f=50 Hz, natomiast pulsacja ω przeznaczona jest dla elektryków. Wtedy wzory są trochę krótsze, bo zamiast 2πf mamy tylko ω.
Rys. 1-2a Wzór z użyciem znaku sumy-sigma
Rys. 1-2b Wzór bez użycia tego znaku, który jest chyba bardziej przejrzysty. Lepiej tu widać pulsację ω pierwszej harmonicznej.
Pulsacje kolejnych harmonicznych to ich wielokrotności. Współczynniki a1,b1,a2,b2… to amplitudy kolejnych sinusoid/cosinusoid.
Są to stałe np. a1=1 ,b1=-0.5,a2=0 ,b2=1.25,a3=0.1, … które omówimy w Rozdziale 2.
Rys. 1-2c Przykład funkcji okresowej f(t) o okresie T=2π sek odpowiadającym pulsacji ω=1/sek.
Powyższe wzory są dokładne najczęściej dla n=∞. Wartość n może być też skończona np. n=3 na Rys. 2-3 w Rozdziale 2.
Rozdział 1.4 Zespolony szereg Fouriera
Jest to po prostu inaczej zapisany Trygonometryczny szereg Fouriera.
W pierwszej chwili mniej zrozumiały, no bo jakieś liczby zespolone zamiast poczciwych rzeczywistych. Ale wiele wiele rzeczy liczy się łatwiej. Mało tego, jest bardziej intuicyjny! Zwłaszcza po obejrzeniu animacji. Zauważysz np. analogię do Układu Słonecznego, w którym Ziemia krąży wokół Słońca, Księżyc wokół Ziemi itd… Więcej na ten temat w Rozdziale 3.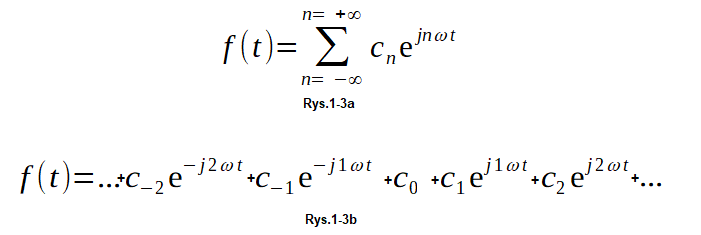
Rys. 1-3
Zespolony rozkład funkcji okresowej f(t) na Szereg Fouriera.
Rys. 1-3a Wzór z użyciem znaku sumy-sigma
Rys. 1-3b Wzór bez użycia tego znaku. Chyba bardziej przejrzysty.
Wzory są ewidentnie prostsze niż na Rys. 1-2. Niestety, użyte współczynniki cn są liczbami zespolonymi. W celu ich przypomnienia kurs Liczby zespolone na stronie głównej.
Zauważ, że po prawej równań jest dość skomplikowana suma liczb zespolonych, której wynikiem jest jednak funkcja rzeczywista f(t)! Składowe urojone nawzajem się skompensowały!![]()
Rys. 1-4
Współczynniki Szeregu Fouriera jako liczby zespolone.
Rozdział 1.5 Do czego to wszystko jest potrzebne?
Chociaż Szeregi Fouriera pojawiły się ponad 200 lat temu, to znalazły zastosowanie także w naszych czasach. A tzw. Szybka Transformata Fouriera, która jest tylko cyfrowym algorytmem obliczania transformaty Fouriera została opublikowana dopiero w 1965 r przez Cooleya i Tuckeya.
Do czego to wszystko jest potrzebne? Okazuje się, że trudno znaleźć dziedzinę w której nie byłoby szeregu lub transformaty Fouriera
Przykład z akustyki. Słowo “hello” zarejestrowano mikrofonem jako funkcja czasu f(t).
Autorem jest Erik Cheever. Przy okazji serdecznie polecam jego artykuł https://lpsa.swarthmore.edu/Fourier/Series/WhyFS.html .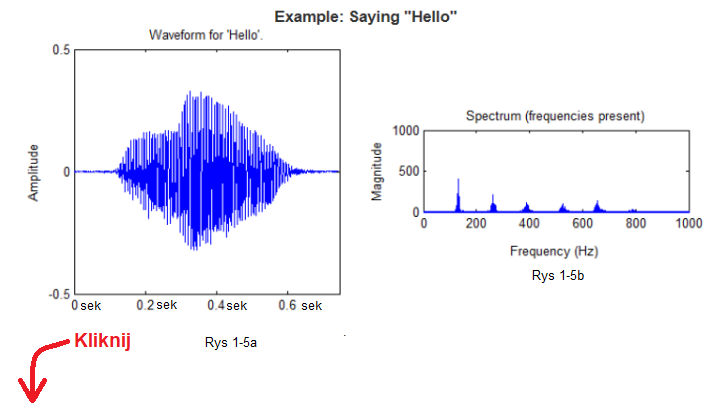
Kliknij przycisk rejestratora dźwięku. Usłyszysz niezbyt głośne “Hello”.
Rys. 1-5
Słowo “Hello” zapisane jako:
Rys.1-5a funkcja czasu f(t)
Dla przeciętnego zjadacza chleba zjawisko fizyczne (tu słowo “hello”) kojarzy się z funkcją czasu tak jak na Rys.1-5a. Funkcja f(t) zaczyna się dla t=0.1 sek i kończy w t=0.6 sek. Jest bardzo zagmatwana w porównaniu do np. funkcji kwadratowej Jak ją analizować?
Rys.1-5b widmo częstotliwościowe F(ω)
Funkcja f(t) słowa “hello” jako suma konkretnych sinusoid z których każda ma swoją amplitudę, pulsację ω (na Rys.1-5b częstotliwość f) i fazę φ. Wykres pokazuje tylko same amplitudy, tak że nie zawiera pełnej informacji o “hello” ale jest ewidentnie prostszy niż Rys.1-5a. Pierwszą korzyść z podejścia do zjawiska jako rozkładu częstotliwości czyli widma F(ω) zobaczysz w następnym nagraniu. Usłyszysz to samo “hello” ale z irytującym zakłóceniem. 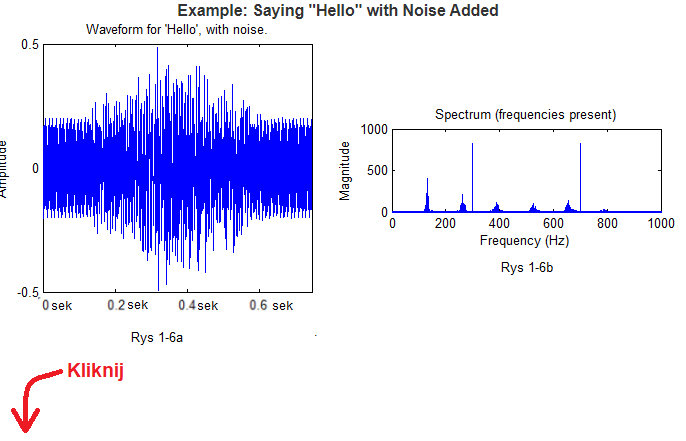
Rys. 1-6
Słowo “Hello” zapisane jako:
Rys.1-6a funkcja czasu f(t)
Zauważ, że chociaż zakłócenie-ciągły ton, jest niezbyt skomplikowane to, wykres czasowy sporo się zmienił. Gdzie w tym kłębowisku żmij szukać zakłócenia?
Rys.1-6b widmo częstotliwościowe F(ω)
Widmo częstotliwościowe F(ω) niewiele się zmieniło w porównaniu do Rys.1-5a. Pojawiły się tylko 2 dodatkowe prążki sinusoid w okolicach 300Hz i 700Hz. Wystarczy tylko je wyciąć i otrzymamy czyste “Hello” jak poprzednio. To wycięcie jest precyzyjne jeśli zastosujemy algorytmy cyfrowe. Kiedyś stosowano filtry analogowe z cewkami i pojemnościami, które przy okazji wycinały częstotliwości oryginalne.
Mam nadzieję, że widzisz korzyść z widmowego podejścia do funkcji czasu.
Rozdział 1.6 Inne dziedziny z szeregiem Fouriera lub Transformatą
Cyfrowe przetwarzanie obrazów
Widziałeś chyba film w którym Marszałek Piłsudski jest jak żywy. Tak jakby zrobiono go wczoraj z dobrej komórki. A to wszystko dzięki Transformacie Fouriera. O co chodzi? Każdy obraz można rozłożyć na sinusoidy o znanych parametrach. Wystarczy je tylko zapamiętać i odtworzyć jako obraz w dowolnym momencie. Zwykle zajmie to mniej miejsca niż zapamiętanie każdego piksela obrazu. Jest to przykład w którym sinusoidy dotyczą przesunięcia x a nie czasu t. A najważniejsze to łatwiej usunąć zakłócenia-niepotrzebne dodatkowe sinusoidy z niedoskonałego oryginału z przed 100 lat. Podobnie jak z dźwiękiem na Rys.1-6.
Diagnostyka maszyn
Turbogenerator musi być idealnie wyważony. Przecież to są tony szybko obracającej się masy. Idealna maszyna daje odpowiednie widmo F(ω) dla częstotliwości zmieniającej się w zakresie od 0 do odpowiadającej maksymalnym obrotom. A gdyby do wału dostał się jakiś opiłek? Ucho ludzkie może tego nie wychwycić ale na widmie pojawi się wyraźny prążek. Teraz znalezienie tego opiłka to tylko kwestia dokładnego obejrzenia wału.
Trzęsienia ziemi
Na szczęście nie dotyczy to wszystkich tylko niektórych np. mieszkańców Kalifornii. Wykres czasowy tzw. sejsmograf można dzięki Panu Fourierowi rozbić na poszczególne harmoniczne. Po iluś tam latach okaże się, że pewne częstotliwości przeważają. A to już jest ważna informacja dla architektów. Budynki same sobą muszą je tłumić! Na pewnych wysokościach są odpowiednie duże bujające się masy, które w sumie z całą resztą budynku zmniejszają jego amplitudy wahań. Dlaczego? Bo bujają się w przeciwfazie do reszty budynku.
Automatyka
Układy regulacji, bez i ze sprzężeniem zwrotnym opisane są równaniami różniczkowymi. Na szczęście, przy pewnych uproszczeniach są to równania różniczkowe liniowe. Równania będą łatwiejsze gdy jego rozwiązanie, czyli funkcję f(t) rozłożymy na składowe sinusoidalne. A to nic innego jak Szereg , Transformata Fouriera lub Transformata Laplace’a. Dlaczego łatwiejsze. Bo pochodną sinusa jest cosinus a cosinusa sinus (z minusem co prawda). Nie będę wnikał w szczegóły ale takie równania można zamienić na równania kwadratowe lub wyższych stopni. Teraz możemy je rozwiązywać i analizować korzystając ze “zwykłej” algebry.
Medycyna
Nie raz leżałeś u lekarza na kozetce podłączony kabelkami do monitorów.
Dla Kardiologa wykres na monitorze jest elektrokardiogramem
Dla Neurologa jest elektroencefalogramem.
Na ich podstawie doświadczony lekarz wie mniej więcej co Ci dolega. Doświadczenie nabywa z praktyką. Zwłaszcza, że wykresy niewiele się różnią. I tu jest pole dla Transformaty Fouriera, która funkcję f(t) rozbije na poszczególne sinusoidy, uproszczając widma częstotliwości. Widma dla różnych chorób są różne. Tu przyda się wspomniana wcześnie Szybka Transformata Fouriera–FFT.
Przykładem na to jak neurolodzy głęboko wchodzą w Transformatę Fouriera jest youtube .Kliknij
