Scilab

Rozdział 7.2 Ładowanie kondensatora jako przykład najprostszego równania różniczkowego
Czyli równania różniczkowego  I rzędu tzn. najwyższą pochodną w tym równaniu jest pierwsza pochodna dy/dt inaczej y'(t).

Rys. 7-1
Ładowanie kondensatora jako przykład równania różniczkowego zwyczajnego pierwszego rzędu.
Rys.7-1a
Układ RC
Każdy elektryk/elektronik zaczyna od tego układu.
Rys.7-1b
Równanie różniczkowe opisujące proces ładowania kondensatora.
Stan początkowy czyli dla to=0sek napięcie kondensatora y(to)=0V
Pochodna y(t) czyli dy/dt=(1/T)x(t)-(1/T)y(t) jest prędkością ładowania kondensatora C. Jest największa dla to=0sek, bo kondensator C jest nienaładowany (y(t)=0) i różnica (1/T)*x(t)-(1/T)*y(t) jest największa. Potem kondensator się trochę naładuje i ta różnica zmniejszy się. Czyli prędkość ładowania, inaczej nachylenie dy/dt też się zmniejszy. Aż dojdziemy do stanu ustalonego gdy dy/dt=0. Inaczej, y(t) stanie się linią poziomą.
Rys.7-1c
Proces ładowania kondensatora jako rozwiązanie równania różniczkowego z Rys.7-1b.
Nie wnikamy jak, ale podstaw t=0 i t=10sek do równania na rysunku i zobacz, że się zgadza. Zauważ, że im większe T (duże R i C!), tym układ jest bardziej “leniwy”. Z elektrotechniki wynika, że T=RC. Z kursu Podstaw Automatyki tego portalu dowiesz się, że układ RC jest przykładem tzw. członu inercyjnego K/(1+sT) o wzmocnieniu K i stałej czasowej T.
Rozdział 7.3 Uogólnienie równania różniczkowego I rzędu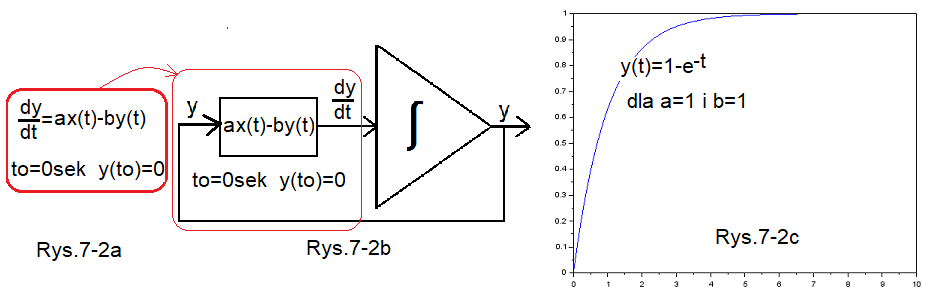

Rys. 7-2
Bardziej uogólnione równanie różniczkowe
Rys. 7-2a
Uogólnienie równania Rys.7-1a 
Jest to przykład równania różniczkowego liniowego I rzędu o stanie początkowym to=0, y(to)=0.
Parametry a i b to dowolne stałe np. a=1 b=1 
Uwaga: 
Jestem automatykiem i dlatego równania różniczkowe kojarzą mi się najczęściej z funkcjami czasu y(t), rzadziej z funkcją przesunięcia y(x). Dla matematyka nie ma to żadnego znaczenia.
Rys. 7-2b
Schemat z układem całkującym dla rozwiązania równania z Rys.7-2a.
Kiedyś w latach 1950…1960 komputery nazywały się maszynami matematycznymi analogowymi i cyfrowymi. Maszyny cyfrowe to po prostu komputery, a analogowe to zapomniane trochę w dzisiejszych czasach układy z członami całkującymi jak powyżej. W prostokącie jest schemat wykonujący operację matematyczną ax(t)-by(t), a ogólnie f(t,y). Za układem całkującym jest napięcie y(t). W stanie początkowym to=0 często ma wartość y(to)=0. Tak jak dla każdego układu całkującego” za” jest y(t), a “przed” pochodna dy/dt. Układ zacznie rozwiązywać równanie różniczkowe począwszy od to=0 i y(to)=0, dając przebieg taki jak na Rys. 7-2c. 
Rys. 7-2c
Rozwiązanie równania różniczkowego z Rys.7-2a przez układ z Rys.7-2b.
 a=1, b=1 y(to)=0 i gdy x(t)=1(t) jest skokiem jednostkowym.
Rozwiązaniem analitycznym, czyli “ołówkiem przez matematyka” jest y(t)=1-exp(-t).
Jak nie wierzysz, to podstaw y(t)=1-exp(-t) do równania różniczkowego  y'(t)=1(t)-exp(-t).
Rozdział 7.4 Najbardziej ogólne równanie różniczkowe I rzędu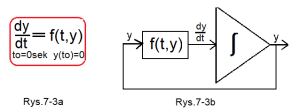

Rys.7-3a
Najbardziej ogólne równanie różniczkowe I rzędu
Po prawej stronie dy/dt jest dowolne wyrażenie f(t,y), gdzie t jest czasem, a y jest funkcją czasu y(t).
W prostych przypadkach może być np. f(t,y)=y(t).
Rys.7-3b
Schemat z układem całkującym do rozwiązywania równania z Rys.7-3a.
Rozdział 7.5 Przykłady równań różniczkowych I rzędu
Wyrażenie f(t,y) w równaniu Rys.7-3a jest mało mówiące. Przyda się kilka konkretnych przykładów.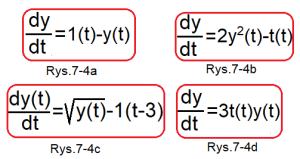

Rys.7-4a
Równanie różniczkowe liniowe I rzędu
Sygnał x(t)=1(t) jest skokiem jednostkowym, tzn. 1(t)=0 dla t<0 i 1(t)=1 dla  t>0.
Tu i na pozostałych rysunkach nie pokazałem stanu początkowego np. to=0 i y(to)=0.
Rys.7-4b
Równanie różniczkowe  nieliniowe, bo zawiera 2y²(t).
Funkcja t(t) jest tzw. “piłą”—>t(t)=0 dla t<0 i t(t)=t dla t>0.
Rys.7-4c
Równanie różniczkowe nieliniowe, bo y(t) jest “pod pierwiastkiem”. Sygnał 1(t-3) to skok opóźniony o 3sek.
Rys.7-4d
Inny przykład równania różniczkowego nieliniowego.
Dodam jeszcze, że sygnał wejściowy x(t) może być nieliniowy, np. x(t)=t²(t) lub skoki 1(t), 1(t-3), chociaż np. całe dy/dt=3y(t)+t²(t) jest równaniem różniczkowym liniowym!
Rozdział 7.6 Jak model z Rys.7-3b rozwiązuje równanie różniczkowe
Przeanalizujemy układ rozwiązujący równanie różniczkowe z Rys.7-3b. Tam czas działał ciągle. Skwantujemy go tzn. zbadamy jego stany w czasie to do t4  z odstępem co czas Δt. Wiemy, że przybliżoną wartością pochodnej dy/dt jest tzw. iloraz różnicowy Δy/Δt. Czyli dy/dt≈Δy/Δt.
Okaże się, że znając stan  początkowy y(to) obliczymy
Δyo/Δt=f(to,yo) –>Δyo=f(to,yo)Δt
Czyli obliczymy y1=y0+Δyo=y0+f(to,yo)Δt
Analogicznie znając y1 obliczymy y2 (bo obliczymy Δy1/Δt1=f(t1,y1)    itd…
Czyli
y2=y1+f(t1,y1)Δt
y3=y2+f(t2,y2)Δt
y4=y3+f(t3,y3)Δt
Zakładamy, że przyrosty czasu Δt są równe–>Δt0=Δt2=Δt3=Δt4=…=Δt.
W ten sposób obliczymy wszystkie wartości y(ti)  od czasu początkowego to=0 do końcowego tu tk=10sek. Czyli znając stan początkowy y(to)=yo rozwiążemy równanie różniczkowe I rzędu dy/dt=f(t,y). Jest to oczywiście rozwiązanie przybliżone, tym dokładniejsze im mniejsze jest Δt.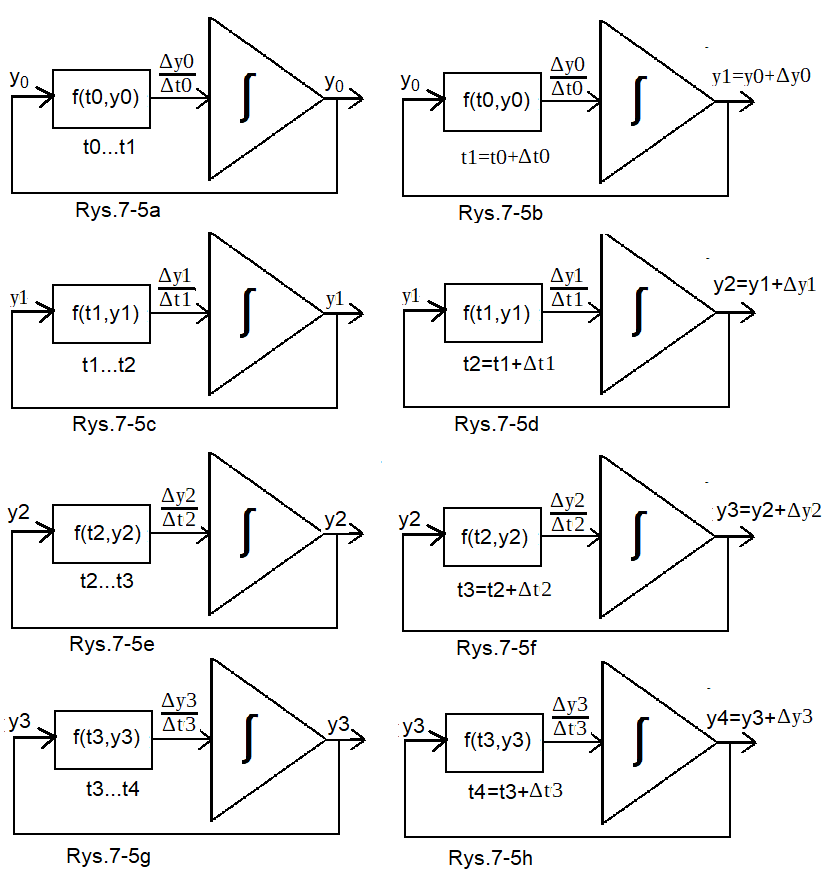

Rys. 7-5
Stan modelu z Rys.7-3a w czasie od to do t4
Rys. 7-5a
Na wyjściu członu całkującego jest stan początkowy y(to)=y0. Natychmiast zostanie obliczona “pseudopochodna“, albo inaczej iloraz różnicowy Δyo/Δto=f(t0,y0) jako pewna wartość stała. W czasie Δto od to do t1 człon całkujący “nacałkuje”  z prędkością Δyo/Δto od wartości y0 do y0+Δyo. 
Rys. 7-5b
Jest to fotografia Rys.7-5a w jego końcowej chwili t1. Czyli y1=y0+Δy0. Jest to jednocześnie stan początkowy z Rys. 7-5c.
Rys. 7-5c
Chwila początkowa t1 jest taka sama jak na Rys. 7-5b. Jest to właściwie ten sam stan, z tym że w czasie t1 jest obliczany nowy iloraz różnicowy Δy1/Δt1=f(t1,y1) jako nowa ‘pseudopochodna”. W czasie Δt1 od t1 do t2 człon całkujący “nacałkuje”  z prędkością Δy1/Δt1 od wartości y1 do y1+Δy1. 
Rys. 7-5d
Jest to fotografia Rys.7-5c w jego końcowej chwili t2. Czyli y2=y1+Δy1. Jest to jednocześnie stan początkowy z Rys. 7-5e.
Rys. 7-5e
Opis podobny do Rys. 7-5c.
Rys. 7-5f
Opis podobny do Rys. 7-5d.
Rys. 7-5g
Opis podobny do Rys. 7-5e.
Rys. 7-5f
Opis podobny do Rys. 7-5d.
Następne stany dla t5, t6, …tk  też obliczane są w podobny, tzn. rekurencyjny sposób.
Rozdział 7.7 Jak rozwiązać konkretne równanie np. dy/dt=y(t)-1(t)
Czyli rozwiązanie dla równania z Rys.7-4a jako szczególnego przypadku z Rys. 7-2a, dla a=1, b=1 i x(t)=1(t). Rozwiązaniem  tego równania jest Rys. 7-2c.
Czy przybliżone rozwiązanie bazujące na Rozdziałe 7.6 to potwierdzi?

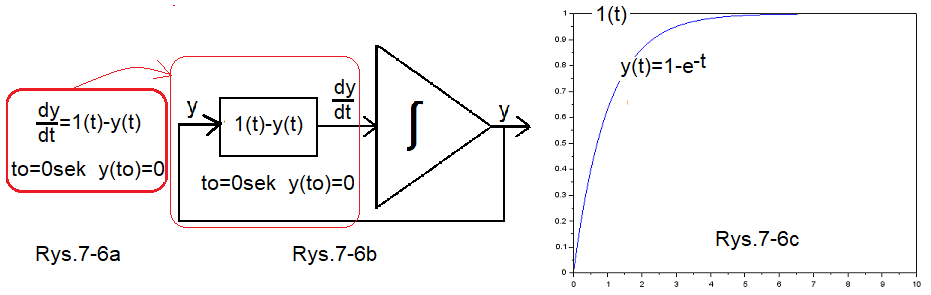
Układ całkujący jako maszynka do rozwiązania równania dy/dt=1(t)-y(t)
Rys.7-6a
Równanie różniczkowe z zerowymi warunkami początkowymi
Rys.7-6b
Maszynka rozwiązująca równanie dy/dt=1(t)-y(t)
Rys.7-6c
y(t)=1-exp(-t) jako dokładne rozwiązanie (“ołówkiem”) równania dy/dt=1(t)-y(t)
Proponuję podstawić y(t) do równania różniczkowego i sprawdzić. Pamiętaj, że [exp(-t)]’=-exp(-t)
A teraz rozwiążemy to równanie numerycznie, zakładając, że  dy/dt≈ Δy/Δt. Tym dokładniej im mniejszy jest przyrost czasu Δt.

Rys.7-7
Numeryczne rozwiązania równania różniczkowego y'(t)=1(t)-y(t)
Rys.7-7a
Dokładne równanie różniczkowe–> y'(t)=1(t)-y(t)
Równanie różnicowe jako przybliżone równanie różniczkowe–>Δy/Δt=1(t)-y(t)
Rys.7-7b
Jak z równania różnicowego otrzymano  równanie rekurencyjne y(n+1)=y(n)(1-Δt)+Δt?
Mój wnuk zdawał wczoraj egzamin 8-klasisty. Gdyby iloraz różnicowy traktował jak zwykły iloraz, nie mający nic wspólnego z rachunkiem różniczkowym, doszedłby do równania w czerwonej ramce. Zauważ, że przy danym przyroście Δt współczynnik (1-Δt) jest stały, co bardzo ułatwia obliczenia, np. dla Δt=0.1  (1-Δt)=0.9.
Rys. 7-7c
Wartości y(2),y(3),y(4)…y(n+1) obliczone na podstawie równania Rys. 7-7b i znanych wartości y(1) i Δt. 
y(1)=0 jako znana wartość początkowa równania. 
y(2)=Δt zawsze
y(3)=y(2)*(1-Δt)+Δt od tego zaczyna się rekurencja. 
Zauważ, że dla danego Δt, np. Δt=0.1sek–>1-0.1=0.9, ta rekurencja jest bardzo prosta y(n)=y(n-1)*0.9+0.9
Rys. 7-7d
Kolejne y(n) gdy Δt=1sek
Sprawdź dla kilku n. Niezbyt dokładnie, bo Δt=1sek w porównaniu do zakresu t=10sek jest duże! Gdybyśmy zwiększyli np. na Δt=2sek byłoby jeszcze gorzej! Sprawdź. Zgadza się z intuicją. Im mniejsze Δt tym bardziej iloraz różnicowy Δy/Δt jest podobny do pochodnej dy/dt!
Rys. 7-7e
Kolejne y(n) gdy Δt=0.5sek
Rys. 7-7f
Kolejne y(n) gdy Δt=0.25sek
Rys. 7-7g
Kolejne y(n) gdy Δt=0.1sek
Wnioski
Spodziewamy się, że zmniejszając Δt odpowiedź y(n) zbliża się do rozwiązania idealnego Rys. 7-6c.  
Rozdział 7.8 Rozwiązanie powyższego równania przy pomocy Scilaba.
Rozdział 7.8.1 Analiza pierwszej części programu
Na razie przeanalizujemy pierwszy kawałek programu w którym stworzymy i sprawdzimy przyrost Δt ilorazu różnicowego oraz wektory t i skok.
Program 7-1

clc;clear;clf
jtmax=10
Czas_eksperymentu=10
Δt=Czas_eksperymentu/jtmax
disp('Δt=',Δt)
t=0:1:jtmax
disp('t=',t)
skok=t
for j=1:jtmax+1
   skok(j)=1
end
disp('skok=',skok)

Przypomnę co robią poszczególne instrukcje
clc;clear;clf 
Standardowe czyszczenie ekranu konsoli, zmiennych i wykresów
jtmax=10
Przewidziana liczba obliczeń tu 10, ale tak naprawdę to będzie jtmax+1 czyli 11. 
Zwykle jtmax jest większe np. 100, 1000…
Czas_eksperymentu=10 
Nasze równanie różniczkowe obejmuje czas t=10sek.
Inaczej, dziedziną równania różniczkowego jest czas t=10sek.
Δt=Czas_eksperymentu/jtmax
Δt przyrost czasu obliczony dla ilorazu różnicowego.
disp(‘Δt=’,Δt) 
Wyświetlenie Δt 
t=0:1:jtmax
Wektor t z dyskretnymi czasami t=[0,1…jtmax] na którym będą określone wektory 
disp(‘t=’,t) 
Wyświetlenie wektora t 
skok=t
Definicja nowego wektora skok. Na razie skok taki sam jak t
for j=1:jtmax+1
  skok(j)=1
end
Zamiana wektora skok z “czasowego” na skokowy (z “jedynkami”). Tu może zastanawiać dlaczego jest
for j=1:jtmax+1 a nie for j=0:jtmax? Dlatego, że wektory t i skok nie zaczynają się od t(0), skok(0), ale od t(1), skok(1). Bo taka jest uroda wszystkich wektorów w Scilabie.
disp(‘skok=’,skok)
Wyświetlenie wektora skok
Na animacji Rys. 4-2 w rozdz. 4 pokazałem jak wykonać program w Scilabie i nie powinno być żadnych problemów z wykonaniem powyższego. 
Wykonaj ten program. Otrzymasz coś takiego.
Δt=
1.// Ponieważ czas eksperymentu t=10sek i jtmax=10 to
Δt=1sek dość duże. Zwykle Δt dużo mniejsze.
0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
“skok=”
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
Wszystko tzn. Δt i wektory są takie jakie przewidzieliśmy.
Rozdział 7.8.2 Analiza całego programu
Skoro mamy już obliczone na podstawie jtmax
-Δt – przyrost czasu
-t wektor czasu z jednostkami czasu od 0 do 10sek
-skok wektor z jtmax jednostkami skoku jednostkowego
to możemy porównać na wykresie rozwiązanie różnicowe y(j) z Rys. 7-7d…7-7g z rozwiązaniem idealnym z Rys. 7-6c. Spodziewamy się, że wraz ze zmniejszającym się Δt rozwiązanie różnicowe będzie zbliżało się do idealnego.
Program 7-2

clc;clear;clf
jtmax=10
Czas_eksperymentu=10
Δt=Czas_eksperymentu/jtmax
t=0:1:jtmax
skok=t
for j=1:jtmax+1
   skok(j)=1
end//do tego miejsca opis w rozdz. 7.8.1
ideal=skok
for j=1:jtmax+1//patrz wyjaśnienie pierwsze 
ideal(j)=(1-exp((1-j)*Δt))
end
real=skok
real(1)=0
for j=2:jtmax+1 //patrz wyjaśnienie drugie i trzecie 
    real(j)=Δt+(1-Δt)*real(j-1)
end
plot(t,skok,'o')
plot(t,skok)
plot(t,ideal,'o')
plot(t,ideal)
plot(t,real,'o')
plot(t,real,'r')

Wyjaśnienie pierwsze gdy np. jtmax=10–>Δt=1sek
Czyli obliczamy przebieg idealny rozwiązania równania z Rys.7-6c dla Δt=1sek
j=1–>ideal(1)=y(1)=1-exp(1-1)*1=0
j=2–>ideal(2)=y(2)=1-exp(1-2)*1=0.6321…
j=3–>ideal(3)=y(3)=1-exp(1-3)*1=0.8646…
j=4–>ideal(4)=y(4)=1-exp(1-4)*1=0.9502…
…
j=10–>ideal(10)=y(10)=1-exp(1-10)*1=0.9998…
Widzimy, że obliczenia idealnego rozwiązania pokrywają się z Rys.7-1c

Wyjaśnienie drugie gdy jtmax=10–>Δt=1sek
Czyli obliczamy przebieg przybliżonego rozwiązania równania z Rys.7-7d dla Δt=1sek
j=1–>real(1)=y(1)=0
j=2–>real(2)=y(2)=Δt=1
j=3–>real(3)=y(3)=y(2)*(1-1)+Δt=Δt=1 
j=4–>real(4)=y(4)=y(3)*(1-1)+Δt=Δt=1
…
j=11–>real(11)=y(11)=y(10)*(1-1)+Δt=Δt=1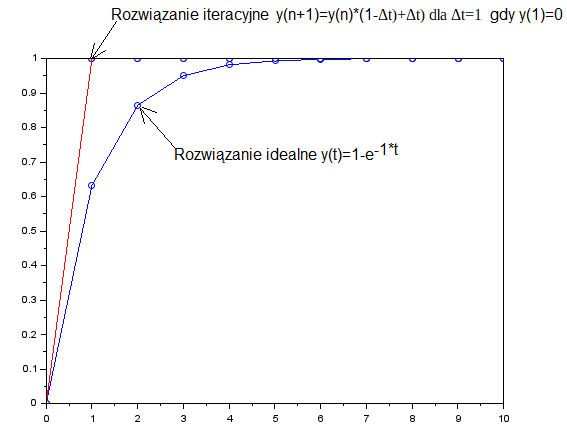

Rys.7-8
Wykres rozwiązania idealnego i iteracyjnego dla Δt=1sek
Skok jednostkowy 1(t) idealnie pokrywa się z “górą” rysunku. Przybliżenie iteracyjne to górne kropki a dolne to idealne rozwiązanie. Lepiej widać różnicę między rozwiązaniem idealnym i iteracyjnym niż na “liczbach” w wyjaśnieniu pierwszym i drugim. Jeszcze jedno. Na wykresie kółka zostały połączone odcinkami prostymi, dzięki czemu wykres upodobnił się do prawdziwego.
Dziwne, przebieg przybliżony jest prawie prostokątny. Ale jest to pierwsze i bardzo zgrubne przybliżenie gdy Δt=1sek. Ale gdybym wynajął dobrego adwokata, to udowodniłby, że przebieg wykładniczy to prawie skok!
Na pewno będzie lepiej gdy Δt=0.1. Sprawdźmy

Wyjaśnienie trzecie gdy jtmax=100–>Δt=0.1sek
Czyli obliczamy przebieg rzeczywistego rozwiązania równania z Rys.7-7g dla Δt=0.1sek
j=1–>real(1)=y(1)=0 
j=2–>real(2)=y(2)=Δt=0.1–>=0.9
j=3–>real(3)=y(3)=y(2)*(1-01)=y(2)*0.9=0.1 9
j=4–>real(4)=y(4)=y(3)*0.9=0.271
j=5—>real(5)=y(5)=y(4)*0.9+Δt=Δt=0.3419
…
j=101–>real(101)=y(101)=y(100)*0.9+Δt=Δt=0.9999734…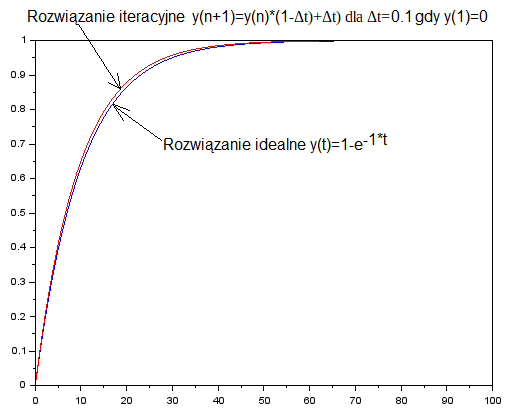

Rys.7-9
Wykres rozwiązania idealnego i iteracyjnego dla Δt=0.1sek
Wykres jest bardziej przejrzysty, bo zrezygnowałem z kropek. Byłoby ich 101 i czyniłby wykres mniej przejrzysty. Ewidentnie widać, że wykres iteracyjny zbliżył się do idealnego. To sprawdźmy dla jtmax=250, gdy Δt=0.04sek. Na pewno będzie lepiej, ale o ile?. Zrezygnujemy z cześci obliczeniowej, damy tylko wykres.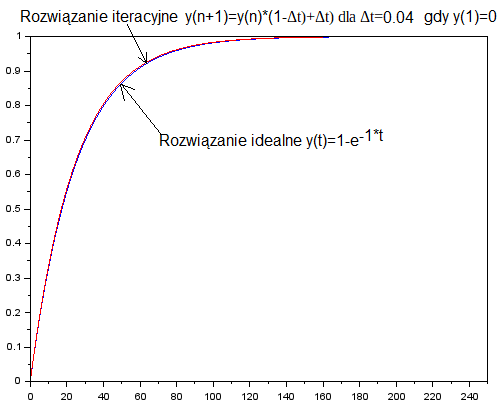

Rys.7-10
Wykres rozwiązania idealnego i iteracyjnego dla Δt=0.04sek
Tak jak się spodziewaliśmy, wykres idealny prawie pokrywa się z iteracyjnym. Pokrywa się także z intuicją. Im mniejsze Δt, tym większa dokładność rozwiązania równania różniczkowego. Czy aby tak do końca? Są pewne granice zmniejszania Δt. Po pierwsze sam komputer oblicza ze skończoną dokładnością. Po drugie. Im  mniejsze Δt, tym większe jtmax, tym więcej iteracji. A w czasie iteracji błędy się kumulują.  Może na tym skończymy rozważania o dokładności modelowania matematycznego. Ale do jednego podstawowego wniosku doszliśmy. Istnieje pewna optymalne Δt. Nie za duże, nie za małe.