Podstawy automatyki
Rozdz. 28 Dobór nastaw regulatorów
Rozdział 28.1 Wstęp
W rozdziałach 23..27 omawialiśmy zasadę działania regulatorów P, PD, I, PI i PID. Sądzę, że dobierając ręcznie metodą prób i błędów nastawy Kp, Ti i Td dobrze zrozumiałeś ich role. Przy okazji poznałeś pierwszą metodę doboru nastaw. Metoda prób i błędów, używaną także w innych dziedzinach dalekich od automatyki.
Przykład
Jesteś bardzo ostrożny jadąc pierwszy raz na nartach. Skręcasz dużymi zakosami, długo hamujesz, przewracasz się. Podobny jesteś do obiektu z regulatorem PID z bardzo ostrożnymi nastawami. Małe Kp i Td, całkowania prawie nie ma czyli bardzo duże Ti. Ucząc się nabierasz doświadczenia, ruchy są coraz bardziej precyzyjne. A co to oznacza w języku automatyki? To,że poprawiasz nastawy swojego prywatnego regulatora Kp, Ti, Td zakodowanego w zwojach mózgowych. W końcu śmigasz slalomem między tyczkami. Twój regulator jest już prawie optymalny. Podejrzewam, że Radwańska, Wiliams czy inna Woźniacki, najlepsze tenisistki świata, mają nastawy swoich regulatorów bardzo zbliżone do siebie. Ale tylko mistrzyni ma trochę lepsze. Kończę z tą naiwną i mocno uproszczoną filozofią.
Na czym to stanęło? Że pierwszym podejściem do strojenia regulatorów (czyli dobierania Kp, Ti i Td) jest metoda prób i błędów–> inaczej metoda ręczna. Przejdźmy teraz do metod poważnych.
Przedstawię trochę staromodne metody wymyślone jeszcze w czasie II wojny światowej przez niejakiego Zieglera i Nicholsa:
– Metoda odpowiedzi skokowej
– Metoda cyklu granicznego
Każda jest przykładem innej szkoły. Pierwsza wymaga opisu matematycznego, czytaj transmitancji Go(s) obiektu. Druga tylko zbadania obiektu, a ściślej zmierzenia okresu drgań przy pewnym wzmocnieniu tzw. krytycznym. Jest więc mniej wybredna co do dokładnej znajomości obiektu.
Rozdział 28.2 Metoda odpowiedzi skokowej
Rozdział 28.2.1 Wstęp
Wymaga znajomości modelu matematycznego danego obiektu.
Model możemy uzyskać poprzez:
– dokładną analizę matematyczną poprzez znajomość procesów fizyko-chemicznych. Jest to oczywiście zadanie dla ambitnych.
– nie wnikamy w żadne termodynamiki, tylko badamy odpowiedź na skok jednostkowy. Zadanie mniej ambitne i łatwiejsze i dlatego ją omówimy.
Wystąpią w niej 4 etapy.
1-Badanie odpowiedzi obiektu na skok w układzie otwartym i wyznaczanie transmitancji przybliżonej Gp(s) jako inercji T i opóźnienia To
2-Wyznaczenie z odpowiednich tabel nastaw optymalnych Kp, Ti i Td
3-Sprawdzenie odpowiedzi na skok układu zamkniętego
4-Próby znalezienia lepszych nastaw metodą ręczną
Rozdział 28.2.2 Etap 1–Badanie odpowiedzi obiektu na skok w układzie otwartym
Rys. 28-1
Jest to typowy człon wieloinercyjny, tu czteroinercyjny
Na prawdziwym obiekcie nie znasz oczywiście tej transmitancji. Domyślasz się tylko, że jest to człon wieloinercyjny. Jakie jest to „wielo”, jakie są stałe czasowe? Tego nie wiesz. Dodam tylko, że dużo procesów, zwłaszcza w przemyśle chemicznym, ma taki charakter. Skup się na czarnym skoku x(t) i czerwonej odpowiedzi y(t). Widzisz charakterystyczne kolanko, inaczej punkt przegięcia. Przez ten punkt została poprowadzona styczna i z tej konstrukcji zostały wyznaczone parametry K, T i To transmitancji zastępczej Gp(s). Temat został dokładnie omówiony w rozdz. 10 Rys. 10-5.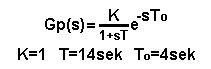
Rys.28-2
Wyznaczone parametry obiektu K T i To
Rozdział 28.2.3 Etap 2-Wyznaczenie z odpowiednich tabel nastaw optymalnych Kp, Ti i Td
Wg Pana Zieglera jest kilka optymalnych kombinacji Kp, Ti, Td dla tej samej odpowiedzi skokowej. Jak to? Przecież optymalny zestaw Kp, Ti i Td. Zwycięzca, może być tylko jeden. Święta prawda, ale jedno optimum jest dla najkrótszego czasu bez przeregulowań. Drugie to też najkrótszy czas, ale np. z przeregulowaniem 20%, a trzecie to kryterium minimum całki z kwadratu uchybu. Już sama nazwa trzeciego budzi niechęć. Dlatego nastroimy regulator wg kryterium nr 2 a ono rzecze tako:
Dla regulatora PID i obiektu z Rys. 28-3 następujące nastawy regulatora PID zapewnią najkrótszy czas regulacji przy przeregulowaniu nie większym niż 20%.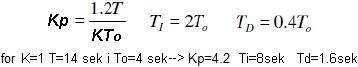
Rys. 28-3
Wzory i obliczone nastawy dla obiektu o parametrach z Rys. 28-2.
Są pewne ograniczenia. Mianowicie opóźnienie To musi być w zakresie 0.15T…0.6T. Czyli np. czysta inercja albo czyste opóźnienie odpada. Warunek jest oczywiście spełniony bo 2.1 sek<4 sek<8.4 sek. Sprawdźmy więc jak wygląda odpowiedź na skok z w/w nastawami.
Rozdział 28.2.4 Etap 3- Sprawdzenie odpowiedzi na skok układu zamkniętego
Rys. 28-4
Układ zamknięty z nastawami optymalnymi z Rys. 28-3.
Rys. 28-5
Co by tu powiedzieć? Po pierwsze przeregulowanie to 50% a nie 20%. Po drugie czas regulacji to ponad 1 min. Porządny regulator powinien dać odpowiedź szybszą niż układ otwarty (bez regulatora) na Rys.28-1.
To ja to sobie tak tłumaczę. Nastawy wyznaczone przez kryterium Zieglera-Nicholsa to tylko pierwsze przybliżenie. To tak jakby ktoś zabrał nas helikopterem w okolice Giewontu i powiedział. Teraz szukaj szczytu-optimum sam. Co prawda nie wysadził nas przy samym krzyżu na Giewoncie, ale znacznie ułatwił robotę. Zawęził się obszar poszukiwań. Dalej będziemy więc szukać nastaw optymalnych metodą prób i błędów z punktu startowego Kp=4.2 Ti=8 sek Td=1.6 sek. Będzie mniejsza liczba kombinacji Kp, Ti, Td do zbadania, niż gdybyśmy zaczynali z przypadkowego (czytaj „dalszego”) punktu startowego.
Rozdział 28.2.5 Etap 4-Próby znalezienia lepszych nastaw metodą ręczną
Wykonałem kilka prób z różnymi nastawami. W końcu znalazłem takie nastawy regulatora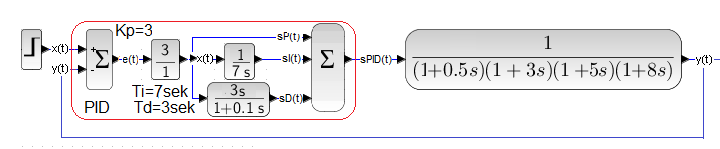
Rys. 28-6
Kp=3 Ti=7 sek Td=3 sek
Rys. 28-7
Jest poprawa? Jest. Nawet przeregulowanie jest w okolicach 20%. Ale dlaczego pierwszy strzał (Rys. 31-6) nie był trafiony? Próbowałem nieporadnie bronić Zieglera. Że to tylko pierwsze przybliżenie do optymalnych nastaw. Że parametry Kp, T, To nie zostały wyznaczone dokładnie, że… itd. Nie wiem.
Rozdział 28.3 – Metoda cyklu granicznego
Rozdział 28.3.1 Wstęp
W rozdziale 28.2 wyznaczyliśmy optymalne nastawy Kp, Ti i Td na podstawie modelu matematycznego opisującego obiekt. Nie ważne, że był to model uproszczony-transmitancja zastępcza Gp(s) typu inercja z opóźnieniem z Rys.28-1. Nie ważne, że powstał na podstawie doświadczenia, a nie rozważań teoretycznych. Ważne jest to, że korzystaliśmy z modelu obiektu. To była pierwsza szkoła strojenia regulatorów.
Metoda cyklu granicznego jest przykładem drugiej szkoły. Tu nie jest potrzebny model model. Wystarczy tylko zrobić „coś” obiektowi i obserwować jego zachowanie. Tym „cosiem” może być np. stopniowe zwiększanie wzmocnienia w układzie zamkniętym do momentu, w którym stanie się niestabilny. Innymi słowy – stanie się generatorem.
Rozdział 28.3.2 Próba nr 1

Rys. 28-8
Czym różni się schemat od Rys. 28-4?
1-Poprzez zera zostały wyłączone składowe – całkująca i różniczkująca. Czyli z regulatora PID zrobił się regulator P
2-Wymuszenie x(t) w 3 sekundzie jest teraz impulsem Diraca (właściwie pseudoimpulsem)
Przypominam, że układy niestabilne mogą się „nie ruszać”. Tak jak zaostrzony ołówek postawiony pionowo na stole. Może tak sobie stać do końca świata, chociaż jest to układ ewidentnie niestabilny. Dlatego żeby zaobserwować niestabilność, dajemy na wejście impuls Diraca.
Uwaga
Zaletą metody jest to, że dotyczy systemu zamkniętego. “Otwarcie” systemu zamkniętego, w celu jego badania, może być dla obiektu przemysłowego kłopotliwe.
Rys. 28-9
Pukneliśmy obiekt w nos młotkiem Diraca. Zabujało i układ wrócił ze stanu początkowego 0 do stanu końcowego (równowagi) 0.
Czyli dla K=3 system jest stabilny.
Rozdział 28.3.3 Próba nr 2
Schemat z Rys. 28-8, tylko Kp=5.
Rys. 28-10
Dłużej się buja. Wniosek-Zbliżyliśmy się do niestabilności ale układ nadal jest stabilny.
Rozdział 28.3.4 Próba nr 3
Schemat z Rys. 28-8, tylko Kp=6.27
Rys. 28-11
O!!! buja się bez końca ze stałą amplitudą. Wniosek-Jesteśmy na granicy stabilności. Co za przypadek, że wybraliśmy akurat Kp=6.27!
Okres oscylacji Tosc=16.3 sek.
Z tego doświadczenia zapamiętajmy 2 wartości:
– wzmocnienie Kp=6.27 które nazwiemy wzmocnieniem krytycznym Kkr=6.27
– okres oscylacji Tosc=16.3
Obydwa parametry będą potrzebne do wyznaczenia nastaw optymalnych Kp Ti i Td w rozdz. 28.3.7.
Dalsze zwiększanie wzmocnienia nie jest nam już potrzebne. Ale zróbmy to dla zwykłej ciekawości.
Rozdział 28.3.5 Próba nr 5
Schemat z Rys. 28-8,tylko Kp=6.5
Rys. 28-12
Tego się chyba spodziewaliśmy. Amplituda powoli rośnie do nieskończoności. Gdyby to był układ rzeczywisty, a nie liniowy idealny, to amplituda rosłaby do +/- nasycenia
Rozdział 28.3.6 Wyznaczenie parametrów optymalnych
Rys. 28-13
Parametry optymalne Kp, Ti i Td obliczamy wg. bardzo prostych wzorów–>Rys. 28-13a. Powinny zapewnić najkrótszy czas regulacji przy przeregulowaniu nie większym niż 30%. Gdy do tych wzorów podstawimy Kkr=6.27 i Tosc=16.3 sek z Rys.28-11 to otrzymamy nastawy optymalne –> Rys. 28-13b. Proponuję s prawdzić kalkulatorem.
Rozdział 28.3.7 Odpowiedź na skok przy nastawach optymalnych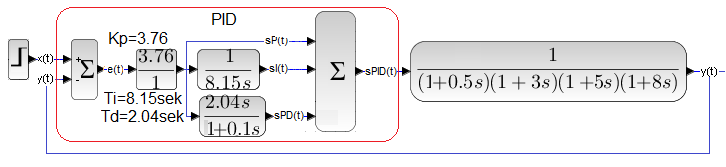
Rys. 28-14
Nastawy są z Rys. 28-13b, czyli są optymalne wg metody cyklu granicznego
Rys. 28-15
Nie rzuca na kolana, ale w porównaniu do poprzedniej Metody odpowiedzi skokowej z Rys.28-5 odpowiedź jest bliższa optymalnej. Oczywiście nie znaczy to, że metoda jest lepsza. Może przy innym obiekcie jest inaczej? Nie zajmę tu stanowiska.
Możemy próbować poprawić parametry metodą ręczną, tak żeby otrzymać odpowiedź nie gorszą niż powyżej.
