Podstawy automatyki
Rozdz. 27 Regulacja PID
Rozdz. 27.1 Wstęp
Wiemy już że:
– Regulacja P a tym bardziej PD szybko reaguje na skokową wartość zadaną x(t), ale uchyb ustalony e(t) jest zawsze niezerowy.
– Regulacja PI zapewnia zerowy uchyb regulacji, ale przebieg jest wolniejszy niż dla regulacji P, a tym bardziej PD.
Metoda narzuca się sama. Należy do regulatora PI dodać składową różniczkującą D. Okaże się, że przebieg będzie szybszy. W dodatku układ będzie bardziej stabilny. A co to oznacza? Że można np. zwiększyć wzmocnienie Kp regulatora dzięki czemu przebiegi będą jeszcze szybsze. Zaczniemy od badania struktury regulatora PID.
Rozdz. 27.2 Człon PID
To jeszcze nie regulator, bo nie realizuje jego najważniejszej funkcji, czyli porównania e(t)=x(t)-y(t).
Na razie wejściem jest tylko x(t) i badamy samą dynamikę.
Rozdz. 27.2.1 Człon PID gdy x(t) jest skokiem jednostkowym
Rys. 27-1
Człon PID
Kp=1 Ti=10 sek Td=1 sek
Realizowane 3 składowe sterujące:
-proporcjonalna sP(t)
-całkująca sI(t)
-różniczkująca sD(t)
Sygnałem wejściowym jest skok jednostkowy x(t).
Sygnał sPID(t) regulatora jest sumą składowych sP(t) sI(t) i sD(t).
Składowa proporcjonalna sP(t) to x(t) ponieważ Kp=1.
Składowa całkująca sI(t) narasta z taką prędkością, że po czasie Ti=10 sek zrówna się składową proporcjonalną sP(t). Tu akurat w 13 sekundzie, której nie widać bo doświadczenie kończy się w 10 sekundzie.
Składowa różniczkująca sD(t) – W 3 sekundzie występuje skok x(t) czyli w tym czasie prędkość jest nieskończenie wielka. I takie byłoby sD(t) dla idealnego człon różniczkującego D. A on jest rzeczywisty! Czyli „spłaszczony” przez człon inercyjny o stałej czasowej Td=0.1 sek. Ze względu na zakłócenia rzadko stosowany jest idealny człon różniczkujący D.
Składowe sP(t) i sI(t) są łatwe do interpretacji, gdy sygnał wejściowy x(t) jest skokiem. Gorzej jest z sD(t) ponieważ dla t=3 sek prędkość sygnału jest nieskończenie duża. Dlatego przeanalizujmy jeszcze raz PID, gdy x(t) narasta liniowo.
Rozdz. 27.2.2 Człon PID gdy x(t) narasta liniowo
Człon PID taki sam jak poprzednio, tylko x(t) jest sygnałem narastającym liniowo–>piła.
Rys. 27-2
Kp=1 Ti=10 sek Td=1 sek
Sygnał x(t) narasta liniowo.
Składowa proporcjonalna sP(t) też jest równa x(t)-czyli narasta liniowo
Składowa całkująca sI(t) jest funkcją parabolą bo całka z x(t) które narasta liniowo też jest jakimś kwadratem czasu t.
Widać ją, choć mniej wyraźnie, w sygnale wyjściowym regulatora sPID(t).
Rzeczywiste różniczkowanie sD(t) jest wyraźnie widoczne. Sygnał wejściowy x(t) narasta od 3 sekundy, ale jego stała prędkość została została „obliczona” z inercją dopiero po ok. 0.5 sekundzie. Czas ten jest widoczny na przebiegu składowej różniczkującej sD(t).
Sygnał sterujący Rozdz. sPID(t) jest oczywiście sumą:
sPID(t)=x(t)+sI(t)+sD(t)
ponieważ Kp=1
Poprzednio, czyli dla skoku x(t) łatwa była interpretacja Ti całkującego i trudniejsza Td różniczkującego.
Teraz przy „pile” x(t) jest odwrotnie.
Rozdz. 27.3 Regulator PID z obiektem jednoinercyjnym
Rozdz. 27.3.1 Obiekt jednoinecyjny
Regulatorem PID będziemy sterować obiekt ten sam obiekt jednoinercyjny co wcześniej, czyli o stałej czasowej T=10 sek. Rozpoczniemy od regulatora PID z wyłączoną akcją różniczkowania D, czyli tak na prawdę z regulatorem PI.
Rozdz. 27.3.2 Regulacja PID Kp=3 Ti=4 sek Td=0 – bez różniczkowania
Rys. 27-3
Kp=3 Ti=4 sek Td=0 sek
czyli jest to regulator PI
Przebieg jest taki sam jak w rozdz. 26 Rys. 26-13 ponieważ dotyczy tych samych układów regulacji! Zróbmy więc prawdziwą regulację PID dając na początek ostrożne różniczkowanie Td=0.5 sek.
Rozdz. 27.3.3 Regulacja PID Kp=3 Ti=4 sek Td=0.5 sek – to już prawdziwe PID!
Rys. 27-4
Kp=3 Ti=4 sek Td=0.5 sek
Gdzie tu pozytywny wpływ składowej różniczkującej? Nawet dłuższy czas regulacji. To zwiększmy na Td=1sek.
Rozdz. 27.3.4 Regulacja PID Kp=3 Ti=4 sek Td=1 sek
Rys. 27-5
Kp=3 Ti=4 sek Td=1 sek
Czas regulacji zwiększył się jeszcze bardziej. Widać, że dla Kp=3 i członu jednoinercyjnego składowa D nie poprawia przebiegów!
Dlaczego? Na początku skoku x(t) pojawia się „szpila” sygnału sterującego sPID(t) pochodząca głównie od składowej D. Potem „szpila” zanika ponieważ jest to człon różniczkujący rzeczywisty – czyli z inercją. Tu całej „szpili” nie widać, bo taki jest zakres oscyloskopu, ale spójrz np. na Rys. 27-1. „Szpila” prawie natychmiast „podbija” y(t). Czyli działa dobrze w kierunku przyspieszania przebiegu. Ale zaraz potem pojawia składowa „hamująca” D pochodząca od narastającego y(t). Powinna ona zapobiegać przeregulowaniom czyli przejściom y(t) na wartości większe od 1. Akurat dla członów jednoinercyjnych nie ma dużych przeregulowań y(t), co widać na załączonym obrazku. Pozostaje natomiast mechanizm hamowania, który wydłuża przebieg. Nieznacznie, ale wydłuża. Dlatego regulacja PID dla obiektów jednoinercyjnych nie poprawia specjalnie przebiegów. Wystarczy samo PI.
Jeszcze lepszą dynamikę da regulacja typu P ale niestety nie zapewni uchybu zerowego. Więcej o sile „przyspieszająco-hamującej” składowej różniczkującej D było w Rozdz. 24 Rys. 24-13.
Rozdz. 27.3.5 Regulacja PID Kp=10 Ti=5 sek Td=0 sek
Jak zwykłe zaczynamy od wyłączonej składowej D. Czyli badamy regulator PI. Dlaczego Ti=5 sek a nie Ti=4 sek jak poprzednio? Bo wcześniej stwierdziliśmy, że dla członu jednoinercyjnego i wzmocnienia Kp=10 optymalna nastawą Ti dla regulacji PI jest właśnie Ti=5 sek.
Rys. 27-6
Na razie najlepszy przebieg z dotychczasowych. Ale to nie zasługa D tylko wzmocnienia Kp! Czuję pismo nosem,że Td=0 będzie optymalne.
Rozdz. 27.3.6 Regulacja PID Kp=10 Ti=5 sek Td=0.5 sek
Rys. 27-7
Kp=10 Ti=5 sek Td=0.5 sek
Różniczkowanie nie poprawiło odpowiedzi. Dłuższy czas regulacji. Zwiększmy różniczkowanie na Td=1 sek.
Rozdz. 27.3.7 Regulacja PID Kp=10 Ti=5 sek Td=1 sek
Rys. 27-8
Kp=10 Ti=5 sek Td=1 sek
Jeszcze gorzej. Czyli dla Kp=10 najlepsza nastawa Td to Td=0 sek. Podobnie jak dla Kp=3.
Rozdz. 27.4 Regulator PID z obiektem dwuinercyjnym
Rozdz. 27.4.1 Obiekt dwuinecyjny
Obiekt Dwuinercyjny o stałych czasowych T1=3 sek i T2=5 sek poznaliśmy już wcześniej. Np. Rozdz. 26 Rys.26-20. Sterowanie rozpoczniemy od regulatora PID z wyłączona akcją różniczkowania D.
Rozdz. 27.4.2 Regulacja PID Kp=3 Ti=8 sek Td=0 – bez różniczkowania
Czyli regulacja PI
Rys. 27-9
Kp=3 Ti=8 sek Td=0 sek – bez różniczkowania
Zróbmy więc prawdziwą regulację PID dając na początku „ostrożne” różniczkowanie-Td=0.5 sek.
Rozdz. 27.4.3 Regulacja PID Kp=3 Ti=8 sek Td=0.5
Rys. 27-10
Kp=3 Ti=8 sek Td=0.5 sek
Nareszcie PID się popisał! Porównaj odpowiedź z poprzednią bez różniczkowania. Niebo a ziemia. Tak jak Małysz nie pokaże swojego kunsztu na skoczni 10-metrowej, tak PID nie zaimponuje sterując prostym obiektem inercyjnym. A tu proszę trudniejszy do sterowania obiekt dwuinercyjny i od razu widać efekt różniczkowania.
Przypomnę jak działa składowa różniczkująca D. Na początku skoku przyspiesza przebieg, bo różniczkowany jest skok x(t). Potem hamuje bo składowa różniczkująca dodatkowo ( oprócz P i I) zmniejsza sygnał sterujący i zapobiega w ten sposób przeregulowaniu. Zobacz jak skutecznie. Prawie nie ma oscylacji! A może jeszcze poprawimy przebieg zwiększając Td? Ale najpierw pokażę ten sam przebieg przy innych nastawach oscyloskopu po to żebyś zobaczył cały sygnał sterujący.
Rys. 27-11
Spodziewałem, że będzie „szpila”. Ale aż taka? Miej to z tyłu głowy, gdy analizujesz przebiegi regulacji PID lub PD. Co to oznacza? Piec potrzebuje np. 55 kW by osiągnąć temperaturę odpowiadającą y=1. Ale na początku przez chwilę daje moc ponad 18 razy większą czyli w okolicy 1 MW. Taka mała elektrownia. Chyba nie damy takiej mocy do projektowanego pieca. Na razie jesteśmy teoretykami. Modelujemy przebiegi nie przejmując się ograniczeniami. Wrócimy do tematu później w Rozdz.31.
Rozdz. 27.4.4 Regulacja PID Kp=3 Ti=8 sek Td=1sek
Rys. 27-12
Kp=3 Ti=8 sek Td=1 sek
Cudo, prawie bez oscylacji! Zwiększmy jeszcze Td. Może zobaczymy jeszcze większe cudo.
Rozdz. 27.4.5 Regulacja PID Kp=3 Ti=8 sek Td=5 sek
Zdrowo zwiększyliśmy różniczkowanie z Td=1 sek na Td=5 sek. Ciekawe jaki będzie efekt?
Rys. 27-13
Kp=3 Ti=8 sek Td=5 sek
Każda przesada je zła. Co prawda, tak jak oczekiwaliśmy „szpila” na początku skoku x(t) zwiększyła nam prędkość narastania y(t), ale potem zwiększyło się hamowanie od silnego różniczkowania D od y(t). Zbyt silne różniczkowanie y(t) („hamowanie”) przeważyło nad różniczkowaniem x(t) („przyspieszającym”). Co prawda przebieg stał się aperiodyczny (bez oscylacji) ale wydłużył się czas regulacji.
Rozpoczniemy teraz serię badań regulacji PID obiektu dwuinercyjnego ze wzmocnieniem Kp=10. Zaczniemy od Td=0 czyli od regulacji PI.
Rozdz. 27.4.6 Regulacja PID Kp=10 Ti=10 sek Td=0 sek
Rys. 27-14
Kp=10 Ti=10 sek Td=0 sek – bez różniczkowania
Ale buja! Żaden Klient nie wystawi faktury VAT za taki układ regulacji. Czy pomoże różniczkowanie D?
Rozdz. 27.4.7 Regulacja PID Kp=10 Ti=10 sek Td=0.5 sek
Zaczniemy ostrożnie od delikatnego różniczkowania czyli od Td=0.5 sek
Rys. 27-15
Kp=10 Ti=10 sek Td=0.5 sek
To było tylko bardzo ostrożne (czytaj-małe) różniczkowanie. Ale jak pięknie uspokoiło przebieg. Idźmy tą drogą i zwiększmy różniczkowanie.
Rozdz. 27.4.8 Regulacja PID Kp=10 Ti=10 sek Td=1 sek
Rys. 27-16
Kp=10 Ti=10 sek Td=1 sek
Jeszcze lepiej! Zwiększmy więc różniczkowanie na Td=2 sek
Rozdz. 27.4.9 Regulacja PID Kp=10 Ti=10 sek Td=2 sek
Rys. 27-17
Kp=10 Ti=10 sek Td=2 sek
Pozbyliśmy się co prawda przeregulowania, ale uchyb zerowy wystąpił dopiero po 25 sek. Tak jakbyśmy przesadzili z różniczkowaniem, które hamuje przebieg. Chyba poprzedni przebieg (Td=1 sek) był najlepszy? Czyżby? Zauważ że y(t) bardzo szybko doszedł do stanu w którym e(t)=0.05. Potem bardzo wolno maleje do 0. W tym czasie działa głównie całkowanie I. A może by tak przyspieszyć to całkowanie. Dajmy więc Ti=7 sek. Przy okazji zmniejszmy różniczkowanie na Td=1.5 sek.
Rozdz. 27.4.10 Regulacja PID Kp=10 Ti=7 sek Td=1.5 sek
Rys. 27-18
Kp=10 Ti=7 sek Td=1.5 sek
Autor!!! autor!!! Przyjmiemy więc nastawy Kp=10 Ti=7 sek Td=1.5 sek regulatora PID za optymalne dla naszego członu dwuinercyjnego. Porównaj jeszcze raz ten przebieg z Rys.27-14 który był realizowany przez regulator PI. Wynik jak w meczu Niemcy-Gibraltar.
Rozdz. 27.5 Regulator PID z obiektem trójinercyjnym
27.5.1 Wstęp
Obiekt trójnercyjny o stałych czasowych T1=0.5 sek T2=3 sek i T3=5 sek poznaliśmy już wcześniej. Np. Rozdz.26 Rys. 26-29.
Sterowanie obiektu rozpoczniemy od regulatora PID z wyłączona akcją różniczkowania D.
Rozdz. 27.5.2 Regulacja PID Kp=3 Ti=10 sek Td=0 sek – bez różniczkowania
Rys.27-19
Kp=3 Ti=10 sek Td=0 sek – bez różniczkowania
Zróbmy teraz prawdziwą regulację PID, dając na początku „ostrożne” różniczkowanie-Td=0.5 sek.
Rozdz.27.5.3 Regulacja PID Kp=3 Ti=10 sek Td=0.5 sek
Rys. 27-20
Kp=3 Ti=10 sek Td=0.5 sek Wciśnij „start”
Nawet takie słabe różniczkowanie korzystnie wpływa na przebieg. Sprawdźmy, czy opłaca się dalsze zwiększenie Td.
Rozdz. 27.5.4 Regulacja PID Kp=3 Ti=10 sek Td=1 sek
Rys. 27-21
Kp=3 Ti=10 sek Td=1 sek
Mniejsze przeregulowanie i czas regulacji poprawił się tylko trochę. Zwiększmy Td.
Rozdz. 27.5.5 Regulacja PID Kp=3 Ti=10 sek Td=1.5 sek
Rys. 27-22
Kp=3 Ti=10 sek Td=1.5 sek
Widać „hamujący” efekt różniczkowania. A poprawa dyskusyjna. Na plus działa brak przeregulowań. Na minus, że pole pod zielonym e(t) (czyli całka z uchybu) jest chyba trochę większe.
Przejdźmy teraz do Kp=10. Na początek bez różniczkowania.
Rozdz. 27.5.6 Regulacja PID Kp=10 Ti=10 sek Td=0 sek bez różniczkowania
Rys. 27-23
Kp=10 Ti=10 sek Td=0 sek bez różniczkowania
Spodziewaliśmy się takich oscylacji po zwiększeniu Kp. W celu „uspokojenia” damy różniczkowanie D.
Rozdz. 27.5.7 Regulacja PID Kp=10 Ti=10 sek Td=1 sek
Rys. 27-24
Kp=10 Ti=10 sek Td=1 sek
Pięknie. Składowa D spełniła nasze oczekiwania. To podkręćmy ją jeszcze Td.
Rozdz. 27.5.8 Regulacja PID Kp=10 Ti=10 sek Td=2 sek
Rys. 27-25
Kp=10 Ti=10 sek Td=2 sek
Lepiej. Irytuje jeszcze długie dochodzenie do stanu ustalonego e(t)=0. A może by tak zwiększyć prędkość całkowania np. na Ti=7 sek?
Rozdz. 27.5.9 Regulacja PID Kp=10 Ti=7 sek Td=2 sek
Rys. 27-26
Kp=10 Ti=7 sek Td=2 sek
Poprawa. A jeśli porównamy jeszcze z regulacją typu PI (albo PID gdzie Td=0 sek) na Rys.27-23, to szok! Już nie mówiąc o regulacji P. Dlatego założymy, że optymalne nastawy regulatora PID dla sterowanego obiektu trójinercyjnego to Kp=10 Ti= 7sek Td=2 sek. Na pewno znajdą się lepsze przy badaniu większej ilości kombinacji Kp Ti Td. Wyznaczaniem optymalnych nastaw regulatora PID poświęcono mnóstwo opracowań. W rozdz. 28 omówimy tylko te najprostsze.
Rozdz. 27.6 Regulacja PID z zakłóceniami
Rozdz. 27.6.1 Wstęp
Będą sterowane te same obiekty dwu- i trójinercyjne. Nie badamy jednoinercyjnych, bo w tym przypadku PID nie jest lepsze od PI. Zastosowane będą te nastawy które dawały „najładniejszą” odpowiedź. „Najładniejszą” tzn. względnie szybką i z możliwie małymi oscylacjami. Nazwiemy je z pewną przesadą optymalnymi.
Rozdz. 27.6.2 Dwuinercyjny zakłócenie dodatnie z(t)=+0.5, Kp=10, Ti = 7 sek Td=1.5 sek
Rys.27-27
Regulator optymalny ze względu na x(t), czyli z Rys.27-18. Zakłócenie z(t)=+0.5 pojawi się w 70 sekundzie. Do 70 sekundy, czyli do pojawienia się zakłócenia, przebieg jest taki sam jak na Rys.27-18, biorąc oczywiście pod uwagę inną skalę czasu na oscyloskopach. Początkowo zakłócenie z(t)=+0.5 spowodowało wzrost sygnału y(t) ale potem sygnał sterujący sPID(t) „zmusił” y(t) do powrotu do poprzedniej wartości, czyli do y(t)=1. Odpowiada to odpowiedniemu sprowadzeniu uchybu e(t) do 0. Pięknie widać, jak na dodatkowe grzanie z(t)=+0.5 regulator PID w stanie ustalonym zareagował chłodzeniem sPID(t)=-0.5. Składowa D poprawia dynamikę przebiegu.
Uwaga!
W odpowiedzi na zakłócenie z(t)=+0.5, sygnał sterujący sPID(t) pokrywa się w stanie ustalonym z zakłóceniem z(t)=+0.5. Dotyczy to także następnych przykładów, w których z(t)=+0.5.
Rozdz. 27.6.3 Dwuinercyjny zakłócenie ujemne z(t)=-0.5, Kp=10, Ti = 7 sek Td=1.5 sek
Rys. 27-28
Zakłócenie z(t)=-0.5 pojawi się w 70 sekundzie.
Do 70 sekundy, czyli do pojawienia się zakłócenia, przebieg jest taki sam jak na Rys. 27-27. Początkowo zakłócenie z(t)=-0.5 spowodowało spadek sygnału y(t) ale potem sygnał sterujący sPID(t) „zmusił” y(t) do powrotu do poprzedniej wartości, czyli do y(t)=1. Odpowiada to odpowiedniemu sprowadzeniu uchybu e(t) do 0. Na ujemne zakłócenie -„chłodzenie”, sterowanie sPID(t) zareagowało zwiększeniem mocy-„grzaniem”.
Rozdz. 27.6.4 Trójinercyjny zakłócenie dodatnie z(t)=+0.5,Kp=10, Ti = 7 sek Td=2 sek
Rys. 27-29
Zakłócenie z(t)=+0.5 pojawi się w 70 sekundzie.
Obiekt jest trudniejszy do sterowania i chociaż PID robi większe wygibasy niż dla dwuinercyjnego to efekt jest nieco gorszy. Analizę następnego doświadczenia z zakłóceniem ujemnym z(t)=-0.5 pozostawiam Czytelnikowi.
Rozdz. 27.6.5 Trójinercyjny zakłócenie ujemne z(t)=-0.5,Kp=10, Ti = 7 sek Td=2 sek
Rys. 27-30
Zakłócenie z(t)=-0.5 pojawi się w 70 sekundzie.
Odpowiedź y(t) na wartość zadaną x(t) i zakłócenie ujemne z(t)=-0.5
Rozdz. 27.7 Porównanie regulatorów P, PD, PI i PID
27.7.1 Wstęp
Porównamy regulacje P, PD, PI i PID podając jednocześnie skok x(t) na 4 układy regulacji sterujące tym samym obiektem:
– dwuinercyjnym
– trójinercyjnym
Optymalne nastawy regulatorów zostały przez nas dobrane wcześniej.
Rozdz. 27.7.2 Układy regulacji z obiektem dwuinercyjnym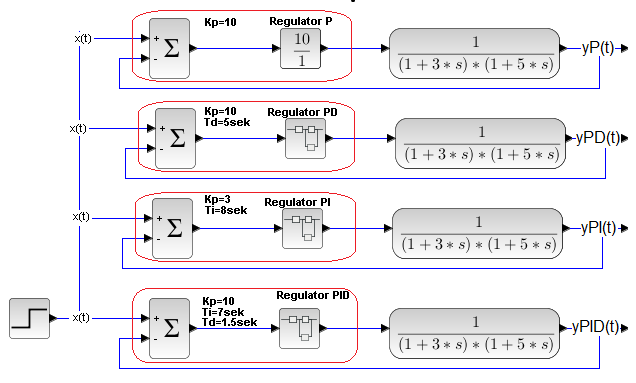
Rys. 27-31
Wcześniej badałeś te obiekty z optymalnymi nastawami w rozdziałach:
– 26 regulacja P
– 27 regulacja PD
– 29 regulacja PI
– 30 regulacja PID
Tu mamy ich uboższe wersje ze wspólnym sygnałem wejściowym x(t) i pojedynczym wyjściem yP(t), yPD(t), yPI(t) i yPID(t) z każdego sterowanego obiektu.
Rys. 27-32
Czarne yP(t) regulacji P jest najgorsze. Ma najwięcej oscylacji, trwa długo i nie zapewnia zerowego uchybu
Zielone yPD(t) regulacji PD ma najlepszą dynamikę – odpowiedź prawie prostokątna. Też nie zapewnia zerowego uchybu.
Niebieskie yPI(t) regulacji PI zapewnia już zerowy uchyb, ale długi czas regulacji i oscylacje
Czerwone yPID(t) ma najwięcej zalet. Zerowy uchyb, krótki czas regulacji i małe oscylacje.
Porównaj teraz efekty pracy wypasionego regulatora PID i jego ubogiego krewnego P.
Rozdz. 27.7.3 Układy regulacji z obiektem trójinercyjnym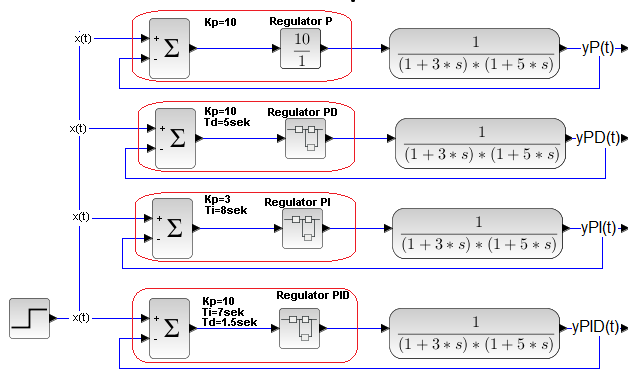
Rys. 27-33
Rys. 27-34
Przebiegi czasowe są gorsze niż poprzednio, bo sam obiekt jest trudniejszy do sterowania. Wnioski ogólne pozostają takie same.
Rozdz. 27.8 Podsumowanie regulacji PID
PID jest królem wszystkich regulatorów. Nawet dla niektórych pojęcia PID i regulator znaczą to samo. Podobnie jak elektroluks i odkurzacz.
Koncepcja PID-u nie wzięła się z wysublimowanych rozważań matematycznych lecz z prostych obserwacji. Np jak sternik stara się utrzymać kurs statku pomimo zakłóceń takich jak fale, wiatr. Także zmiana kursu to też nic innego jak odpowiedź układu regulacji na skok jednostkowy.
W życiu codziennym człowiek posługuje się algorytmem typu PID w którym składowa:
–P to natychmiastowa reakcja na zdarzenie typowa dla ludzi młodych
–I to reakcja która bierze pod uwagę doświadczenie życiowe z podobnymi przypadkami w przeszłości. Nie bądź nerwus, reaguj stopniowo. Jak cię coś uwiera (uchyb e(t)) to delikatnie działaj w odpowiednim kierunku i czekaj na efekty. Typowa dla osób starszych
–D to zdolność przewidywania przyszłości. Reakcja jest proporcjonalna do tendencji danego zjawiska. Wartość zadana narasta, to moja reakcja wynika nie tylko z samej wartości zadanej x(t) ale także z jej prędkości. Z drugiej strony, gdy x(t) już się ustali, to chcąc zapobiec przeregulowaniom, zaczynam hamować nawet gdy y(t) nie osiągnęło jeszcze wartości zadanej x(t). Bo y(t) zbyt szybko rośnie!
Reakcje typu PID dotyczą nie tylko techniki.
W ekonomii makler podejmuje decyzję do zakupu/sprzedaży akcji danej firmy, której po cenie która będzie wynikała z:
– aktualnej ceny akcji–>(P)
– wiedzy o otychczasowym zachowaniu się akcji, szerzej firmy–>(I)
– tendencji wzrostu/ spadku ceny–>(D)
Dla pełnej analogii kupno akcji to sygnał dodatni a sprzedaż to ujemny.
Są maklerzy którym powierzyłbyś swoją kasę (dobrze nastrojone regulatory PID) i kiepscy
.
