Podstawy automatyki

Rozdz. 25 Regulacja I

Rozdz. 25.1 Wstęp
Poznałeś już najprostszy regulator typu P składający się tylko z elementu porównującego i wzmacniacza Kp. Zapewniał z grubsza dochodzenie do wartości zadanej x(t) oraz tłumienie zakłóceń z(t). Potem pojawił się regulator PD który robił to samo, tylko dużo szybciej i z mniejszymi oscylacjami. W dalszym ciągu jednak wzmocnienie układu zamkniętego w stanie ustalonym Kz i wzmocnienie uchybowe Ku było takie:

Rys. 25-1
Ze wzorów wynika, że Kz jest zawsze trochę mniejsze od 1 . Tym bliższe 1 im większe K. Analogicznie Ke jest zawsze trochę większe od 0. Tym bliższe 0 im większe K. Przypominam, że K to jest wzmocnienie ustalone całego otwartego toru regulacji. Czyli uwzględniające Kp regulatora i Ko obiektu.
Tak się składa że jest przeważnie Ko=1, wtedy K=Kp. Jest to wygodne przy dobieraniu nastaw regulatora–> rozdz. 31.
A teraz najważniejsze!
Dla regulacji typu I wzory na Kz i Ke są następujące:

Rys. 25-2
Taniej, pardon prościej już się nie da! A co to oznacza? Jeżeli na wejście damy x(t) w postaci skoku jednostkowego, to po pewnym czasie będzie y(t)=x(t). Czyli uchyb e(t)=0! Taki jest główny cel każdego automatyka. Czas regulacji może być duży, mogą pojawić się też gasnące oscylacje . Ale gdy spełnione są pewne warunki dodatkowe (Hurwitz!.. Hurwittz!..) to zawsze tak się stanie. A gdy nie są spełnione? Wtedy układ jest niestabilny i oczywiście wzory z Rys. 25-2 nie obowiązują.
Uwaga
Wzory z Rys. 25-2 są właściwie szczególnym przypadkiem Rys. 25-1. Bo jakie jest wzmocnienie K obiektu z członem całkującym w stanie ustalonym. Czyli po czasie nieskończenie długim? K=nieskończoność! Podstaw tę wartość do Rys. 25-1 a otrzymasz Rys. 25-2.

Regulator I składa się z elementu porównującego i członu całkującego o regulowanym czasie całkowania Ti. Rzadko stosowane jest jako samodzielne urządzenie. Człon całkujący I występuje za to w regulatorach PI lub PID i jego celem jest sprowadzenie uchybu e(t) do zera.
Poznałeś go już wcześniej w rozdziale 4, tym nie mniej proponuję szybką powtórkę!

Rozdz. 25.2 Człon całkujący
Rozdz. 25.2.1 Wstęp
Zbadamy 3 człony o różnej prędkości całkowania
–„Wolny”
–„Taki sobie”
–„Szybki”
Nie są to jeszcze regulatory I, bo nie mają elementu porównującego obliczającego uchyb e(t)=x(t)-y(t)
Rozdz. 25.2.2 Człon I „Wolny” Ti=2 sek

Rys. 25-3
Ti=2sek
Człon całkujący o czasie całkowania Ti=2 sek. Sygnał narasta ze stałą prędkością. Ti=2 sek to czas po którym y(t) zrówna się z wartością skoku x(t). Następne człony będą „szybsze”. Dlatego ten ma nazwę „wolny”.
Rozdz. 25.2.3 Człon I „Taki sobie” Ti=1 sek

Rys. 25-4
Ti=1 sek
Po czasie Ti=1 sek y(t) zrównało się z wartością skoku x(t). Czyli 2 razy szybciej niż poprzednio.
Rozdz. 25.2.4 Człon I „Szybki” Ti=0.5 sek

Rys. 25-5
Ti=0.5 sek.
Po czasie Ti=0.5 sek y(t) zrównało się z wartością skoku x(t). Znowu 2 razy szybciej niż poprzednio.

Rozdz. 25.3 Serwomechanizm sprowadzający uchyb e(t) do 0, jako przykład regulacji typu I
Rozdz. 25.3.1 Wstęp
Jest to dobry przykład na to, że regulacja typu I sprowadza uchyb do 0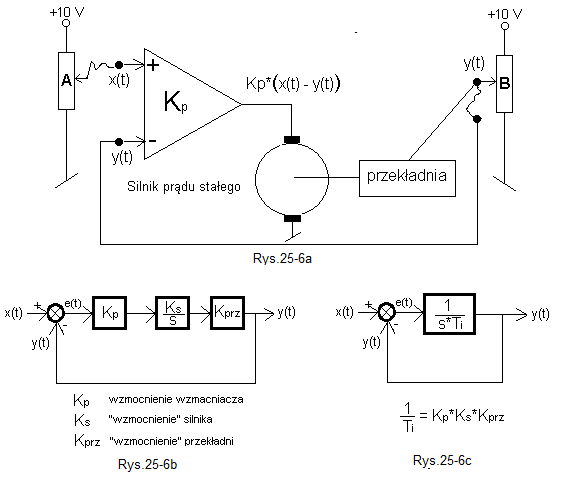

Rys. 25-6
Wielkością wejściową x(t) jest napięcie x(t) na potencjometrze A Rys. 25-6a. Silnik prądu stałego sterowany jest przez różnicę napięć e(t)=x(t)-y(t). Wał silnika jest sprzężony mechanicznie przez przekładnię z suwakiem potencjometru B. Silnik jest idealny, tzn. że gdy jest na nim napięcie nawet tak małe jak +1 µV, to suwak będzie się powolutku przesuwał do góry, czyli napięcie y(t) będzie powoli rosło. A gdy +2 µV to +2 razy szybciej. Analogicznie -1 µV to suwak będzie opadał. Jest to klasyczny człon całkujący , czyli człon I.
Suwak B stanie w miejscu tylko w jednej sytuacji. Gdy x(t)=y(t), czyli gdy napięcie na silniku będzie zerowe.
Na początku obydwa suwaki są na dole. Czyli x(t)=y(t)=0V i napięcie na silniku też jest zerowe, bo Kp*[x(t)-y(t)]= Kp*(0-0)V=0V i silnik stoi. Nagle ustawisz na potencjometrze A +5V. Tak jakbyś podał skok jednostkowy x(t)=+5V Wtedy silnik ruszy do góry z dużą prędkością początkową. Za chwilę prędkość się zmniejszy, bo na wejściu – wzmacniacza pojawi się napięcie „odejmujące” od suwaka. B
W ten sposób suwak B dojdzie do +5V po czasie teoretycznie nieskończenie długim. Napięcie na silniku będzie zerowe.
A co by było gdyby silnik z przekładnia miał bezwładność i suwak przekroczył by +5V. Np byłoby +5.1V. Wtedy pojawi się napięcie ujemne i suwak B cofnie się w kierunku +5V, aż po pewnym czasie znowu stanie na +5V.
Tak jest w świecie idealnym. W realu występują jakieś histerezy, strefy nieczułości i inne barachła, tak że suwak ustawiłby się np. na +4.999V. Wtedy bardzo małe napięcie na silniku nie byłoby w stanie go ruszyć.
Widzisz więc, że przy idealnych założeniach uchyb będzie zerowy, co jest typowe dla sterowania typu I.
Rys. 25-6b jest wersją blokową schematu z Rys. 25-6a. Tu Kp wzmacniacza jest oczywiste. Ks silnika jest tym większe im większą prędkość ma silnik przy danym napięciu. Parametr Kprz przekładni to jak przerzutka w rowerze.
W sumie jest to człon całkujący o jakimś czasie całkowania Ti objęty pętlą ujemnego sprzężenia zwrotnego–>Rys. 25-6c.
Rozdz. 28.3.2 Model serwomechanizmu wolnego
Serwomechanizm sprowadza się do bardzo prostego schematu z Rys. 25-6c.

Rys. 25-7
Serwomechanizm gdy Ti=4 sek (sprawdziłeś to np. doświadczalnie w układzie otwartym)
W 3 sekundzie ustawiłeś potencjometr A na 7.5 V. Czyli skok x(t)=7.5 V.
Serwomechanizm doszedł do stanu ustalonego y(t)=7.5 V po ok. 30 sekundach. Całkowanie I zapewniło uchyb ustalony e(t)=0!
Obiekt otwarty był członem całkującym o Ti=4 sek. Odpowiedź układu zamkniętego wygląda jak typowy człon inercyjny o Tz=4 sek. Tak też wynika załączonego wzoru na transmitancję układu zamkniętego. Trochę leniwy ten serwomechanizm.
Przyspieszmy go dając Ti=1 sek. Co to oznacza? Albo większe Kp, albo szybszy silnik czyli większe Ks, albo „szybsza” przekładnia Kprz-patrz na Rys. 25-6b.
Rozdz. 25.3.3 Model serwomechanizmu szybkiego

Rys. 25-8
Model serwomechanizmu gdy Ti=1 sek
Układ zareagował 4 razy szybciej. Do stanu ustalonego y(t)=7.5 V doszedł już po ok 7.5 sekundach.
Rozdz. 25.3.4 Wnioski z badania serwomechanizmu
W układzie regulacji pojawiło się całkowanie I, bo silnik prądu stałego jest członem całkującym. Spowodowało to doprowadzenie uchybu e(t) do zera. Jest to najważniejsza zaleta całkowania. W poprzednich rozdziałach składowa proporcjonalna P nie była w stanie sprowadzić uchybu do 0. Tu składowa I zrobiła to. Bo choćby nie wiem jak mały jest uchyb, to nawet bardzo małe napięcie zawsze będzie kręciło silnikiem tak by y(t)=x(t). Oczywiście teoretycznie. W praktyce strefa nieczułości i histereza silnika spowoduje jednak jakiś uchyb.

Rozdz. 25.4 Regulacja I z obiektem inercyjnym
Rozdz. 25.4.1 Wstęp
Zbadamy układ, w którym regulator I steruje obiektem inercyjnym o stałej czasowej T=10 sek. Zaczniemy od najostrożniejszej nastawy Ti=36 sek, potem Ti=16 sek i skończymy na Ti=8 sek. Będzie wymagana cierpliwość, bo czas doświadczenia to 2 minuty. Zaczniemy jak zwykle od badania samego obiektu inercyjnego.

Rys. 25-9
Obiekt inercyjny o stałej czasowej T=10 sek
Chyba wszystko jasne.
Rozdz. 25.4.2 Regulacja I gdy Ti=36 sek

Rys. 25-10
Jedyną nastawą regulatora jest Ti=36 sek. Zaczynamy od tak wolnego całkowania, bo obawiamy się oscylacji a nawet niestabilności. Chyba obawy były na wyrost. Układ bardzo wolno doszedł bez oscylacji ( inaczej – aperiodycznie) do stanu równowagi, gdzie x(t)=y(t). Czyli uchyb e(t)=0. Tak na prawdę to po 120 sek nie ma jeszcze stanu y(t)=1. Nastąpi to później. Ale chyba wierzysz, że tak będzie. Dopóki uchyb e(t) będzie różny od 0 (tu akurat większy od 0), dopóty regulator I będzie pchał sygnał do stanu w którym y(t)=x(t)=1. W teorii to nieskończenie długo, w praktyce po ok. 130 sek.
Rozdz. 25.4.3 Regulacja I gdy Ti=16 sek
Poprzedni przebieg był wołowaty. Szybsze całkowanie Ti=16 powinno poprawić sytuację.

Rys. 25-11
Regulacja typu I Ti=16 sek
Na początek radość wielka. Ponieważ s(t) szybciej rośnie to y(t) też robi to samo. Niestety pojawiła się oscylacja. Mimo wszystko po ok. 120 sek sygnał wyjściowy y(t) doszedł do stanu równowagi, w którym jak to regulację typu I przystało, uchyb ustalony jest zerowy. Czy odpowiedź jest znacznie lepsza od poprzedniej? Załóżmy, że tak pomimo oscylacji.
Rozdz. 25.4.4 Regulacja I gdy Ti=8 sek
Jeszcze bardziej skróćmy czas regulacji dając Ti=8. Może będzie lepiej?

Rys. 25-12
Regulacja typu I Ti=8 sek
Trochę krótszy czas regulacji lecz większe oscylacje. Przyjmiemy więc, że nastawa Ti=16 sek jest optymalną dla członu inercyjnego o stałej czasowej T=10 sek.

Rozdz. 25.5 Regulacja I z obiektem dwuinercyjnym
Rozdz. 25.5.1 Wstęp
Regulator I steruje obiektem dwuinercyjnym. Zaczniemy od badania samego obiektu. Już obiekt inercyjny okazał się trudny do sterowania, długi czas regulacji i oscylacje. Tu będzie będzie chyba jeszcze gorzej.

Rys. 25-13
Obiekt dwuinercyjny o stałych czasowych T1=3 sek i T2=5 sek
Widać punkt przegięcia charakterystyczny dla obiektów wieloinercyjnych. Z wykresu trudno odczytać parametry T1=3sek i T2=5sek.
Są na to sposoby, ale dajmy sobie spokój.
Rozdz. 25.5.2 Regulacja I gdy Ti=25 sek

Rys. 25-14
Regulacja typu I Ti=25 sek
Zaskoczenie. Przebieg wyraźnie lepszy od „łatwiejszej” regulacji I dla członu inercyjnego z Rys. 28-17!
Byłem przygotowany na gorszą odpowiedź y(t). A może ktoś to wyjaśni?
Rozdz. 24.5.3 Regulacja I gdy Ti=15 sek

Rys. 25-15
Jeżeli nie zależy nam na oscylacjach, to jest lepiej. Krótszy czas regulacji.
Rozdz. 28.5.4 Regulacja I gdy Ti=6 sek
A niech tam. Dajmy bardzo szybkie całkowanie Ti=6 sek.

Rys. 25-16
Regulacja typu I Ti=6 sek
Jednak przesadziliśmy. Nie dość, że długi czas regulacji, to dyndanie jest nie do przyjęcia.
Przyjmiemy więc, że nastawa Ti=15 sek jest optymalną dla członu dwuinercyjnego o stałych czasowych T1=3 sek i T2 = 5 sek.

Rozdz. 25.6 Regulacja I z obiektem trójinercyjnym
25.6.1 Wstęp
Najpierw sam obiekt.

Rys. 25-17
Obiekt trójinercyjny o stałych czasowych T1=0.5 sek, T2=3 sek i T3=5 sek.
Odpowiedź podobna dla dwuinercyjnego z Rys. 28-23, chociaż dobrze wiemy, że trójnercyjny jest trudniejszy do sterowania.
Rozdz. 25.6.2 Regulacja I gdy Ti=30 sek
Zaczniemy od ostrożnego sterowania, czyli wolnego całkowania Ti=30 sek.

Rys. 25-18
Regulacja typu I Ti=30 sek
Widać to ostrożne sterowanie. Sygnał sterujący s(t) jest niewiele większy od y(t).
Tak jak mało wymagający od ucznia nauczyciel. Dlatego odpowiedź jest wolna i bez oscylacji.
Rozdz. 25.6.3 Regulacja I gdy Ti=10 sek

Rys. 25-19
Regulacja typu I Ti=10 sek
Czas regulacji krótszy chociaż pojawiły się oscylacje.
Rozdz. 25.6.4 Regulacja I gdy Ti=5 sek

Rys. 25-20
Regulacja typu I Ti=5 sek
Straszne oscylacje. Przyjmiemy więc, że nastawa Ti=10 sek jest optymalną dla tego członu trójinercyjnego
Rozdz. 25.6.5 Gdy przesadzimy z całkowaniem
Czyli z prędkością całkowania np. Ti = 1.5 sek

Rys. 25-21
Regulacja typu I Ti=1.5 sek
Tego nie widać, ale jest inna skala oscyloskopu. Domyślasz się dlaczego?
Piękna niestabilność. Amplituda drgań rośnie do +/ nieskończoności.-

Rozdz. 25.7 Regulacja I z zakłóceniami.
25.7.1 Wstęp.
Sterowane będą te same 3 obiekty. Na ich wejścia będą działały duże zakłócenia z(t)=+0.5 lub z(t)=-0.5. Spowodowany przez nie uchyb e(t) tak będzie „denerwował” składową całkującą I, że ta zawsze sprowadzi go do 0. Trzeba się tylko uzbroić się w cierpliwość, ponieważ z powodu wolnych przebiegów typowych dla regulacji typu I, eksperymenty będą trwały do 4 minut.
Rozdz. 25.7.2 Inercyjny zakłócenie dodatnie z(t)=+0.5, Ti = 16 sek.

Rys. 25-22
Zakłócenie z(t)=+0.5 pojawi się w 130 sekundzie.
Do 130 sekundy, czyli do pojawienia się zakłócenia, przebieg jest taki sam jak na Rys. 28-19, biorąc oczywiście pod uwagę inną skalę czasu na oscyloskopach. Początkowo zakłócenie z(t)=+0.5 spowodowało wzrost sygnału y(t) ale potem składowa I „zmusiła” y(t) do powrotu do poprzedniej wartości, czyli do y(t)=1. Odpowiada to odpowiedniemu sprowadzeniu uchybu e(t) do 0. Na dodatnie zakłócenie -„grzanie”, sterowanie s(t) zareagowało zmniejszeniem mocy.
Rozdz. 25.7.3 Inercyjny zakłócenie ujemne z(t)=-0.5, Ti = 16 sek.

Rys. 25-23
Zakłócenie z(t)=-0.5 pojawi się w 130 sekundzie.
Na ujemne zakłócenie -„chłodzenie”, sterowanie s(t) zareagowało zwiększeniem mocy. Uchyb e(t) został sprowadzony do 0.
Rozdz. 25.7.4 Dwuinercyjny zakłócenie dodatnie z(t)=+0.5, Ti =15 sek.

Rys. 25-24
Zakłócenie z(t)=+0.5 pojawi się w 130 sekundzie.
Na dodatnie zakłócenie z(t)=+0.5 -„grzanie”, sterowanie s(t) zareagowało zmniejszeniem mocy.
Rozdz. 25.7.5 Dwuinercyjny zakłócenie ujemne z(t)=-0.5, Ti =15 sek.

Rys. 25-25
Zakłócenie z(t)=-0.5 pojawi się w 130 sekundzie.
Na ujemne zakłócenie -„chłodzenie”, sterowanie s(t) zareagowało zwiększeniem mocy.
Rozdz. 25.7.6 Trójinercyjny zakłócenie dodatnie z(t)=+0.5, Ti =10 sek.

Rys. 25-26
Zakłócenie z(t)=+0.5 pojawi się w 130 sekundzie.
Na dodatnie zakłócenie dodatnie z(t) -„grzanie”, sterowanie s(t) zareagowało zmniejszeniem mocy.
Rozdz. 25.7.7 Trójinercyjny zakłócenie ujemne z(t)=-0.5, Ti =10 sek.

Rys. 25-27
Zakłócenie z(t)=-0.5 pojawi się w 130 sekundzie.
Na ujemne zakłócenie z(t) -„chłodzenie”, sterowanie s(t) zareagowało zwiększeniem mocy.

Rozdz. 25.8 Porównanie regulacji typu I, P i PD.
Rozdz. 25.8.1 Wstęp.
Regulatory typu PD, P oraz I będą sterować obiektem dwuinercyjnym . Na ich wejścia będą podane w 3 sekundzie skoki jednostkowe x(t) a w 120 sekundzie zakłócenie dodatnie z(t)= +0.5 lub ujemne z(t)=-0.5.
Porównamy sygnały wyjściowe y1(t), y2(t) i y3(t), a zwłaszcza ich stany ustalone oraz czasy regulacji. Będziemy obserwować tylko skok jednostkowy x(t), zakłócenie z(t) i 3 sygnały wyjściowe y1(t), y2(t) i y3(t). Pominięte sygnały e(t) i s(t) były już obserwowane we wcześniejszych doświadczeniach.
Rozdz. 28.5.2 Zakłócenie dodatnie z(t)=+0.5.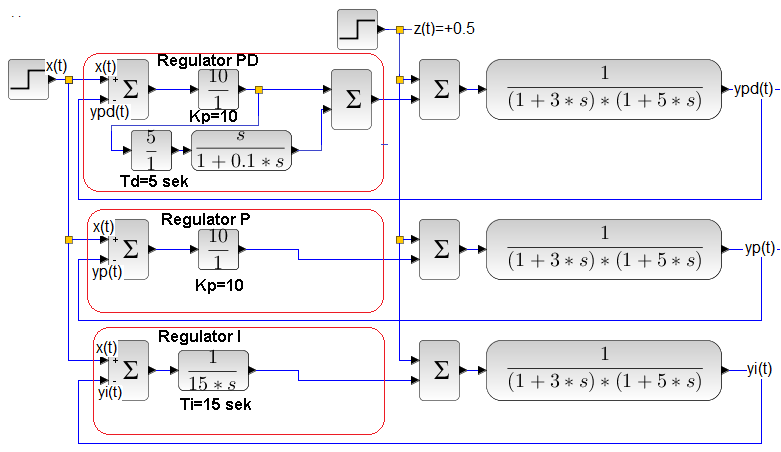

Rys. 25-28
Nastawy regulatora Kp=10 regulatorów PD i P zgodnie ze wzorem na Ke z Rys. 28-1 zapewnią uchyb ustalony e(t)=9%. Dodatkowo nastawa Td=5 sek regulatora PD da nam możliwie krótki czas regulacji z niewielkim przeregulowaniem.
Regulator I zapewnia zerowy uchyb ustalony e(t) niezależnie od nastawy Ti.

Rys. 25-29
Regulacja typu PD-zielona. jest najszybsza, chociaż daje niezerowy uchyb ustalony.
Regulacja typu P-niebieska. jest wolniejsza oraz z przeregulowaniami i też daje taki sam niezerowy uchyb ustalony.
Regulacja typu I-czerwona. jest najwolniejsza, za to zapewnia zerowy uchyb ustalony. I to jest właśnie podstawową zaletą regulacji typu I, czyli całkującej.

Rozdz. 28.8.3 Zakłócenie ujemne z(t)=-0.5.
Schemat taki sam jak na Rys.25-28 tylko zakłócenie ujemne tzn. z(t)=-0.5

Rys. 28-30
Analizę pozostawiam Czytelnikowi.

Rozdz. 28.8. Wnioski.
Dlaczego regulacja typu I jest tak wolna? Popatrz na sygnały sterujące s(t) we wcześniejszych eksperymentach. Dla P a tym bardziej dla PD są one duże na początku x(t) i z(t). To właśnie decyduje o szybkim czasie regulacji. W dodatku w przypadku PD składowa różniczkująca daje efekt hamowania zapobiegający oscylacjom. Tego początkowego kopa s(t) nie ma regulacja I.
Co by tu zrobić, żeby układ w miarę szybko doszedł do stanu ustalonego, ale z zerowym uchybem ustalonym? Metoda narzuca się sama.
Kombinacja regulatora P z regulatorem I dająca regulator PI–>rozdz. 26.
Albo jeszcze lepiej – kombinacja PD z regulatorem I dająca regulator PID–>rozdz.27.