Podstawy automatyki

Rozdz. 17 Niestabilność, czyli jak powstają drgania

Rozdz. 17.1 Wstęp
Drgania wynikają po prostu z rozwiązania równań różniczkowych opisujących człon dynamiczny ze sprzężeniem zwrotnym. Otrzymasz przebieg który, w odpowiedzi na skok jednostkowy x(t),  wyjście y(t) dochodzi do stanu ustalonego y:
– bez oscylacji
– z gasnącymi oscylacjami
Przy pewnych parametrach, w tym wzmocnieniu K, może też powstać stan niestabilny z rosnącymi oscylacjami. 

Rys. 17-1
Stan ustalony y w układzie zamkniętym gdy G(s) statyczne lub astatyczne. Przypominam, że układ statyczny G(s) nie ma członu całkująceg0 (brak s  mianowniku) a układ astatyczny G(s) ma! (jest s w mianowniku).
W stanie ustalonym y(t)=y jest stałe. Takie układy nazywamy stabilnymi. Ale nie zawsze tak jest. Przy pewnych parametrach transmitancji G(s), zwłaszcza przy dużym K i dużych opóźnieniach powstaną drgania y(t) o stałej lub rosnącej amplitudzie. Mamy wtedy do czynienia z układami niestabilnymi.
Można oczywiście poprzestać na tym, że przy pewnych parametrach G(s) układ jest stabilny, a przy innych niestabilny. Takie są rozwiązania równań różniczkowych i już. Takie podejście powoduje jednak pewien niedosyt. Dlatego spróbujmy przeanalizować problem „na chłopski rozum”. Podejrzewamy, że drgania wynikają z bezwładności układu, z tego że odpowiedź pojawia się z pewnym opóźnieniem.
Przykład
Płyniesz żaglówką z Wilkas poprzez jezioro Niegocin do Giżycka. Jest noc, wicher dmie i kierujesz się na latarnię morską (jeziorną?). Dla uproszczenia załóżmy, że używasz tylko steru-szot grota pomijamy. Sterowanie jest proste. Latarnia tyci tyci w prawo od twojego kursu to kontrujesz sterem (też tyci tyci) w lewo i vice versa. Jeżeli nie ma zakłóceń typu wiatr, fale itd, to płyniesz prawie po linii prostej na latarnię. Przy okazji. Między sterem a kątem kursu jest zależność typu całkującego, która może sprowadzić uchyb do zera. Doświadczony żeglarz płynie po linii prostej prawie niewidocznym wężykiem. A teraz wyobraź sobie, że między rumplem (czyli tym co trzymasz w ręku), a samą płetwą sterową jest człon opóźniający. Jak to urządzenie jest zbudowane – nieważne. Ważne jest to, że Twoje ruchy ręką są opóźnione np. o To=10 sek.. Małe uderzenie wiatru spowoduje zmianę kursu. Ty natychmiast kontrujesz. Efekt będzie widoczny dopiero po To=10 sek. Wtedy  zaczniesz płynąć już nie wężykiem ale wielkim wężem boa. Przy dużym To kurs może się nawet całkowicie rozjechać. Nie dopłyniesz, oj nie dopłyniesz do Giżycka. Z rejsu wyciągniemy ważny i dość oczywisty wniosek. Obiekty z dużymi bezwładnościami i opóźnieniami są trudniejsze do sterowania. Mogą spowodować wężyk, pardon oscylacje.
Skończmy jednak z żeglarstwem i rozważmy działanie czystego członu opóźniającego ze wzmocnieniem K i sprzężeniem zwrotnym. W takim układzie powstawanie drgań jest najłatwiejsze do zrozumienia.

Rozdz. 17.2 Niestabilność członu opóźniającego ze sprzężeniem zwrotnym
17.2.1 Wstęp
Możliwa jest analiza układu bez użycia rachunku różniczkowego. Prawie na palcach. Dojdziemy do ciekawego wniosku, przypominającego trochę Kryterium Nyquista, o którym zresztą będzie mowa w następnym rozdziale.
Układ otwarty z opóźnieniem po zamknięciu pętlą ujemnego sprzężenia zwrotnego będzie:
-stabilny gdy K<1
-niestabilny gdy K>1
-na granicy stabilności gdy K=1
Najpierw zbadamy sam człon opóźniający. Robiliśmy to już kiedyś, ale powtórka nie zaszkodzi. Podobno repetitio est mater studiorum.
Rozdz. 17.2.2 Badanie członu opóźniającego w układzie otwartym

Rys. 17-2
Człon opóźniający transmitancja której typ  wyraźnie różni się od typowych transmitancji G(s)

Rys. 17-3
Odpowiedź y(t) powyższego członu opóźniającego  G(s)=exp(-1s) jest dokładną kopią wejścia x(t) z opóźnieniem To=1 sek.
Rozdz. 17.2.3 Człon opóźniający w układzie zamkniętym K=0.75 i To=1sek
Zamknijmy człon opóźniający pętlą ujemnego sprzężenia zwrotnego.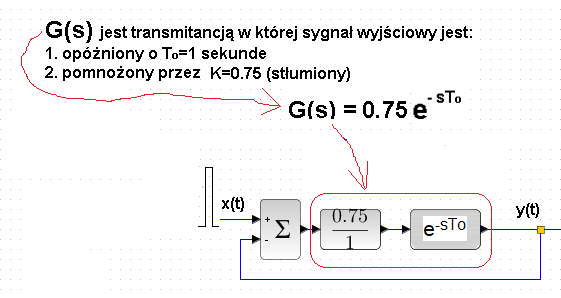

Rys. 17-4
Przed członem opóźniającym został umieszczony dodatkowo człon proporcjonalny, którego wzmocnienie K=0.75.

Rys. 17-5
W 5 sekundzie pojawia się impuls prostokątny x(t)=1.
W tym czasie y(t)=0, dlatego na wejściu G(s) za węzłem porównującym, też będzie ten sam impuls prostokątny 0.75*x(t)=+0.75.
W 6 sekundzie
y(1) = 0.75*x(0) = +0.75
Od 6 sekundy węzeł porównujący tylko odwraca fazę, bo x(n)=0 oraz e(n)=x(n)-y(n)=-y(n) .
Kolejny sygnał za członem opóźniającym będzie więc liczony wg. wzoru y(n+1)= – 0.75*y(n)
y(2) = – 0.75*y(1)= – 0.75*0.75= – 0.5625
y(3) = – 0.75*y(2)= + 0.422
y(4) = – 0.75*y(3)= – 0.316
y(5) = – 0.75*y(4)= + 0.237
y(6) = – 0.75*y(5)= – 0.180
y(7) = – 0.75*y(6)= + 0.133
y(8) = – 0.75*y(7)= – 0.100
y(9) = – 0.75*y(8)= + 0.075
itd…
Podkreślam że:
y(2) obliczyliśmy na podstawie znanego y(1),
y(3) obliczyliśmy na podstawie znanego y(2),
…itd
Jest to tzw. metoda rekurencyjna.
Kolejne impulsy y(n) są coraz mniejsze i dążą do zera. Wymuszenie typu impuls, wytrąciło więc układ z równowagi i powstały drgania zanikające o okresie To=1 sek.
Z matematycznego punktu widzenia ciąg y(1), y(2), y(3),…, y(n) jest postępem geometrycznym, w którym:
y(1) = 0.75
Iloraz tego postępu q=- 0.75
Ponieważ |q|<1, to ciąg dąży do 0.
W badanej transmitancji było K=0.75<1 . A gdyby tak K=1?
Rozdz. 17.2.4 Człon opóźniający w układzie zamkniętym K=1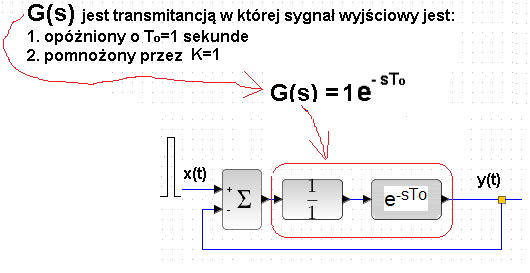

Rys. 17-6
W 5 sekundzie pojawia pojedynczy impuls x(t)

Rys. 17-7
Podobnie jak dla Rys. 17-5:
y(1) = x(t) = +1
y(2) = -1*y(1) = – 1
y(3) = -1*y(2) = +1
y(4) = -1*y(3) = – 1
y(5) = -1*y(4) = +1
y(6) = -1*y(5) = – 1
…itd
Impuls też wytrącił układ z równowagi, ale tym razem powstały drgania niegasnące o stałej amplitudzie. Układ stał się generatorem!
Tak więc dla układów z opóźnieniem i ze wzmocnieniem K=1, układ jest na granicy stabilności.
A gdyby tak K>1 np. K=1.25?
Rozdz. 17.2.5 Człon opóźniający w układzie zamkniętym K=1.25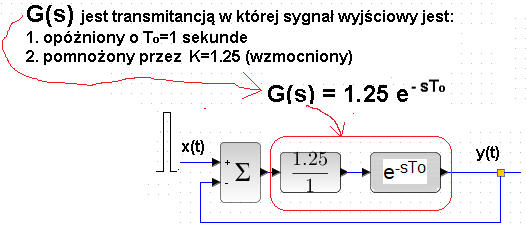

Rys. 17-8
W 5 sekundzie pojawia pojedynczy impuls x(t).

Rys. 17-9
Powstały drgania których amplituda dąży do +/- nieskończoności!
Musiały powstać bo:
y(1) = 1.25*x(t) = + 1.250
y(2) = -1.25*y(1) = – 1.562
y(3) = -1.25*y(2) = + 1.953
y(4) = -1.25*y(3) = – 2.441
y(5) = -1.25*y(4) = + 3.051
y(6) = -1.25*y(5) = – 3.815
y(7) = -1.25*y(6) = + 4.768
y(8) = -1.25*y(7) = – 5.960
y(9) = -1.25*y(8) = + 7.451
…itd
Rozdz. 17.2.6 Wnioski

Rys.17-10
Jeżeli człon opóźniający obejmiemy pętlą ujemnego sprzężenia zwrotnego i damy na wejście jakiś sygnał np. pojedynczy impuls to odpowiedzią będą drgania
o okresie To i amplitudzie:
-malejącej do 0..gdy k<1 – układ stabilny
-stałej…………..gdy k=1 – układ na granicy stabilności
-rosnącej………gdy k>1 – układ niestabilny
Zauważ, że na podstawie znajomości transmitancji układu otwartego określiliśmy stabilność układu zamkniętego.
Przypomina to trochę kryterium Nyquista –> Rozdz.18.

Rozdz. 17.3 Niestabilność członu trójinercyjnego ze sprzężeniem zwrotnym
Rozdz. 17.3.1 Wstęp
Poprzednio badaliśmy człon opóźniający z ujemnym sprzężeniem zwrotnym. Był on na tyle prosty, że korzystaliśmy tylko z matematyki elementarnej i intuicji. Zwiększając wzmocnienie K układ stał niestabilny. Źródłem tego było opóźnienie To. W układach ciągłych też tak jest, ale pojęcie opóźnienie należy zastąpić inercją. Gdy pojawia się wiele inercji T1, T2,T3…, tak jak np. w członie trójinercyjnym, to wystąpi coś w rodzaju opóźnienia To. Wtedy G(s) można przybliżać transmitancją zastępczą–>patrz Rozdz.10.2.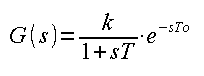

Rys. 17-11
Transmitancja zastępcza
Dla małego T transmitancja zastępcza staje się podobna do idealnego członu opóźniającego ze wzmocnieniem k na Rys. 17-3.
Umówmy się, że przy badaniu niestabilności, człon trójinercyjny jest reprezentantem wszystkich ciągłych G(s). Tu może powstać pytanie. To dlaczego nie jest nim jeszcze prostszy człon dwuinercyjny, oscylacyjny już nie mówiąc o inercyjnym. Analiza będzie łatwiejsza.
Otóż jak się później okaże , człony z jednomianem, dwumianem w mianowniku zawsze będą stabilne!* Nawet przy bardzo dużym K. Owszem, powstaną oscylacje ale zanikające!
* przy założeniu że współczynniki a0 i a1 są dodatnie. Ale tak zwykle jest w układach otwartych.
Rozdz. 17.3.2 Badanie członu trójinecyjnego w układzie otwartym

Rys. 17-12
Układy niestabilne mogą być nieruchome, gdy wejście x(t)=0, tak jak teoretycznie ołówek postawiony pionowo na stole. Dlatego ten i następne (zwłaszcza) układy będziemy wytrącać z równowagi sygnałem x(t)-„prztyczkiem”. Jest to krótki impuls o czasie trwania t=0.02 sek i amplitudzie 50. Jego pole ma wartość 1 i dlatego traktujemy go jako w miarę dokładne przybliżenie impulsu Diraca. Pamiętaj o jego dużej amplitudzie, zwłaszcza, że oscyloskop „obcina” tu y(t) na poziomach +6 i -6.
Wejście x(t) działa na trójinercyjny tylko przez krótki czas od 3 sek do 3.02 sek. W tym czasie w trójinercyjnym magazynowana jest energia od x(t), która potem „rozładowuje” się dając taki przebieg y(t) z maksimum dla ok. t=5sek.
Porównaj z odpowiedzią idealnego członu opóźniającego z Rys. 17-3.  Z trudem bo z trudem, ale widać pewną analogię. Tyle tylko, że y(t) zostało „rozmyte”. Po pewnym czasie t wyjście y(t) osiąga maksimum. Ten czas to takie „pseudoopóźnienie” To.
Analogia do członu opóźniającego jest trochę naciągana, ale mechanizmy powodujące niestabilność w członie idealnym opóźniającym i trójinercyjnym są w sprzężeniu zwrotnym podobne. Na przykład to, że zwiększanie wzmocnienia K powoduje niestabilność.
Rozdz. 17.3.3 Człon trójinercyjny w układzie zamkniętym K=3
Zamknijmy człon z Rys. 17-12 pętlą ujemnego sprzężenia zwrotnego.

Rys.17-13
Na wejście trójinercyjnego działa sygnał e(t)=x(t)-y(t). Na początku x(t) ma bardzo dużą amplitudę x(t)=50 ale działa bardzo krótko 0.02 sek. Potem cały czas x(t)=0 i dalszy wzrost y(t) do czasu osiągnięcia maksimum dla t=4.3 sek odbywa się głównie dzięki energii otrzymanej od x(t) w czasie 0.02 sek. Dlatego przebieg początkowy y(t) jest podobny do układu otwartego z Rys. 17-13. Podobny, ale nie do końca. Maksimum w układzie otwartym wypada trochę później tj. dla t=5 sek. Dlaczego?
W układzie otwartym na Rys.17-13 po czasie 3.02 sek sygnał x(t)=0. Sygnał wejściowy na G(s) jest zerowy i przebieg y(t) wynika tylko z rozładowywania się energii. Natomiast na Rys. 17-13 cały czas działa „siła hamująca” e(t)=x(t)-y(t)=-y(t)! Tego nie było na Rys. 17-12. Dlatego maksimum wystąpiło wcześniej tj. dla t=4.35 sek. Mało tego. „Hamowanie” -y(t) powoduje, że y(t) osiąga w 5.8 sek stan y(t)=0 i dalej pędzi w kierunku wartości ujemnych. Teraz „hamowanie” stara się znowu zawrócić y(t) do y(t)=0. I tak z kilkoma oscylacjami system wraca do stanu ustalonego y(t)=0.
Z badania członu opóźniającego wynika, że zwiększając K możemy spowodować niestabilność.
Spodziewamy się, że podobnie jest dla członu trójinercyjnego jako przedstawiciela obiektów ciągłych (czytaj „normalnych”). To zwiększmy wzmocnienie z K=3 na K=7.
Rozdz. 17.3.4 Człon trójinercyjny w układzie zamkniętym K=7
Transmitancja różni się od tej z Rys. 17-13 tylko  wzmocnieniem K=7

Rys. 17-14
Na wejście podawany jest ten sam impuls prostokątny („prawie dirac”) x(t).
Układ dłużej się buja, ale dalej jest stabilny. Większe bujanie spowodowało właśnie to większe K, które silniej pcha y(t) w kierunku y(t)=0.  Czyli większe przeregulowanie. To jeszcze zwiększmy wzmocnienie na K=10.035. Zaraz okaże się dlaczego akurat 10.035.
Rozdz.17.3.5 Człon trójinercyjny w układzie zamkniętym K=10.035

Rys.17-15
Układ jest na granicy stabilności. Dla członu opóźniającego było K=1, tu zaś K=10.035 a dla innego członu dynamicznego będzie jeszcze inna wartość. Kryterium stabilności jest bardziej skomplikowane, niż dla opóźniającego. Chyba to nie dziwi. Przecież trójinercyjny jest „trudniejszy” niż opóźniający. Teraz K=10.035 spowodowało, że kolejna amplituda ma taką samą wartość co poprzednia. Gdyby K było trochę mniejsze to zabrakłoby energii. Następna amplituda będzie trochę mniejsza. Gdy K będzie większe to amplitudy będą narastać. Sprawdźmy dla np. K=12.
Rozdz. 17.3.6 Człon trójinercyjny w układzie zamkniętym K=12

Rys.17-16
Wzmocnienie K=12 już jest takie, że każda kolejna amplituda dostaje większego kopa. Amplitudy narastają do nieskończoności.
Układ jest niestabilny.

Rozdz. 17.4 Człon trójinercyjny w układzie zamkniętym – skok jako sygnał wejściowy
17.4.1 Wstęp
Przy badaniu niestabilności wystarczyło „prztyknąć” impulsem diraca w człon trójinercyjny aby ewentualnie wyprowadzić go ze stanu równowagi y(t)=0. Gdy układ był stabilny–>Rys.17-13, Rys. 17.14, to wrócił do stanu równowagi y(t)=0. W przeciwnym przypadku powstały drgania o stałej amplitudzie–>Rys. 17.15 lub narastającej –>Rys. 17-16.
A jak się będzie zachowywał układ stabilny i niestabilny gdy sygnał wejściowy x(t) jest skokiem 1(t)?*
* ściślej, skokiem x(t)=1(t-3) bo opóźnionym o względem t=0 o 3 sek.
Rozdz. 17.4.2 Odpowiedź na skok układu stabilnego K=3

Rys.17-17
Klasyka. Sygnał y(t) dochodzi do stanu ustalonego y=0.75 wg. znanego do bólu wzoru.
Rozdz.17.4.3 Odpowiedź na skok układu niestabilnego K=12
Wydawałoby się że wzmocnienie Kz w stanie ustalonym nie ma sensu dla układu niestabilnego. Tak trochę, to jednak ma.

Rys. 17-18
Amplituda drgań zwiększa się do nieskończoności wokół składowej stałej y=0.923 wyznaczonej wg. znanego wzoru.