Wirujące Szeregi Fouriera
Rozdział 12. Szereg Fouriera klasycznie
Rozdział 12.1 Wstęp
Wzory związane z Szeregiem Fouriera przedstawiono na rys. 7.2 w rozdz.7. Bazowały na tym, że n-tą harmoniczną był podwojony wektor wskazujący n-ty środek ciężkości scn trajektorii F(njω0t)=f(t)*exp(njω0t). Ściślej, była to zespolona amplituda n-tej harmonicznej okresowej funkcji f(t).
Teraz przedstawię wzory w postaciach najczęściej spotykane w literaturze tzn.
-wersja zespolona z pulsacjami dodatnimi–>Rozdz. 12-6
-wersja trygonometryczna z pulsacjami dodatnimi–>Rozdz. 12-7
-wersja zespolona z pulsacjami dodatnimi i ujemnymi–>Rozdz. 12-8
-wersja trygonometryczna z pulsacjami dodatnimi i ujemnymi–>Rozdz. 12-9
Najczęściej wykłady z Szeregów Fouriera zaczynają się od wzorów trygonometrycznych z cosinusami i sinusami a dopiero potem przechodzi się do zespolonej wersji. U mnie jest odwrotnie i chyba bardziej intuicyjnie. Zaczynam od F(njω0t) ze środkami ciężkości scn, czyli w wersji zespolonej i kończę klasycznie-trygonometrycznie.
Rozdział 12.2 Jeszcze raz związek środka ciężkości scn trajektorii z n-tą harmoniczną
Wszystkie 4 wersje ze Wstępu wynikają oczywiście z n-tych środków ciężkości scn trajektorii na Rys. 7-2 rozdziału 7.2.
Przypomnę najważniejsze wzory, które mam dzieję są zrozumiałe. Przynajmniej intuicyjnie.
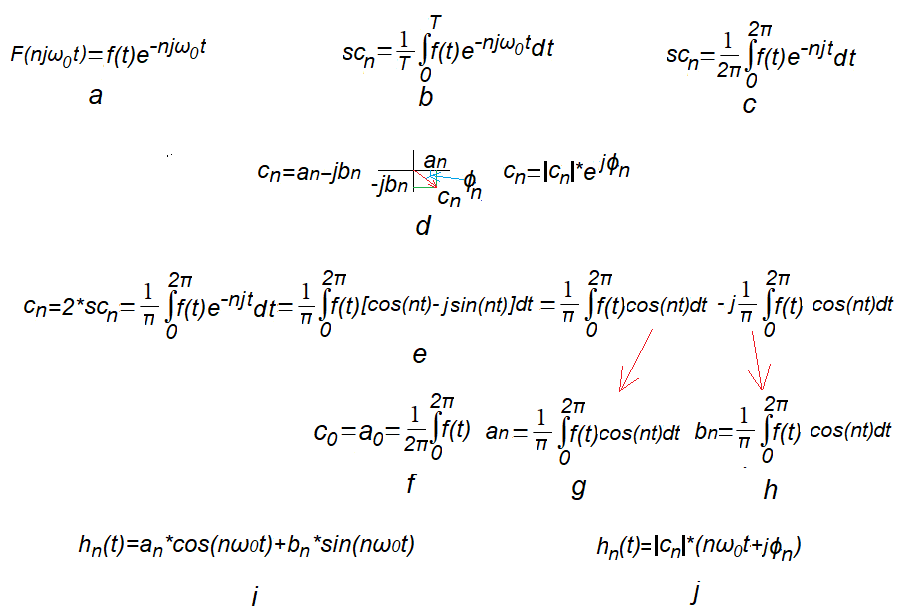
Rys. 12-1
Związek środka ciężkości scn trajektorii F(njω0t) z zespolonymi współczynnikami Fouriera c0, cn=an-jbn i harmonicznymi hn(t) funkcji f(t).
Rys. 12-1a
Trajektoria F(njω0t)
Rys. 12-1b
Wzór ogólny na środek ciężkości scn n-tej trajektorii F(njω0t) dla f(t) o dowolnej pulsacji ω0 lub okresie T.
Rys. 12-1c
Wygodniejszy wzór na scn trajektorii gdy ω0=1/sek (czyli T=2π sek).
Jest to prawie, bo z pewnym zastrzeżeniami, wzór ogólny–> patrz Rozdz. 7.6.
Rys. 12-1d
n-ty współczynnik Fouriera jako liczba zespolona w różnych wersjach
Rys. 12-1e
n-ty współczynnik Fouriera jako podwojony środek ciężkości scn n-tej trajektorii F(njω0t).
Pokazano, jak rozłożono współczynnik na składową cosinusoidalną i snusoidalną. Inaczej-na rzeczywistą i urojoną.
Rys.12-1f
Wzór na składową stałą czyli współczynnik c0=a0 szeregu Fouriera.
Rys. 12-1g
Wzór na składową an, czyli cosinusowa szeregu Fouriera. Czerwona strzałka pokazuje “pochodzenie”
Rys. 12-1h
Wzór na składową bn, czyli sinusową szeregu Fouriera. Czerwona strzałka pokazuje “pochodzenie”
Rys. 12-1i
n-ta harmoniczna hn(t) jako suma składowej cosinusoidalnej i sinusoidalnej.
Rys. 12-1j
n-ta harmoniczna hn(t) jako cosinus z przesunięciem fazowym ϕ. Moduł |cn| jest “pitagorasem” z an i bn.
Rozdział 12.3 Funkcja testowa f(t) do badania Szeregów Fouriera
Znajdziemy Szereg Fouriera dla:
f(t)=0.25+1cos(1t)+0.3sin(1t)+0.6cos(2t)-0.4sin(2t)+0.4cos(3t)+0.2sin(3t). Harmoniczne cosinusowe i sinusowe są widoczne. Wzory na Szereg Fouriera powinny je potwierdzić. Potem uogólnimy wzór na dowolną funkcję okresową f(t).
Rys. 12-2
f(t)=0.25+1cos(1t)+0.3sin(1t)+0.6cos(2t)-0.4sin(2t)+0.4cos(3t)+0.2sin(3t) o okresie pulsacji T=2π sek
c0=a0=+0.25 składowa stała
cn=an-jbn czyli
c1=1-j0.3 czyli a1=+1 i b1=+0.3
c2=0.6+j0.4 czyli a2=+0.6 i b2=-0.4
c3=0.4-j0.2 czyli a3=+0.4 i b3=+0.2
Rozdział 12.4 Suma cosinusów i sinusów jako wirujące wektory
Z rozdz. 2 Rys. 2-3 wynika że wirujący wektor exp(1j1t):
-jest dwuwymiarowym modelem funkcji f(t)=cos(1t)
-rzut wirującego wektora exp(1j1t) na oś rzeczywistą Re z jest funkcją f(t)=cos(1t)
Analogicznie z rozdz. 2 Rys. 2-4 wynika że wirujący wektor -j*exp(1j1t):
-jest dwuwymiarowym modelem funkcji f(t)=sin(1t)
-rzut wirującego wektora exp(-1j1t) na oś rzeczywistą Re z jest funkcją f(t)=sin(1t)
Powyższe można uogólnić np. na trzy wirujące z prędkościami 1/sek, 2/sek i 3/sek wektory z Rys. 12-3c i odpowiednią kombinację liniową cosinusów i sinusów

Rys. 12-3
a. Funkcja f(t) jako kombinacja liniowa cos(1t),cos(2t),cos(3t) i sin(1t),sin(2t),sin(3t) oraz stałej a0.
b. Funkcja f(t) jako rzut wirujących wektorów c1*exp(1j1t), c2*exp(2j1t) i c3*exp(3j1t) oraz stałej a0 na oś rzeczywistą czyli f(t)=Re{a0+…}
c. Wirujące wektory ze stanami początkowymi c1=a1-jb1, c2=a2-jb2 i c3=a3-jb3 oraz stała a0 są modelem funkcji f(t) z Rys a. Skojarz parametry an i bn ze współczynnikami an przy cosinusach i bn przy sinusach na Rys. a.
d. Konkretny przypadek funkcji gdy f(t) jest z Rys. 12-2
e. Wirujące wektory dla konkretnej funkcji z Rys. 12-2 jako jej model.
Rys.12-4
f(t)=Re{0.25+1cos(1t)+0.3sin(1t)+0.6cos(2t)-0.4sin(2t)+0.4cos(3t)+0.5sin(3t)
Interpretacja animacji trwającej T=2πsek
+0.25 wektor nieruchomy czyli stała a0=+0.25
+(1-0.3j)exp(1j1t) wektor pierwszej harmonicznej obracający się z prędkością 1ω0=1/sek. W czasie T=2πsek wykona 1 obrót
+(0.6+0.4j)exp(2j1t) wektor drugiej harmonicznej obracający się z prędkością 2ω0=2/sek. W czasie T=2πsek wykona 2 obroty
+(0.4-0.2j)exp(3j1t) wektor trzeciej harmonicznej obracający się z prędkością 3ω0=3/sek. W czasie T=2πsek wykona 3 obroty
A jakie będą rzuty tych wektorów w czasie? Wróć na chwilę do Rozdz. 2.6 gdzie dowiesz się ,że:
Re (a-jb)*exp(jω0t)=a*cos(ω0t)+b*sin(ω0t).
Czyli
Re (1-0.3j)exp(1j1t)=1cos(1t)+0.3sin(1t)
Re (0.6+0.4j)exp(2j1t)=0.6cos(2t)-0.4sin(2t)
Re (0.4-0.2j)exp(3j1t)=0.4cos(3t)+0.2sin(3t)
oraz
Re {+0.25}=+0.25 co jest oczywistą oczywistością
Czyli suma rzutów wirujących wektorów na oś Re jest funkcją f(t) z Rys. 12-2!
Albo, co na jedno wychodzi
Rzut rzut sumy wirujących wektorów na oś Re jest funkcją f(t) z Rys. 12-2!
Inaczej
Część rzeczywista czyli Re sumy sumy wszystkich wirujących wektorów na oś Re jest funkcją f(t) z Rys. 12-2!
Rozdz. 12.5 Wirujący wektor jako model funkcji f(t)=an*cos(n*ω0t)+bn*sin(n*ω0t)
Gdy np. n=1 i ω0=1/sek to a1=1, b1=-0.3 czyli f(t)=1*cos(1t)+0.3*sin(1t)
Rys. 12-5
Wirujące wektory jako model funkcji f(t)=1cos(1t)+0.3sin(1t)
Rys. 12-5.1
Pojedynczy wirujący wektor jako model f(t)
a. Wirujący wektor +(1-0.3j)*exp(1t)
b. f(t)=Re{(1-0.3j)exp(1j1t)}
Inaczej rzut wirującego 1-0.3j)exp(1j1t) na oś rzeczywistą Re z jest funkcją f(t)
Rys. 12-5.2
Para wirujących wektorów jako model f(t)
a. Wirujący wektor+(0.5-0.15j)*exp(1t). Jest to połowa wirującego wektora z Rys. 12-5.1a
b. Wirujący w przeciwnym kierunku wektor +(0.5+0.15j)*exp(-1j1t).
Jako liczba zespolona jest on w każdej chwili liczbą sprzężoną względem wirującego wektora a.
Uwaga
Liczby zespolone np. z=5+3j oraz z*=5-3j są tzw. liczbami sprzężonymi.
Zauważ, że z* jest lustrzanym odbiciem względem z, gdy “lustrem” jest oś rzeczywista Re z.
c. f(t)=(0.5-0.15j)*exp(1t)+(0.5+0.15j)*exp(-1j1t)
Innymi słowy
Suma (zespolona albo wektorowa) przeciwnie wirujących wektorów a oraz b jest funkcją rzeczywistą f(t). Rzeczywiście, wektor c porusza się identycznie jak wektor Rys. 12-5.1b. Zauważ, że funkcji f(t) nie musimy wyłuskiwać jako część rzeczywistą liczby zespolonej!
Wnioski
1. Obydwa modele tj. pojedynczy wirujący wektor oraz para wirujących wektorów opisują tą samą funkcję f(t)czyli
f(t)=an*cos(n*ω0t)+bn*sin(n*ω0t)
2. Pojedyncze wirujące wektory zastosowano w Rozdziale 12.6 Zespolony Szereg Fouriera z pulsacjami dodatnimi
3. Pary wirujących wektorów zastosowano w Rozdziale 12.8 Zespolony Szereg Fouriera z pulsacjami dodatnimi i ujemnymi
Rozdział 12.6 Zespolony Szereg Fouriera z pulsacjami dodatnimi
Jest to uogólniony wzór na pojedyncze wirujące wektory z Rys. 12-3e oraz animacji Rys. 12-4 dla n=∞
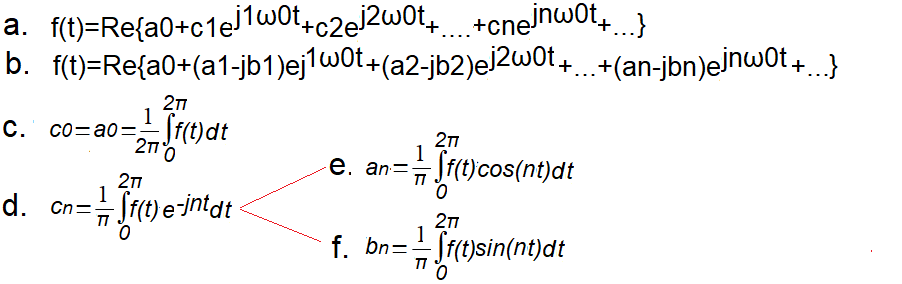
Rys. 12-6
Zespolony Szereg Fouriera z pulsacjami dodatnimi
Dowolna (prawie, ale nie wnikajmy w szczegóły) funkcja okresowa f(t) może być przedstawiona jako nieskończony szereg wirujących wektorów plus składowa stała co.
a. Pojedyncze wirujące wektory z amplitudami zespolonymi c1, c2 …cn ze składową stałą c0. Rzut tych wektorów na oś rzeczywistą Re z (czyli Re{...} jest właśnie funkcją f(t). Prędkość ω0 np. ω0=1/sek odpowiada pulsacji funkcji okresowej f(t).
b. Jak wyżej, tylko amplitudy zespolone jako c0=a0, c1=a1-jb1, c2=a2-jb2,…cn=an-jbn
Np. dla animacji z Rys. 12-4
a0=+0.25
c1=a1-jb1=1-j0.3–>a1=1 b1=+0.3
c2=a2-jb2=0.6+j0.4–>a2=0.6 b2=-0.4
c3=a3-jb3=0.4-0.2j–>a3=0.4 b3=+0.2
c. Wzór na składową stałą c0=a0 funkcji okresowej f(t).
d. Wzór na współczynniki zespolone cn funkcji okresowej f(t), inaczej na amplitudy zespolone cn dla n-tych harmonicznych.
Jest to podwojony środek ciężkości scn wirującej trajektorii z prędkością n*ω0.
Możesz to przyjąć na słowo honoru, ale powinny Cię przekonać
– rozdz. 7 teoria
– rozdz. 11“Sprawdzenie wzorów…”
Radzę przeczytać komentarz do Rys. 12-1c.
e. składowa rzeczywista, amplitudy zespolonej an, inaczej cosinusoidalna
f. składowa urojona, amplitudy zespolonej bn, inaczej sinusoidalna
Zauważ, że ω0 czyli pulsacja podstawowa funkcji f(t) pojawiają się tylko we wzorach a i b. Nie ma ich natomiast we wzorach d, e, f. Współczynniki an, bn np. fali prostokątnej zależą tylko od jej amplitudy i stopnia wypełnienia. Nie zależą natomiast od jej pulsacji, częstotliwości lub okresu. Pisałem o tym w rozdziale 7.6.
Rozdział 12.7 Trygonometryczny Szereg Fouriera z pulsacjami dodatnimi
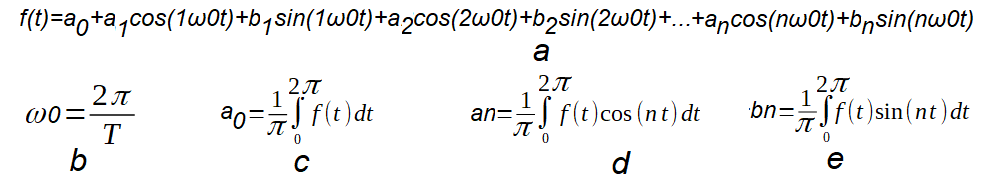
Rys. 12-7
Trygonometryczny Szereg Fouriera z pulsacjami dodatnimi
a. Szereg Fouriera z pulsacjami dodatnimi.
Wynika bezpośrednio ze wzorów
– Rys. 12-6b gdzie f(t) jest częścią rzeczywistą funkcji zespolonej w klamrach Re{…}
Inaczej, funkcja zespolona w klamrach jest sumą wirujących wektorów (an-jbn) i rzut tej sumy jest właśnie funkcją f(t).
b. Pulsacja pierwszej harmonicznej ω0 gdzie T jest okresem funkcji f(t)
c. Składowa stała a0
d. Składowa n-ta cosinusoidalna an
e. Składowa n-ta sinusoidalna bn
Rozdział 12.8 Zespolony Szereg Fouriera z pulsacjami dodatnimi i ujemnymi
Szereg Fouriera bazuje na środkach ciężkości scn trajektorii F(njω0t) wirujących z prędkościami nω0. Są one amplitudami zespolonymi dla tych pulsacji. Poprzednio tj. w rozdz. 12.6 i 12.7 były podwojonymi amplitudami.
Rozdział 12.8.1 Zespolony Szereg Fouriera z pulsacjami dodatnimi i ujemnymi dla funkcji testowej f(t).
Jeżeli we wzorze Rys. 12-3e i w animacji Rys. 12-4 każdy pojedynczy wirujący wektor zastąpimy parą wirujących wektorów, to otrzymamy poniższą animację. Np. pojedynczy wirujący wektor Rys. 12-5.1 został zastąpiony parą wirujących wektorów Rys. 12-5.2.
Rys. 12-8
f(t)=(0.2+0.1j)*exp(-3jt)+(0.3-0.2j)*exp(-2jt)+(0.5+0.15j)*exp(-1jt)+0.25+(0.5-0.15j)*exp(+1jt)+(0.3+0.2j)*exp(+2jt)+(0.2-0.1j)*exp(-1jt).
Trzy lewe wektory wirują przeciwnie niż trzy prawe i tworzą 3 pary przeciwnie wirujących wektorów. Środkowy wektor +0.25 nie wiruje i jest składową stałą a0 funkcji f(t). Funkcja f(t) jest sumą powyższych wirujących wektorów. W odróżnieniu od Rys. 12-4 (z tą samą f(t)!), nie trzeba używać operacji wyłuskiwania części rzeczywistej f(t). Zamiast f(t)=Re{…} piszemy po prostu f(t)=…
Ktoś może się zastanawiać. Po prawej stronie równania wirujące wektory, a po lewej funkcja rzeczywista f(t). Tak jakby po prawej były gruszki a po lewej krowy. To zsumujmy prawe wektory (łącznie z wektorem stałym a0=+0.25 ściślej a0=(0, +0.25). Otrzymamy lewy pulsujący wektor ze składową stałą a0=+0.25 będący właśnie f(t)! Wszędzie gruszki.
Rys. 12-9
Pulsujący wektor jako f(t) jako suma wirujących wektorów z Rys. 12-8
a. Pulsujący na Re z osi rzeczywistej wektor ze składową stałą a0
b. Funkcja f(t) opisująca ruch pulsującego wektora na osi Re z
Jest to dokładnie funkcja z Rys. 12-2. Po lewej stronie równania Rys. 12-4 też jest ta sama funkcja f(t), ale po prawej jest rzut sumy wirujących wektorów, czyli Re z {…}.
Wróćmy jeszcze raz do tematu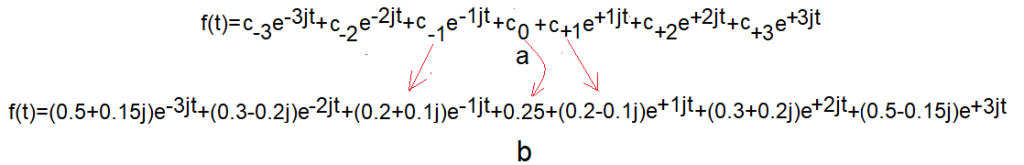
Rys. 12-10
a. Zespolony Szereg Fouriera z pulsacjami dodatnimi i ujemnymi współczynnikami c(n) dla n=0…+∞.
b. Przykład Zespolonego Szeregu Fouriera z pulsacjami dodatnimi i ujemnymi i z konkretnymi zespolonymi współczynnikami c(n) dla n=0,1,2,3.
np. c(-1)=0.2+0.1j, c(0)=+0.25, c(1)=0.2-0.1j
Zauważ, że np. c(-1) jest liczbą sprzężoną do c(1)
Współczynniki a(n),b(n) dla n dodatnich i ujemnych otrzymaliśmy bezpośrednio ze wzoru 12-10b. Nie trzeba było ich (chociaż można) obliczać.
Rozdział 12.8.2 Zespolony Szereg Fouriera z pulsacjami dodatnimi i ujemnymi dla dowolnej funkcji f(t).
Czyli wzór który otrzymamy uogólniając Rys. 12-10a. Przy okazji wyjdzie fajna rzecz. Szereg Fouriera z pulsacjami tylko dodatnimi ma zespolone amplitudy harmonicznych, są podwojonymi środkami ciężkości scn wirujących trajektorii F(njω0). Teraz już wiemy dlaczego poprzednio scn były podwojone. Bo obsługiwały 2 razy mniejszą liczbę “cięższych” harmonicznych.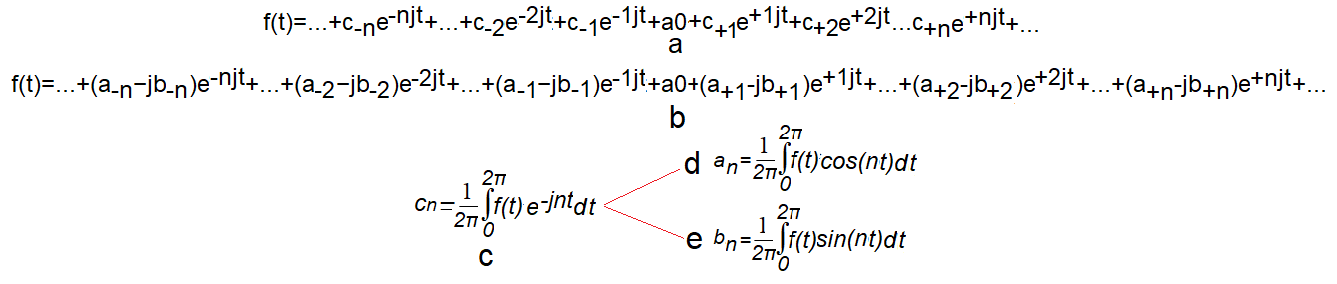
Rys. 12-11
a. Zespolony Szereg Fouriera z pulsacjami dodatnimi i ujemnymi ze współczynnikami cn
b. Zespolony Szereg Fouriera z pulsacjami dodatnimi i ujemnymi ze szczegółowymi współczynnikami cn
Zauważ, że każdemu współczynnikowi Fouriera c(+n)=a(n)-jb(n) przy dodatnich pulsacjach nω0 odpowiada współczynnikowi Fouriera c(-n)=a(-n)+jb(-n). Współczynniki te są względem siebie liczbami sprzężonymi c(+n)=c(-n)*
c. wzór na zespolony współczynnik c(n) Fouriera. Jest 2 razy mniejszy niż odpowiedni współczynnik c(n) na Szereg Fouriera na Rys. 12-6d
d. wzór na a(n)=a(-n)
e. wzór na b(n)=-b(-n)
Zauważ, że współczynniki c(n), a(n) i b(n) są 2 razy mniejsze od analogicznych c(n), a(n) i b(n) rozdz. 12.6
Rozdział 12.10 Trygonometryczny Szereg Fouriera z pulsacjami dodatnimi i ujemnymi.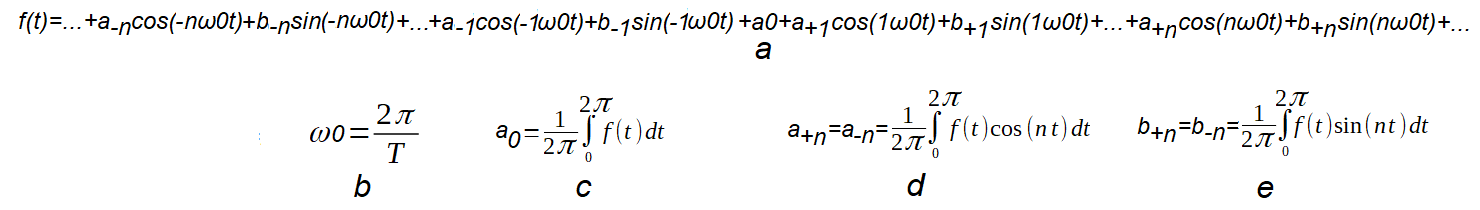
Rys. 12-12
Trygonometryczny Szereg Fouriera z pulsacjami dodatnimi i ujemnymi
a. Szereg Fouriera z pulsacjami dodatnimi.
Wynika bezpośrednio ze wzorów
– Rys. 12-11b gdzie f(t) jest częścią rzeczywistą funkcji zespolonej w klamrach Re{…}
– Rys. 2-9d rozdz. 2
b. Pulsacja pierwszej harmonicznej ω0 gdzie To jest okresem funkcji f(t)
c. Składowa stała a0
d. wzór na a(n)=a(-n)
e. wzór na b(n)=-b(-n)
Zauważ, że współczynniki a(n) i b(n) są 2 razy mniejsze od analogicznych a(n) i b(n) rozdz. 12.7
Rozdział 12.11 Trygonometryczny Szereg Fouriera z pulsacjami dodatnimi i ujemnymi dla dowolnego T.
Często współczynniki an, bn nie zależą od okresu T funkcji f(t). Np. dla fali prostokątnej o wypełnieniu 50% są takie same dla okresu T=1sek i T=3sek. Wtedy możemy założyć, że Tπ=2π jak na Rys. 12-12. Zawsze to jeden parametr mniej i łatwiejsze rachunki. Patrz rozdz. 7.7. Ale nie zawsze tak jest. Przekonasz się o tym w artykule “Transformata Fouriera” rozdz. 3.3. Wtedy stosujemy wzór z “ogólnym T“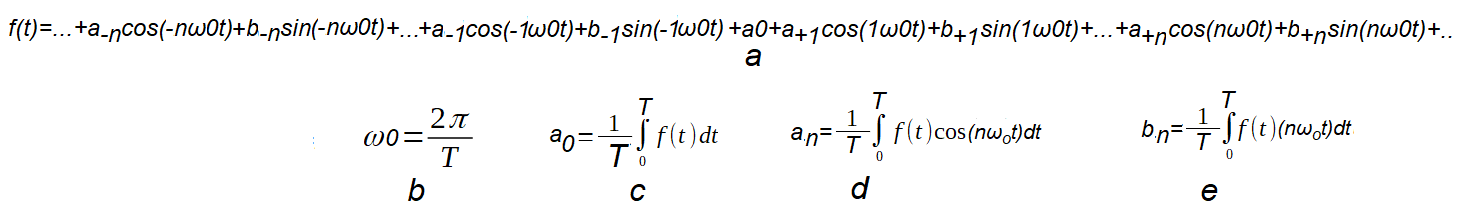
Rys. 12-13
Trygonometryczny Szereg Fouriera z pulsacjami dodatnimi i ujemnymi dla dowolnego T.
Dla funkcji okresowych całki nie zależą też od przedziału całkowania. Są takie same dla 0…T, –T/2…+T/2 czy też dla -T/4…+T3/4. Wtedy możemy zastosować np. poniższy wzór.
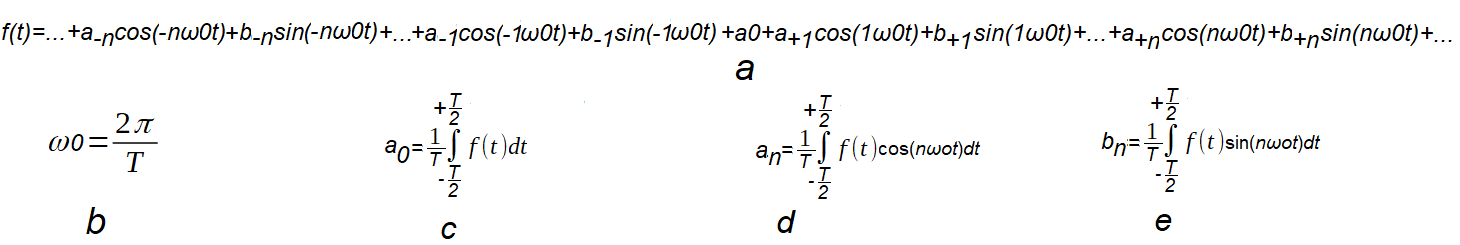
Rys. 12-14
Trygonometryczny Szereg Fouriera z pulsacjami dodatnimi i ujemnymi dla przedziału –T/2…+T/2.
Taki przedział może nam czasami ułatwić rachunki.
