Rys.2-1
Wykres f(x)=2x+1 i jak go wykonać programem Geogebra
Po wciśnięciu “trójkącika” przycisku video zobaczysz kolejne etapy powstawania wykresu. 
1. Wpisałem do dowolnej wyszukiwarki, np. Google, tekstu “geogebra.org”. Bez cudzysłowów oczywiście.
2. Wybrałem  link do Geogebry
3. Kliknąłem przycisk “Uruchom Kalkulator”
4. Jestem w podaplikacji “Wykresy”. Mógłbym już tworzyć wykres f(x)=2x+1, ale pokażę pozostałe podaplikacje Rys.1-2.
5. Z listy rozwijającej się wybrałem podaplikacje “Wykresy”, “Grafika 3D“,”Geometria”, “CAS“, “Prawdopodobieństwo”, czyli różne działy matematyki.  Najczęściej wybierane są “Wykresy” dotyczące funkcji jednej zmiennej f(x).  Grafika 3D  to funkcje 2 zmiennych f(x,y). CAS jest jakby wzbogaconą wersją “Wykresy” np. o rachunek różniczkowy. “Prawdopodobieństwo”-sama nazwa wskazuje.
6. W końcu wróciłem do “Wykresy”. Tu w okienku “Wprowadź…” wpisaliśmy 2x+1 i wcisnąłem Enter!, Program sam coś dopisał i powstał opis wykreu f(x)=2x+1. Jak jesteś Niewiernym Tomaszem, to sprawdź. Np. f(2)=5. Zgadza się. Punkt (2,5) leży na wykresie.
Uwaga:
Animacja jest trochę niewyraźna. Może jej powiększenie trochę pomoże?  Wciśnij kwadrat z czarnym rombem w prawym końcu magnetowidu.

Rys. 2-2
Podaplikacje Geogebry.

Rozdz. 2.2 Obróbka wykresu f(x)=2x+1.
Najważniejsze już zrobiłeś. Umiesz narysować wykres f(x)=2x+1. To już wystarczy, żeby badać inne funkcje np. f(x)=x² lub sin(x)…
Ale chciałbyś panować nad wykresem. Napisać jaka to funkcja, wybrać kolor linii, typ linii-ciągła lub przerywana, grubość itd.

Rys.2-3
Stan końcowy animacji z nastawami wykresu.
1. Klikam przycisk “Algebra”, który włącza/wyłącza pasek wpisywania funkcji.
2. Wpisuję funkcję 2x+1 +Enter. Program automatycznie dopisze  f(x)=.
3. Klikam 3 pionowe kropki. Otwiera się rozwijana lista czegoś tam, wybieram “Ustawienia”.
4. Otwiera się okno “Ustawienia” z zakładką “Podstawowe”. Pozostałe zakładki są nieaktywne.
5. W zakładce “Ustawienia”możeny zmienić 
     – nazwę funkcji-tu f 
     – definicję funkcji- tu 2x+1
     – polecam zaptaszkować okienka “Pokaż obiekt”, “Pokaż etykietę”, “Posadź obiekt”.
     – w okienku “Nazwa” wybrałem  “Nazwa i wartość”.
5. W zakładce “Kolor” wybieram kolor czerwony.
6. W zakładce “Styl” wybieram linię ciągłą i grubość 3. Możesz wybrać linię przerywaną i inną grubość.
7. Przesuwam etykietę i wartość tj napis f(x)=2x+1 w bardziej widoczne miejsce obok wykresu.
Polecam pobawić się nastawami, także innymi. Może będzie lepiej.
Animacja powinna wystarczyć. Dla pełnej jasności dodam jeszcze rysunek z jednocześnie otwartymi  oknami, które pojawiły się w animacji.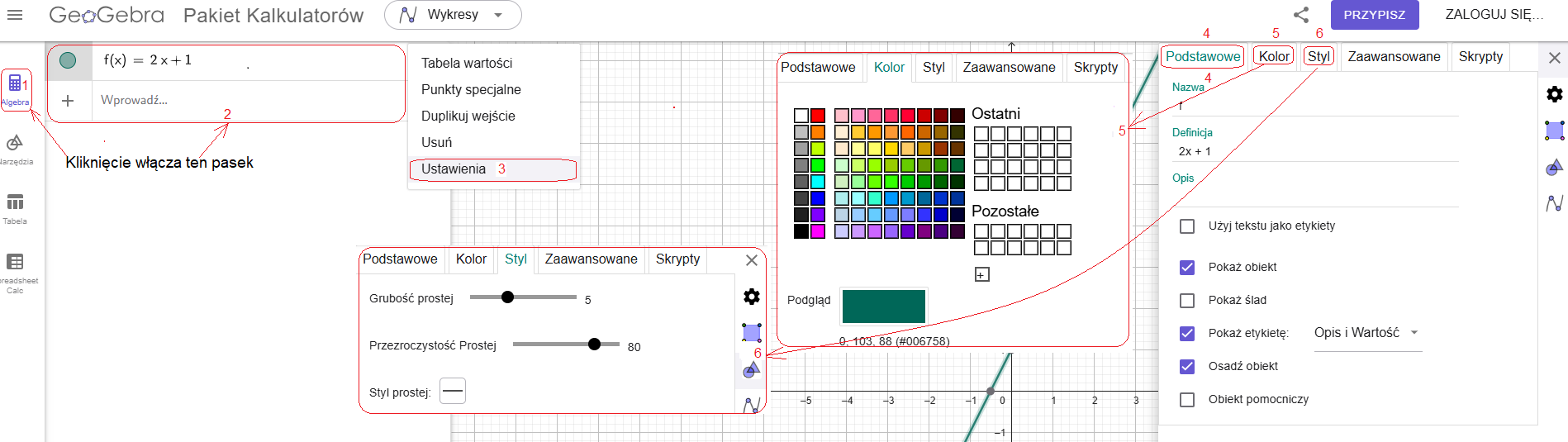

Rys. 2-4
Okna nastaw wykresu, które pojawiły się w animacji Rys. 1-3

Rozdz. 2.3 Co by tu jeszcze ustawić?
Na animacji pokażę jak:
1. Zrobić wykres bez siatki
2. Zrobić wykres z siatką główną (siatka “rzadka”)
3. Zrobić z siatką główną i pomocniczą
4. Powiększyć i zmniejszyć wykres
5. Przesunąć wykres  (lewym przyciskiem myszy)
6. Powrócić do wykresu początkowego 

Rys.2-5
Dalsza obróbka wykresu f(x)=2x+1.
Dobrze, gdy to co jest najważniejsze, byłoby mniej więcej w środku ekranu. Także siatka powinna być optymalne. Nie za duża, nie za mała.
Rozpoznaj na animacji operacje 1…6.

Rozdz. 2.4 Układ równań
Geogebra, ściślej jej podaplikacja “Wykresy” z której korzystamy, bez problemu rysuje układy 2 równań. 

Rys.2-6
Układ 2 równań 
x+y=4
2x-y=-1
Po wpisaniu x+y=4 automatycznie została dopisana nazwa równania Eq1  i analogicznie dla drugiego Eq2. Ustawiałem tylko to co konieczne. Kolorki, grubości linii itd. już sobie darowałem. Natomiast wybrałem opcję etykiety “nazwa i wartość” Dzięki temu proste mają nazwy Eq1: x+y=4 i Eq2:2x-y=-1. Znakomicie ułatwia to analizę układu 2 równań. Akurat tu nie ma to znaczenia, ale przy bardziej skomplikowanych przypadkach już tak. 
Z przecięcia się prostych wynika rozwiązanie układu równań x=1 i y=3. Sprawdź.

Rozdz. 2.5 Wykres funkcji f(x)=x³-1.5x

Rys. 2-7
f(x)=x³-1.5x
Przypominam, że wyrażenie x³ piszemy tak–>x^3. 
Etykietę f(x)=x³-1.5x zasłania symbol magnetowidu. Ale widać ją przez chwilę w czasie animacji.

Rozdz. 2.6 Wykres funkcji f(x)=xsin(x)

Rys. 2-8
f(x)=xsin(x)
Etykieta z nazwą f(x)=xsin(x) w górnym rogu.
Zwróć uwagę jak zmieniam wzmocnienie wykresu, żeby był większy zakres.

Rozdz. 2.7 Jak zapisać, pobrać i wyczyścić wykres?
Pokażę jak pobrać plik Test z wykresem , obejrzeć go i wyczyścić,  stworzyć nowy wykres i zapisać go jako Test1. Pliki będą zapisane na komputerze. Można go także gdzieś w Internecie, ale tym się na razie nie zajmujemy.

Rys.2-9
Jak zapisać, pobrać i wyczyścić wykres?
Uwaga  pliki Test i Test1 są już gdzieś zapisane na komputerze. 
Animacja pokaże:
1. Pobranie pliku Test
2. Obejrzenie go jako wykres x²
3. Wyczyszczenie ekranu z wykresem x²
4. Stworzenie wykresu (x+3)(x-2)
5. Zapisanie go gdzieś jako Test1. Ten plik już istniał, dlatego został tylko zmodyfikowany. Można go zapisać oczywiście jako nowy plik pod nową nazwą