Wirujące Szeregi Fouriera
Rozdział 9 Szereg Fouriera fali prostokątnej nieparzystej.
Rozdział 9.1 Wstęp
Jest to fala z poprzedniego rozdziału przesunięta w prawo, (czyli opóźniona) o ćwierć okresu (czyli o 90° albo o π/2). I tak jak pierwszą harmoniczną poprzedniej był cosinus tak tej będzie sinus. Jest to przykład funkcji nieparzystej.
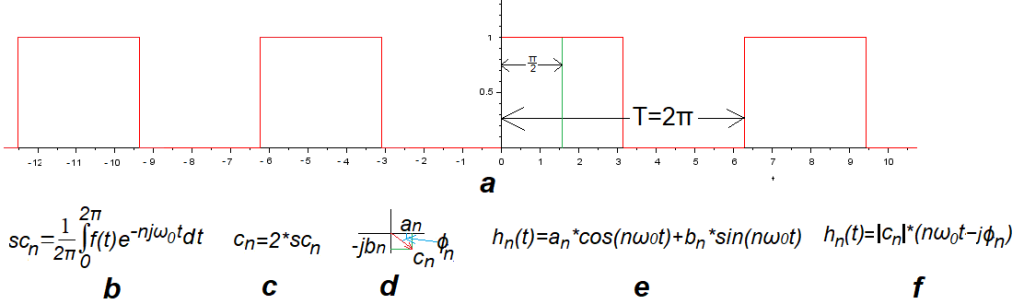
Rys. 9-1
Fala prostokątna nieparzysta f(t) A=1, ω=1/sek i ϕ=-π/2.
Parametr ϕ=-π/2 fali nieparzystej oznacza, że jest opóźniona o π/2 względem parzystej z poprzedniego rozdziału. Podobnie jak sinus jest opóźniony o π/2 względem cosinusa. W następnych punktach będziemy analizować trajektorie F(n*jω0t) i wykresy czasowe tej fali prostokątnej dla n=0…8.
Rozdział 9.2 Fala prostokątna nieparzysta f(t) i jej trajektoria F(njω0t) dla n=0 czyli F(0j1t)
Rys.9-2
Trajektoria F(0j1) funkcji f(t) fali prostokątnej nieparzystej, czyli o parametrach:
A=1-amplltuda
ω0=1/sek-pulsacja odpowiadająca okresowi T=2πsek≈6.28sek.
ϕ=-π/2
50%-wypełnienie
Rys.9-2a
Trajektoria F(0j1t) odpowiadająca trajektorii F(njω0t) dla n=0 i ω0=1/sek.
Nieruchoma płaszczyzna Z, gdzie na osi rzeczywistej Re Z wektor zmienia się wg. funkcji f(t) pokazanej na Rys.9-2b.
Rys.9-2b
Wykres czasowy f(t) fali prostokątnej nieparzystej.
Zauważ, że przebieg rozpoczyna się na początku okresu. Podobnie jak funkcja sinus. Obydwie animacje z Rys. a i b opisują to samo. Odczytaj parametry A,ω0,ϕ i wypełnienie.
W następnych podrozdziałach płaszczyzna Z zacznie obracać się z prędkościami ω= -nω0, czyli z prędkościami -1/sek,-2/sek…-8/sek. Koniec wektora będzie rysował trajektorie F(njω0). Z nich odczytamy harmoniczne dla pulsacji nω0.
Rozdział 9.3 Pierwsza harmoniczna fali prostokątnej nieparzystej h1(t) =b1*sin(1t).
Rozdział 9.3.1 Trajektoria F(njω0t) fali prostokątnej nieparzystej dla n=1 i ω0=1/sek, czyli F(1j1t).
Rys. 9-3
Trajektoria F(1j1t) fali prostokątnej nieparzystej
Rys.9-3a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-1/sek wokół punktu (0,0) w czasie T=2π sek i wykona 1 obrót.
Rys.9-3b
Trajektoria F(1j1t)=f(t)*exp(-1j1t) jako wirujący wektor modulowany funkcją f(t). Funkcja f(t) jest falą prostokątną z Rys.9-2b.
Płaszczyzna Z z Rys.9-2a zacznie się obracać z prędkością ω=-1/sek. W ten sposób powstanie wirujący wektor F(1j1t)=f(t)*exp(-1j1t). Płaszczyzna Z wykona 1 obrót, ale promień R=1 tylko 1 “półobrót”.
Rys.9-3c
Trajektoria F(1j1t) jako półokrąg rysowany przez koniec wektora z Rys.8-3b.
W czasie 1 obrotu płaszczyzny Z, czyli o kąt 0…2π wszystkie wektory są sumowane wektorowo i obliczana jest ich średnia w okresie T=2π sek. Będzie nim wektor, inaczej punkt sc1=(0,-1/π)=0-1j/π=-1j/π.
Rozdział 9.3.2 Pierwsza harmoniczna na tle fali prostokątnej nieparzystej czyli c0+h1(t) albo inaczej pierwsze przybliżenie fali prostokątnej nieparzystej.
Wg Rys. 8-1c
Składowa stała c0 to średnia w okresie T=2π czyli c0=a0=0.5.
Także c1 jest amplitudą zespoloną pierwszej harmonicznej
c1=2*sc1=(0,-2/π)=0-j2/π=-j2/π czyli a1=0 i b1=-2/π
Wg Rys. 8-1e
h1(t)=(2/π)*sin(1t)≈0.637sin(1t)
Rys.9-4
S1(t)=0.5+h1(t)=(2/π)*sin(1t) czyli pierwsza harmoniczna ze składową stałą c0 na tle fali prostokątnej.
Jest to także pierwsze przybliżenie naszej fali prostokątnej.
Rozdział 9.4 Druga harmoniczna fali prostokątnej nieparzystej, a właściwie jej brak bo c2=0 –>h2(t)=b2*sin(2t)=0.
Rozdział 9.4.1 Trajektoria F(njω0t) fali prostokątnej nieparzystej dla n=2 i ω0=1/sek, czyli F(2j1t).
Płaszczyzna Z obraca się z prędkością ω=-2/sek
Rys.9-5
Trajektoria F(2j1t) fali prostokątnej nieparzystej
Rys.9-5a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-2/sek wokół punktu (0,0) i wykona 2 obroty w czasie T=2π sek.
Rys.9-5b
Trajektoria F(2j1t)=f(t)*exp(-2j1t) jako wirujący wektor modulowany funkcją f(t). Wykona 1 obrót w pierwszym półokresie T/2=1π/sek i 0 obrotów drugim półokresie. Parametr sc2=0 jako średnia wartość T=2π sek jest oczywisty.
Rys.9-5c
Trajektoria F(2j1t) jako okrąg rysowany przez koniec wektora z Rys.9-5b.
Wniosek
sc2=0 i dlatego harmoniczna dla ω=2/sek nie istnieje.
Rozdział 9.5 Trzecia harmoniczna fali prostokątnej nieparzystej h3(t) =b3*sin(3t).
Rozdział 9.5.1 Trajektoria F(njω0t) fali prostokątnej nieparzystej dla n=3 i ω0=1/sek, czyli F(3j1t).
Płaszczyzna Z obraca się z prędkością ω=-3/sek
Rys.9-6
Trajektoria F(3j1t) fali prostokątnej nieparzystej
Rys.9-6a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-3/sek wokół punktu (0,0) i wykona 3 obroty w czasie T=2π sek.
Rys.9-6b
Trajektoria F(3j1t)=f(t)*exp(-3j1t) jako wirujący wektor modulowany funkcją f(t).
Wykona 1.5 obrotu w pierwszym półokresie T/2=1π/sek i 0 obrotów w drugim półokresie. W okresie T=2π sek promień R=1 dłużej przebywa na dolnej półpłaszczyźnie niż na górnej. Dlatego jego średnia wartość jako wektor będzie sc3=(0,-1/3π)=-1j/3π a nie sc3=(0,0) jak np. na Rys.9-5c
Rys.9-6c
Trajektoria F(3j1t) jako okrąg rysowany przez koniec wektora z Rys.9-6b.
Środek ciężkości sc3=(0,-1/3π) wynika z sumowania wektorów na Rys.9-6b i ich średniej w w czasie T=2π sek, gdy wykonane są 3 obroty płaszczyzny Z. Dolny półokrąg jest 2 razy rysowany, a górny tylko 1 raz. Tak jakby dolny półokrąg był 2 razy “cięższy”.
Rozdział 9.5.2 Trzecia harmoniczna na tle fali prostokątnej nieparzystej czyli c0+h3(t).
Wg Rys. 8-1c z rozdz. 8
c3 jest amplitudą zespoloną trzeciej harmonicznej
c3=2*sc3=(0,-2/3π) czyli a3=0 i b3=-2/3π
Wg Rys. 8-1e
h3(t)=(2/3π)*sin(3t)≈0.212sin(3t)
Rys.9-7
co+h3(t)=0.5+(2/3π)*sin(3t) czyli trzecia harmoniczna ze składową stałą c0 na tle fali prostokątnej.
Rozdział 9.5.3 Trzecie przybliżenie fali prostokątnej nieparzystej czyli S3(t)=c0+h1(t)+h3(t).
Rys.9-8
S3(t)=c0+h1(t)+h3(t)=0.5+(2/π)*sin(1t)+(2/3π)*sin(3t)
Trzecie przybliżenie jest bardziej podobne do fali prostokątnej niż pierwsze z Rys.9-4
Rozdział 9.6 Czwarta harmoniczna fali prostokątnej nieparzystej, a właściwie jej brak bo c4=0 –>h4(t)=c4*sin(4t)=0.
Rozdział 8.6.1 Trajektoria F(njω0t) fali prostokątnej nieparzystej dla n=4 i ω0=1/sek, czyli F(4j1t).
Płaszczyzna Z obraca się z prędkością ω=-4/sek
Rys.9-9
Trajektoria F(4j1t) fali prostokątnej parzystej
Rys.9-9a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-4/sek wokół punktu (0,0) i wykona 4 obroty w czasie T=2π sek.
Rys.9-9b
Trajektoria F(4j1t)=f(t)*exp(-4j1t) jako wirujący wektor modulowany funkcją f(t). Wykona 2 obroty w pierwszym półokresie T/2=1π/sek i 0 obrotów w drugim półokresie. Parametr sc4=0 jako średnia wartość T=2π sek jest oczywisty.
Rys.9-9c
Trajektoria F(4j1t) jako okrąg rysowany przez koniec wektora z Rys.9-9b.
sc4=0
Wniosek
sc4=0 i dlatego harmoniczna dla ω=4/sek nie istnieje.
Rozdział 9.7 Piąta harmoniczna symetrycznej fali prostokątnej nieparzystej h5(t) =b5*sin(5t).
Rozdział 9.7.1 Trajektoria F(njω0t) fali prostokątnej nieparzystej dla n=5 i ω0=1/sek, czyli F(5j1t).
Płaszczyzna Z obraca się z prędkością ω=-5/sek
Rys.9-10
Trajektoria F(5j1t) fali prostokątnej parzystej
Rys.9-10a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-5/sek wokół punktu (0,0) i wykona 5 obrotów w czasie T=2π sek.
Rys.9-10b
Trajektoria F(5j1t)=f(t)*exp(-5j1t) jako wirujący wektor modulowany funkcją f(t).
Wykona 2.5 obrotu w pierwszym półokresie T/2=1π/sek i 0 obrotów drugim półokresie. W okresie T=2π sek promień R=1 dłużej przebywa na dolnej półpłaszczyźnie niż na górnej. Dlatego jego średnią wartością jako wektor będzie sc5=(0,-1/5π)=-1j/5π.
Rys.9-10c
Trajektoria F(5j1t) jako okrąg rysowany przez koniec wektora z Rys.9-10b. Środek ciężkości sc5=(0,-1/5π) wynika z sumowania wektorów na Rys.9-10b i ich średniej w okresie T=2π sek, gdy wykonane jest 5 obrotów płaszczyzny Z. Tak jakby dolny półokrąg był “cięższy” od górnego
Rozdział 9.7.2 Piąta harmoniczna na tle fali prostokątnej nieparzystej czyli c0+h5(t).
Wg Rys. 8-1c z rozdz. 8
c5 jest amplitudą zespoloną piątej harmonicznej
c5=2*sc5=(0,-2/5π) czyli a5=0 i b5=-2/5π
Wg Rys. 8-1e
h5(t)=(2/5π)*sin(5t)≈0.127sin(5t)
Rys. 9-11
co+h5(t)=0.5+(2/5π)*sin(5t) czyli piąta harmoniczna ze składową stałą c0 na tle fali prostokątnej.
Rozdział 9.7.3 Piąte przybliżenie fali prostokątnej nieparzystej czyli S5=c0+h1(t)+h3(t)+h5(t).
Rys.9-12
S5(t)=c0+h1(t)+h3(t)+h5(t)=0.5+(2/π)*sin(1t)+(2/3π)*sin(3t)+(2/5π)*sin(5t)
Piąte przybliżenie jest bardziej podobne do fali prostokątnej niż trzecie z Rys.9-8
Rozdział 9.8 Szósta harmoniczna fali prostokątnej nieparzystej, a właściwie jej brak bo c6=0 –>h6(t)=b6*sin(6t)=0.
Rozdział 9.8.1 Trajektoria F(njω0t) fali prostokątnej nieparzystej dla n=6 i ω0=1/sek, czyli F(6j1t).
Rys.9-13
Trajektoria F(6j1t) fali prostokątnej nieparzystej
Rys.9-13a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-6/sek wokół punktu (0,0) i wykona 6 obrotów w czasie T=2π sek.
Rys.9-13b
Trajektoria F(6j1t)=f(t)*exp(-6j1t) jako wirujący wektor modulowany funkcją f(t). Wykona 3 obroty w pierwszym półokresie T/2=1π/sek i 0 obrotów drugim półokresie. Parametr sc6=0 jako średnia wartość T=2π sek jest oczywisty.
Rys.9-13c
Trajektoria F(6j1t) jako okrąg rysowany przez koniec wektora z Rys.9-13b.
sc6=0
Wniosek
sc6=0 i dlatego harmoniczna dla ω=1/6sek nie istnieje.
Rozdział 9.9 Siódma harmoniczna fali prostokątnej nieparzystej h7(t) =b7*sin(7t).
Rozdział 9.9.1 Trajektoria F(njω0t) fali prostokątnej nieparzystej dla n=7 i ω0=1/sek, czyli F(7j1t).
Płaszczyzna Z obraca się z prędkością ω=-7/sek
Rys.9-14
Trajektoria F(5j1t) fali prostokątnej nieparzystej
Rys.9-14a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-7/sek wokół punktu (0,0) i wykona 7 obrotów w czasie T=2π sek.
Rys.8-14b
Trajektoria F(7j1t)=f(t)*exp(-7j1t) jako wirujący wektor modulowany funkcją f(t).
W czasie T=2π sek promień R=1 dłużej przebywa w dolnej półpłaszczyźnie. Dlatego jego średnią wartością jako wektor będzie (-1/7π, 0)=-j1/7π.
Rys.9-14c
Trajektoria F(7j1t) jako okrąg rysowany przez koniec wektora z Rys.9-17b.
Zwróć uwagę na pojawiający się napis “3.5 obrotu”. To powinno przekonać Cię, że trajektoria F(7j1t) dłużej przebywa na dolnej półpłaszczyźnie Z. Inaczej-ta część trajektorii jest “cięższa”.
Rozdział 9.9.2 Siódma harmoniczna na tle fali prostokątnej parzystej czyli c0+h7(t)
Wg Rys. 8-1c z rozdz. 8
c7 jest amplitudą zespoloną siódmej harmonicznej
c7=2*sc5=(0,-2/7π) czyli a7=0 i b7=-2/7π
Wg Rys. 8-1e
h7(t)=(2/7π)*sin(7t)≈-0.091sin(7t)
Rys. 9-15
co+h7(t)=0.5+(2/7π)*sin(7t) czyli siódma harmoniczna ze składową stałą c0 na tle fali prostokątnej.
Rozdział 9.9.3 Siódme przybliżenie fali prostokątnej parzystej czyli S7=c0+h1(t)+h3(t)+h5(t)+h7(t).
Rys.9-16
S7(t)=c0+h1(t)+h3(t)+h5(t)+h7(t)=0.5+(2/π)*sin(1t)+(2/3π)*sin(3t)+(2/5π)*sin(5t)+(2/7π)*sin(7t)
Siódme przybliżenie jest bardziej podobne do fali prostokątnej niż piąte z Rys.9-12
Rozdział 9.10 Ósma harmoniczna fali prostokątnej parzystej, a właściwie jej brak bo c8=0 –>h8(t)=b8*cos(8t)=0.
Rozdział 9.10.1 Trajektoria F(njω0t) fali prostokątnej parzystej dla n=8 i ω0=1/sek, czyli F(8j1t).
Rys.9-17
Trajektoria F(8j1t) fali prostokątnej parzystej
Rys.9-17a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-8/sek wokół punktu (0,0) i wykona 8 obroty w czasie T=2π sek.
Rys.9-17b
Trajektoria F(8j1t)=f(t)*exp(-8j1t) jako wirujący wektor modulowany funkcją f(t). Wykona 4 obroty w pierwszym półokresie T/2=1π/sek i 0 obrotów drugim półokresie. Parametr sc=0 jako średnia wartość T=2π sek jest oczywisty.
Rys.9-17c
Trajektoria F(8j1t) jako okrąg rysowany przez koniec wektora z Rys.9-17b.
sc8=0
Wniosek
sc8=0 i dlatego harmoniczna dla ω=1/8sek nie istnie.
Rozdział 9.11 Pozostałe harmoniczne fali prostokątnej parzystej czyli dla n=9,10,11…∞
Zauważyliśmy, że środki ciężkości scn trajektorii zbliżają się do scn=(0,0) gdy ω rośnie. W dodatku scn harmonicznych parzystych są zerowe. Oznacza to, że harmoniczne maleją ze wzrostem częstotliwości a dla nieskończenie wielkiej częstotliwości ω amplitudy harmonicznych są zerowe, czyli znikają.
Animacja Rys.9-16 pokazuje, że dla n=7 suma S7(t)=c0+h1(t)+h3(t)+h5(t)+h7(t).
A gdy liczba harmonicznych jest nieskończenie wielka, tzn. n=∞
Wtedy suma tych harmonicznych
S∞(t)=c0+h1(t)+h3(t)+h5(t)+h7(t)+h9(t)+…+h∞(t)
jest falą prostokątną f(t) z Rys. 9-1.
