Wirujące Szeregi Fouriera
Rozdział 6 Jak odfiltrować harmoniczne z funkcji
f(t)=0.5+1.08*cos(1t–33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)
Rozdział 6.1 Wstęp
Im dalej w las tym więcej… W Rozdziale 4 wyłuskaliśmy z funkcji f(t)=0.5*cos(4t) harmoniczną 0.5*cos(4t). Trochę to jak wyciąganie królika z worka, w którym jest tylko jeden królik-harmoniczna 0.5*cos(4t). Banał, ale był to tylko pretekst do poznania metody wirującej płaszczyzny. W Rozdziale 5 jest już ciekawsza funkcja f(t)=1.3+0.7*cos(2t)+0.5*cos(4t). Wyłuskiwanie miało większy sens. W worku są 2, a nawet 3 króliki-dwie harmoniczne i jeszcze składowa stała c0=+1.3. Teraz mamy worek z 4 królikami. Funkcja f(t) ma trzy harmoniczne i składową stałą c0=+0.5. W dodatku harmonicznymi są cosinusy z przesunięciami fazowymi ϕ!
Rozdział 6.2 Jak przy pomocy płaszczyzny wirującej z prędkością ω=n*ω0, wyłuskać harmoniczne z funkcji
f(t)=0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)?
Rozdział 6.2.1 Wstęp
Sprawdzimy wirującą funkcję f(jnω0t) przy różnych prędkościach n*ω0 dla n=0…8 i ω0=1/sek. Naszym celem jest wyłuskanie składowej stałej c0=0.5 oraz trzech harmonicznych. My znamy f(t) jako wzór, czyli znamy c0 i 3 harmoniczne. Załóżmy, że “Ktoś” zna tylko przebieg czasowy z Rys. 6-1b. Czyli co? Pozostaje mu tylko wirująca płaszczyzna.
Funkcja f(t) ma 3 równoważne postacie:
1. f(t)=0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)
2. f(t)=0.5+0.9*cos(1t)+0.6*sin(1t)+0.6*cos(3t)-0.4*sin(3t)+0.4*cos(5t)+0.2*sin(5t)
3. f(t)=Re {0.5+(0.9-j0.6)*exp(+j1t)+(0.6+j0.4)*exp(+j3t)+(0.4-j0.2)*exp(+j5t)}
Ad 1. f(t) z tytułu rozdziału.
Ad 2. f(t) gdzie każdą harmoniczną rozbiliśmy na składową sinus i cosinus.
Ad 3. Jest to część rzeczywista (“Re”) funkcji zespolonej (tego co jest między klamrami { }
Skojarz odpowiednie współczynniki np. (0.9-j0.6)*exp(+j1t) ze współczynnikami cos(1t)+0.6*sin(1t) z Ad. 2.
Wykres f(t) na Rys. 6-1b powstał na podstawie Ad. 1. Na podstawie Ad. 2 i Ad. 3 byłby oczywiście taki sam.
Rozdział 6.2.2 Trajektoria F(0j1t)=f(t)*exp(-0j1t)=f(t)=0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°) czyli bez wirowania
Promień R nie wiruje, ale zmienia się na Rys. 6-1a wzdłuż osi rzeczywistej Re z wg. funkcji okresowej
R(t)=F(0j1t)=f(t)=0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°).
Czyli trajektorią na płaszczyźnie zespolonej Z na Rys. 6-1a będzie pulsująca kreska.
Rys. 6-1
Funkcja f(t)=0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°) w wersji zespolonej i rzeczywistej
Rys. 6-1a
F(0j1t)=f(t)=0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°) w wersji zespolonej.
Rys.6-1b
F(0j1t)=f(t)=0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°) w wersji rzeczywistej, czyli wykres czasowy f(t).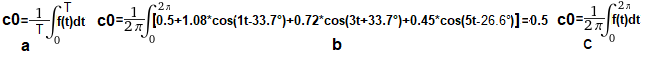
Rys.6-2
Wzór na składową stałą funkcji okresowej f(t), czyli na c0 Szeregu Fouriera
Jest to średnia funkcji f(t) w okresie T
Rys.6-2a
Wzór ogólny dla f(t) o okresie T
Inne spojrzenie na c0=0.5. Jest to także środek ciężkości sc=(0.5) “bujającej” się trajektorii na Rys. 6-1a.
Rys.6-2b
Wzór dla “naszej” f(t) gdy T=2π.
Rys.6-2c
Wzór dla dowolnej f(t) gdy T=2π.
Rozdział 6.2.3 Trajektoria F(1j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-1j1t) czyli z wirowaniem -1ω0=-1/sek
W tym i następnych podrozdziałach pulsujący promień R(t) z Rys.6-1a zacznie wirować z prędkościami –1/sek…–8/sek. Tu animacja będzie trwała T=2π/ω0≈6.28sek i promień R=0.5 z Rys.6-3a wykona 1 obrót. W następnych prędkościach wirowania tj. -2ω0=-2/sek, -3ω0=3/sek…-8ω0=-8/sek, czas każdej animacji też będzie T≈6.28sek. Oznacza to promień R=0.5* wykona 2,3…8 obrotów. Albo inaczej, płaszczyzna zespolona Z wykona 2,3…8 obrotów.
*Uwaga
Jako promień wzorcowy obracającej się płaszczyzny wybrałem R=0.5. Przypadkowo składowa stała też jest c0=0.5
Rys. 6-3
F(1j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-1j1t)
Rys. 6-3a
Promień R=0.5 z -1ω0=-1/sek wykona 1 obrót
Rys.6-3b
W czasie obrotu zmienia się długość promienia zgodnie z funkcją
R(t)=f(t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°).
Realizowana jest więc funkcja zespolona F(1j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-1j1t)
Rys.6-3c
Funkcja zespolona F(1j1t) jako trajektoria.
Trajektoria F(1j1t) krąży wokół środka ciężkości sc1=(0.45,-0.3) z prędkością –1ω0=-1/sek. Jest to wektor i można go też zapisać w postaci wykładniczej sc1=0.54*exp(j-33.7°). W Rozdziale 7 dowiesz się, z sc1=(0.45,-0.3), inaczej sc1=0.54*exp(–j33.7°), można łatwo odczytać pierwszą harmoniczną funkcji jako1.08*cos(1t-33.7°) lub 0.9*cos(1t)+0.6*sin(1t).
Rozdział 6.2.4 Trajektoria f(2j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-2j1t) czyli z wirowaniem -2ω0=-2/sek
Rys.6-4
F(2j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-2j1t) .
Rys. 6-4a
Promień R=0.5 wykona 2 obroty.
Rys.6-4b
Funkcja zespolona F(2j1t) jako wirujący wektor
Rys.6-4c
Funkcja zespolona F(2j1t) jako trajektoria.
Środkiem ciężkości trajektorii F(2j1t) jest sc2=(0,0). Czyli funkcja f(t) nie ma harmonicznej o pulsacji 2ω0=2/sek. To zerowe sc2 nie jest zbyt przekonywujące. Wydaje się, że powinno być trochę przesunięte w prawo. Zauważ jednak, że prędkość trajektorii po lewej stronie jest średnio mniejsza niż po prawej.
Rozdział 6.2.5 TrajektoriaF(3j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°))]*exp(-3j1t) czyli z wirowaniem -3ω0=-3/sek
Rys.6-5
F(3j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-3j1t).
Rys.6-5a
Promień R=0.5 wykona 3 obroty.
Rys.6-5b
Funkcja zespolona F(3j1t) jako wirujący wektor.
Rys.6-5c
Funkcja zespolona F(3j1t)jako trajektoria.
Trajektoria F(3j1t) krąży wokół sc3=(0.3,0.2) z prędkością –3ω0=-3/sek. Jest to wektor i można go też zapisać w postaci wykładniczej sc3=0.36*exp(+j33.7°). W Rozdziale 7 dowiesz się, ze środka ciężkości sc3=(0.3,0.2) lub sc3=0.36*exp(+j33.7°) można łatwo odczytać trzecią harmoniczną funkcji jako 0.72*cos(3t+33.7°) lub 0.6*cos(3t)-0.4*sin(3t).
Rozdział 6.2.6 Trajektoria F(4j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-4j1t) czyli z wirowaniem -4ω0=-4/sek
Rys.6-6
F(4j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-j26.6°)]*exp(-4j1t)
Rys. 6-6a
Promień R=0.5 wykona 4 obroty.
Rys.6-6b
Funkcja zespolona F(4j1t) jako wirujący wektor
Rys.6-6c
Funkcja zespolona F(4j1t) jako trajektoria.
Środkiem ciężkości trajektorii F(4j1t) jest sc4=(0,0).Czyli funkcja f(t) nie ma harmonicznej o pulsacji 4ω0=4/sek.
Podobnie jak na Rys.6-4c środek ciężkości sc4=(0,0) wydaje się zbyt przesunięty w lewo.
Rozdział 6.2.7 Trajektoria F(5j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-j26.6°)]*exp(-5j1t) czyli z wirowaniem -5ω0=-5/sek
Rys.6-7
F(5j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-j26.6°)]*exp(-5j1t).
Rys.6-7a
Promień R=0.5 wykona 5 obrotów.
Rys.6-7b
Funkcja zespolona F(5j1t) jako wirujący wektor.
Rys.6-7c
Funkcja zespolona F(5j1t)jako trajektoria.
Trajektoria F(5j1t) krąży wokół sc5=(0.2,-0.1) z prędkością –5ω0=-5/sek. Jest to wektor i można go też zapisać w postaci wykładniczej sc5=0.36*exp(+j33.7°). W Rozdziale 7 dowiesz się, ze środka ciężkości sc5=(0.2,-0.1) lub sc5=0.36*exp(-j26.6°) można łatwo odczytać piątą harmoniczną funkcji jako 0.45*cos(5t-33.7°) lub 0.4*cos(5t)+0.2*sin(5t).
Rozdział 6.2.8 Trajektoria F(6j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-6j1t) czyli z wirowaniem -6ω0=-6/sek
Rys.6-8
F(4j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-6j1t)
Rys. 6-8a
Promień R=0.5 wykona 6 obrotów.
Rys.6-8b
Funkcja zespolona F(6j1t) jako wirujący wektor
Rys.6-8c
Funkcja zespolona F(6j1t) jako trajektoria.
Środkiem ciężkości trajektorii F(6j1t) jest sc6=(0,0).Czyli funkcja f(t) nie ma harmonicznej o pulsacji 6ω0=6/sek.
Rozdział 6.2.9 Trajektoria F(7j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-7j1t) czyli z wirowaniem -7ω0=-7/sek
Rys.6-9
F(7j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-7j1t)
Rys. 6-9a
Promień R=0.5 wykona 7 obrotów.
Rys.6-9b
Funkcja zespolona F(7j1t) jako wirujący wektor
Rys.6-9c
Funkcja zespolona F(7j1t) jako trajektoria.
Środkiem ciężkości trajektorii F(7j1t) jest sc7=(0,0).Czyli funkcja f(t) nie ma harmonicznej o pulsacji 7ω0=7/sek.
Rozdział 6.2.10 Trajektoria F(8j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-8j1t) czyli z wirowaniem -8ω0=-8/sek
Rys.6-10
F(8j1t)=[0.5+1.08*cos(1t-33.7°)+0.72*cos(3t+33.7°)+0.45*cos(5t-26.6°)]*exp(-8j1t)
Rys. 6-10a
Promień R=0.5 wykona 8 obrotów.
Rys.6-10b
Funkcja zespolona F(8j1t) jako wirujący wektor
Rys.6-10c
Funkcja zespolona F(8j1t) jako trajektoria.
Środkiem ciężkości trajektorii F(7j1t) jest sc8=(0,0).Czyli funkcja f(t) nie ma harmonicznej o pulsacji 8ω0=8/sek.
