Rotating Fourier Series3.

Summation of rotating vectors exp (jωt)

Chapter 3.1 What is this for?
To make it easier to understand the summation of cos (ωt) functions, more broadly – sinusoidal functions.
And this matches Fourier Series, which are the sum of sines and cosines.

Chapter 3.2 General about summing rotating vectors exp (jωt)


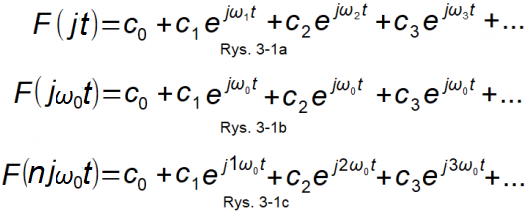
Rys 3-1
Rys 3-1a
Sum of rotating vectors F(jt) where:
c0 is a constant component or otherwise a rotating vector with speed ω=0
c1, c2, c3 … is a complex number which is the initial state of each spinning vector c1*exp (jω1t), c2*exp(jω2t), ec3*exp(jω3t) …
ω1, ω2, ω3 … The pulsations of ω1, ω2, ω3 … are arbitrary! i.e they may or may not be multiples of the first harmonic of n * ω1. This is the most general formula for the sum, and we will not analyze this case.
Rys3-1b
The sum of rotating F(jω0t) vectors with the same pulsation ω0.
It is a vector-complex number c = c1 + c2 + c3 + … rotating at speed ω0.
The real number c0 is a constant component.
The sum of the sinusoids and cosine waves is also a sinusoid with the same pulsation ω0 and the corresponding phase shift φ.
It is used in classical electrical engineering, where power plants generate electricity with a constant frequency f=50H.
The subject has already been thoroughly worked out, probably in the nineteenth century.
Example with animation in chapter 3.3.
Figure 3-1c
This is what we will mainly deal with.
Ie. the sum of rotating vectors with increasing pulsations 1ω0,2ω0, 3ω0 …
I emphasize that each pulsation is a multiple of the fundamental pulsation 1ω0, not any ω1, ω2, ω3 … as in Rys.3-1a
Examples with animation in chapters 3.4 … 7

Chapter 3.3 The sum of 2 rotating vectors exp (jωt) with the same pulsation ω0 = 1 / sec
Chapter 3.3.1   1*exp(j1t) -j1exp(j1t)
The case of Fig.3-1b when c0 =0, c1=1, c2=1*exp(-jπ/2)=-j1 and c3=c1+c2=1-j1=√2*exp(-jπ/4)
The numbers c1, c2 and c3 are the initial states of the spinning vectors as in Rys.3-2 before the animation.
Note that the vector c2 lags π/2=90 ° with respect to c1.

Fig. 3-2
The sum of 2 rotating vectors as:
1exp (j1t)-j1*exp(j1t) or (1-1j)exp(j1t) or √2exp(-jπ/4)*exp(j1t) where  -π/4=-45º.
The right vector is the sum of the 2 left vectors at any moment and has the parameters A=√2, ω=1/sec and ϕ=-π/4=-45º.
At the initial moment, that is before pressing “Start”, the sum of the right vector is correct (add left vectors -> “diagonal of the square”). Then stop the simulation at any time by clicking on the drawing or “Start” and check approximately if it is correct using .
The most important conclusion.
When all vectors have the same speed ω0, their sum is also a rotating vector with the same speed ω0, length A and phase ϕ.
Note 1
Applies to any number of rotating vectors.
Note 2
The relative position of all 3 rotatingg vectors to each other is constant! This makes it much easier to analyze electrical circuits. When this is not the case as in Rys.3-1a or 3-1c, and the vectors rotate at different speeds, the sum vector changes length and velocity! You will find out about this in Chapter 3.4.

Chapter 3.4 Sum F(jω0t)=1exp(j1t)+1exp (j2t)
Chapter 3.4.1 Vector-only version
We begin to study the sums of rotating vectors with different pulsations.
Vector only means that the ends of the vectors do not draw the trajectory.
The case of Rys. 3-1c when c0=0 c1=1, c2=1 and ω0=1/sec

Fig. 3-3
F(jω0t)= 1*exp (1jt)+1*exp (2jt) (ω0 = 1 / sec)
You see complex functions as rotating vectors
1*exp(1jt), 1*exp(2jt) and their sum 1*exp(1jt)+1*exp (2jt)
You can clearly see the speed of 1*exp(2jt) twice as high. Try to stop the animation at different times t and check if the right function is a vector sum of 2 left ones. Here I am asking for some tolerance for the author’s ineffective use of the animation program.

Rozdział 3.4.2 Trajektoria czyli wersja “tylko śladowa”

Chapter 3.4.2 Trajectory or ” trace only” version
“Trace only” means that the ends of the vectors from Fig.3-2 draw a trace. The vectors themselves are invisible and this trace is the trajectory F(jω0t). This is the case of Fig. 3-1c when c0=0 c1=1, c2=1 and ω0=1/sec. Only one period of animation is shown. Further rotations follow the same tracks and the animation looks static! Also in the next animations.
Here and further we will limit ourselves to the “only with a trace” version. The “vector” version of this case is the animation in Fig. 3-3.

Fig. 3-4
F(jω0t)=1*exp(1jt)+1*exp(2jt)
The right animation is the sum of the left 2. Note that 1*exp(2jt) “stopped” after the first half period.
But the trajectory is still rotating, just on the same track!

Chapter 3.5  F(jω0t)= 1exp(j1t)+0.7exp(j2t)

Fig. 3-5
F(jω0t)=1exp(j1t)+0.7exp(j2t)

Chapter 3.6 F(jω0t)=1exp(j1t)+1exp(j2t-π/6)

Fys. 3-6
F(jω0t)=1exp(j1t)+1exp(j2t-π/6)
φ=-π/6 is the actual delay φ=-30º.
The previous examples had a phase shift of φ = 0º, now one of the components 1exp(j2t-π /6) has φ non-zero. The lag component 1exp (j2t-π/6) causes a counterclockwise rotation.
Compare with Rys. 3-4, where the second component of j2t has a delay of φ=0. Try to explain it to yourself somehow.

Chapter 3.7 F(jω0t)=0.3exp(j1t)+0.5exp(j2t-π/6)+0.45exp(j2t+π/4)
More fancy trajectory then.

Fig. 3-7
F(jω0t)=0.3exp(j1t)+0.5exp(j2t-π/6)+0.45exp(j2t+π/4)
Let me remind you that the sum vector is spinning all the time, even after the animation ends after the first T period.
The red point at (0,0) is also the so-called the center of gravity of the trajectory. More on this in the next chapter.

Rozdział 3.8 Conclusions

Fig. 3-8
F(jω0t) the sum of rotating vectors in which:
– c0 is a constant component or a formally rotating vector with pulsation ω=0.
It is a real number (and a complex number at the same time!)
– c1exp (1jω0) is a vector rotating at speed 1ω0
– c2exp (2jω0) is a vector rotating at speed 2ω0
– c3exp (3jω0) is a vector rotating at speed 3ω0
…
And the complex numbers c1, c2, c3 … are the initial states of these rotating vectors.
Some people treat the initial state as the beginning of the world, and others as the moment t=0 when we start the experiment.
Take a moment to look at Fig.4-8 in the next chapter.
There are coefficients c0=-0.5, c1=0.9-j0.6, c2=0.6 j0.4, and c3=0.4-j0.2 for a particular Fourier Series.
The trajectory F(jω0t) is drawn after the period T along the same path. This period corresponds to the first harmonic 1ω0 and T≈6.28sec.
The formula Fig.3-7 describes the trajectory for ω0=1/sec. The shape of the trajectory will be exactly the same for ω0=2/sec, ω0=3/sec… Only that it will rotate 2, 3… times faster.