Wirujące Szeregi Fouriera
Rozdział 10
Szereg Fouriera fali prostokątnej z przesunięciem -30°.
Rozdział 10.1 Wstęp
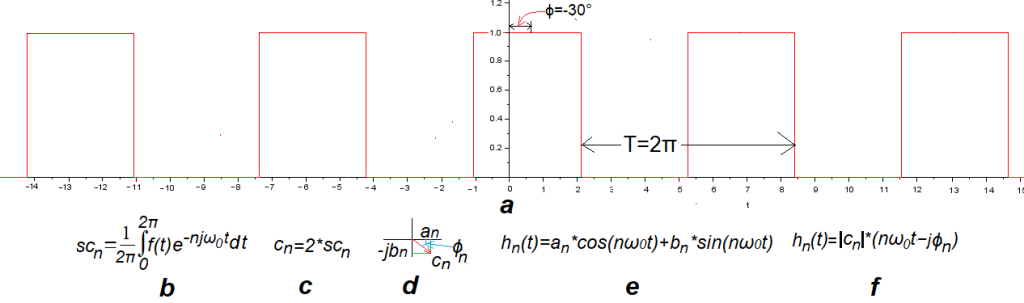
Rys.10-1
Fala prostokątna f(t) A=1, ω=1/sek i ϕ=-30° albo -π/6.
Parametr ϕ=-30° fali oznacza, że jest przesunięta o –30° względem fali parzystej z rozdziału 8. Nie jest to więc funkcja parzysta ani nieparzysta. Taka nijaka. Fala parzysta miała tylko harmoniczne cosinusoidalne czyli an≠0 i bn=0. Z kolei nieparzysta tylko sinusoidalne tzn. składowe an=0 i bn≠0. Spodziewamy się, że teraz wystąpią składowe cosinusoidalne i sinusoidalne an≠0 i bn≠0.
Rozdział 10.2 Składowa stała czyli c0=0.5.
Składową stałą, jako wartość średnia w okresie T=2π sek jest c0=0.5. Nie zależy ona od fazy przesunięcia ϕ.
Rozdział 10.2.1 Trajektoria F(nj1t) dla n=0 i ω0=1/sek, czyli F(0j1t).
Rys.10-2
Trajektoria F(0j1) funkcji f(t) fali prostokątnej z przesunięciem -30°, czyli o parametrach:
A=1-amplltuda
ω0=1/sek-pulsacja odpowiadająca okresowi T=2πsek≈6.28sek.
ϕ=-30°=-π/6
50%-wypełnienie
Rys.10-2a
Trajektoria F(0j1t) odpowiadająca trajektorii F(njω0t) dla n=0 i ω0=1/sek.
Nieruchoma płaszczyzna Z, gdzie na osi rzeczywistej Re Z wektor zmienia się wg. funkcji f(t) z Rys.10-2b.
Rys.10-2b
Wykres czasowy f(t) fali prostokątnej z ϕ=-30°=-π/6
W następnych podrozdziałach płaszczyzna Z zacznie obracać się z prędkościami ω= -nω0, czyli z prędkościami -1/sek,-2/sek…-8/sek. Koniec wektora będzie rysował trajektorie F(njω0). Z nich odczytamy harmoniczne dla pulsacji nω0.
Rozdział 10.3 Pierwsza harmoniczna czyli h1(t).
Rozdział 10.3.1 Trajektoria F(nj1t) dla n=1 i ω0=1/sek, czyli F(1j1t).
Rys.10-3
Trajektoria F(1j1t) fali prostokątnej z przesunięciem -30°
Porównaj rysunek z analogicznym Rys.8-3 z rozdz. 8 dla fali prostokątnej parzystej. Tam wektor sc1 miał przesunięcie ϕ=0° i był przedstawiony jako liczba zespolona w postaci algebraicznej sc1=(1/π,0) lub inaczej
1/π+j0. Równie dobrze mogła być to postać wykładnicza sc1=1/π*exp(j0°), gdzie wyraźnie widać amplitudę
A=1/π i fazę ϕ=0°. W tym rozdziale używać będziemy wersji wykładniczej i dlatego środek ciężkości trajektorii z Rys. 10-3c to sc1=|1/π|*exp(-j30°). Tu |1/π| to tzw. moduł sc1
Z wersji wykładniczej można łatwo przejść na algebraiczną i vice versa:
sc1=1/π*exp(-j30°)=1/π*[cos(-30°)+jsin(-30°)]≈0.275-j0.159
Wektor sc1 jest średnią wartością obracającego się wektora z Rys.10-3b w okresie T=2π sek
liczoną ze wzoru Rys. 7-2b rozdz.7.
Revenons à nos moutons, czyli wróćmy do tematu.
Rys.10-3a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-1/sek wokół punktu (0,0) w czasie T=2π sek i wykona 1 obrót.
Rys.10-3b
Trajektoria F(1j1t)=f(t)*exp(-1j1t) jako wirujący wektor modulowany funkcją f(t). Funkcja f(t) jest falą prostokątną z Rys.10-2b.
Płaszczyzna Z z Rys.10-2a zacznie się obracać z prędkością ω=-1/sek. Powstanie wirujący wektor F(1j1t)=f(t)*exp(-1j1t). Płaszczyzna Z wykona 1 obrót, ale trajektoria jako wirujący wektor F(1j1t)=f(t)*exp(-1j1t) tylko 1 “półobrót”.
Rys.10-3c
Trajektoria F(1j1t) jako półokrąg rysowany przez koniec wektora z Rys.10-3b.
W czasie 1 obrotu płaszczyzny Z o kąt 0…2π wszystkie wektory są sumowane wektorowo i obliczana jest ich średnia w okresie T=2π sek ze wzoru Rys. 7-2b rozdz. 7. Jest to wektor sc1=(1/π)*exp(-j30°). Trajektoria jest obrócona względem tej z Rys. 8-3c rozdz. 8 o kąt ϕ=-30°.
Uwaga do Rys 10-3b,c
Powyższe animacje sugerują, że górne i dolne części trajektorii są rozdzielone przerwą T=π sek. Ale tak jest tylko na początku w czasie t=0…2π sek! Później nie ma tej przerwy i ruch po trajektorii jest ciągły.
Rozdział 10.3.2 Pierwsza harmoniczna na tle fali prostokątnej czyli c0+h1(t) albo inaczej pierwsze przybliżenie fali prostokątnej.
Składowa stała c0 to średnia w okresie T=2π czyli c0=a0=0.5.
Wg Rys. 10-3c
sc1=|sc1|*exp(jϕ)=(1/π)*exp(-j30°)
c1=2*sc1=(2/π)*exp(-j30°) czyli |c1|=2/π ϕ=-30°
Wg Rys. 8-1f rozdział 8
h1(t)=(2/π)*cos(1t-30°)≈0.637*cos(1t-30°)
Rys.10-4
S1(t)=c0+h1(t) czyli pierwsza harmoniczna ze składową stałą c0=0.5 na tle fali prostokątnej.
Jest to pierwsze przybliżenie naszej fali prostokątnej.
Rozdział 10.4 Druga harmoniczna fali , a właściwie jej brak bo c2=0–>h2(t)=0.
Rozdział 10.4.1 Trajektoria F(njω0t) dla n=2 i ω0=1/sek, czyli F(2j1t).
Płaszczyzna Z obraca się z prędkością ω=-2/sek
Rys.10-5
Trajektoria F(2j1t) fali prostokątnej z przesunięciem -30°
Rys.10-5a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-2/sek wokół punktu (0,0) i wykona 2 obroty w czasie T=2π sek.
Rys.10-5b
Trajektoria F(2j1t)=f(t)*exp(-2j1t) jako wirujący wektor modulowany funkcją f(t).
W czasie 2π sek płaszczyzna Z wykona 2 obroty, ale promień R=1 zrobi tylko 1 obrót składający się z pierwszego obrotu 240° i z drugiego obrotu 120° przerwą 1π sek między nimi.
Rys.10-5c
Trajektoria F(2j1t) jako okrąg rysowany przez koniec wektora z Rys.10-5b.
Ewidentnie sc2=0. Zauważ, że z samego tylko okręgu wartość sc2=0 nie jest oczywista! Przecież okrąg mógł być narysowany np. 1.5 razy. Na szczęście ten 1 pełny obrót, choć z przerwą w środku, jest widoczny na 10-5b.
Wniosek
sc2=0 i dlatego harmoniczna dla ω=2/sek nie istnieje.
Rozdział 10.5 Trzecia harmoniczna fali czyli h3(t).
Rozdział 10.5.1 Trajektoria F(njω0t) dla n=3 i ω0=1/sek, czyli F(3j1t).
Płaszczyzna Z obraca się z prędkością ω=-3/sek
Rys.10-6
Trajektoria F(3j1t) fali prostokątnej z przesunięciem -30°
Rys.10-6a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-3/sek wokół punktu (0,0) i wykona 3 obroty w czasie T=2π sek.
Rys.10-6b
Trajektoria F(3j1t)=f(t)*exp(-3j1t) jako wirujący wektor modulowany funkcją f(t).
W czasie 2π sek płaszczyzna Z wykona 3 obroty, ale promień R=1 zrobi tylko 1.5 obrotu składający się z pierwszego obrotu 360° i z drugiego obrotu 180° z przerwą 1π sek między nimi. Promień R. Promień R=1 dłużej przebywa w górnej półpłaszczyźnie niż w dolnej. Dlatego średnią wartością wektora jest sc3=(0,1/3π)=1j/3π
Rys.10-6c
Trajektoria F(3j1t) jako okrąg rysowany przez koniec wektora z Rys.10-6b.
Środek ciężkości sc3=( 0,1/3π)=1j/3π.
Rozdział 10.5.2 Trzecia harmoniczna na tle fali prostokątnej z czyli c0+h3(t).
Wg Rys. 10-3c
sc3=|sc3|*exp(jϕ)=(1/3π)*exp(j90°)
c1=2*sc1=(2/3π)*exp(j90°) czyli |c1|=2/3π ϕ=90°
Wg Rys. 8-1f rozdział 8
h3(t)=(2/3π)*cos(3t+90°)≈-0.212*sin(3t)
Rys.10-7
S3(t)=c0+h3(t) czyli trzecia harmoniczna ze składową stałą c0=a0=0.5 na tle fali prostokątnej.
Rozdział 10.5.3 Trzecie przybliżenie fali prostokątnej czyli S3=c0+h1(t)+h3(t).
Rys.10-8
S3(t)=c0+h1(t)+h3(t)
Trzecie przybliżenie jest bardziej podobne do fali prostokątnej niż pierwsze z Rys.10-4
Rozdział 10.6 Czwarta harmoniczna a właściwie jej brak, bo c4=0–>h4(t)=0.
Rozdział 10.6.1 Trajektoria F(njω0t) dla n=4 i ω0=1/sek, czyli F(4j1t).
Płaszczyzna Z obraca się z prędkością ω=-4/sek
Rys.10-9
Trajektoria F(4j1t) fali prostokątnej z przesunięciem -30°
Rys.10-9a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-4/sek wokół punktu (0,0) i wykona 4 obroty w czasie T=2π sek.
Rys.10-9b
Trajektoria F(4j1t)=f(t)*exp(-4j1t) jako wirujący wektor modulowany funkcją f(t).
W czasie 2π sek płaszczyzna Z wykona 4 obroty, ale promień R=1 zrobi pełne 2 obroty składający się z pierwszego 480° i z drugiego 240° przerwą 1π sek między nimi.
Rys.10-9c
Trajektoria F(2j1t) jako okrąg rysowany przez koniec wektora z Rys.10-9b.
Ewidentnie sc4=0.
Wniosek
sc4=0 i dlatego harmoniczna dla ω=2/sek nie istnieje.
Rozdział 10.7 Piąta harmoniczna czyli h5(t).
Rozdział 10.7.1 Trajektoria F(njω0t) dla n=5 i ω0=1/sek, czyli F(5j1t).
Płaszczyzna Z obraca się z prędkością ω=-5/sek
Rys. 10-10
Trajektoria F(5j1t) fali prostokątnej z przesunięciem -30°
Rys.10-10a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-5/sek wokół punktu (0,0) i wykona 5 obrotów w czasie T=2π sek.
Rys.10-10b
Trajektoria F(5j1t)=f(t)*exp(-5j1t) jako wirujący wektor modulowany funkcją f(t).
W czasie 2π sek płaszczyzna Z wykona 5 obrotów, ale promień R=1 zrobi tylko 2.5 obrotów (900°) w tym pierwszy 585° i drugi 315° przerwą 1π sek między nimi. Promień R=1 dłużej przebywa w lewej dolnej ćwiartce niż w pozostałych. Dlatego średnią wartością wektora jest sc5=(1/5π)*exp(-j150°)
Rys.10-10c
Trajektoria F(5j1t) jako okrąg rysowany przez koniec wektora z Rys.10-10b.
Środek ciężkości sc5=(1/5π)*exp(-j150°).
Rozdział 10.7.2 Piąta harmoniczna na tle fali prostokątnej czyli c0+h5(t).
Wg Rys. 10-5c
sc5=|sc5|*exp(jϕ)=(1/5π)*exp(-j150°).
c5=2*sc5=(2/5π)*exp(-j150°) czyli |c1|=2/5π ϕ=-150°
Wg Rys. 8-1f rozdział 8
h5(t)=(2/5π)*cos(5t-150°)≈-0.127*cos(5t+30°)
Rys. 10-11
S5(t)=c0+h5(t) czyli piąta harmoniczna ze składową stałą c0=a0=0.5 na tle fali prostokątnej.
Rozdział 10.7.3 Piąte przybliżenie czyli S5(t)=c0+h1(t)+h3(t)+h5(t).
Rys.10-12
S5(t)=c0+h1(t)+h3(t)+h5(t)
Piąte przybliżenie jest bardziej podobne do fali prostokątnej niż trzecie z Rys.10-8
Rozdział 10.8 Szósta harmoniczna fali, a właściwie jej brak bo c6=0 –>h6(t)=0.
Rozdział 10.8.1 Trajektoria F(njω0t) dla n=6 i ω0=1/sek, czyli F(6j1t).
Rys.10-13
Trajektoria F(6j1t) fali prostokątnej z przesunięciem -30°
Rys.10-13a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-6/sek wokół punktu (0,0) i wykona 6 obrotów w czasie T=2π sek.
Rys.10-13b
Trajektoria F(6j1t)=f(t)*exp(-6j1t) jako wirujący wektor modulowany funkcją f(t).
W czasie 2π sek płaszczyzna Z wykona 6 obrotów, ale promień R=1 zrobi pełne 3 obroty składający się z pierwszego 720° i z drugiego 360° przerwą 1π sek między nimi.
Rys.10-13c
Trajektoria F(6j1t) jako okrąg rysowany przez koniec wektora z Rys.10-13b.
Ewidentnie sc6=0.
Wniosek
sc6=0 i dlatego harmoniczna dla ω=6/sek nie istnieje.
Rozdział 10.9 Siódma harmoniczna czyli h7(t).
Rozdział 10.9.1 Trajektoria F(njω0t) dla n=7 i ω0=1/sek, czyli F(7j1t).
Płaszczyzna Z obraca się z prędkością ω=-7/sek
Wektor sc7 jest tak mały, że ledwo go widać. Musisz go sobie wyobrazić.
Rys. 10-14
Trajektoria F(7j1t) fali prostokątnej z przesunięciem -30°
Rys.10-14a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-7/sek wokół punktu (0,0) i wykona 7 obrotów w czasie T=2π sek.
Rys.10-14b
Trajektoria F(7j1t)=f(t)*exp(-7j1t) jako wirujący wektor modulowany funkcją f(t).
W czasie 2π sek płaszczyzna Z wykona 7 obrotów (2520°), ale promień R=1 zrobi tylko 3.5 obrotów (1260°) w tym w pierwszym cyklu 2 i 1/3 obrotu (840°) i w drugim cyklu 1 i 1/6 obrotu (420°) z przerwą 1π sek między nimi. Promień R=1 trochę dłużej przebywa w prawej dolnej ćwiartce niż w pozostałych. Dlatego średnią wartością wektora jest sc7=(1/7π)*exp(-j30°)
Rys.10-10c
Trajektoria F(7j1t) jako okrąg rysowany przez koniec wektora z Rys.14b.
Środek ciężkości sc7=(1/7π)*exp(-j30°).
Rozdział 10.9.2 Siódma harmoniczna na tle fali prostokątnej czyli c0+h7(t).
Wg Rys. 10-14c
sc7=|sc7|*exp(jϕ)=(1/7π)*exp(-j30°).
c7=2*sc7=(2/7π)*exp(-j30°) czyli |c7|=2/7π ϕ=-30°°
Wg Rys. 8-1f rozdział 8
h7(t)=(2/7π)*cos(7t-30°)≈-0.127*cos(7t-30°)
Rys.10-15
S7(t)=c0+h7(t) czyli siódma harmoniczna ze składową stałą c0=a0=0.5 na tle fali prostokątnej.
Rozdział 10.9.3 Siódme przybliżenie czyli S7(t)=c0+h1(t)+h3(t)+h5(t)+h7(t).
Rys. 10-16
S7(t)=c0+h1(t)+h3(t)+h5(t)+h7(t)
Siódme przybliżenie jest bardziej podobne do fali prostokątnej niż piąte z Rys.10-12
Rozdział 10.10 Ósma harmoniczna a właściwie jej brak bo c8=0 –>h8(t)=0.
Rozdział 10.10.1 Trajektoria F(njω0t) dla n=8 i ω0=1/sek, czyli F(8j1t).
Rys.10-17
Trajektoria F(8j1t) fali prostokątnej z przesunięciem -30°
Rys.10-17a
Promień R=1 jako wektor (1,0) obraca się z prędkością ω=-8/sek wokół punktu (0,0) i wykona 8 obrotów w czasie T=2π sek.
Rys.10-17b
Trajektoria F(8j1t)=f(t)*exp(-8j1t) jako wirujący wektor modulowany funkcją f(t).
W czasie 2π sek płaszczyzna Z wykona 8 obrotów, ale promień R=1 zrobi pełne 4 obroty tylko w pierwszym etapie.
Rys.10-17c
Trajektoria F(8j1t) jako okrąg rysowany przez koniec wektora z Rys.10-17b.
Ewidentnie sc8=0.
Wniosek
sc8=0 i dlatego harmoniczna dla ω=8/sek nie istnieje.
