Transformata Fouriera
Rozdz. 7. Transformata Fouriera rachunkowo
Rozdz. 7.1 Wstęp
Moim głównym celem było zrozumienie samej idei Transformaty Fouriera oraz to, że jest ona jakby ciągłą wersją Szeregów Fouriera.
Szereg Fouriera dotyczy kolejnych harmonicznych funkcji okresowych f(t) o pulsacji ω0=2π/To, które w wersji zespolonej są zespolonymi współczynnikami c(n):
– c(0) jest składową stałą
– c(1), c(2)…c(n) są amplitudami zespolonymi harmonicznych o pulsacjach 1ω0, 2ω0… nω0…
Amplitudy i fazy są bezpośrednio widoczne w c(1), c(2)…c(n).
Transformata Fouriera dotyczy harmonicznych nieokresowych funkcji f(t). Traktujemy ją jako funkcję okresową, ale o tylko jednym okresie To=∞. Prowadzi to do pewnych dziwnych rzeczy. Składowa stała i wszystkie harmoniczne są nieskończenie małe. Przyjmujemy je jako zerowe, chociaż istnieją! Przejście jednej harmonicznej w drugą jest ciągłe, dlatego zamiast konkretnej c(ω) mamy ich średnią w zakresie ω-dω…ω…ω+dω. Ta średnia to inaczej gęstość amplitud zespolonych c(ω)/dω. Ściślej, to transformatą jest 2π*c(ω)/dω. W tym rozdziale pokażemy jak obliczać Transformaty Fouriera funkcji nieokresowych z definicji. Czyli tak jak to się zwykle robi*, a nie poprzez Szereg Fouriera gdy To=∞. Wcześniej zrobiliśmy to w rozdz.4 i 6 korzystając z Szeregów Fouriera przy założeniu, że okres To=∞. Wyniki powinny być identyczne.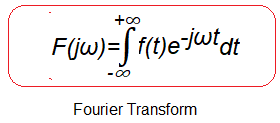
Rys.7-1
Wzór na Transformatę Fouriera
*Obliczanie transformat ułatwiają różne wzory pochodzące od powyższej definicji. Jakieś sploty funkcji, residua itd. Także transformaty całek, pochodnych, funkcji przesuniętych w czasie. Sprawy rachunkowe nie są jednak głównym celem tego artykułu.
Rozdz. 7.2 Transformata Fouriera pojedynczego impulsu prostokątnego
Rys.7-2
Funkcja f(t) jako pojedynczy impuls prostokątny A=1sek w czasie t=-0.5sek…+0.5sek
Obliczymy transformatę F(jω) funkcji f(t) korzystając ze wzoru Rys.7-1.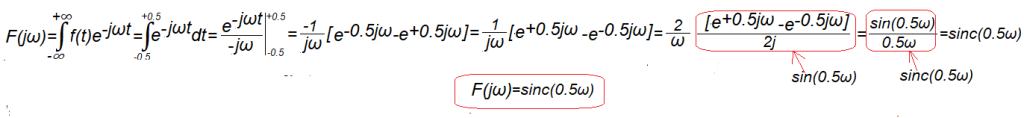
Rys.7-3
Obliczenie transformaty F(jω) funkcji f(t) z Rys.7-2
Przedział całkowania w zakresie t=-0.5…+0.5. W pozostałym zakresie tj. t=-∞..-0.5 i t=+0.5…+∞ funkcja podcałkowa jest zerowa i nie ma wpływu na wartość całki. Niech Cię nie zdziwi, że w pewnym momencie dość skomplikowany iloraz liczb zespolonych zmieni się w poczciwą funkcję rzeczywistą sin(0.5ω). No cóż, taka jest matematyka, a jak nie wierzysz to sprawdź programem WolframAlfA. 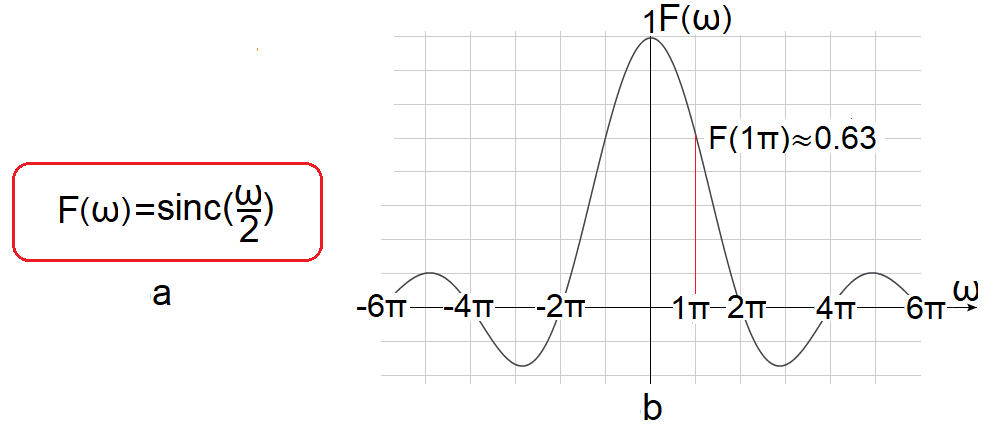
Rys.7-4
Transformata F(jω) funkcji f(t) z Rys.6-1
Jak traktować np. F(1π)≈0.63? Już dobrze wiesz, że chociaż amplituda dla ω=1π/sek istnieje, to jest nieskończenie mała, z pewnym ociąganiem się można powiedzieć, że jest zerowa. Natomiast zmienia się ona w sposób ciągły i w przedziale np. 1π/sek-dω…+1π/sek…1π/sek+dω jej średnią wartością względem ω jest właśnie F(1π)≈0.63.
Wynik jest oczywiście taki sam jak na Rys.4-3 w rozdz.4. Tam traktowaliśmy f(t) jako okresową o To=∞ i dlatego mogliśmy skorzystać ze wzorów na Szereg Fouriera. Uwaga dotyczy także rozdz.7.3. Przypominam, że f(t) jest funkcją parzystą, i dlatego jej transformata F(jω) jest funkcją rzeczywistą, którą można przedstawić w postaci zwykłego wykresu.
Jeszcze jedno. Wyrażenie F(jω) i F(ω) można używać wymiennie. Tak czy owak, wynikiem jest funkcja zespolona, która może być także rzeczywistą, tak jak na Rys.7-4.
Rozdz. 7.3 Transformata Fouriera funkcji t=exp(-t) w przedziale t=0…+∞
Czyli takiej jak w rozdz.6
Rys.7-5
Funkcja f(t) jako jako wykładnicza exp(-t) w przedziale t=0…+∞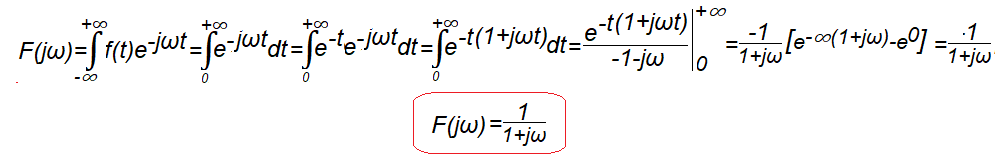
Rys.7-6
Obliczenie transformaty F(jω) funkcji f(t) z Rys.7-5
Nie jest to funkcja parzysta i dlatego jej transformata jest funkcją w pełni zespoloną.
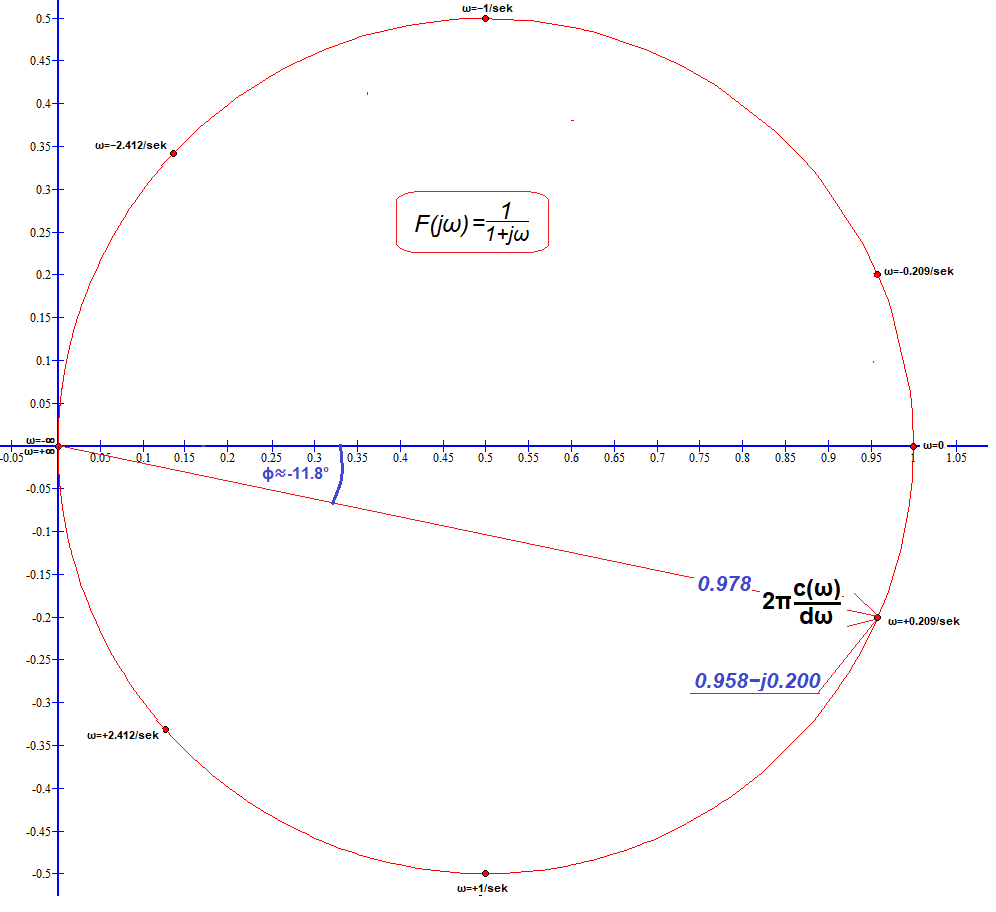
Rys.7-7
Wykres transformaty F(jω)=1/(1+jω)
Dla ω=0.209/sek obliczyliśmy F(j+0.209)=1/(1+j0.209)≈0.209-j0.200=0.978*exp(-j11.8º) jako czerwony wektor. A jak? Np. wstawiając 1/(1+0.209i) do okienka w https://www.wolframalpha.com. F(jω) obliczyliśmy też ze wzoru dla ω=-2.412/sek-1/sek,+1/sek i +2.412/sek te liczby zespolone oznaczyliśmy czerwonymi kropkami. A ω=+∞,-∞? Tu założyliśmy ω=+1000,-1000 jako “prawie” nieskończoności. Tak jak się spodziewaliśmy F(jω)≈0. Nie muszę dodawać, że wszystkie wartości F(jω) dla ω=-∞…+∞ tworzą okrąg.
