Transformata Fouriera
Rozdz. 6. Transformata Fouriera funkcji wykładniczej
Rozdz. 6.1 Opis funkcji
W rozdz. 3 i 4 Poznałeś już transformatę pojedynczego impulsu prostokątnego, który był przykładem funkcji parzystej. Czas na bardziej ogólną, która nie musi być parzystą.
Jest nią np. funkcja f(t).
f(t)=0 dla t<0
f(t)=exp(-1t) dla t>=0
Rys. 6-1
Funkcja f(t).
W pierwszej f(t) wygląda jak pojedynczy impuls o skończonym czasie trwania. Ale on trwa cały czas od t=0 do t=+∞! Potraktujemy f(t) jako okresową o To=∞. Ale najpierw jako “naprawdę” okresową, czyli o skończonym okresie To. Transformatę obliczymy z Szeregów Fouriera. Takie podejście, a nie z gotowego wzoru całkowego pozwoli lepiej zrozumieć samą ideę transformaty.
Rozdz. 6.2 Szereg Fouriera funkcji f(t) o okresie To=15sek
Rozdz. 6.2.1 Wykres funkcji

Rys. 6-2
Funkcja okresowa f(t) okresie To=15sek
Czyli pierwsze przybliżenie funkcji f(t) z Rys. 6-1.
Dlaczego przybliżenie? Bo w przedziale np. t=-7.5…0…+7.5 sek widziałbyś tylko nieokresową funkcję f(t) z Rys. 6-1!
Rozdz. 6.2.2 Przypomnienie wzoru na Zespolony Szereg Fouriera
Zastosujemy ogólny wzór Szeregu Fouriera na c(n) w wersji zespolonej dla pulsacji dodatnich i ujemnych.
Składowa stała c(0), czyli dla n=0, też pod niego podpada.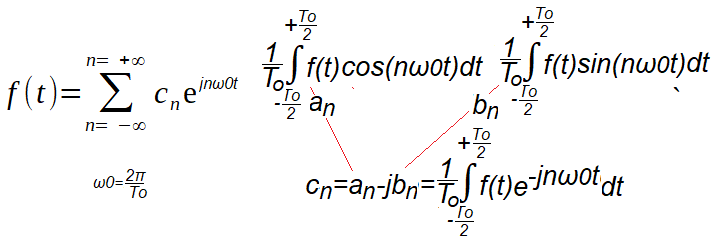
Rys.6-3
Zespolony wzór na Szereg Fouriera
Trygonometryczny wzór na Szereg Fouriera to 2 osobne wzory na a(n) i b(n). Pamiętaj, że pulsacja ω0 pierwszej harmonicznej jest także odstępem Δω między kolejnymi harmonicznymi!
Rozdz. 6.2.3 Obliczenie zespolonych współczynników Fouriera c(n) programem Wolfram Alfa.
Pulsacja pierwszej harmonicznej–>ω0=2π/To=2π/15sek≈0.419/sek
Przedział całkowania–>-To/2…+To/2=-7.5sek…+7.5sek.
Obliczmy np. c(n) dla n=+3.
Instrukcja WolframAlfa:
(1/15)*integrate exp(-t)*heaviside(t)*exp(-2pi*i*3*t/15)dx from t=-7.5 to 7.5
1.Aby ją zrealizować, skopiuj powyższy tekst, czyli cntrl c…
2.Kliknij https://www.wolframalpha.com
3.Wklej tekst do okienka.
4. Rób co każe obrazek.
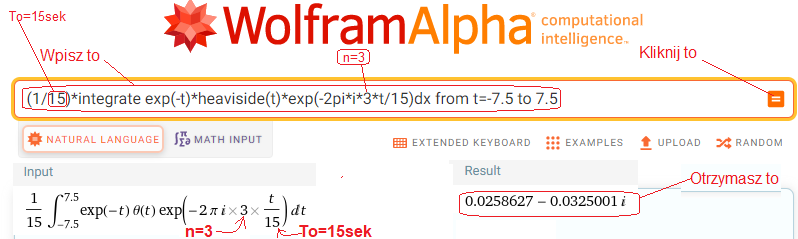
Rys.6-4
Instrukcja WolframAlfa obliczająca wzór na c(n) z Rys.6-3 dla n=+3, To=15 sek i f(t) z Rys.6-2
WolframAlfa pokazał także wiele innych rzeczy, ale nas interesuje tylko wynik, tj. liczba zespolona
c(+3)=c(+3ω0)=0.0259627-j0.0325001 dla ω0=2π/15sek≈0.419*1/sek—>Rys.6-5.
Jest to amplituda zespolona trzeciej harmonicznej, czyli dla ω=3ω0.
Rozdz. 6.2.4 Współczynniki c(n) na płaszczyźnie zespolonej Re z/Im z
Po obliczeniach dla n=-12…0…+12 wyniki c(n) wstawiłem na płaszczyznę zespoloną Re z/Im z. Zespolone współczynniki Fouriera c(n) pojawią się na okręgu A. Wśród nich jest obliczony przed chwilą współczynnik/punkt c(+3)=c(-3ω0)=0.0259627-j0.0325001. Obliczyliśmy także c(+1000)≈c(ω=-∞) i c(-1000)≈c(ω=+∞) jako prawie z=(0,0). Innymi słowy n=1000 robi w obliczeniach za nieskończoność.
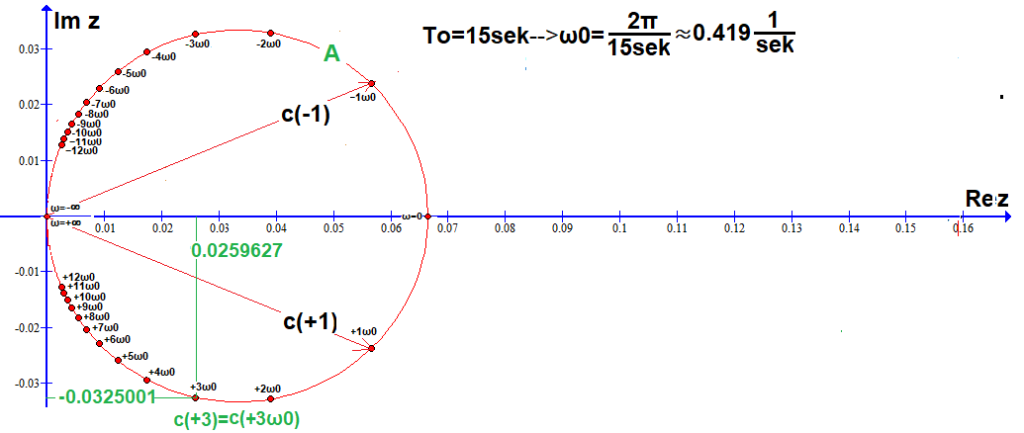
Rys. 6-5
26 współczynników c(n) Szeregu Fouriera na okręgu A obliczone programem WolframAlfa.
W tym: 12 dolnych c(n), 12 górnych, c(ω=0), c(ω=+∞)=c(ω=-∞)=(0,0).
Tworzą dolny półokrąg dla n>0, i górny dla n<0. Każdy punkt c(n) dla n=-12…+12 jest amplitudą zespoloną dla n-tej harmonicznej. Czyli niezbyt ściśle-n-tą harmoniczną. Pokazałem je jako wektory tylko dla c(+1)=c(+1ω0) i c(-1)=c(-1ω0). Pozostałe c(n) ze względu na czytelność są tylko kropkami. Wykres jest odpowiednikiem wykresów prążkowych z rozdz.3 i 4 dotyczących tylko funkcji parzystych.
Wnioski:
1. c0=c(ω=0)≈0.0667+j0≈0.0667-składowa stała gdy n=0
2. c(-∞)=c(+∞)=0+j0–>harmoniczne dla ω=-∞ i ω=+∞ są nieskończenie małe, przyjmijmy jako zerowe.
3. c(+n)=c(-n)* są liczbami zespolonymi sprzężonymi, np. c(+1) i c(-1)*
4. Każdy c(n), czyli n-ty wektor, odpowiada harmonicznej o pulsacji n*ω0, amplitudzie A równej długości wektora i fazie φ.
Np. c(+1)=c(+1*ω0) dla ω0≈1*0.419/sek–>A≈0.0307 i ϕ=-22.72°, odpowiada harmonicznej h(+1)≈0.057cos(0.419*t)-0024*sin(0.419*t)≈0.0307*cos(0.419*t-22.72°)
Analogicznie sprzężone c(-1)=c(-1ω0) odpowiada harmonicznej h(-1)≈0.0307*cos(0.419*t+22.72°)
5. Punktów dla n=-∞…-13 oraz n=+13…+∞ nie zaznaczyłem. Gęstnieją one zbliżając się do z=0+j0 gdy ω=nω0–>+-∞.
Rozdz. 6.2.5 Interpretacja wykresu z Rys.6-5 jako Szeregu Fouriera
Te 26 współczynników c(n) na Rys.6-5, to nic innego jak Szereg Fouriera funkcji f(t). Zwłaszcza gdy wyobrazisz sobie, że wszystkie wektory poruszają się po okręgach wokół z=(0,0), każdy ze swoją prędkością +-nω0. Wektory górne “zegarowo” a dolne przeciwnie, jak na animacji Rys. 6-6. Ich suma jako f(t) zawsze będzie na osi rzeczywistej Re z, bo tworzą je pary wektorów sprzężonych, np. c(+1) i c(-1). Czyli na osi Re z pojawi się rzut sumy wszystkich wirujących wektorów, który będzie poruszał się w takt f(t) wg. wzoru na sumę z Rys. 6-3. Ta funkcja f(t) będzie oczywiście z Rys. 6-2, przy założeniu n=-∞…0…+∞.
Gdy n=-12…0…+12, czyli takie jak na Rys. 6-2, to f(t) będzie “stępione”, inaczej bez ostrych czubków. Te wirujące wektory są idealnym przykładem zespolonego wzoru na Szereg Fouriera.
Poniższa animacja przedstawia przeciwnie wirujące wektory, których suma jako f(t), porusza się tylko na osi rzeczywistej Re z.
Rys.6-6
Suma 2 przeciwnie obracających się wektorów sprzężonych
a-stan początkowy wektora c(n)
b-stan początkowy wektora sprzężonego czyli c(n)*
c-suma c(n)+c(n)*
Spójrz jeszcze raz na Rys.6-3 na wzór ze znakiem ∑.
Rzeczywistą funkcję f(t) tworzą przeciwnie wirujące pary wektorów c(n)exp(jnω0t) i c(-n)exp(-jnω0t).
Rozdz. 6.2.6 Ilorazowy Szereg Fouriera, czyli ze współczynnikami c(n)/ω0
Każdy punkt/wektor/współczynnik c(n) z Rys. 6.05 podzielimy przez ω0=Δω≈0.419*1/sek. W ten sposób, łatwiej przejdziemy z Szeregów do Transformaty Fouriera. Podobnie podzieliśmy amplitudę a(n) przez Δω na
Rys.4-2 w rozdz.4. Rysunek duży nieco, ale dzięki temu symbole +-1ω0,+-2ω0…są jeszcze czytelne.
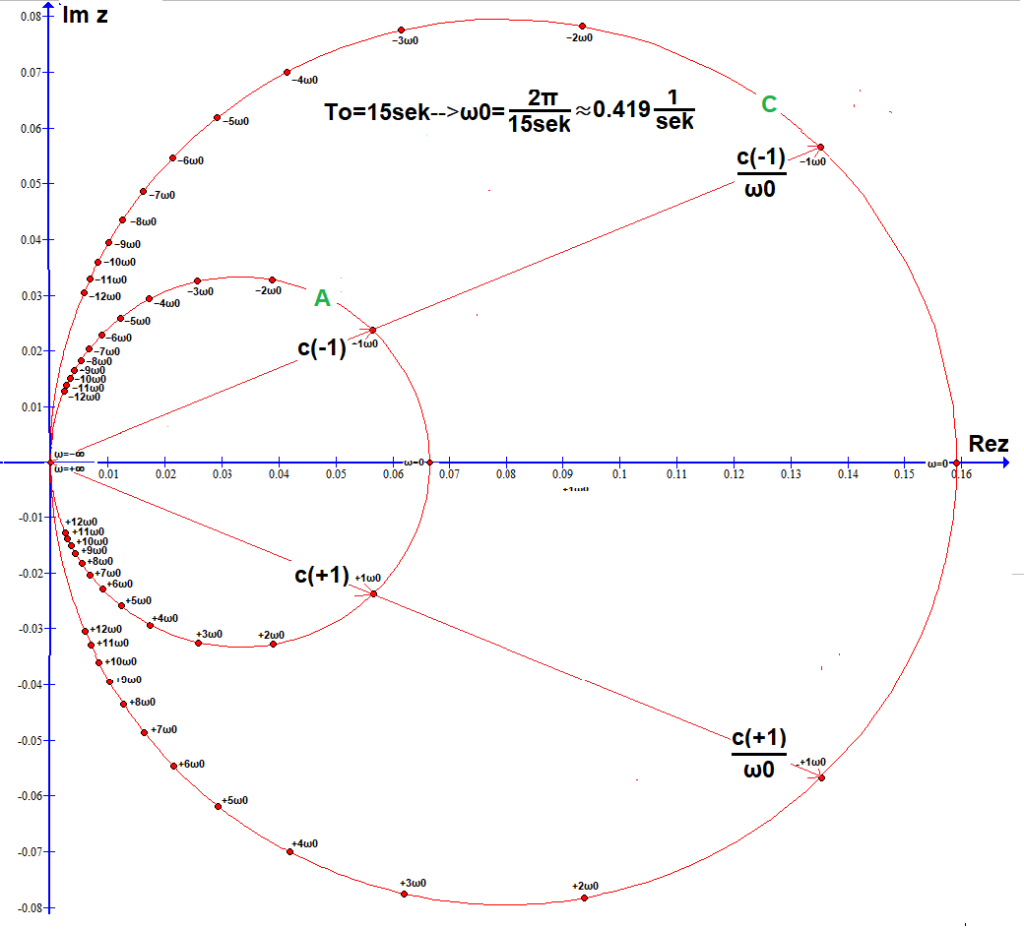
Rys.6-7
26 współczynników c(n) na okręgu A, czyli powtórzenie Rys. 6-5.
26 współczynników c(n)/ω0 na okręgu C (ω0≈0.409)
Punkty c(n) na okręgu A zostały przekształcone w punkty c(n)/ω0 na okręgu C. Po co? Bądź cierpliwy.
Rozdz. 6.3 Szereg Fouriera funkcji f(t) o okresie To=30sek
Rozdz. 6.3.1 Wstęp
Dwukrotnie zwiększymy okres To. Pulsacja ω0=2π/30sek≈0.209/sek będzie 2 razy mniejsza niż w rozdz. 6.2.
Jak się zmienią odpowiednie współczynniki/punkty c(n) i c(n)/ω0 z Rys.6-7?
Rozdz. 6.3.2 Wykres funkcji

Rys. 6-8
Funkcja okresowa f(t) okresie To=30sek
Czyli drugie i lepsze przybliżenie funkcji f(t) z Rys. 6-1. Lepsze, bo To=30sek jest bliższe To=∞ niż poprzednie To=15sek. Idziemy więc drogą z rozdz.3, w którym pojedynczy impuls prostokątny A=1 Tp=1sek, zastępowaliśmy ciągiem tych impulsów, czyli funkcjami okresowymi o zwiększającym się okresie To.
Rozdz. 6.3.3 Obliczenie zespolonych współczynników Fouriera c(n) programem Wolfram Alfa
Współczynniki Fouriera c(n) obliczymy analogicznie jak w Rozdz. 6.2. Instrukcją dla WolframaAlfa dla np. n=3 będzie:
(1/30)*integrate exp(-t)*heavisde(t)*exp(-2pi*i*3*t/30)dx from t=-15 to15
Rozdz. 6.3.4 Współczynniki c(n) na płaszczyźnie zespolonej Re z/Im z
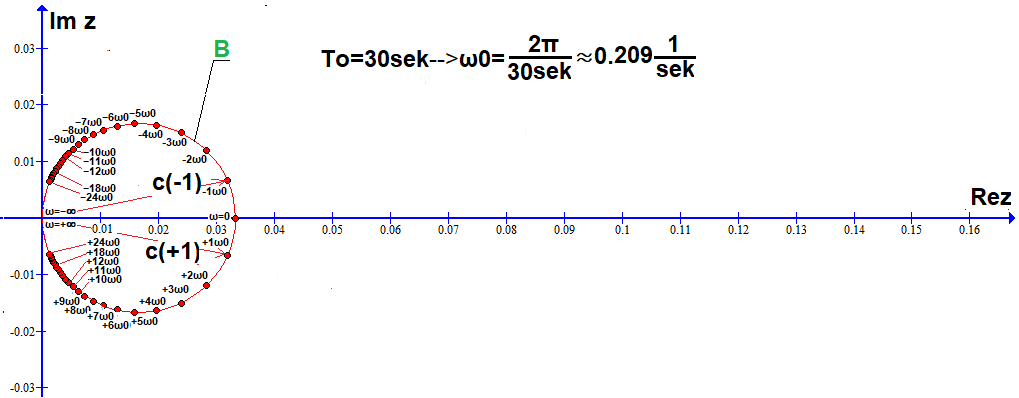
Rys.6-9
50 współczynników c(n) Szeregu Fouriera na okręgu B obliczone programem WolframAlfa.
W tym: 24 dolnych c(n), 24 górnych c(n), c(ω=0), c(ω=+∞)=c(ω=-∞)=(0,0). Porównaj z Rys.6-5 gdy To=15sek.
Wnioski:
Współczynniki c(n) są mniejsze i gęściej rozłożone na 2 razy mniejszym od A okręgu B, bo odstępy Δω=ω0≈0.209/sek między kolejnymi harmonicznymi są 2 razy mniejsze. A co by było, gdyby wektory zaczęły wirować wokół z=(0.0)? Wtedy rzut sumy tych wektorów poruszałyby się na osi Re z podobnie do f(t) z Rys. 6-8, tylko w sposób “bardziej wygładzony i bez czubków”.
Rozdz. 6.3.5 Ilorazowy Szereg Fouriera, czyli ze współczynnikami c(n)/ω0
Każde c(n) z Rys. 6.09 podzielimy przez ω0=Δω≈0.209*1/sek.
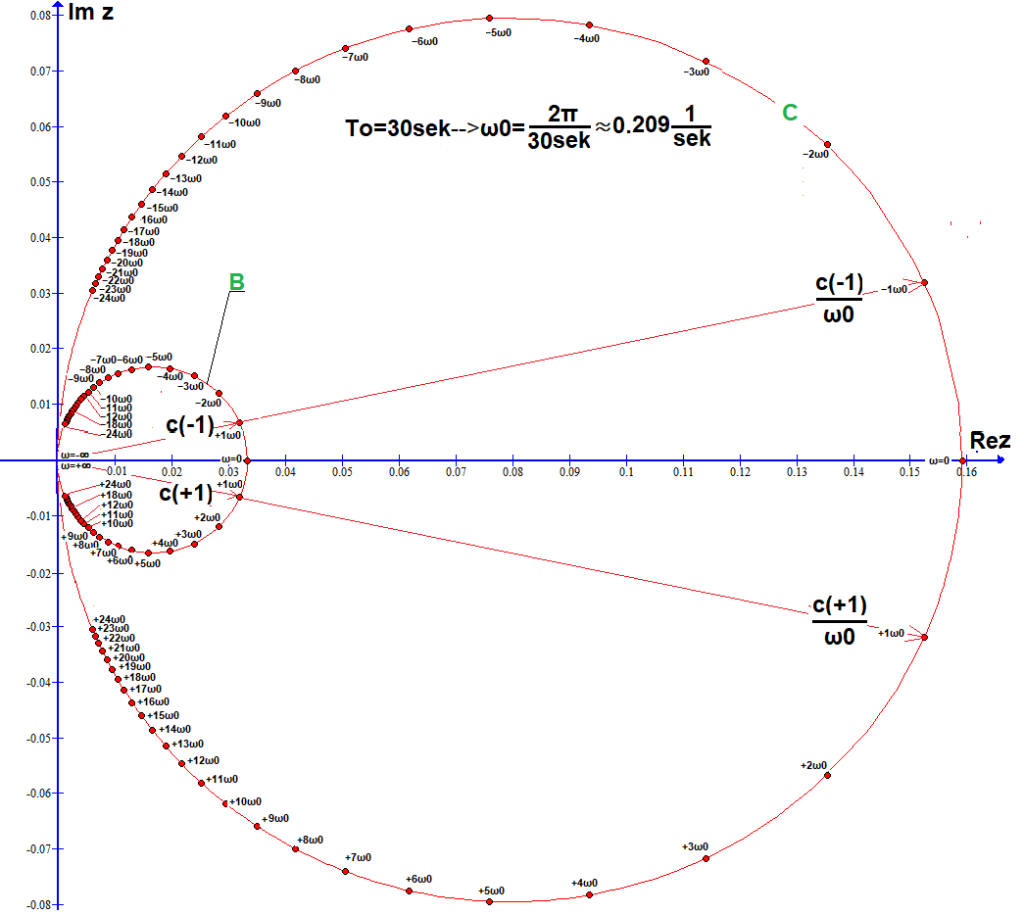
Rys.6-10
50 współczynników c(n) na okręgu B i 50 współczynników c(n)/ω0 na okręgu C (ω0≈0.209/sek)
Okrąg B jest 2 razy mniejszy od A z Rys.6-5 i Rys.6-7 i współczynniki c(n) są 2 razy gęściej rozłożone.
Okrąg C jest taki sam jak na Rys. 6-7, tylko współczynniki c(n)/ω0 są 2 razy gęściej rozłożone.
Rozdz.6.4 Co się dzieje gdy To rośnie, czyli ω0 maleje?
Rozdz.6.4.1 Wstęp
W rozdz. 6.2 było To=15sek, a w 6.3 wzrosło do To=30sek. Jaki miało to wpływ na współczynniki c(n)?
Rozdz.6.4.2 Porównanie 2 wykresów
Czyli Rys.6-7 i Rys.6-10 na jednym zbiorczym. Rysunek ma większą skalę i dlatego okręgi A,B,C są teraz mniejsze. Z jakichś powodów dodałem jeszcze okrąg D, czyli powiększony 2π razy okrąg C. Punkty c(+1)/ω0 i 2π*c(-1)/ω0 na C i D przedstawiono jako wektory. Pozostałe punkty na okręgach też są oczywiście wektorami.
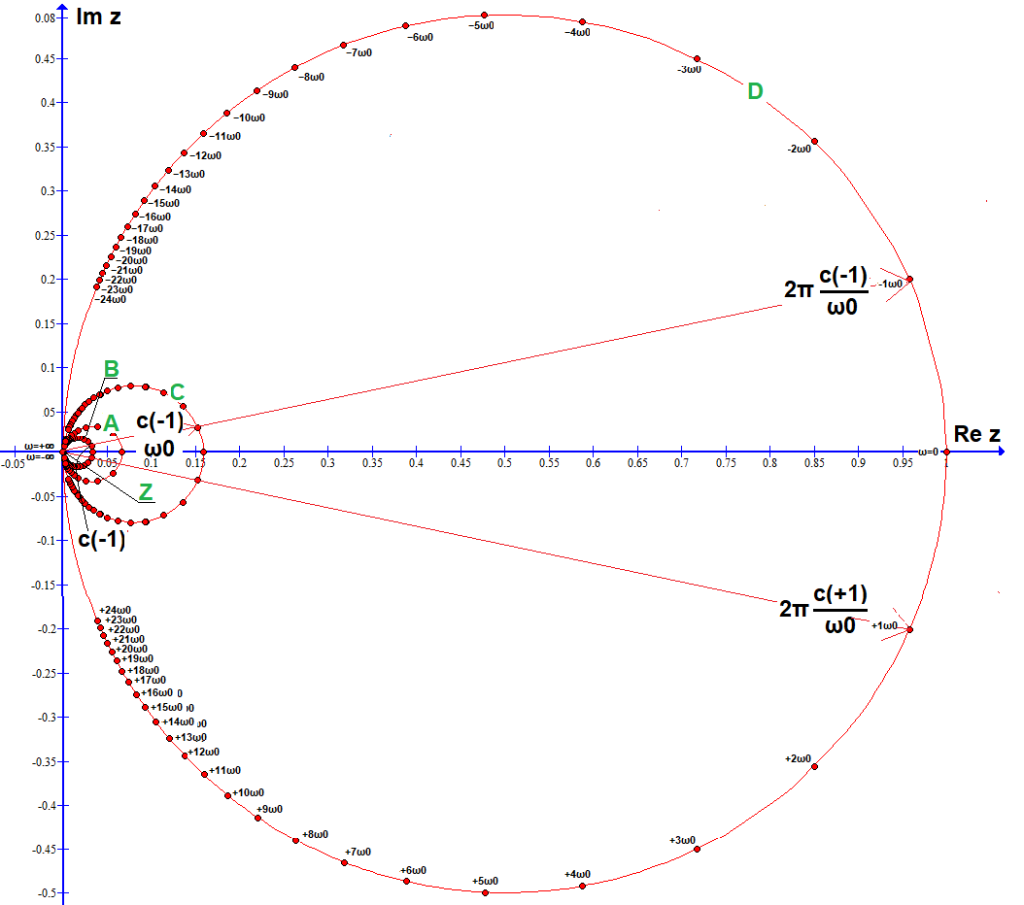
Rys. 6-11
Zespolone współczynniki c(n), c(n)/ω0 i 2π*c(n)/ω0 na okręgach A,B,C,D oraz tajemniczy “punkt-okrąg” Z sąsiadujący z (0,0).
–okrąg A z 26 punktami c(n) z Rys.6-5 gdy ω0=0.409 (To=15sek)
–okrąg B z 50 punktami c(n) z Rys.6-9 gdy ω0=0.209 (To=30sek)
–okrąg C z “ilorazowymi” punktami c(n)/ω0 z Rys.6-10:
z 26 punktami c(n) gdy ω0≈0.409 (To=15sek)
z 50 punktami c(n) gdy ω0≈0.209 (To=30sek)
Uwaga:
Chociaż okrąg B jest 2 razy mniejszy od A ale jego c(n) zostało podzielone przez 2 razy mniejsze ω0. Dlatego wszystkie punkty c(n)/ω0 od A i B są na tym samym okręgu C.
–okrąg D z punktami 2π*c(n)/ω0, czyli powiększony 2π razy okrąg C:
z 26 punktami c(n) gdy ω0≈0.409 (To=15sek)
z 50 “ilorazowymi” punktami c(n) gdy ω0≈0.209 (To=30sek)
Po co powiększenie 2π? Okaże się później. Na razie, “żeby lepiej widać”.
Wszystkie punkty na okręgach C i D pochodzą od B, ale tylko co drugi od A. Gdyby wektory na okręgach A i B zaczęły wirować z prędkościami n*ω0, to ich rzuty na oś rzeczywistą Re Z byłyby podobne do f(t) z Rys. 6-2 i 6-8, tylko bardziej stępione i “bez czubków”.
Rozdz.6.4.3 To nadal rośnie…
Analizujemy funkcję f(t) podobną do Rys.6-8, tylko “rzadszą” bo To=60sek. Co zmieniłoby się na Rys. 6-11?
1. Wewnątrz C powstałby 2 razy mniejszy od B okrąg E. Uwaga: Okręgu E oraz jego f(t) nie ma na rysunkach.
2. Okrąg E zawiera 2*48+1+1=98 punktów/współczynników c(n)
3. Na okręgach C i D pojawiłoby się 98 “potomków” E. Podobnie jak 50 “potomków” B na C i D z Rys.6-11.
Wniosek
Wraz ze wzrostem To powstają coraz mniejsze okręgi A,B,E,F,G…Z z coraz bliższymi sobie punktami c(n). Porównaj np. A i B. Ewidentnie punkty c(n) na B są “gęstsze”. Nie tylko dlatego, że B jest mniejsze od A! Także dlatego, że odstęp Δω0=ω0 między c(n) zmniejszył się dwukrotnie. Te zmniejszające się okręgi A,B,E,F,G…Z stają się coraz “bardziej ciągłe”. Aż powstanie nieskończenie mały i ciągły okrąg Z gdy To=∞. Jest nim właśnie wcześniej wspomniany tajemniczy “punkt-okrąg” Z na Rys.6-11. Tu odstępy między punktami/wektorami c(n)=c(n*dω) są nieskończenie małe (To–> ∞ czyli dω=ω0–>0).
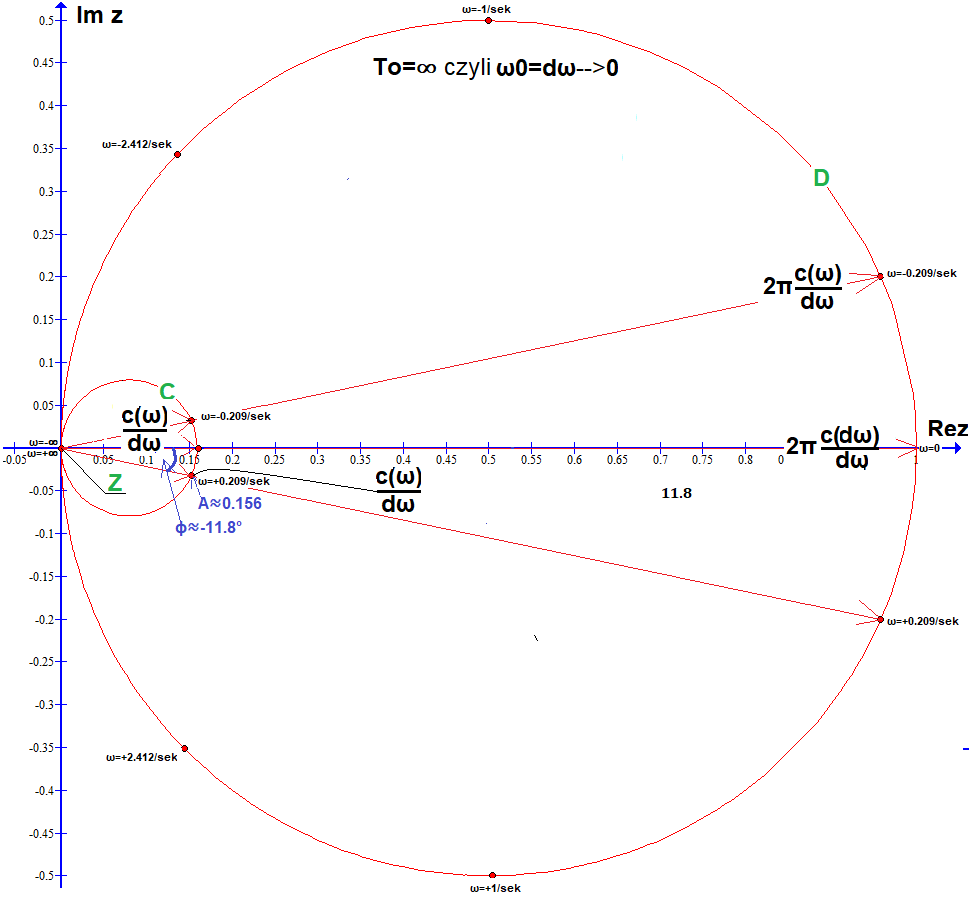
Rys. 6-12
Okręgi C i D oraz nieskończenie mały okrąg Z wewnątrz C
Te “dotykające” się punkty c(n), na nieskończenie małym i ciągłym okręgu Z są współczynnikami Szeregu Fouriera nieokresowej funkcji f(t) z Rys.6-1. Tzn. istnieje harmoniczna dla każdej ciągłej pulsacji ω, a nie tylko dla konkretnych ω=n*ω0 jak na Rys.6-7 i 6-10. Inna rzecz, że każda harmoniczna jest nieskończenie mała! Trudno coś tak małego jak Z analizować. Jeżeli współczynniki c(n) na okręgach A, B, E,…podzielisz przez odstęp Δω=ω0 między nimi (dla A–>Δω=ω0≈0.419/sek, dla B–>Δω=ω0≈0.209/sek), to punkty c(n)/ω0 znajdą się na tym samym okręgu C. Czyli okręg C o współrzędnych c(ω)/dω, to powiększone (“przez lupkę”) punkty c(ω) okręgu Z. Zaś okrąg D jako 2π*c(ω)/dω, czyli powiększony 2π razy okrąg C, jak się później okaże, jest właśnie transformatą funkcji f(t) z Rys. 6-1.
Rozdz.6.5 Czym jest Transformata Fouriera funkcji f(t) z Rys.6-1?
Rozdz.6.5.1 Wstęp
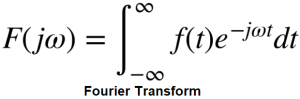
Rys. 6-13
Transformata Fouriera
Większość autorów zaczyna od tego. Nie mówi czym jest Transformata Fouriera, ale jak się ją oblicza. To tak jakby ktoś zdefiniował młotek jako produkt, który należy wykonać w w taki, a nie inny sposób. A powinno być tak. Młotek to narzędzie do wbijania gwoździ. Zaś Transformata Fouriera to wzór, który pozwala obliczyć rozkład harmonicznych w sygnale f(t).
Rozdz.6.5.1 Czym jest okrąg C o współrzędnych c(ω)/dω z Rys.6-12?
Nieskończenie mały okrąg Z składa się z punktów c(ω), których każdy jest wektorem odpowiadającym harmonicznej o pulsacji ω.
Np. dla pulsacji ω=+1/sek jest to harmoniczna o nieskończenie małej amplitudzie A i fazie φ≈-11.8º. Na razie uwierz na słowo, zwłaszcza jeśli chodzi o φ=-11.8º. Ale jeżeli powiększysz Z poprzez operację c(ω)/dω, to otrzymasz okrąg C na Rys. 6-12, na którym “więcej widać”, także φ≈-11.8º. Z tego wynika, że amplituda A harmonicznej o pulsacji np. ω=+0.209/sek funkcji chociaż jest nieskończenie mała, ale większa od tej gdy ω=+1/sek, a mniejsza od ω=0/sek. A samo wyrażenie c(ω)/dω jest gęstością harmonicznej względem pulsacji ω. Podobnie jak masa ołowiu w punkcie jest zerowa m=0, ale jego gęstość względem objętości V jest niezerowa ρ=11,34 g/cm³! Biorąc pod uwagę, że mamy do czynienia z wektorem c(ω)/dω, to potraktuj gęstość tego wektora dla ω=+0.209/sek, jako średnią jego wartość w okolicach pulsacji ω=+0.209/sek. Czyli sumujemy/całkujemy wszystkie (nieskończenie małe!) wektory np. dla ω=+0.2085/sek…ω=+0.2095/sek i dzielimy przez Δω=0.2095/sek-0.2085/sek=0.001sek. Powstanie wektor c(ω)/Δω≈0.156*exp(-j11.8º). Czyli gęstością widmową funkcji wykładniczej f(t) z Rys.6-1 dla ω=+0.209/sek jest wektor o amplitudzie A=0.156 i fazie φ≈-11.8º. A przekładając na harmoniczne, to f(t) z Rys.6-1 ma w okolicach ω=+0.209/sek harmoniczną o średniej wartości h(t)=0.156*cos(0.209t-11.8º). Nie muszę dodawać, że wartość c(ω)/dω jest najdokładniejsza gdy Δω–>dω–>0. Podobnie jak gęstość masy w punkcie ρ=m/Δv jest najdokładniejsza gdy Δv–>0.
A wracając do pytania z tytułu Rozdz.6.5.1. Okrąg C jest “prawie” transformatą funkcji f(t) z Rys.6-1. A już “nie prawie” tylko “dokładnie”, to Transformatą Fouriera funkcji f(t) jest okrąg D na Rys. 6-12. Dlaczego? Patrz Rozdz.6.5.2.
Rozdz.6.5.2 Więcej o Transformacie Fouriera
Już wiesz, że Transformatą Fouriera funkcji f(t) jest zespolona funkcja F(jω) w postaci okręgu D na na Rys. 6-13. A innych funkcji, ściślej takich których pole pod funkcją f(t) jest skończone? Czyli dowolnych, choć nie do końca. Wyobraź sobie, że jest to trochę inna funkcja niż f(t) z Rys. 6-1, ale nieokresowa i o skończonym polu. Nie może być nią jednak np. f(t)=exp(t).
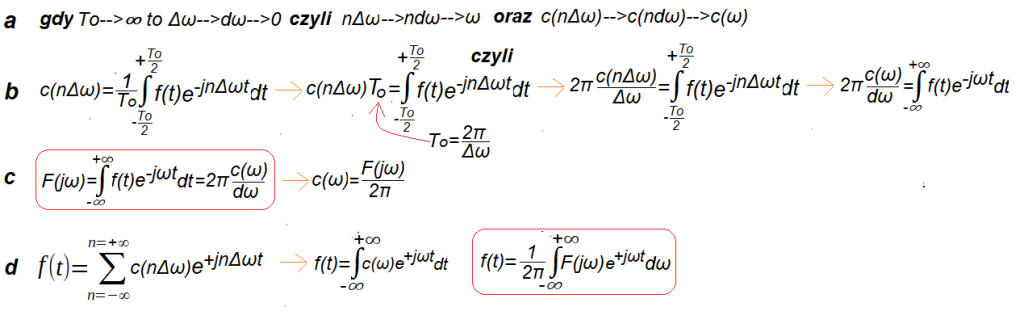
Rys. 6-14
a. Co się dzieje gdy okres To funkcji f(t) dąży do nieskończoności?
Wtedy pierwsza harmoniczna ω0=Δω dąży do nieskończenie małego dω. Oznacza to też, że odstępy dω między kolejnymi harmonicznymi są nieskończenie małe. Innymi słowy kolejne harmoniczne “zachodzą na siebie” i ich rozkład c(n*dω) staje się ciągły c(ω).
b. c(nΔ) jest n-tą amplitudą zespoloną gdy f(t) jest przybliżeniem okresowym f(t) dla skończonego To. Gdy To=∞ to c(ω)/dω staje się ciągłe a 2π*c(ω)/dω jest właśnie Transformatą Fouriera F(jω) funkcji f(t)!
c. Ostateczny wzór na na Transformatę Fouriera F(jω). Zauważ, że jest ona powiększoną przez 2π gęstością widmową c(ω)/dω.
d. Gdy przybliżeniem nieokresowej f(t) jest okresowa (o dużym okresie To!) to f(t) jest zwykłym wzorem na Szereg Fouriera z lewej strony. A gdy To–>∞ to wzór na Szereg Fouriera staje się ciągłym wzorem na tzw. Odwrotną Transformatę Fouriera. Pozwala ona obliczyć przebieg f(t) na podstawie jej Transformaty Fouriera F(jω).
Rozdz.6.6 Transformata Fouriera i Odwrotna Transformata Fouriera.
Czyli ostateczne podsumowanie rozdziału
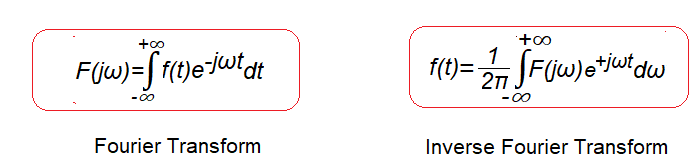
Rys. 6-15
Transformata Fouriera i Odwrotna Transformata Fouriera
Jedna z bardziej znanych par równań matematycznych. Wypada je znać, nawet jeżeli nie są zrozumiałe do końca.
