Wirujące Szeregi Fouriera
Rozdział 5 Jak odfiltrować harmoniczną z
f(t)=1.3+0.7*cos(2t)+0.5*cos(4t)?
Rozdział 5.1 Wstęp
W poprzednim rozdziale wyłuskaliśmy harmoniczną 0.5*cos(4t) z funkcji f(t)=0.5*cos(4t) i z funkcji f(t)=0.5*cos(4t-30°) przy pomocy wirującej z prędkością ω=n*ω0 płaszczyzny Z. Teraz zrobimy to samo, ale z funkcją f(t)=1.3+0.7*cos(2t)+0.5*cos(4t). Pulsacje obu cosinusów są różne! Ciekawe, jak to wpłynie na wykres f(t) i wirujące trajektorie f(jnω0t)?
Przekonasz się że:
– niezależnie od pulsacji nω0, okresem trajektorii F(jnω0t) jest T=6.28 sek
– dla ω=0*ω0=0/sek funkcja nie wiruje!
– dla ω=1*ω0=1/sek…8*ω0=8/sek promień R=1 wykona 1…8 obrotów
Czy uda się wyłuskać składową stałą c0=1.3 oraz harmoniczne h2(t)=0.7*cos(2t) i h4(t)=0.5*cos(4t)?
Rozdział 5.2 Trajektoria F(0j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-0j1t) czyli bez wirowania
Problem podobny do Rys. 4-2 poprzedniego rozdziału. Promień R nie wiruje, ale zmienia się wg. funkcji okresowej R(t)=f(t)=1.3+0.7*cos(2t)+0.5*cos(4t). Czyli trajektorią na płaszczyźnie zespolonej Z jest
F(0j1t)=f(t)*exp(-j0)=f(t)=1.3+0.7*cos(2t)+0.5*cos(4t). Przy okazji zobaczysz wykres funkcji f(t).
Rys. 5-1
Funkcja F(0j1t)=f(t)=1.3+0.7*cos(2t)+0.5*cos(4t) w wersji zespolonej i rzeczywistej
Rys. 5-1a
F(0j1t)=f(t)=1.3+0.7*cos(2t)+0.5*cos(4t) w wersji zespolonej
Rys. 5-1b
F(0j1t)=f(t)=1.3+0.7*cos(2t)+0.5*cos(4t) w wersji rzeczywistej
Wniosek.
Średnią wartością f(t) w okresie T=2π≈6.28sek (a także T=πsek≈3.14sek) jest c0=1.3.
Jest to także środek ciężkości sc0=(1.3,0) “bujającej” się trajektorii na Rys.5-1a, gdy prędkość wirowania płaszczyzny ω=0. Inna nazwa parametru c0=1.3 to składowa stała funkcji f(t).
Uwaga.
W Szeregu Fouriera funkcji okresowej f(t) pierwszym elementem jest składowa stała– współczynnik c0=a0. Jest to średnia f(t) w okresie T.
Liczymy go jako jako całkę z poniższego wzoru.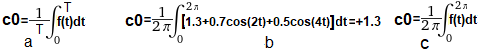
Rys.5-2
Wzór na składową stałą funkcji okresowej f(t), czyli na c0
Jest to średnia funkcji f(t) w okresie T
Rys.5-2a
Wzór ogólny dla f(t) o okresie T
Rys.5-2b
Wzór dla f(t)=1.3+0.7*cos(2t)+0.5*cos(4t) i T=2π
Rys.5-2c
Wzór dla dowolnego f(t) i T=2π
Rozdział 5.3 Trajektoria F(1j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-1j1t) czyli z wirowaniem -1ω0=-1/sek
Promień R=1 wiruje z -1ω0=-1/sek.
Spójrz na animację z Rys.5-1a. Koniec wektora porusza się “wte i we wte” wokół c0=(+1.3, 0) wg. wzoru R(t)=f(t)=1.3+0.7*cos(2t)+0.5*cos(4t). A gdyby wektor zaczął wirować z prędkością -1ω0=-1/sek? Czyli “zegarowo” i z okresem T≈6.28sek. Wtedy jego ruch na płaszczyźnie zespolonej Z jest opisany jest funkcją zespoloną F(1j1t).
Rys.5-3
F(1j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-j1t)
Animacja trwa T=2π/ω0≈6.28sek.
Rys.5-3a
Promień R=0.5 z 1ω0=1/sek wykona 1 obrót.
Zauważ, że jako wzorcowy stały promień wybraliśmy R=0.5. Także w w następnych animacjach
Rys.5-3b
W czasie obrotu zmienia się długość promienia zgodnie z funkcją R(t)= f(t)=1.3+0.7*cos(2t)+0.5*cos(4t).
Realizowana jest więc funkcja zespolona jako wirujący wektor F(1j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-j1t)
Rys.5-3c
Funkcja zespolona F(1j1t) jako trajektoria.
Rysowana jest przez wektor z Rys.5-3b
Środkiem ciężkości trajektorii F(1j1t) jest ewidentnie sc1=(0,0)=0. Czyli funkcja f(t) nie ma harmonicznej o pulsacji 1ω0=1/sek.
Rozdział 5.4 Trajektoria F(2j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-2j1t) czyli z wirowaniem -2ω0=-2/sek
Rys.5-4
F(2j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-2j1t)
Animacja trwa T≈6.28sek.
Rys. 5-4a
Promień R=0.5 wykona 2 obroty.
Rys.5-4b
Funkcja zespolona F(2j1t) jako wirujący wektor.
Wektor R(t) o zmiennej długości wykona 2 obroty.
Rys.5-4c
Funkcja zespolona F(2j1t) jako trajektoria.
Drugi obrót po tym samym torze. Środkiem ciężkości trajektorii jest teraz sc2=(0.35,0). Jest to wektor i można go też zapisać w postaci wykładniczej zespolonej sc2=R*exp(jϕ)=0.35*exp(j0°). W Rozdziale 7 dowiesz się, ze środka ciężkości trajektorii można łatwo odczytać 2 harmoniczną funkcji f(t) jako h2(t)=0.7cos(2t). Spójrz na f(t). Zgadza się!
Uwaga.
Nie wnikaj jak obliczyliśmy środek ciężkości sc2=(0.35,0). Na razie zaufaj intuicji, chociaż wydaje się, że powinien być ciut bardziej przesunięty w prawo. Zauważ jednak, że prędkość lewej strony trajektorii jest trochę mniejsza. Czyli odległości od sc2 będą trochę gęściej rozmieszczone, niż po prawej stronie. Tak jakby tu trajektoria była rysowana grubszą linią.
Rozdział 5.5 Trajektoria f(3j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-3j1t) czyli z wirowaniem -3ω0=-3/sek
Rys.5-5
F(3j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-3j1t)
Animacja trwa T≈6.28sek.
Rys. 5-5a
Promień R=0.5 wykona 3 obroty.
Rys.5-5b
Funkcja zespolona F(3j1t) jako wirujący wektor
Rys.5-5c
Funkcja zespolona F(3j1t) jako trajektoria.
Środkiem ciężkości trajektorii F(3j1t) jest sc3=(0,0)=0. Czyli funkcja f(t) nie ma harmonicznej o pulsacji 3ω0=3/sek.
Rozdział 5.6 Trajektoria F(4j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-4j1t) czyli z wirowaniem -4ω0=-4/sek
Rys.5-6
F(4j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-4j1t)
Animacja trwa T≈6.28sek.
Rys. 5-6a
Promień R=0.5 wykona 4 obroty.
Rys.5-6b
Funkcja zespolona F(4j1t) jako wirujący wektor.
Wektor R(t) o zmiennej długości wykona 4 obroty.
Rys.5-6c
Funkcja zespolona F(4j1t) jako trajektoria.
3 i 4 obrót po tym samym torze. Niezerowy środek ciężkości sc4=(0.25,0)!
Ze środka ciężkości sc4 można odczytać 4 harmoniczną funkcji f(t) jako 0.5cos(4t).
Rozdział 5.7 Wirujący promień 5ω0=5/sek, czyli trajektoria F(j5ω0t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-j5ω0t) dla 5ω0=5/sek.
Rys.5-7
F(j5ω0t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-j5t)
Animacja trwa T≈6.28sek.
Rys. 5-7a
Promień R=0.5 wykona 5 obrotów.
Rys.5-7b
Funkcja zespolona F(5j1t) jako wirujący wektor
Rys.5-7c
Funkcja zespolonaF(5j1t) jako trajektoria.
Środkiem ciężkości trajektorii F(5j1t) jest sc5=(0,0)=0. Czyli funkcja f(t) nie ma harmonicznej o pulsacji 5ω0=5/sek.
Rozdział 5.8 Trajektoria F(6j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-6j1t) czyli z wirowaniem -6ω0=-6/sek
Rys.5-8
F(6j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-j2t)
Animacja trwa T≈6.28sek.
Rys.5-8a
Promień R=0.5 wykona 6 obrotów.
Rys.5-8b
Funkcja zespolona F(6j1t) jako wirujący wektor
Rys.5-8c
Funkcja zespolona F(6j1t) jako trajektoria. 4..6 obrót po tym samym torze, dlatego pozornie zatrzymała się.
Środkiem ciężkości trajektorii f(6j1t) jest sc6=(0,0)=0*. Czyli funkcja f(t) nie ma harmonicznej o pulsacji 6ω0=6/sek.
*sc6=(0,0) nie jest tak oczywiste jak np. dla Rys.5-7c. Wydaje się za bardzo przesunięty w lewo. Zauważ jednak, że prędkości trajektorii po lewej stronie są mniejsze niż po prawej.
Rozdział 5.9 Trajektoria F(7j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-7j1t) czyli z wirowaniem -7ω0=-7/sek
Rys.5-9
F(7j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-7j1t)
Funkcja zespolona f(j7ω0t) dla 7ω0=7/sek.
Animacja trwa T≈6.28sek.
Rys. 5-9a
Promień R=0.5 wykona 7 obrotów.
Rys.5-9b
Funkcja zespolona F(7j1t) jako wirujący wektor
Rys.5-9c
Funkcja zespolona F(7j1t) jako trajektoria.
Środkiem ciężkości trajektorii F(7j1t) jest sc7=(0,0)=0. Czyli funkcja f(t) nie ma harmonicznej o pulsacji 7ω0=7/sek.
Rozdział 5.10 Trajektoria F(8j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-8j1t) czyli z wirowaniem -8ω0=-8/sek
Rys.5-10
F(8j1t)=[1.3+0.7*cos(2t)+0.5*cos(4t)]*exp(-8j1t)
Animacja trwa T≈6.28sek. f(j8ω0t).
Rys. 5-10a
Promień R=0.5 wykona 8 obrotów.
Rys.5-10b
Funkcja zespolona F(8j1t) jako wirujący wektor.
Rys.5-10c
Funkcja zespolona F(8j1t) jako trajektoria.
Środkiem ciężkości trajektorii F(8j1t) jest sc8=(0,0)=0. Czyli funkcja f(t) nie ma harmonicznej o pulsacji 8ω0=8/sek.
