Transformata Fouriera
Rozdz. 4 Transformata Fouriera pojedynczego impulsu prostokątnego cz. 2
Rozdz. 4.1 Szeregi Fouriera ciągów impulsów prostokątnych A=1 Tp=1sek przy zwiększającym się okresie To.
Rys. 4-1
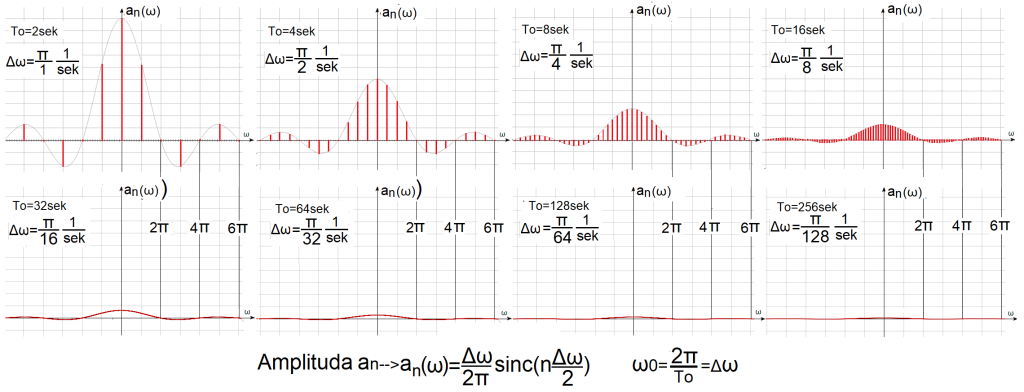
Szeregi Fouriera ciągów impulsów prostokątnych A=1 Tp=1sek jako wykresy prążkowe.
Jest to graficzne podsumowanie rozdz. 3, w którym impulsy A=1 T=1sek stają się coraz rzadsze. Wzór na n-ty prążek an(ω), czyli na amplitudę n-tej harmonicznej i wykresy prążkowe przedstawiają to samo. Górne wykresy prążkowe “bujały” się w rozdz. 3 jako animacje na Rys. 3-7…10. Największe prążki to środkowe składowe stałe a(0). Pierwsze prawe prążki od a(0) to a(+1) a pierwsze lewe to a(-1) i dotyczą pierwszych harmonicznych dla pulsacji +,–. Prążki dolnych wykresów są już tak gęste, że wyglądają jak czerwone obwiednie.
Wnioski:
“Lewy górny” rozkład harmonicznych dotyczący fal o okresie To=2sek i impulsie A=1, Tp=1sek (czyli gęstych impulsów),składa się z rzadko rozłożonych harmonicznych o dużych amplitudach a(n).
“Prawy dolny” rozkład harmonicznych dotyczący fal o okresie To=256sek i impulsie A=1,Tp=1sek (czyli rzadkich impulsów), składa się z gęsto rozłożonych harmonicznych o małych amplitudach a(n).
A z czego składałaby się się fala prostokątna o nieskończonym okresie To i impulsie A=1 i Tp=1sek, czyli pojedynczy impuls?
Na czuja będą to nieskończenie małe harmoniczne a(n) o nieskończenie mało różniących się pulsacjach Δω–>dω–>0. Czyli dyskretny wzór na amplitudę an kolejnej harmonicznej an=a(n*Δω) stanie się funkcją ciągłą a=a(ω). Każdej pulsacji ω będzie przyporządkowana jakaś amplituda, a nie tylko dla pulsacji ω=n*Δω. Inna rzecz, że amplitudy są wtedy nieskończenie małe, ale niezerowe! Najbliżej takiej sytuacji jest wykres prążkowy dla To=256 sek. Tu To jest “prawie” nieskończonością. Te coraz bardziej płaskie wykresy a(n*Δω) coś nam chcą powiedzieć, ale co? Odpowiedzią na takie pytania jest Transformata Fouriera, służąca do badania harmonicznych pojedynczego impulsu, a ogólnie- funkcji nieokresowych.
Rozdział 4.2 Jak przejść z Szeregu Fouriera na Transformatę Fouriera?
Na razie transformata tylko dla konkretnego pojedynczego impulsu.
Z Rys. 4-1 wynika, że wykresy stają się:
– bardziej gęste-odstępy między kolejnymi a(n) maleją
– bardziej “płaskie”
Podziel więc an(ω) z Rys. 4-1 przez Δω, to otrzymasz wersję ilorazową. Zniknie wada “płaskie” i kolejne wykresy będą tak wyglądać. Wartość ω stanie się ciągła gdy Δω–>dω–>0 ω=n*dω. Bo wtedy dla każdego ciągłego ω istnieje takie n i dω, że ω=n*dω.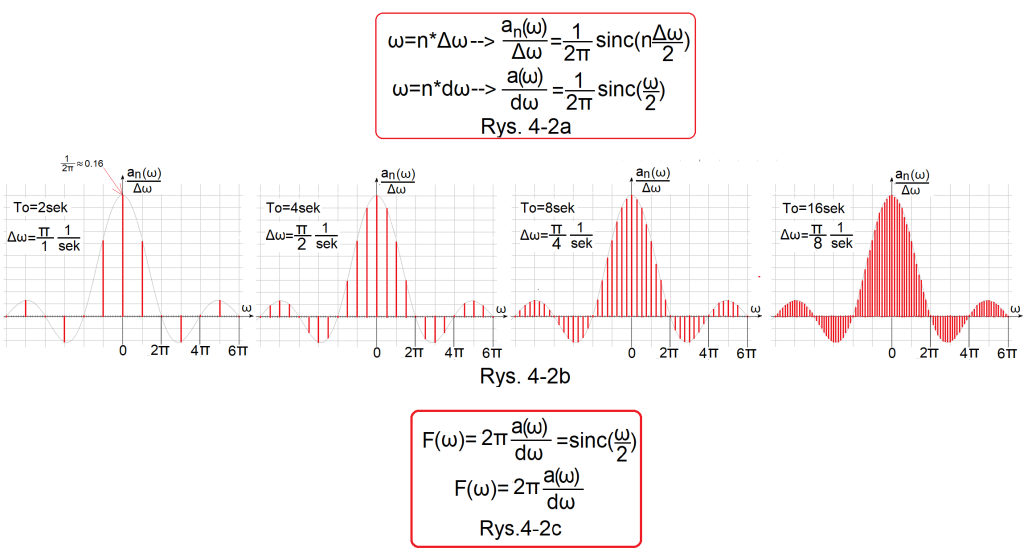
Rys. 4-2a
Iloraz an(ω)/Δω, gdy Δω jest konkretną skończoną wartością, jest funkcją dyskretną tzn. istnieje tylko dla konkretnych ω=n*Δω.
Iloraz an(ω)/dω, gdy dω jest nieskończenie małe, jest funkcją ciągłą, tzn. istnieje dla dowolnych ω. Dla każdego n i dω istnieje dowolne (ciągłe) ω takie, że ω=n*dω
Rys. 4-2b
Wyniki kolejnych 4 “Ilorazowych” wersji Szeregu Fouriera fal prostokątnych w wersji graficznej.
Ilorazy an(ω)/Δω dla f(t) impuls A=1, Tp=1sek przy zwiększających się okresach To=2, 4, 8 i 16 sek.
Rys. 4-2c
Jest to właściwie powtórzenie Rys. 4-2a, w którym zdefiniowano transformatę F(ω) pojedynczego impulsu prostokątnego x(t) jako gęstość amplitudy a(ω) względem pulsacji ω (pomnożonej przez 2π). Tu x(t) jest pojedynczym impulsem prostokątnym “startującym” w jego środku–>Rys.3-1a, ale dotyczy to wszystkich pojedynczych impulsów x(t) będących funkcjami parzystymi. W rozdz.5 uogólnimy ten wzór na wszystkie funkcji x(t), niekoniecznie parzystych.
Wnioski:
1. Obwiednia każdego wykresu jest taka sama! Tzn. jego maksimum a0/ω0=1/2π≈0.16 i miejsca zerowe ω=0,+/-2π,+/-4π,+/-6π… są dla każdego szeregu takie same. “Takie coś” łatwiej analizować niż coraz bardziej płaskie amplitudy z Rys. 4-1.
2. Kolejne “Ilorazowe” Szeregi Fouriera są “gęstsze”, bo odstępy Δω=ω0 pomiędzy kolejnymi amplitudami a(n) i a(n+1) zmniejszają się.
3. Odpowiedniki 4 dolnych–>”płaskich” z Rys. 4-1 musisz sobie wyobrazić. Będą podobne do Rys. 4-2a, tylko bardziej “gęste”.
4. A teraz najważniejsze. Powyższe wersje “ilorazowe”, nazwijmy je an/Δω są funkcjami dyskretnymi, inaczej nieciągłymi. Czyli istnieją tylko dla ω=n*Δω a nie dla dowolnego ω! A kiedy staną się funkcjami ciągłymi? Czyli obwiednią tych prążków? Wtedy gdy Δω stanie się nieskończenie małe, czyli gdy Δω–>dω tak jak na Rys. 4-2a.
Rozdział 4.3 Interpretacja Transformaty Fouriera F(ω) dla impulsu f(t)=A=1 Tp=1sek
Bo jest najłatwiejsza dla tej konkretnej funkcji f(t). Wszystkie jej harmoniczne startują w tej samej fazie φ=0 np. dla ω=1π/sek lub φ=-180º np. dla ω=1π/sek–>Rys. 4-3c. Dlatego można użyć klasycznych wykresów f(x), czego nie można powiedzieć o dowolnym impulsie, którego harmoniczne mają różne fazy początkowe φ. O takich transformatach porozmawiamy w Rozdziale 5.
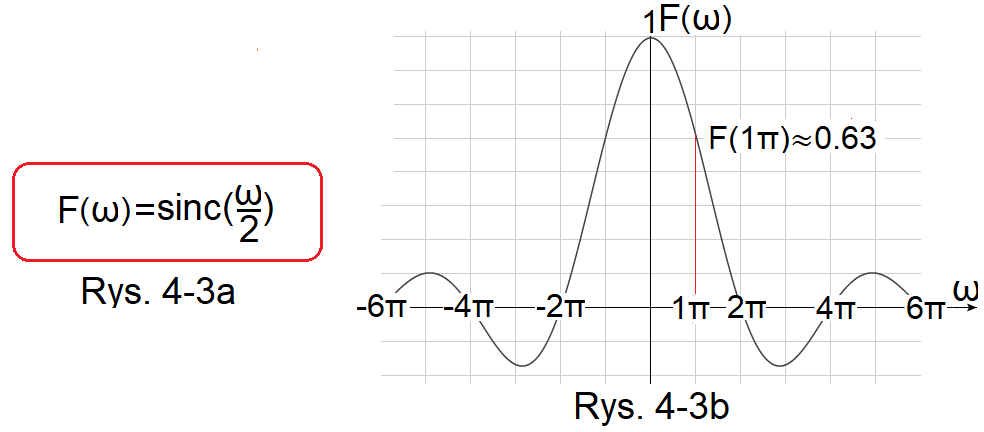
Rys. 4-3
Transformata F(ω) impulsu prostokątnego A=1 i Tp=1sek (“startującej w środku”)
Rys. 4-3a
Wzór na transformatę F(ω)
Rys. 4-3b
Wykres F(ω) tej transformaty
Jak go traktować? Np. F(ω=1π/sek)≈0.63. Czy to oznacza, że dla ω=1π/sek amplituda tej harmonicznej równa się 0.63? Nieee! Przecież ten impuls składa się z nieskończenie małych nieskończenie mało różniących się pulsacją harmonicznych. Czyli harmoniczna A(ω=1π/sek)=0. Ale suma/całka tych harmonicznych w małym przedziale np. Δω=0.9999π…1.0001π już nie będzie zerowa!
Rozdział 4.4 Czym jest transformata Fouriera?
1. Transformata jest informacją o rozkładzie częstotliwości w danym sygnale.
2. Czyli jest funkcją pulsacji F(ω).
3. Jest przeważnie funkcją zespoloną F(ω). Będzie o tym mowa w Rozdziale 5. Na szczęście nasz impuls A=1, Tp=1sek jest funkcją parzystą, a transformaty funkcji parzystych są “łatwiejszymi”, bo rzeczywistymi, funkcjami F(ω). Dlatego możemy przedstawić ją w formie wzoru Rys. 4-3a lub wykresu Rys. 4-3b.
Rozdział 4.4 Pręt i transformata
Analogie ułatwią zrozumienie idei transformaty.
Zwłaszcza to, że harmoniczna A(ω) dla pulsacji ω jest zerowa, ale transformata F(ω) dla pulsacji ω jest niezerowa.
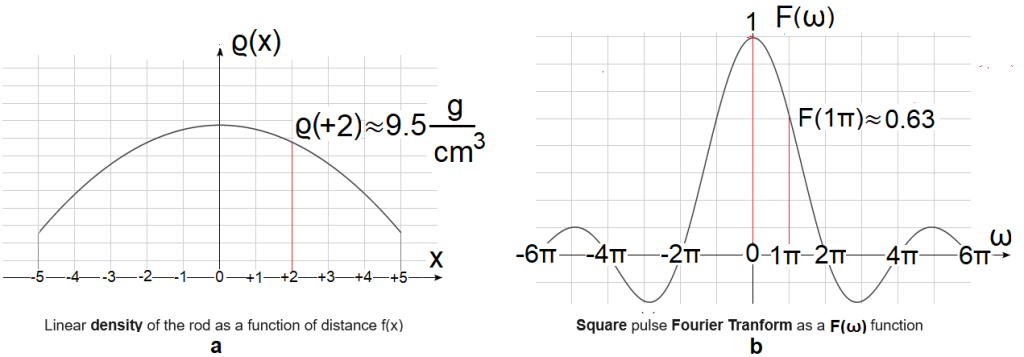
Rys. 4-4
Gęstość masy pręta ϱ(x) a transformata impulsu prostokątnego F(ω).
Rys. 4-4a
Masa pręta w dowolnym przekroju x jest zerowa bo objętość każdego przekroju ΔV=0.
Gęstość pręta ϱ(x) w dowolnym przekroju x nie jest zerowa.
Pręt ze stopu ołowiu i aluminium o przekroju s=1cm2 i długości l=10m. Gęstość liniowa pręta jest najmniejsza na krańcach -5m +5m i największa w środku. Innymi słowy na krańcach jest samo aluminium, w środku sam ołów, a w reszcie stop o składzie pośrednim. Np. ϱ(x=+2)≈9.5g/cm3
Rys. 4-4b
Amplituda harmonicznej A(ω) dla dowolnej pulsacji ω jest nieskończenie mała, przyjmijmy, że zerowa.
Gęstość amplitudy względem ω, czyli “prawie” transformata F(ω) bo F(ω)=2π*a(ω)/dω, jest niezerowa. Np. F(1π/sek)≈0.1. Oznacza to, że średnia wartość amplitudy a(ω=1π/sek) w “malutkim” zakresie ω=1π/sek-dω…1π/sek+dω to przybliżeniu 0.1. Średnia wartość czegoś w pewnym “malutkim” zakresie ω to inaczej gęstość czegoś względem ω.
