Transformata Fouriera
Rozdz. 3 Transformata Fouriera pojedynczego impulsu prostokątnego cz. 1
Rozdz.3.1 Wstęp
Trudno o prostszą funkcję nieokresową f(t) niż pojedynczy impuls prostokątny z Rys. 3-1a. Jest funkcją parzystą o amplitudzie A=1 i czasie trwania Tp=1sek. Transformata Fouriera jest ogólnie funkcją zespoloną. Ale dzięki parzystości funkcji f(t), jej transformata Fouriera F(ω) jest też funkcją rzeczywistą. A ta jest łatwiejsza do analizy niż funkcja zespolona. Przypominam, że każda funkcja i liczba rzeczywista jest zespoloną, ale nie odwrotnie! Ze względu na obszerność, temat został podzielony na rozdz. 3 i 4.
Rozdz.3.2 Pojedynczy impuls prostokątny jako sygnał o okresie nieskończonym okresie To=∞.
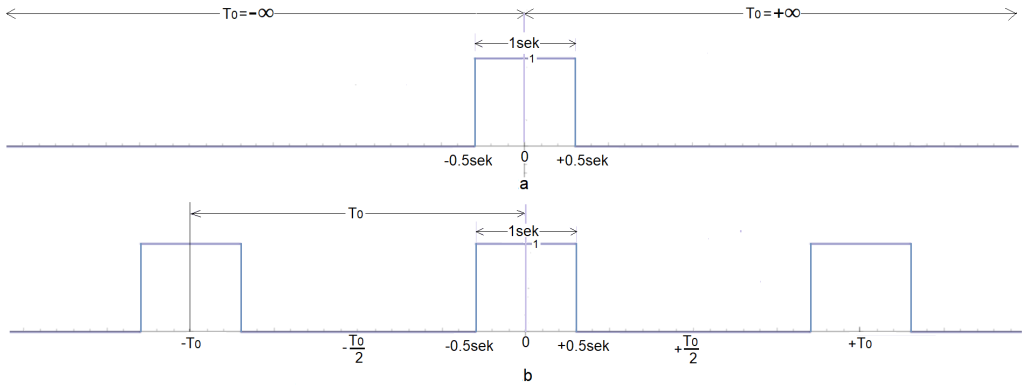
Rys. 3-1
a. Pojedynczy impuls prostokątny
– amplituda A=1
– czas trwania Tp=1sek
Impuls jest funkcją parzystą.
b. Funkcja okresowa jako ciąg impulsów o okresie To, czasie trwania Tp=1sek i amplitudzie A=1.
Pojedynczy impuls prostokątny a może być traktowany jak funkcja okresowa b o nieskończenie długim okresie To=∞.
Rozdz.3.3 Fale prostokątne o zwiększającym się okresie To.
Zbadamy kilka fal prostokątnych o różnych To ale o takiej samej amplitudzie A=1 i czasie trwania Tp=sek.
Rys. 3-2
Funkcje okresowe z impulsem A=1, Tp=1sek i zwiększającym się okresie To
a. To=2 sek –>ωo=1π/sek
b. To=4 sek–>ωo=1π/2sek
c. To=8 sek–>ωo=1π/4sek
d. To=16 sek–>ωo=1π/8sek
Fale 2,4,8,16 sek są coraz bardziej są podobne do pojedynczego impulsu. A najbardziej to To=16sek. Możemy więc obliczyć ze znanych wzorów współczynniki a(n) i b(n) Fouriera dla tej fali i powiedzieć, że “prawie” rozbiliśmy na harmoniczne “pojedynczą” f(t) z Rys.6- 1a.
Uwaga:
Impulsy powinny być zsynchronizowane. Na animacji są “prawie”.
Rozdz.3.4 Z jakiego wzoru będziemy korzystać przy wykresach prążkowych?
Wykres prążkowy dotyczy tylko funkcji parzystych i jest najbardziej intuicyjną wersją Szeregu Fouriera. Zbadamy wpływ zwiększającego się okresu To z Rys. 3-2 na wykres prążkowy. Ułatwi nam to zrozumienie idei Transformaty Fouriera, jako “potomka” Szeregu Fouriera.
Zaczniemy od ogólnego wzoru trygonometrycznego.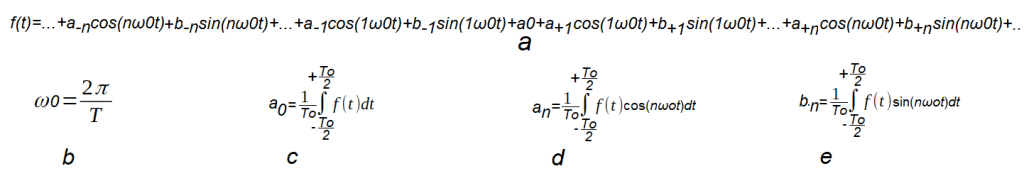
Rys. 3-3
Trygonometryczny wzór Fouriera dla dowolnej funkcji o okresie To.
W wersji zespolonej cn=an-jbn.
Uwaga:
Przedziałem całkowania we wzorach c,d,e jest -To/2…+To/2. Może być też inny, np. 0…To lub -To/4…+To3/4, pod warunkiem, że jego długością jest To.
Dla funkcji f(t) parzystej nie istnieją składowe bn i wzór uprości się.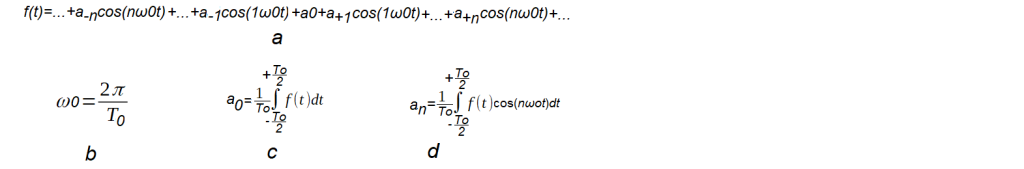
Rys. 3-4
Trygonometryczny wzór Fouriera dla parzystej funkcji okresowej f(t).
Wszystkie prążki, animacje w tym i następnym rozdziale będą związane z powyższym wzorem. Wyspecjalizujemy go jeszcze bardziej dla fali prostokątnej f(t) o czasie trwania Tp=1sek i amplitudzie A=1. Opłaca się, bo będzie dużo powtarzalnych rachunków. Okres fali To zmienia się od 2 sek do ∞ przy stałym czasie trwania Tp=1sek impulsu. Czyli wypełnienie zmniejsza się od 50% do 0%.
Rys. 3-5
Wzory na Szereg Fouriera dla fali prostokątnej z Rys. 3-1b dla różnych To, czyli różnych ω0=2π/To.
Wyprowadzenie wzorów na Rys 3-11.
Dotyczą fal prostokątnych w których:
– impuls prostokątny ma stałą wartość A=1 i Tp=1sek.
– zwiększa się tylko okres występowania tych impulsów To.
Dzięki nim łatwo wyznaczymy współczynniki an konieczne do animacji wykresów prążkowych.
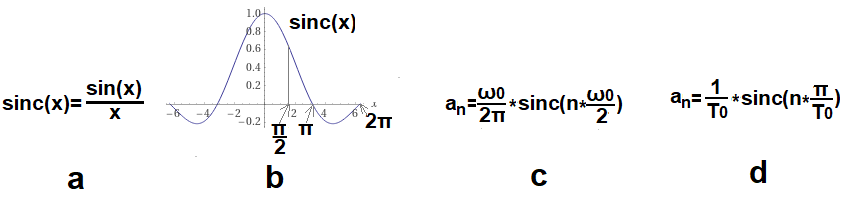
a. Definicja funkcji sinc(x) .
Funkcja f(x)=sin(x)/x tak często pojawia się w teorii sygnałów, że stworzono dla niej specjalną nazwę sinc(x). Zauważ, że chociaż co okres T=π funkcja się zeruje, to nie jest okresowa! Dąży do 0 gdy x–>+/-∞ i sinc(0)=1 jest jej maksimum. W pierwszej chwili jest to trochę dziwne, bo mamy dzielenie przez 0! Ale jest działanie typu “0/0”–>reguła de l’Hospitala i wszystko jest lege artis.
b. Wykres funkcji sinc(x)
Pokazano punkty charakterystyczne x=π/2, π i 2π
Z wykresu wynika np. że:
– sinc(0)=1
– sinc(1π)=sinc(2π)=…sinc(nπ)=0
– sinc(+∞)= sinc(-∞)=0
c. Wzór na an w funkcji pulsacji ω0. Jest amplituda n-tej harmonicznej dla pulsacji n*ω0, gdzie ω0 jest pulsacją funkcji okresowej f(t).
d. Wzór na an w funkcji okresu To. Jest to także amplituda n-tej harmonicznej dla okresu To/n, gdzie To jest okresem funkcji okresowej f(t). Z tego wzoru będziemy najczęściej korzystać. Przypominam, że ω0=2π/To.
Obliczmy np. a1(ω0=1π/sek)=a1(To=2sek). Czyli pierwszą harmoniczną dla fali prostokątnej z Rys. 3-2a.
Skorzystamy ze wzoru 3-5d
a1=(1/2)*sinc(1*π/2)=1/π≈0.318
Skorzystaliśmy z wykresu Rys. 3-5b, gdzie sinc(π/2)=2/π≈0.637
Uwagi
1. Wzory są ważne dla n=-∞…0…+∞. Dla n=0 harmoniczną jest składowa stała a0.
2. Pochodzą z całkowego wzoru Rys. 3-4d.
Dla niedowiarków- wyprowadzenie w rozdz. 3.5.7
Rozdz.3.5 Wykresy prążkowe dla funkcji okresowych
Ściślej dla funkcji okresowych a,b,c i d z Rys. 3-2.
Rozdz.3.5.1 Wstęp
Wywołaj jeszcze raz 4 animacje z Rys. 3-2.
Każda z nich jest:
– parzystą funkcją czasu f(t)
– falą prostokątną składającą z impulsów prostokątnych Tp=1sek powtarzającymi się co okres To.
– pierwszy impuls rozpoczyna się w czasie połowy jego trwania Tp=1sek i dlatego f(t) jest funkcją parzystą
Zbadamy wpływ zwiększającego się okresu To na wykres prążkowy. Skorzystamy ze wzoru Rys. 3-5d. Założono że A=1 i Tp=1sek. Dlatego jedynymi zmiennymi wzoru Rys. 3-5d są To jako okres pierwszej harmonicznej funkcji i n jako n-ta harmoniczna.
Rozdz.3.5.2 Wykres prążkowy dla fali A=1, Tp=1sek i T0=2sek
Dla pierwszej fali f(t), czyli dla Rys. 3-2a zrobiliśmy już wykres prążkowy w podrozdz. 2.4 rozdz. 2. Jest to typowa fala prostokątna o amplitudzie A=1 i okresie To=2sek. Jej współczynnik wypełnienia to 1/2. We wzorze Rys. 3-5d jedyną zmienną jest n, ponieważ okres fali jest stały To=2sek. Odpowiada on pulsacji ω0=1π/sek
Policzmy a(-n)=a(+n) dla n=0…3. wg wzoru Rys. 3-5d.
n=0–>ω=0*ω0=0
a(0)=(1/2)sinc*(0*π/2)=1/2=0.5 bo sinc(0)=1 wg. Rys. 3-5b
n=1–>ω=1*ω0=1π/sek
a(-1)=a(+1)=(1/2*)sinc(1*π/2)=1/(2π)≈0.318
n=2–>ω=2*ω0=2π/sek
a(-2)=a(+2)=(1/2)*sinc(2*π/2)=0
n=3–>ω=3*ω0=3π/sek
a(-3)=a(+3)=(1/2)*sinc(3*π/2)=-1/(3*2π)≈-0.106
Uwaga
Powyższe dane możesz sprawdzić programem WolframAlfa. A jak? Patrz Rozdział 11.2 Program WolframaAlfa artykułu “Wirujące Szeregi Fouriera” z górnej zakładki. Np. Aby obliczyć a(-3)=a(+3) wywołaj program WolframAlfa
Kliknij https://www.wolframalpha.com
Następnie wpisz lub wklej do okienka 0.5*sinc(3*pi/2)
i rób co każe obrazek.
Rys. 3-6
Program prawidłowo obliczył a(-3)=a(+3)=(1/2)sinc(3*π/2) -1/3π≈-0.106103.
Rys. 3-7
Wykres prążkowy fali prostokątnej A=1, Tp=1sek, To=2sek z Rys. 3-2a
Czyli stan harmonicznych przed animacją, czyli w stanie początkowym, czyli dla t=0. Co wynika z obrazka?
1. Niepulsująca składowa stała a0=0.5
2. Pulsacje pierwszej harmonicznej 1ω0=+1π/sek i -1ω0=-1π/sek
3. Są tylko nieparzyste harmoniczne +-1*π/sek, +-3*π/sek, +-5*π/sek…
4. Współczynniki a(+1), a(-1), a(+3), a(-3) są amplitudami +0.318, -0.106 pulsujących kresek.
Np. ujemne -0.106 oznacza, że taka była wartość 3 harmonicznej w stanie początkowym dla t=0.
5. Przedstawiono tylko 4 harmoniczne i składową a0=+0.5. Pozostałe tzn. dla ω=-∞…-5π/sek
i ω=+5π/sek…+∞ są niewidoczne.
6. Niewidoczne harmoniczne uwzględnione są jednak w pulsującej kresce f(t).Jest ona sumą wszystkich harmonicznych, niewidocznych też! Zauważ, że jest to idealna fala prostokątna. Bez “falek”, czyli efektu Gibbsa.
7. Fala prostokątna jako pulsująca kreska f(t) jest w fazie z pierwszą harmoniczną.
8. f(t)=…-(1/3π)*cos(3π*t)+(1/1π)*cos(1π*t)+0.5++(1/1π)*cos(1π*t)-(1/3π)*cos(3π*t)…
Animacja wykresu prążkowego i powyższe równanie przedstawiają dokładnie to samo. Funkcja f(t) jest pionową kreską pojawiającą się co To= 2sek, czyli z pulsacją 1ω0=+1π/sek. Harmoniczne z równania 8. widzisz jako pulsujące prążki z ω=-3π/sek, ω=-1π/sek, ω=0, ω=+1π/sek, ω=+3π/sek. Pozostałe harmoniczne są niewidoczne, ale uwzględnione w sumie na f(t). Dlatego widzisz prążek f(t) jako idealne skoki co To=2sek.
Rozdz.3.5.3 Wykres prążkowy dla fali A=1, Tp=1sek i T0=4sek
Czyli dla drugiej fali f(t) z Rys. 3-2b o wypełnieniu 3/4.
Rys. 3-8
Wykres prążkowy fali prostokątnej A=1, Tp=1sek, To=4sek–>ω0=π/2sek z Rys. 3-2b
Policzmy a(-n)=a(+n) dla n=0…6 wg. wzoru Rys. 3-5d.
n=0–>ω=0*ω0=0
a(0)=(1/4*)sinc(0*π/4)=(1/4)*1=1/4=0.25
n=1–>ω=1*ω0=1*π/2sek
a(-1)=a(+1)=(1/4)sinc(1*π/4)≈0.225
n=2–>ω=2*ω0=2*π/2sek=1*π/sek
a(-2)=a(+2)=(1/4)*sinc(2*π/4)≈0.159
n=3–>ω=3*ω0=3*π/2sek
a(-3)=a(+3)=(1/4)*sinc(3*π/4)≈0.159
n=4–>ω=4*ω0=4*π/2sek=2*π/sek
a(-4)=a(+4)=(1/4)*sinc(4*π/4)=0
n=5–>ω=5*ω0=5*π/2sek
a(-5)=a(+5)=(1/4)*sinc(5*π/4)≈-0.045
n=6–>ω=5*ω0=6*π/2sek=3*π/sek
a(-6)=a(+6)=(1/4)*sinc(6*π/4)≈-0.053
Wnioski
1. Składowa stała a0 i amplitudy harmonicznych są 2 razy mniejsze niż dla poprzedniej fali prostokątnej z Rys. 3-2b.
Zgadza się to z intuicją, gdyż impuls prostokątny jest 2 razy rzadszy.
2. Obwiednia pulsujących prążków też jest 2 razy mniejsza w pionie. Wynika to ze wzoru Rys. 3-5d. Oznacza to, że punkty zerowe ω=1π, 2π, 3π…są takie same. Dotyczy to oczywiście wszystkich fal prostokątnych z Rys. 3-2.
3. Prążki są 2 razy gęściej rozmieszczone. To też wynika ze wzoru Rys. 3-5d, ale spróbuję podeprzeć intuicją. Trudniej chyba dobrać cosinusoidy, aby zsumowały się w impuls który pojawia się rzadziej! Robota musi być bardziej subtelna. Tzn. harmoniczne są nie tylko 2 razy mniejsze ale jest ich 2 razy więcej. Tak jak z większej liczby klocków Lego, ale mniejszych i bardziej skomplikowanych, można zbudować bardziej skomplikowany samochodzik. Ten rzadszy impuls, to taki bardziej skomplikowany samochodzik.
4. Zwróć uwagę na rzadziej pojawiający się impuls A=1 Tp=1sek.
Rozdz.3.5.4 Wykres prążkowy dla fali A=1, Tp=1sek i T0=8sek
Czyli dla trzeciej fali f(t) z Rys. 3-2c o wypełnieniu 7/8.
Rys. 3-9
Wykres prążkowy fali prostokątnej A=1, Tp=1sek, To=8sek–>ω0=π/4sek z Rys. 3-2c
Policzmy a(-n)=a(+n) dla n=0…12 wg. wzoru Rys. 3-5d.
n=0–>ω=0*ω0=0
a(0)=(1/8)*sinc(0*π/8)=1/8=0.125
.
.
n=12–>ω=12*ω0=3*π
a(12)=(1/8)*sinc(12*π/8)≈-0.026
Podałem tylko 2 obliczenia resztę możesz sobie obliczyć WolframemAlfa
Impuls f(t) pojawia się co To=8 sek.
Rozdz.3.5.5 Wykres prążkowy dla fali A=1, Tp=1sek i T0=16sek
Czyli dla czwartej fali f(t) z Rys. 3-2d o wypełnieniu 15/16.
Rys. 3-10
Wykres prążkowy fali prostokątnej A=1, Tp=1sek, To=16sek–>ω0=π/8sek z Rys. 3-2d
Policzmy a(-n)=a(+n) dla n=0…24 wg. wzoru Rys. 3-5d.
n=0–>ω=0*ω0=0
a(0)=(1/16)* sinc(0*π/16)=1/16=0.0625
…
…
n=24–>ω=24*ω0=3*π
a(24)=(1/16)*sinc(24*π/16)≈-0.013
Impuls f(t) pojawia się co To=16 sek
Jeszcze raz podkreślam.
Wykres prążkowy, a zwłaszcza jego animacja, jest najbardziej intuicyjnym przedstawieniem Szeregu Fouriera. Widać to, czego nie widać we wzorze Rys. 3-4. Tj. wzajemnej korelacji między kolejnymi harmonicznymi jak np. na Rys. 3-10. A animacja to już jest kosmos! Widać f(t)-lewą stronę Szeregu Fouriera jako sumę bujających się prążków-harmonicznych. Funkcja f(t) jest impulsem A=1 Tp=1sek pojawiającym się co To=16sek.
Rozdz.3.5.6 Wpływ zwiększającego się okresu To na wykres prążkowy?
Na Rys. 3-2 impuls ma stałą amplitudę A=1 i czas trwania Tp=1sek. Zwiększa się natomiast okres To fali prostokątnej. Impuls staje się coraz bardziej samotny, stopniowo upodobniając się do pojedynczego impulsu. Na zwykłych, czytaj statycznych wykresach prążkowych, tego nie widać, ale na animacjach jak najbardziej.
Wróćmy do wniosków, czyli co się dzieje prążkami gdy okres To rośnie? Przypominam, że n-ty prążek jest n-tą harmoniczną. Widzisz tylko najważniejsze początkowe prążki w zakresie ω=-3π/sek…0…+3π/sek. Pozostałe niewidoczne i dążące do zera musisz sobie wyobrazić.
Najważniejsze wnioski.
1. Są coraz gęściej położone
2. Obwiednia prążków spłaszcza się.
3. Miejsca zerowe ω=…-3π,-2π,-1π,0,+1π,+2π,+3π…są stałe.
4. Maksyma 1/2,1/4,1/8,1/16 odpowiadają prążkom zerowym,
czyli składowym stałym a(0) Szeregów Fouriera fal prostokątnych z Rys. 3-2a,b,c,d.
5. Suma wszystkich prążków-harmonicznych jest funkcją f(t) i pojawia się co okres 2,4,8 lub 16sek jako pionowa kreska-idealna fala prostokątna.
Rozdz.3.5.7 Wyprowadzenie wzoru dla chętnych
Rys. 3-11
Wyprowadzenie wzoru na Szereg Fouriera dla fali z Rys. 3-1b
Jest to funkcja f(t) mocno wyspecjalizowana i dotyczy tylko ciągu impulsów o amplitudzie A=1 i czasie trwania Tp=1sek. Zmienia się tylko okres funkcji To albo pulsacja ωo. Pulsacja ωo dotyczy pierwszej harmonicznej i jest także odstępem Δω=ω0 między prążkami. Wystarczy elementarna znajomość rachunku całkowego. Wzór jest ważny także dla składowej stałej–> n=0.
