Transformata Fouriera
Rozdz. 2 Szereg Fouriera fali prostokątnej jako wykres prążkowy
Rozdz. 2.1 Wykres czasowy fali prostokątnej
W następnym rozdziale zbudujemy Transformatę Fouriera najprostszej funkcji nieokresowej jaką jest pojedynczy impuls prostokątny. Wiąże się on w jakiś sposób z falą prostokątną parzystą którą rozłożyliśmy na Szereg Fouriera w artykule “Wirujące Szeregi Fouriera” rozdz.8. W opisie często pojawia się pojęcie tzw. wykresu prążkowego, który jest po prostu Szeregiem Fouriera w wersji graficznej. W tym rozdziale pokażemy kilka wykresów prążkowych dla przybliżenia fali prostokątnej o różnych okresach, jako sumy S7(t) kilku jej pierwszych harmonicznych.
Rys. 2-1
Fala prostokątna o parametrach:
A=1-amplltuda
ω0=1/sek-pulsacja odpowiadająca okresowi T=2πsek≈6.28sek.
ϕ=0
50%-wypełnienie
Przebieg rozpoczął się teoretycznie na początku świata dla t=-∞ w połowie impulsu gdy A=1.
Czyli dla t=0 też będzie w połowie impulsu. Jest to więc funkcja parzysta. Podobnie jak np. cosinus, który też rozpoczyna się w “środku”. Lewej półosi czasu t nie pokazano.
Rozdz. 2.2 Siódme przybliżenie fali prostokątnej parzystej czyli S7(t)=c0+h1(t)+h3(t)+h5(t)+h7(t).
W rozdz.8 artykułu “Wirujące Szeregi Fouriera” obliczyliśmy przybliżenie fali prostokątnej parzystej S7(t) gdy ω0=1/sek—>Rys. 2-3
Współczynniki an przy cos(nω0t) obliczyliśmy jako podwojone środki ciężkości scn trajektorii F(njω0t) funkcji f(t)=fala prostokątna parzysta. Jeżeli nie za bardzo kojarzysz o co chodzi z tymi środkami ciężkości, to po prostu obliczyliśmy współczynniki a(n) Szeregu Fouriera. Pozostałych harmonicznych tzn. dla n>7 nie uwzględniliśmy, co objawiło się “falistym” przybliżeniem s7(t) fali prostokątnej.
Parzyste harmoniczne hn(t) są zerowe, bo a(2)=a(4)=a(6)=…0. Dla n=∞ otrzymalibyśmy idealną falę prostokątną z animacji Rys. 2-1.
Wszystkie współczynniki Szeregu Fouriera b(n) są zerowe, bo f(t) jest funkcją parzystą.
Rys.2-2
S7(t)=c0+h1(t)+h3(t)+h5(t)+h7(t)
Na animacji widzisz
– falę prostokątną parzystą o okresie T=2π, czyli ω=1/sek
– jej siódme przybliżenie S7(t) jako niecałkowity Szereg Fouriera.
– składową stałą c0=a0=0.5
– harmoniczne h1(t), h3(t), h5(t) i h7(t).
Po podstawieniu konkretnych parametrów ω0, a(1), a(3),a(5) i a(7) z opisu powyżej otrzymamy wzór na S7(t) jako przybliżenie Szeregiem Fouriera funkcji f(t) .
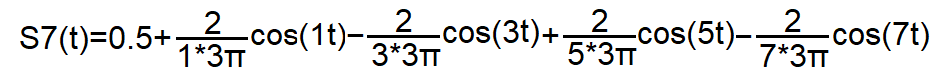
Rys.2-3
Konkretny wzór na przybliżenie Szeregu Fouriera fali prostokątnej z Rys. 2-1
Rozdz. 2.3 Jednowstęgowy prążkowy wykres fali prostokątnej
Jednowstęgowy, bo tylko dla pulsacji nieujemnych.
Najdokładniejszą wersją Szeregu Fouriera jest oczywiście sam jego wzór. Dla np. n=7 i dla fali prostokątnej parzystej jest to Rys. 2-3.
Mniej dokładną (bo zależną od wieku i okularów obserwatora), ale bardziej intuicyjną wersją są wykresy czasowe np. Rys. 2-2. Widoczna jest sama funkcja prostokątna, składowa stała i 4 harmoniczne przybliżenia S7(t). Widzimy jak składowe się sumują dając S7(t).
Wykres prążkowy jako animacja, jest najbardziej intuicyjny. Dokładnie są widoczne pulsacje ω i amplitudy a(n) harmonicznych i składowa stała a0. A gdzie faza φ? Nigdzie. Bo wykres prążkowy nadaje się tylko do analizy funkcji parzystych f(t). Funkcje te mają tylko składową rzeczywistą, w których zawsze φ=0 albo φ=180º!
Zróbmy więc prążkowy wykres dla S7(t) z Rys. 2-3. Czyli dla przybliżenia fali prostokątnej z Rys. 2-1 gdy n=7.
Rys. 2-4
Jednowstęgowy wykres prążkowy fali prostokątnej dla n=7
Ściślej jest to animacja wzoru z Rys. 2-3, a wykres prążkowy który widzisz na Rys. 2-4 jest stanem początkowym S7(t), czyli dla t=0. Harmoniczne hn(t) dla pulsacji ω parzystych są zerowe. Inaczej – nie istnieją.
1. Animacja trwa ok 3T=3*2π sek≈19sek
2. Na poziomej osi ω umieszczono pulsacje harmonicznych dla ω=0…+7/sek.
3. a0=+0.5 składowa stała fali prostokątnej czyli prążek dla ω=0
4. Animacja pierwszej harmonicznej h1(t) czyli prążek dla ω=1/sek
…
7. Animacja siódmej harmonicznej h7(t) czyli prążek dla ω=7/sek
8. Suma S7(t) a0 i 4 harmonicznych hn(t) czyli lewy krańcowy prążek. Porównaj z S7(t) na Rys. 2-2. Zauważ, że jest w fazie z h1(t). Gdyby n=∝ to widziałbyś idealne “prostokątne” ruchy bez drgań, takie jak na Rys. 2-1. Bez tzw. efektu Gibbsa-maksymalnej “bujawki” na początku i końcu impulsu.
W stanie początkowym t=0 widzisz amplitudy harmonicznych hn(t), czyli ze współczynnikami Fouriera a(n) fali prostokątnej z Rys. 2-2. Ujemne amplitudy dla h3(t) i h7(t) oznaczają, że takie są wartości w chwili początkowe dla t=0, co wynika ze wzoru Rys. 2-3. Innymi słowy φ=-180º, bo w tej fazie “startują” cosinusoidy h3(t), h7(t), … gdy t=0. Funkcja f(t)=S(t) z lewej strony wykresu, jest w każdej chwili sumą bujających się wszystkich prążków, czyli składowej stałej a0 i 4 harmonicznych h1(t), h3(t), h5(t) i h7(t). “Bujają” się z pulsacjami ω=n*ω0=n*1/sek czyli z ω=1/sek, 3/sek, 5/sek i 7/sek. Linia kropkowana jest składową stałą a0=0.5. Podkreślam, że animacja z bujającymi się prążkami, jest najbardziej intuicyjną wersją Szeregu Fouriera! Widzisz sumę S7(t), 4 harmoniczne hn(t) i składową stałą a0. A same współczynniki Fouriera są prążkami w chwili początkowej. Składową stałą a0 możemy traktować formalnie jako harmoniczną h0(t) o pulsacji zerowej.
Uwaga:
Skoro wykres prążkowy jest taki fajny i intuicyjny, to dlaczego nie jest stosowany dla wszystkich funkcji okresowych f(t)? Odpowiedź jest prosta. Bo dotyczy tylko funkcji funkcji parzystych, dla których Szereg Fouriera nie ma składowych sinusoidalnych, czyli bn.
Rozdz. 2.4 Dwuwstęgowy prążkowy wykres fali prostokątnej
Lewa “ujemna” półoś ω na Rys. 2-4 jest, oprócz prążka f(t), niezagospodarowana. Co za marnotrawstwo!
Z trygonometrii wiadomo, że cos(ωt)=cos(-ωt). Podzielmy więc każdą harmoniczna hn(t) przez 2 i obdzielmy nimi 2 półosie ω.
Czyli h+n(t)=h-n(t)=hn(t)/2
Stworzyliśmy więc dwuwstęgowy prążkowy wykres fali prostokątnej.
Rys. 2-5
Dwuwstęgowy wykres prążkowy fali prostokątnej dla n=7
Każdy prawy prążek h+n(t) harmonicznej ma swój symetryczny lewy odpowiednik h-n(t).
Z oczywistych powodów
1. a0=+0.5 składowa stała fali prostokątnej czyli prążek dla ω=0 i jest taki sam jak a0 dla dwuwstęgowego na Rys. 2-4
2. Pozostałe harmoniczne, czyli “bujawki” są połówkami z Rys. 2-4
3. f(t) jest takie same jak na Rys. 2-4
Po co to wszystko? Okaże się, że wprowadzenie ujemnych pulsacji spowoduje pewną elegancję we wzorach. Nawet animacja jest bardziej estetyczna niż Rys. 2-4.
Pamiętasz środki ciężkości scn trajektorii F(njω0t) w artykule “Wirujące Szeregi Fouriera?”. Intrygowało mnie dlaczego cn=2*scn. Dlaczego zespolona amplituda n-tej harmonicznej hn(t), czyli cn jest podwojonym scn, a nie po prostu (pojedynczym) scn. Tako rzecze matematyka. Zgoda, ale z tyłu głowy dręczyło “dlaczego?”. Teraz wiem. Bo harmonicznymi trzeba obdzielić dodatnie i ujemne pulsacje!
Rozdz. 2.5 Wpływ pulsacji fali prostokątnej na wykresy prążkowe.
Rozdz. 2.5.1 Wstęp
Ściślej, Wpływ na wykresy prążkowe dwuwstęgowe, bo tylko takimi będziemy interesować. Rys. 2-5 jest wykresem prążkowym fali prostokątnej parzystej z Rys. 2-1 o okresie T=2π sek–>ω=1/sek. Gdyby amplituda była A=2 to wykres byłby 2 razy wyższy. Jest to oczywiste. A okres T?
Zbadamy 2 przypadki, bo pierwszy-T=2π sek–>ω=1/sek to jw. Rys. 2-5.
– T=4π sek–>ω=0.5/sek
– T=1π sek–>ω=2/sek
Rozdz. 2.5.2 Wykres prążkowy fali prostokątnej o okresie T=4π sek–>ω=0.5/sek
Rys. 2-6
Fala prostokątna o parametrach:
A=1-amplltuda
ω0=0.5/sek-pulsacja odpowiadająca okresowi T=4π sek.
ϕ=0
50%-wypełnienie
Fala podobna tej z Rys. 2-1. Tylko mniejsza pulsacja ω0=0.5/sek czyli T=4π sek. Ciekawe jak wpłynie to na wykres prążkowy.
Uwaga
Animacja jest myląca nieco. Wygląda tak jakby w okresie T=4πsek były 2 impulsy prostokątne o czasie trwania Tp=1π sek. A jest to 1 impuls prostokątny o czasie Tp=2π sek, “startujący” w czasie t=0 sek w połowie impulsu. Potem te impulsy łączą się w jeden impuls Tp=2π sek powtarzający się co T=4π sek. Problem “mylącej animacji” z oczywistych powodów nie wystąpi na Rys. 2-8 dla T=1 1π sek.
Rys. 2-7
Dwuwstęgowy wykres prążkowy fali prostokątnej z Rys. 2-6 dla n=7
Prążki są 2 razy wolniejsze i 2 razy “gęstsze” niż na Rys. 2-5.
Rozdz. 2.5.3 Wykres prążkowy fali prostokątnej o okresie T=1π sek–>ω=2/sek
Rys. 2-8
Fala prostokątna o parametrach:
A=1-amplltuda
ω0=2/sek-pulsacja odpowiadająca okresowi T=1π sek.
ϕ=0
50%-wypełnienie
Fala podobna tej z Rys. 2-1. Tylko większa pulsacja ω0=2/sek czyli T=1π sek.
Rys. 2-9
Dwuwstęgowy wykres prążkowy fali prostokątnej z Rys. 2-8 dla n=7
Prążki są 2 razy szybsze i 2 razy “rzadsze” niż na Rys. 2-5.
Rozdz. 2.6 Wnioski
1. Większy sygnał–>Wyższe prążki
2. “Szerszy w czasie sygnał”—>Gęściej rozłożone prążki
Wybiegając w przyszłość i uogólniając na Transformatę Fouriera
1. Większy sygnał–>Wyższa transformata
2. “Szerszy w czasie sygnał”—>Węższa Transformata
