Scilab
Rozdział 8 ODE- Funkcja do rozwiązywania równań różniczkowych zwyczajnych ODE
Rozdział 8.1 Wstęp
Ten rozdział dotyczy bardziej matematyki niż Scilaba. Jeśli nie wszystko jest jasne, możesz go pominąć.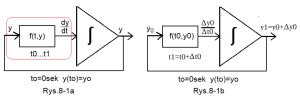
Rys.8-1
Jak układ całkujący rozwiązuje równanie różniczkowe I rzędu y'(t)=f(t,y)?
Układ z członem całkującym rozwiązuje równanie różniczkowe y'(t)=f(t,y), dla warunków początkowych y(to)=yo. Innymi słowy, całe równanie różniczkowe jest “zaklęte” w czerwonym obramowaniu na Rys.8-1a. Uwaga dotyczyć będzie także dalszych analogicznych schematów z układami całkującymi. Niby z samego układu wynika, że tu w każdej chwili t ewidentnie jest y'(t)=f(t,y). Zwłaszcza, że na wyjściu każdego układu całkującego jest y(t),a na wejściu pochodna y'(t). Ale gdzie tu jest początek i koniec zdarzeń? Wąż jedzący własny ogon! Ot takie sobie wątpliwości. Powinny zniknąć przy analizie Rys.8-1b. Tu przynajmniej widać co jest początkiem. Mianowicie stan początkowy y(t0)=yo. Czyli dla to=0sek na wyjściu układu całkującego jest napięcie yo. Najczęściej zresztą yo=0. Z Rys.8-1b wynika, że dla stanu początkowego (to,yo) można obliczyć iloraz różnicowy Δy0/Δto≈f(t0,yo), czyli y1=y0+Δy0. I co dalej? Znowu obliczymy nowe Δy1/Δt1≈f(t1,y1), czyli y2=y1+Δy1. Itd. Tak otrzymamy ciąg przebiegu wyjściowego y0,y1,y2…yn. Jest to przybliżone rozwiązanie równania różniczkowego dy/dt=f(t0,yo) przy warunkach początkowych y(to)=yo.
Wniosek:
Układ analogowy z lat 50 jest protoplastą funkcji ODE-podstawowego narzędzia do rozwiązywania równań różniczkowych zwyczajnych I rzędu. A później jak się okaże, także dowolnego rzędu.
Rozdział 8.2 Rozwiązanie y'(t)=1-y(t) równania przy pomocy ODE
ODE-czyli funkcja rozwiązująca dowolne równanie różniczkowe zwyczajne I rzędu
y'(t)=f(t,y)
przy warunkach początkowych
y(to)=y(o)
Jest to realizacja numeryczna układu całkującym z Rys. 8-1 dla dowolnej funkcji f(t,y) z warunkami początkowymi y(to)=f(to).
Numeryczne rozwiązanie dla konkretnej funkcji f(t,y)=1(t)-y(t) podano w Rozdz. 7 na Rys.7-7 i realizuje to program 7-2.
W podobny sposób, tylko dla dowolnego f(t,y), działa funkcja ODE.
Sprawdźmy działanie ODE dla f(t,y)=1(t)-y(t) w poniższym programie
Program P8-1 z funkcją ODE bez komentarzy
clc;
clear;
clf();
function ydash=f(t, y)
ydash=1-y
endfunction
t=[0:0.1:10]
t0=0
y0=0
y=ode(y0,t0,t,f)
plot(t,y,'--or')Ten sam program z komentarzami. Przeanalizuj go
clc;//czyszczenie konsolki
clear;//czyszczenie zmiennych
clf();//czyszczenie wykresu
function ydash=f(t, y)//Tu zaczyna się funkcja ode jako ogólne równanie różniczkowe y'=f(t,y)
ydash=1-y//Tu jest konkretne równanie różniczkowe do rozwiązanie przez ODE
endfunction//Tu kończy się funkcja ode
t=[0:0.1:10]//zakres czasowy funkcji ode czyli t od 0 do 10 z odstępem Δ=0.1
t0=0//czas początkowy ode
y0=0//stan początkowy y dla to=0
y=ode(y0,t0,t,f)// ODE na podstawie stanu początkowego yo,to dla każdego tn oblicza yn.
plot(t,y,'--or')//rysuje wykres y=f(t)Uwaga:
y’ to inaczej ydash–>dash, apostrof ‘, symbol pochodnej.
Wykonaj program P8-1. Pomocna będzie poniższa animacja.
Rys.8-2
Jak wykonać program P8-1?
Widzisz końcowy efekt animacji z obliczonym wykresem y(t), który jest rozwiązaniem równania różniczkowego y'(t)=1-y(t)
1. Ustaw obok siebie okna kursu Scilaba i Konsoli Scilaba.
2. Wywołaj edytor Scinotes (tu pominąłeś ostatni plik edycji)
3. Skopiuj program P8-1 z kursu Scilaba
4. Wpisz P8-1 do edytora Scinotes
5. Wykonaj bez echa. Tu Scilab każe go gdzieś zapisać.
6. Zapisz w dowolnym miejscu, pod dowolną nazwą program P8-1.
7. Został wykonany wykres y(t) jako rozwiązanie równania y'(t)=1-y(t) przy warunkach początkowych y(0)=0.
Efektem jest wykres na Rys. 8-2 którego “kólka” odpowiadają odstępom Δ=0.1sek z instrukcji t=[0:0.1:1].
Proponuje samodzielnie wykonać program P8-1. Zmień tylko instrukcję plot(t,y,’–or’) na plot(t,y,’r’). Wtedy wykres będzie ciągły.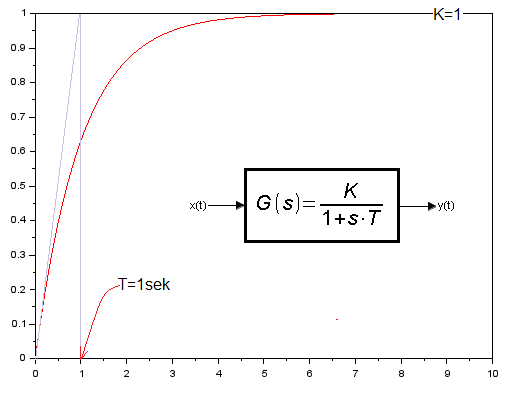
Rys. 8-3
Rozwiązanie równania różniczkowego y'(t)=1-y(t) jako wykres y(t).
W następnym rozdziale dowiesz się, że y(t) jest to odpowiedzią członu inercyjnego K=1 i T=1sek na skok jednostkowy.
Rozdział 8.3 Rozwiązanie równania różniczkowego y'(t)=1.5-2y*(t) przy pomocy ODE
Okrętem flagowym portalu są Podstawy Automatyki,w którym wszystkie doświadczenia zostały wykonane w Scilabie, a ściślej w w jego aplikacji XCOS. Inna rzecz, że czytelnik nie ma tu do czynienia ze Scilabem. A kto ma? Autor kursu który dla wygody czytelników nagrał animacje ćwiczeń wykonanych Scilabem programem ActivePresenter. Wróćmy do Podstaw Automatyki. Na początku kursu poznajesz tzw. człony dynamiczne. Proporcjonalny, Inercyjny, Oscylacyjny… itd. Ich dynamikę opisuje tzw. transmitancja G(s). Poniżej pokazano człon inercyjny.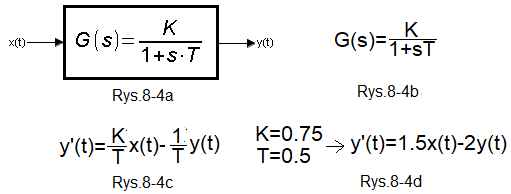
Rys. 8-4
Badanie członu inercyjnego funkcją ODE
Rys. 8-4a
Człon inercyjny
Rys. 8-4b
Transmitancja G(s) członu inercyjnego
K wzmocnienie
T stała czasowa
Rys. 8-4c
Równanie różniczkowe opisujące transmitancję członu inercyjnego.
Uwaga:
Związek między transmitancją G(s) a równaniem różniczkowym pokazano w kursie Podstawy Automatyki Rozdz. 15.3
Rys. 8-4d
Równanie różniczkowe członu inercyjnego dla K=0.75 i T=0.5sek. Gdy sygnałem wejściowym x(t) jest skok jednostkowy 1(t), to otrzymamy równanie z tytułu rozdziału, tj. y'(t)=1.5-2y*(t).
Zbadajmy ten człon Scilabem przy pomocy funkcji ODE Interpretacja z wykresu parametrów wzmocnienia K i stałej czasowej T jest oczywista.
Program P8-2 z funkcją ODE
clc;
clear;
clf();
function ydash=f1(t, y)
ydash=1.5-2*y
endfunction
t=[0:0.1:10]
t0=0
y0=0
y=ode(y0,t0,t,f1)
plot(t,y,)
t0=0
y0=0
y=1
plot(t,y,)Opis programu P8-2 z funkcją ODE
Czym różni się od P8-1?
1. instrukcja ydash=1.5-2*y zamiast ydash=1-y
2. instrukcja plot(t,y,) zamiast plot(t,y,’–or’) –>wykres ciągły niebieski.
3. dodatkowy ciąg instrukcji, który wykreśla funkcję y=1. Dzięki temu wykresy z Rys. 8-5 i Rys. 8-3 mają te same skale.
t0=0 y0=0 y=1 plot(t,y,)
Wykonaj program P8-3. Otrzymasz wykres na Rys. 8-5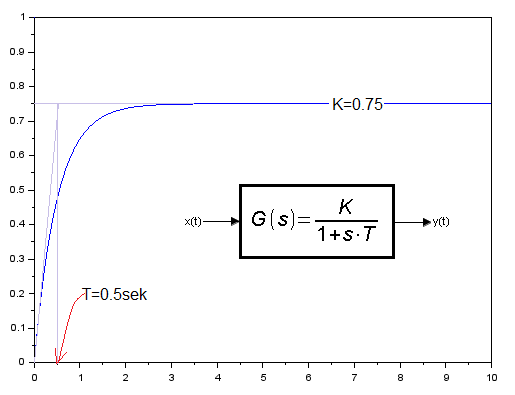
Rys. 8-5
Rozwiązanie równania różniczkowego y'(t)=1.5-2*y(t) jako wykres y(t).
W nawiązaniu do Rys. 8-4 jest to odpowiedź członu inercyjnego o parametrach K=0.75 i T=0.5 sek na skok jednostkowy.
Interpretacja parametrów K i T jest oczywista. Spójrz jeszcze raz na Rys.8- 3 z członem inercyjnym K=1 i T=1sek.
Rozdział 8.4 Rozwiązanie równania różniczkowego y”(t)=0.5-0.125*y'(t)-0.25*y(t) przy pomocy ODE
Rozdział 8.4.1 Ogólnie o powyższym równaniu i jego związku z członem oscylacyjnym.
Jak się okaże mamy tu do czynienia z odpowiedzią na skok jednostkowy członu oscylacyjnego o parametrach K=2, T=2sek i q=0.5.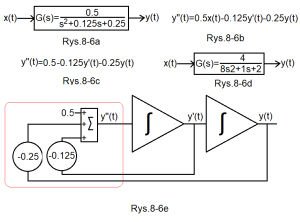
Rys.8-6
Człon oscylacyjny i jego równanie różniczkowe
Rys.8-6a
Transmitancja G(s) tego członu
Na pierwszy rzut oka nie widać, że G(s) jest członem oscylacyjnym. A może to 2-inercyjny?
Rys.8-6b
Równanie różniczkowe bezpośrednio związane z G(s) z Rys.8-6a.
Nawet jeżeli nie wiesz, co to jest transmitancja, spróbuj znaleźć zależność od G(s).
Rys.8-6c.
Równanie różniczkowe gdy x(t) jest tzw. skokiem jednostkowym czyli x(t)=1(t). Czyli 0.5x(t)=0.5*1(t)=0.5.
Ponieważ 1(t)=0 dla t<0 i 1 dla t>1, a zakres równania dotyczy t>0.
Rys.8-6d
Dokładnie ta sama transmitancja jak Rys.8-6a, tylko inaczej napisana.
Ale z niej można otrzymać parametry członu oscylacyjnego K=2, T=2sek q=0.25.
Patrz kurs Podstawy Automatyki rozdz. 7 Rys. 7-3.
Rys.8-6e
Układ z 2 członami całkującymi opisujący równanie z Rys.8-6c
Zauważ, że rozwiązuje on równanie y”(t)=0.5-0.125y(t)-0.25y(t), analogicznie jak układ z jednym członem całkującym
z Rys. 7-6 rozdz. 7 rozwiązuje równanie y'(t)=1(t)-y(t). Równanie różniczkowe drugiego stopnia też jest zawarte w czerwonym obramowaniu, tak jak na Rys.8-1a.
Rozdział 8.4.2 Jak ODE rozwiązuje równanie y”(t)=0.5-0.125*y(t)-0.25*y(t)?
Nie będę przeprowadzał dokładnej analizy jak w sposób przybliżony rozwiązać równanie różniczkowe zwyczajne 2 stopna y”=x(t)-a*y'(t)-b*y(t). Albo bardziej ogólnie y”(t)=f[t,y'(t),y(t)] .
Dla równania I stopnia y'(t)=f[t,y(t)] zastąpiliśmy je przybliżonym równaniem różnicowym Δy/Δt=f[t,y(t)] przy warunkach początkowych y(to)=yo a wtedy:
Δyo/Δt=f(to,yo) –>Δyo=f(to,yo)Δt
Czyli obliczymy y1=y0+Δyo=y0+f(to,yo)Δt
Analogicznie znając y1 obliczymy y2 (bo obliczymy Δy1/Δt1=f(t1,y1) itd…
Czyli
y2=y1+f(t1,y1)Δt
y3=y2+f(t2,y2)Δt
y4=y3+f(t3,y3)Δt
Zakładamy, że przyrosty czasu Δt są równe–>Δt0=Δt2=Δt3=Δt4=…=Δt.
Zauważ, że na podstawie poprzedniego stanu y(n) obliczymy następny stan y(n+1). Jest to tzw. równanie rekurencyjne Stan pierwszy, początkowy znamy y(0)=yo.
Podobnie będzie z równaniem 2 stopnia. Ale tu mamy 2 stany początkowe, funkcję y(to) i jej pochodną y'(to). Tu pierwszą pochodną też zastąpimy ilorazem różnicowym Δyo/Δt=f(to,yo) a drugą pochodną (“pochodną z pochodnej”), ilorazem różnicowym (“przyrostem z przyrostu”) Δ(Δy/Δt)/Δt. Nie wnikając w szczegóły doprowadzi nas to do “podwójnego” równania rekurencyjnego y(n+2)=f[y(n+1)] oraz y(n+1)=f[y(n)]. Czyli mając 2 warunki początkowe y(to) i y'(to) obliczymy wszystkie y(2),y(3),y(4)…y(n),y(n+1). Zaraz, zaraz. A gdzie y(0),y(1)? To łatwo obliczymy z wartości początkowych y(to)=yo i y'(to)=y'(o). Suma summarum w sposób przybliżony rozwiążemy równanie różniczkowe 2 rzędu.
Czytelniku drogi, może jest to zbyt ogólnikowe i nie skumałeś wszystkiego. Nie przejmuj się. Jest to zadanie dla funkcji ODE. Ty tylko musisz wprowadzić do niej odpowiednie parametry. Ale najważniejsze jest to, że jedno równanie drugiego rzędu zastąpimy dwoma równaniami pierwszego rzędu.
Rozdział 8.4.3 Jak ODE traktuje równanie y”(t)=0.5-0.125*y(t)-0.25*y(t)?
Przede wszystkim zamienia jedno równanie różniczkowe drugiego stopnia na dwa równania pierwszego stopnia. Jak? A tak jak poniżej.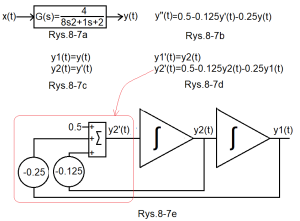
Rys.8-7
Człon oscylacyjny i jego równanie różniczkowe jako dwa równania pierwszego stopnia
Rys.8-7a
Człon oscylacyjny
Czyli Rys.8-6d równoważny Rys.8-6a
Rys.8-7b
Równanie różniczkowe opisujące człon oscylacyjny
Rys.8-7c
Podmianka
Rys.8-7d
Wersja dwóch równań pierwszego stopnia zamiast jednego równania drugiego stopnia z Rys.8-7b
Rys.8-7e
Układ analogowy z dwoma układami całkującymi rozwiązujący układ różniczkowych z Rys.8-7d
Dodam od siebie, że da taką samą odpowiedź jak układ z Rys.8-6e, co jest chyba oczywiste.
Wniosek:
Jedno równanie różniczkowe drugiego stopnia można zamienić na układ dwóch równań różniczkowych pierwszego stopnia
Wniosek ogólny:
Jedno równanie różniczkowe trzeciego stopnia można zamienić na układ trzech równań różniczkowych pierwszego stopnia.
itd…
A jak się ma do tego ODE?
A tak!
Program P8-3
clc;
clear;
clf();
function ydash=f(t, y)
ydash=[y(2);0.5-0.125*y(2)-0.25*y(1)]//za symbolem ";" wpisaliśmy prawą stronę równania y2'(t)=... z Rys.8-7d
endfunction
t=[0:0.1:100]//zakres 0<=t<=100 z odstępami Δt=0.1
t0=0//warunki początkowe t0=0sek
y0=[0;0]///warunki początkowe y2(0)=0 i y1(0)=0 czyli y(0)= i y'(0)=0
y=ode(y0,t0,t,f)//wywołanie funkcji ODE
plot(t,y(1,:))
xgrid(1,1,3)Opis programu P8-3
ydash=[y(2);0.5-0.125y(2)-0.25*y(1)]
Jest to zapis jednego równania różniczkowego drugiego stopnia z jedną niewiadomą y(t) z Rys.8-7b w wersji dwóch równań stopnia pierwszego z Rys.8-7d.
Uwaga:
W programie P8-1 było ydash=1-y. A tu pojawiają się jakieś symbole nawiasów kwadratowych? Bo dotyczą dwóch zmiennych y2(t) i y1(t) z Rys.8-7c. Zapisanych jako y1′(t) i y2′(t) z Rys, 8-7d. Czyli wektor [y1′(t),y2′(t)] czyli wektor [y(2);0.5-0.125y(2)-0.25*y(1)]. Tu y2(t) zaznaczyliśmy symbolem y(2) a y1(t) symbolem y(1). Nie kojarzyć z jakąś rekurencją!!!
Skopiuj i wykonaj ten program w aplikacji Scinotes podobnie jak w animacji Rys.8-2
Otrzymasz taki wykres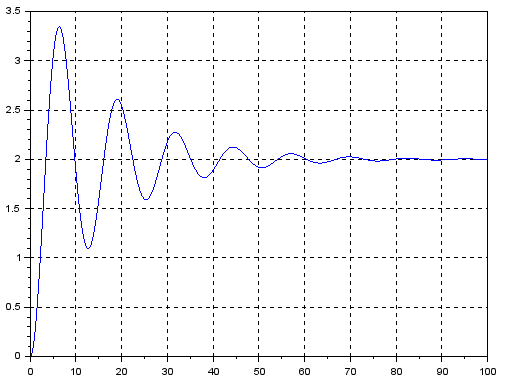
Rys. 8-8
Wykres y(t) jako rozwiązanie równania Rys.8-7b przy warunkach początkowych y(0)=0 i y'(0)
Tu może pojawić się wątpliwość co do pochodnej na Rys. 8-8. y'(0)≠0–>nie jest zerowa! ! Tak, ale powinno być y'(0)=0 z dopiskiem- dla równania jednorodnego, czyli dla y'(t)=-0.125y'(t)-0.25y(t). A nie takim z 0.5 jak na Rys.8-7b.
Uwaga:
Więcej o tym członie oscylacyjnym przeczytasz w kursie “Podstawy Automatyki” Rozdz. 7.
Rozdział 8.5 Rozwiązanie nieliniowego równania różniczkowego y”(t)=0.5-0.125*y'(t)-0.25*√y(t) przy pomocy ODE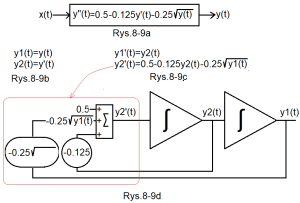
Rys.8-9
Człon oscylacyjny nieliniowy
Dlaczego nieliniowy? Bo zamiast 0.25*y (jak na Rys. 8-7b) jest na Rys. 8-9a 0.25*√y (0.25*pierwiastek z y”)
Rys.8-9a
Ze względu na nieliniowość, człon dynamiczny nie może być opisany jako transmitancja G(s) tak na Rys. 8-7a. Za to jego dynamika bardziej ogólnie jako równanie różniczkowe.
Rys.8-9b
Podmianka analogiczna do Rys.8-7c. Nieliniowość nie ma znaczenia.
Rys.8-9c
Podobnie jak Rys.8-7d
Rys.8-9d
Podobnie jak Rys.8-7e. Różnica tylko w elemencie pierwiastkującym. Całość rozwiązuje równanie różniczkowe z tytułu rozdziału.
Wersją cyfrową Rys.8-9d jest poniższy program P8-4 z funkcją ODE. Komentarze są tu chyba zbyteczne. Jedyna różnica to funkcja pierwiastkująca sqrt(y(1)) użyta w ODE
Program P8-4
clc;
clear;
clf();
function ydash=f(t, y)
ydash=[y(2);0.5-0.125*y(2)-0.25*sqrt(y(1))]
endfunction
t=[0:0.1:100]
t0=0
y0=[0;0]
y=ode(y0,t0,t,f)
plot(t,y(1,:))
xgrid(1,1,3)Skopiuj i wykonaj go podobnie jak program P8-4. 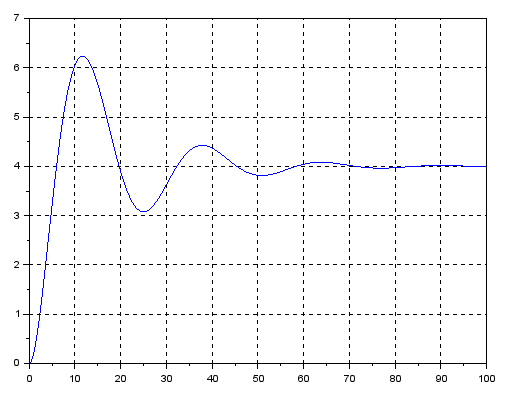
Rys. 8-10
Rozwiązanie równania różniczkowego nieliniowego
W porównaniu do Rys.8-8 odpowiedź jest bardziej wytłumiona i leniwa. Taki jest efekt pierwiastkowania sygnału.
