Podstawy Automatyki

Rozdz.5 Człon Różniczkujący

Rozdz.5.1 Wstęp

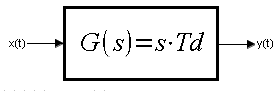
Rys. 5-1
Transmitancja członu różniczkującego, ściślej – idealnego członu różniczkującego
Człon różniczkujący reaguje na prędkość zmiany sygnału x(t), a nie na jego wartość! Jest najlepszą pomocą dydaktyczną do zrozumienia pojęcia pochodnej funkcji, ogólnie rachunku różniczkowego. Przeważnie w transmitancjach G(s) literka s występuje w mianowniku ułamka, natomiast w członie różniczkującym jest zwykłą liczbą (ale zespoloną s jak każda inna w tym artykule).
Przy sterowaniu ręcznym z suwaka przebiegi wyjściowe czlonu różniczkującego są po prostu wredne, jakieś szpile itd… Utrudnia to wyciągnięcie właściwych wniosków. Dlatego przy badaniu tego członu nie będzie schematów z suwakiem i bargrafem.
Człon różniczkujący daje na wyjściu sygnał y(t) proporcjonalny do prędkości zmian sygnału wejściowego x(t), czyli do jego pochodnej.
Dlatego w każdym doświadczeniu upewnij się że tak jest tzn:
Gdy x(t) szybko rośnie–>y(t) jest duże dodatnie
Gdy x(t) jest stałe –> y(t)=0 bo prędkość zerowa
Gdy x(t) szybko maleje–>y(t) jest duże ujemne (prędkość ujemna)

Rozdz.5.2 Sygnał x(t) rośnie liniowo gdy Td=1sek

Rys. 5-2
Rysunek jest w pierwszej chwili taki sam jak dla członu całkującego na Rys. 4-4 w rozdz. 4 . Ale tam na wejściu był skok a na wyjściu piła, a tu jest odwrotnie! Dlatego mówi się że różniczkowanie jest odwrotnością całkowania i vice versa.
Najważniejsze
Dla członu różniczkującego o transmitancji G(s)=s*Td gdy Td=1sek sygnał wyjściowy jest równy prędkości zmian sygnału wejściowego. Prędkość zmian wynosi 1/sekundę i jest stała. Dlatego odpowiedzią na ten sygnał jest stała wartość 1.
Prędkość zmian dowolnej funkcji to pochodna tej funkcji. Tu pochodną liczyło się łatwo, bo prędkość zmian była stała.
Pochodną z x(t) jest y(t). Do trzeciej sekundy y(t)=dx/dt=0 bo x(t)=0 i się nie zmienia, a od 3 sekundy dx/dt=1.
Definicja czasu różniczkowania Td
Po czasie Td=1sek sygnał członu różniczkującego y(t) zrówna się z narastającym sygnałem wejściowym wejściowym x(t). Zauważ, że Td nie zależy od prędkości narastania x(t). Gdy prędkość się zwiększy, to zrównanie też wystąpi po Td=1sec ale przy wyższym poziomie y(t)!
Powtórzmy doświadczenie, ale z 2-krotnie większą prędkością narastania sygnału liniowego.

Rys. 5-3
2-krotne zwiększenie prędkości narastania x(t) spowodowało 2-krotne zwiększenie y(t).
Ale zrównanie x(t) z y(t) też nastąpiło po 1 sek. Człon różniczkujący G(s)=s*Td jest jakby prędkościomierzem sygnału x(t).

Rozdz.5.3 Sygnał x(t) „rośnie, stoi i opada”
Zjawisko znane nie tylko w automatyce.

Rys. 5-4
0…2 sek stałe x(t)=0 dlatego też y(t)=0 (bo „prędkość” x(t) zerowa)
2…4 sek sygnał x(t) rośnie ze stałą (dodatnią) prędkością=1/sek (pochodną!)–> y(t)=+1
4…6 sek sygnał x(t)=1 jest stały czyli ma prędkość=0 –>y(t)=0
6…10 sek sygnał x(t) maleje ze stałą (ujemną) prędkością=-1/sek –> y(t)=-1

Rozdz. 5.4 Sygnał x(t) z dwoma stałymi prędkościami

Rys. 5-5
Dwukrotne zwiększenie prędkości (pochodnej) sygnału wejściowego x(t) spowodował dwukrotny wzrost sygnału wyjściowego y(t).

Rozdz.5.5 Sygnał x(t) z czterema stałymi prędkościami
Za każdym razem prędkość, czyli pochodna sygnału wejściowego x(t) będzie wzrastała o ten sam przyrost prędkości Δx(t)=1/sek

Rys. 5-6
Czterokrotne zwiększenie prędkości (pochodnej) sygnału wejściowego x(t) spowodowało czterokrotny wzrost sygnału wyjściowego y(t).
Sygnał x(t) staje się podobny do paraboli (funkcji kwadratowej) a y(t) do liniowej. Oczywiście z grubsza. A gdyby tak na wejście podać x(t) jako parabolę? Domyślasz się co będzie?

Rozdz.5-7 Sygnał x(t) jest funkcją kwadratowa
A gdyby tych odcinków było 8, 16,…..1024 … nieskończenie dużo to czy otrzymamy idealną parabolę? Sprawdźmy.

Rys. 5-7
Człon różniczkujący potwierdza znany od 17 wieku, wzór na pochodną funkcji kwadratowej.
Sprawdź np. że wzór na pochodną zgadza się dla t=4.

Rozdz.5.7 x(t) jest sinusoidą sin(t)

Rys. 5-8
x(t)=sin(t) y(t)=cos(t)
Sygnał sinusoidalny x(t)=sin(t) został zróżniczkowany przez G(s) dając na wyjściu cosinusoidę.
Cosinusoida jest pochodną sinusoidy.

Rozdz. 5.9 x(t) jest pojedynczym impulsem prostokątnym

Rys. 5-9
W 3 sekundzie sygnał wejściowy x(t) rośnie skokowo. Czyli jego prędkość narastania ma wartość +nieskończoność.
Stąd ta czerwona szpilka y(t) to dirac do +nieskończoności. W 6 sekundzie sygnał maleje do zera skokowo, prędkość ujemna –>czerwona szpilka y(t) to dirac do -nieskończoności. W pozostałym czasie (czyli wszędzie oprócz 3 i 6 sekundy ) x(t) jest stałe. Czyli x(t) ma prędkość zerową. Czyli w tym czasie y(t) też jest zerowe.

Rozdz.5.10 Podsumowanie
Człon Różniczkujący reaguje na prędkość zmian sygnału wejściowego x(t), czyli na jego pochodną x'(t).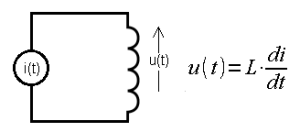

Rys. 5-10
Przykładem jest cewka o indukcyjności L, gdy wejściem x(t) jest prąd i(t) a wyjściem y(t) napięcie na cewce u(t).
Typowym sygnałem wejściowym x(t) do badania większości członów dynamicznych jest skok jednostkowy. Dla członu różniczkującego jest nim jednak sygnał narastający liniowo. Łatwo wtedy z niego otrzymać parametr Td z Rys. 5-1.
Dla skoku jednostkowego –>Rys.5-10 byłoby to, oględnie mówiąc trudniejsze. Dlatego do badania członów różniczkujących najlepiej nadają się narastające sygnały x(t) typu piła.