Szeregi Fouriera klasycznie
Rozdział 4. Wizualizacja zespolonego szeregu Fouriera
Rozdział 4.1 Narzędzie do wizualizacji
Jest ogólnie dostępne i pochodzi z https://betterxplained.com/articles/an-interactive-guide-to-the-fourier-transform. Ułatwia zrozumienie równania na Zespolony Szereg Fouriera z częścią rzeczywistą z Rys.3-12 Rozdział 3. A z niego już bardzo blisko do ogólnego równania na Zespolony Szereg Fouriera z Rys.3-21 Rozdział 3.
Rozdział 4.2 Funkcja stała f(t)=c0=1
Przed kliknięciem pamiętaj, że wrócisz do artykułu klikając windowsową strzałkę powrotu.
Kliknij Badanie zespolonego szeregu Fouriera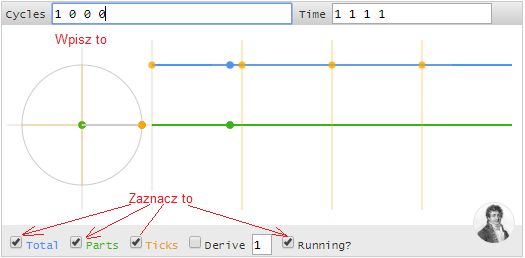
Rys. 4-1
Animacja funkcji f(t)=c0=1
Zaczynamy więc od stałej jako najprostszej funkcji. Zrób co każe obrazek. Tzn wpisz do okna Cycles 1 0 0 0 oraz zaznacz okienka na dole. Do okna Time nic nie wpisuj, bo “samo” się wpisze. Efektem jest nieruchomy żółty punkt na okręgu o promieniu 1 po lewej stronie i poruszający się niebieski punkt po prawej stronie.
W oknie Cycles możesz np. zaprogramować 3 obracające się wektory c1, c2 i c3 z prędkościami 1ω, 2ω i 3ω oraz stałą c0. W następnym rozdziale zmierzysz okres T=3sek najwolniejszego wektora. Oznacza to to, że jego prędkość obrotowa, tzw, pulsacja to ω=2.1/sek
Czyli możesz badać funkcję zespoloną z Rys. 3-8 Rozdział 3 w wersji okrojonej.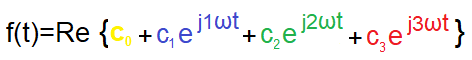
Rys. 4-2
Funkcja zespolona po wpisaniu “1 0 0 0″
Ponieważ wpisałeś do Cycles 1 0 0 0, tzn. c0=1 oraz c1=0 c2=0 i c3=0 to nic się nie obraca! Lub inaczej-formalnie wektor c0 obraca się z prędkością ω=0 a wektory c1, c2, c3 mają długość 0, czyli nie istnieją. Po prawej stronie masz wykres czasowy f(t)=c0=1.
Rozdział 4.3 Funkcja f(t)=1*exp(j1ωt)
Kliknij Badanie Zespolonego Szeregu Fouriera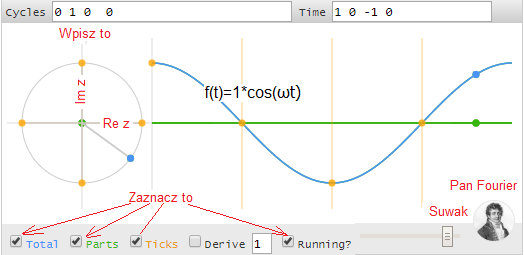
Rys. 4-3
Animacja funkcji f(t)=1*exp(jωt)
Otrzymamy ją po wpisaniu do okna Cycles 0 1 0 0. Wartość funkcji zmienia się w czasie t i jest nią położenie niebieskiego punktu na płaszczyźnie zespolonej. Zobaczysz więc niebieski punkt obracający się z prędkością ω. Jego położenie na płaszczyźnie liczb zespolonych Re z, Im z jest właśnie funkcją zespoloną f(t)=1*exp(jωt).
Rzut punktu na oś Re z porusza się wg. wzoru f(t)=1*cos(ωt) i jest pokazany po prawej stronie.
Cztery fazy tego ruchu tj. ωt=0º,90º,180º,270º wyznaczają żółte punkty po lewej i pionowe żółte kreski po prawej.
Okno Time to wartości 1, 0, -1, 0 funkcji w tych fazach.
Klikając w dowolne miejsce zatrzymasz animację. Może uda Ci się to zrobić w fazach ωt=0º,90º,180º,270º.
Ponowne kliknięcie znowu uruchamia animację. Spróbuj kilka razy, to dojdziesz do mistrzostwa. Przyda się w dalszej analizie.
Po zatrzymaniu możliwe jest przesuwanie punktu suwakiem.
Jeszcze jedno. Zmierz czas t np. 10 obrotów. Powinno być t=30 sek czyli okres T=3sek. Czyli ω=2π/3ek≅2.1/sek.
Rozdział 4.4 Funkcja f(t)=1*exp(j1ωt-30º)
Kliknij Badanie Zespolonego Szeregu Fouriera
Rys. 4-4
Animacja funkcji f(t)=1*exp(jωt-30°)
Po wpisaniu do okna Cycles 0 1:-30 0 0 otrzymamy w.w funkcję zespoloną f(t). Jej wartość zmienia się w czasie t i jest nią to położenie niebieskiego punktu na płaszczyźnie zespolonej. Punkt ten porusza się po okręgu a jego rzut na oś Re z porusza się wg. równania f(t)=1*cos(ωt-30º).
Zauważ, że obracający się niebieski punkt
-jako funkcja zespolona f(t)=1*exp(jωt-30°)
-jako wykres czasowy f(t)=1*cos(ωt-30º)
zawiera tą samą informację. Może opisywać np. przebieg prądu i wtedy obracający się punkt elektrycy nazywają wskazem prądu. Przeważnie wskaz jest wygodniejszy niż wykres czasowy bo lepiej widać amplitudę i fazę.
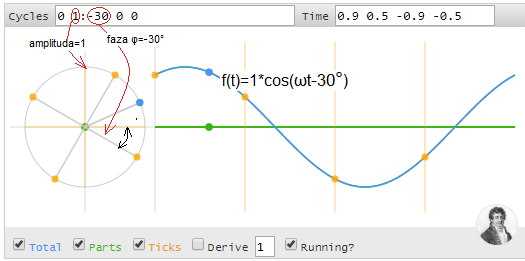
Rozdział 4.5 Funkcja f(t)=c1*exp(j1ωt)+c2*exp(j2ωt)+c3*exp(j3ωt)
Im dalej w las, tym więcej drzew. Zbadajmy więc funkcję f(t)=c1*exp(j1ωt)+c2*exp(j2ωt)+c3*exp(j3ωt) z Rys. 3-6a Rozdział 3 w której:
c1=1-0.2j
c2=0.6-0.4j
c3=0.4-0.4j
Czy otrzymamy ten sam przebieg,czyli z Rys. 3-6b Rozdział 3?
Niestety okno Cycles przyjmuje parametry zespolone c1, c2 i c3 tylko w wersji moduł-faza Czyli zamieniamy
c1=1-0.2i–>r=1.02 φ=-11.301º
c2=0.6-0.4j–>r=0.721 φ=-33.7º
c3=0.4-0.4j–>r=0.567 φ=-45º
Tu proponuję skorzystać z niezawodnego Wolframika Jak chcesz przekształć np. c1=1-0.2i to kliknij WolframAlfa.
Pamiętaj tylko, że liczba urojona w Wolframie to i a nie j.
Rys. 4-5
Jak przekształcić c1=1-0.2i na c1 w formie r=1.02 φ=-11.301º
Rób co każe obrazek.
Po przekształceniu c1, c2 i c3 możesz już badać Szereg Fouriera.
Kliknij Badanie Zespolonego Szeregu Fouriera
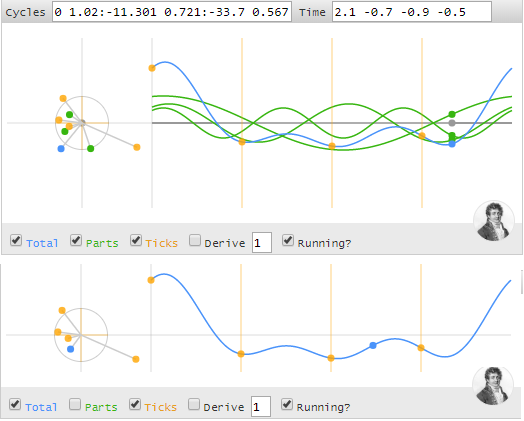
Rys. 4-6
Animacja funkcji 1.02*exp(1ωt-11.301º)+0.721*exp(2ωt-33.7º)+0.567*(3ωt-45°)
Wpisz do okna Cycles “0 1.02:-11.301 0.721:-33.7 0.567:-45”
Pierwsze w oknie Cycles to składowa stała c0=0
Drugie to c1=1-0.2i w wersji r=1.02 φ=-11.301º
Trzecie to c2=0.6-0.4j w wersji 0.721*exp(2ωt-33.7º)
Czwarte to c3=0.4-0.4j w wersji r=0.567 φ=-45º
W oknie Cycles na Rys. 4-6 widzisz tylko 0.567 jako kawałek c3
Górna część rysunku przedstawia 3 harmoniczne i ich sumę (zaznaczono okienka Total i Parts)
Dolna część rysunku przedstawia tylko ich sumę (zaznaczono Total)
Przebiegi są podobne do Rys. 3-6b Rozdział 3. A dlaczego nie identyczne?
Bo są różne skalowania.
Skojarz wirujące wektory z odpowiednimi harmonicznymi, porównaj ich amplitudy i pulsacje. Spróbuj zatrzymać przebieg w fazach 0º, 90º, 180º i 270º. Sprawdź chociaż na oko ich sumy wektorowe i na wykresie czasowym. Powinno się zgadzać.
W ten sposób możesz badać sumę większej ilości harmonicznych tzn więcej niż c0, c1, c2, i c3. 0 ile więcej? Nie wiem.
Możesz teraz sobie wyobrazić Zespolony Szereg Fouriera jako nieskończoną sumę coraz mniejszych i coraz szybciej wirujących wektorów. Ściślej- rzut tej sumy na oś rzeczywistą Re z Rys 3-13 Rozdział 3.
A klasyczna wersja czyli Rys 3-20 i Rys 3-21 Rozdział 3? To suma przeciwsobnie wirujących 2 razy mniejszych wektorów sprzężonych. Na pewno Twoja wyobraźnia sobie z tym poradzi!
