Podstawy automatyki

Rozdz. 3 Człon inercyjny

Rozdz. 3.1 Wstęp
Jest to najprostszy człon dynamiczny poza Proporcjonalnym. Odpowiedź na skok jednostkowy nie jest już natychmiastowa. Możesz nie znać jeszcze pojęcia transmitancji G(s), ale po zakończeniu tego rozdziału będziesz kojarzył jej parametry z przebiegami czasowymi. Do traktowania transmitancji G(s) jako pewnego rodzaju wzmocnienia, nie jest potrzebny rachunek różniczkowy lub operatorowy. Może to było zbyt mocno powiedziane. Lepiej byłoby tak. Znajomość matematyki wyższej nie jest absolutnie konieczna do zrozumienia automatyki , za to bardzo pomocna.

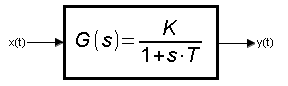
Rys. 3-1
Człon Inercyjny o parametrach:
–K – wzmocnienie w stanie ustalonym
–T – stała czasowa
Wykonamy teraz kilka doświadczeń z różnymi sygnałami wejściowymi. Wyjście będzie obserwowane na bargrafie lub oscyloskopie.

Rozdz. 3.2 K=1 T=5 sek, skok x(t) z suwaka, y(t) na bargraf

Rys. 3-2
Odpowiedź na skok jednostkowy członu inercyjnego K=1 i T=5sek
Sygnał wejściowy x(t) zadany został skokiem 0-1 na suwaku.
Przebiegi możesz obserwować:
analogowo
-x(t)  na suwaku i bargrafie
cyfrowo
-y(t) na miernikach
Mierniki cyfrowe są szczególnie przydatne przy wolnych zmianach po koniec przebiegu.
Uwaga
Sekunda tylko przypadkowo kojarzy się z literką s przy stałej czasowej T.
A co będzie gdy zwiększymy stałą czasową na T=10 sek?

Rozdz. 3.3 K=1 T=10 sek, skok x(t) z suwaka, y(t) na bargraf

Rys. 3-3
Odpowiedź na skok jednostkowy członu inercyjnego K=1 i T=10sek
Porównaj z przebiegiem Rys. 3-2. “Ociężałość” transmitancji jest wyraźnie 2 razy większa.

Rozdz. 3.4 K=1 T=5 sek, skok x(t) z suwaka, y(t) na oscyloskop

Rys. 3-4
Odpowiedź na skok jednostkowy członu inercyjnego K=1 i T=5sek
Sygnał wejściowy x(t) jest skokiem , który wystąpił w 12 sekundzie.
Sygnał wyjściowy y(t) ma największą prędkość wzrostu na początku skoku. Potem rośnie, ale z malejącą prędkością. W stanie ustalonym osiąga wartość y=1.
Na przebiegu dobrze widać, co jest czym w transmitancji G(s) na Rys. 3-4 .
1 w liczniku transmitancji G(s) to wzmocnienie K=y/x=1 w stanie ustalonym.
5 w mianowniku transmitancji to stała czasowa T=5 sekund.
Jest to czas, po którym nastąpiłby stan ustalony y(t)=1, gdyby prędkość wzrostu była cały czas taka sama jak na początku. Sygnał wzrastałby wtedy tak jak styczna – linia kropkowana. Stan y(t)=x(t)=1 zostałby osiągnięty po czasie T=5sek=17sek-12sek.
Czasy 17sek i 12sek odczytasz z osi czasu t.

Rozdz. 3.5 “Wygładzające” działanie członu inercyjnego K=1, T=5sek
Pomachamy suwakiem “wte i we wte”. Czyli sprawdzimy, jak zachowa się człon inercyjny na szybkie zmiany sygnału wejściowego x(t).

Rys. 3-5
Wygładzający efekt członu inercyjnego.
Widzisz ‚wygładzający” efekt członu Inercyjnego. W spadku po Proporcjonalnym pozostały mu „czubki” przy skokowych zmianach sygnału x(t). Takie ma jeszcze człon Całkujący, Opóźniając i Różniczkujący. Pozostałe człony dynamiczne dwuinercyjne, oscylacyjne itd… „czubków” nie mają . Przekonasz się tym później.
Uwaga
Jest stosunkowo duża inercja T=5sek. Dlatego sygnał wyjściowy y(t) jest mało podobny do wejściowego.
Stanie się bardziej podobny gdy:
– sygnał x(t) jest wolnozmienny
– stała czasowa T będzie mniejsza np. T=0.2sek

Rozdz. 3.6 Porównanie dwóch różnych członów inercyjnych
Ten sam skok jednostkowy x(t) będzie podany na 2 różne człony inercyjne.
Tym razem x(t) pochodzi z generatora sygnału, który jest bardziej precyzyjny niż wcześniejszy suwak.

Rys. 3-6
Na wejścia dwóch członów inercyjnych, w których parametry 3 i 7 są „pozamieniane” podawany jest skok jednostkowy x(t).
Na Rys. 3-4 mieliśmy człon inercyjny w którym K=1 i T=5sek. K=1 to było y(t)=1. Pokazaliśmy też jak z wykresu obliczyć T=5sek.
Teraz analogicznie obliczyliśmy K1=7 i T1=3sek dla górnego członu inercyjnego i K2=3 i T2=7sek dla dolnego.

Rozdz. 3.7 Impuls Diraca
Rozdz. 3.7.1 Wstęp
Innym używanym w teorii sterowania sygnałem jest tzw. Impuls Diraca–> x(t) = δ(t). Jego cechą charakterystyczną jest to, że trwa nieskończenie krótko ale ma nieskończenie dużą wartość. Za to energia tego impulsu czyli pole impulsu równe jest jedności czyli jest skończona.
Przybliżeniem może być np elektrownia, która zasila czajnik elektryczny całą swoją mocą (np. 3600 MW), ale przez bardzo krótki czas. Woda w czajniku zagrzeje się do +100°C bo w ciągu kilku nanosekund, zostanie dostarczona skończona energia ( i to wcale nieduża!), a czajnik nie ulegnie zniszczeniu!
Dla nas czajnik zagrzał się natychmiast! Myślimy, że mamy do czynienia z Idealnym Impulsem Diraca.
Mechanicznym przykładem impulsu Diraca jest uderzenie młotkiem. Trwa też bardzo krótko i w tym czasie zostanie wykonana skończona praca polegająca na wbiciu gwoździa.
Wniosek W przyrodzie nie ma idealnych Impulsów Diraca Są tylko jego rzeczywiste przybliżenia.
Rozdz. 3.7.2 Człon inercyjny K=1 T=1sek z rzeczywistym impulsem Diraca

Rys. 3-7
Odpowiedź członu inercyjnego na (prawie) impuls Diraca δ(t)
Impuls o Amplitudzie A=10 i czasie trwania tp=0.1sek jest tylko przybliżeniem idealnego impulsu Diraca δ(t). Widać jak w czasie tp sygnał szybko narasta. Potem opada, gdyż jest 0 na wejściu. Tak wygląda szybkie ładowanie przez opornik R kondensatora C i jego rozładowanie.
Rozdz. 3.7.3 Człon inercyjny K=1 T=1sek z “bardziej idealnym” impulsem Diraca
Poprzedni Dirac o amplitudzie 10 trwał 0.1 sekundy. Skoro nie jesteśmy w stanie dać idealnego Diraca, to dajmy chociaż coś bardziej zbliżonego do ideału. Tzn. Impuls o amplitudzie 100 który będzie trwał 0.01 sek. Zauważ, że jego energia, czyli pole impulsu też wynosi 1.

Rys. 3-8
Odpowiedź członu inercyjnego na (bardziej idealny) impuls Diraca δ(t)
Impuls jest 10 razy wyższy (czyli wynosi 100 i przekracza  zakres oscyloskopu) i  10 razy węższy. Jego pole=1, czyli energia, jest takie samo jak poprzednio. W dalszym ciągu nie jest idealny, chociaż wygląd samego Diraka jest podręcznikowy.

Rozdz. 3.8 Po co nam te Diraki?
Zwłaszcza, że skok jednostkowy jest technicznie łatwiejszy do realizacji niż szpila Diraca. W skoku wystarczy podać maksymalną moc na wejście np. 100 kW. W prawie idealnym Diraku to już jest Bełchatów 4000 MW przez kilka nanosekund. Są techniczne sposoby podania krótkiego impulsu o dużej mocy bez użycia elektrowni, np. zasilacze do laserów, stacje radiolokacyjnych… Ale to już nie jest prościzna.
No właśnie. Po co ten Dirac. Wybiegnę trochę do przodu. Okaże się, że transmitancja G(s) jest po prostu przekształceniem Laplace’a odpowiedzi y(t) na impuls Diraca. Na razie tylko tyle. Transmitancjom G(s), transformatom Laplace’a będzie poświęcony specjalny rozdział.

Rozdz. 3.9 Dwa pozornie różne człony inercyjne 

Rys. 3-9
Ten sam skok jednostkowy x(t) działa jednocześnie na człon inercyjny dolny i górny . Reakcje, czyli y1(t) i y2(t) są identyczne. Czyli obydwa człony inercyjne też są identyczne. Ale w górnym członie nie widać parametrów K=2 i T=3sek.  Aby je zobaczyć zrób tak, żeby w mianowniku górnego było 1+…. Czyli podziel licznik i mianownik górnego przez 7. Okaże się, że obydwa ułamki, czyli G1(s) i G2(s), są to takie same 1/(1+3*s)!
Tę dolna transmitancja jest w wersji znormalizowanej. Łatwo z niej odczytać parametry K=2 i T=3sek. Wszystkie podstawowe człony dynamiczne z rozdz. 2…9 przedstawione są w wersji znormalizowanej. Szczególnie w rozdz. 6 Człon Oscylacyjny.

Rozdz. 3.10 Typowe człony inercyjne
Układ RC
Zaczniemy od przykładu elektrycznego-układu RC. Gdy na wejście podam skok napięcia x(t), to na wyjściu pojawi się napięcie y(t) o takim przebiegu.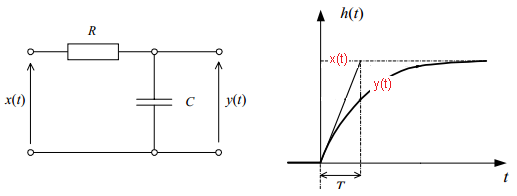

Rys. 3-10
Jest to człon Inercyjny o parametrach k i T k=1 bo w stanie ustalonym y(t) = x(t) Gdy np. R = 100 kΩ i C =10 µF to T = R*C = 100 000 Ω * 10*0,000001F = 1 sekunda
Silnik prądu stałego
Jeżeli na wejście podam skokowo napięcie stałe, to jego rozruch w przybliżeniu jest typowy dla członu inercyjnego. Wejściem jest napięcie a wyjściem prędkość obrotowa. Początkowo prędkość jest zerowa , potem cały czas rośnie, z tym że przyrosty prędkości stają się coraz mniejsze. W końcu osiągnie wartość maksymalną, zależną oczywiście od napięcia wejściowego i parametrów elektro-mechanicznych. Stała czasowa też zależy od tych parametrów- głównie od bezwładności mechanicznej, rezystancji i indukcyjności. Stop! I tak już za daleko weszliśmy w szczegóły.
Wanna z wyjętym korkiem
Wejściem jest „natychmiastowe” otwarcie kranu (czyli pośrednio przepływ)
Wyjściem poziom wody
Na początku poziom jest niski. Czyli ciśnienie i odpływ też są niskie. Dopływ jest większy od odpływu i poziom rośnie. Będzie on jednak narastał coraz wolniej ponieważ ze zwiększającym się poziomem odpływ rośnie (większe ciśnienie). Po pewnym czasie gdy dopływ równy jest odpływowi, poziom ustali się.
Gdyby dokładniej rozpatrzyć równanie różniczkowe tego zjawiska, to odpływ oczywiście rośnie wraz z wysokością, ale nie proporcjonalnie do poziomu lecz do pierwiastka z poziomu. Przy małych poziomach można jednak założyć proporcjonalność i wtedy jest to już klasyczny człon Inercyjny.
Rozdz. 3.11 Podsumowanie
Tak jak człon Proporcjonalny jest pierwszym przybliżeniem prawie każdego członu dynamicznego, tak Inercyjny jest drugim, czyli już dokładniejszym przybliżeniem. Przecież prawie* każdy człon w odpowiedzi na skok po pewnym czasie osiągnie jakąś stałą wartość! Założymy wtedy, że jest to człon inercyjny o wzmocnieniu wynikającym ze stanu ustalonego, i stałej czasowej 4…5 razy mniejszej niż czas ustalenia się sygnału. Będzie to oczywiście przybliżenie kiepskie, ale lepsze to niż przybliżenie członem proporcjonalnym
*prawie– bo nie dotyczy np. członu Całkującego.