Podstawy automatyki

Rozdz. 30 Struktury układów regulacji

Rozdz. 30.1 Wstęp 
Struktury nie zależą od typu regulatora. Może być nim PID, dwupołożeniowy i każdy inny np. nieciągłe odmiany PID-a. Tu mała dygresja do „nieciągłych odmian PID-a”. Czytasz sobie specyfikację regulatora dwupołożeniowego, a tam jak byk jest np. nastawa Kp typowa dla regulatora proporcjonalnego. O co chodzi? Przecież on tylko włącza i wyłącza moc do obiektu. Jakie wzmocnienie może mieć regulator dwupolożeniowy? Ale jeżeli na wyjściu daje falę prostokątną 1 Hz o wypełnieniu proporcjonalnym do uchybu e, a obiekt ma bezwładność rzędu minut, to mamy do czynienia ze sterowaniem prawie ciągłym!  W ten sposób mamy regulator dwupołożeniowy , który działa jak proporcjonalny. Mało tego. Mogą być regulatory dwupołożeniowe typu PID z nastawami Kp, Ti, D. Najbardziej typowym przedstawicielem nieciągłych PID jest tzw. regulator krokowy. Jest on najczęściej stosowany w regulacji przepływu i służy do sterowania stopniem otwarcia zaworu. Tu regulator dochodzi do wartości ustalonej działając na siłownik sygnałem np. napięciowym +max, 0, -max  skokami, inaczej-krokami (zwiększaj, stój, zmniejszaj). W sumie chociaż sygnał sterujący jest nieciągły, to na skutek dużych bezwładności obiektu jego odpowiedź jest ciągła.
Wróćmy jednak do tematu.
Zbadamy typowe struktury układów regulacji:
1– Otwarty
2– Otwarty z Kompensacją
3– Zamknięty
4– Zamknięty z Kompensacją
5– Układ Kaskadowy
6– Układ Regulacji Stosunku

Rozdz. 30.2 Układ otwarty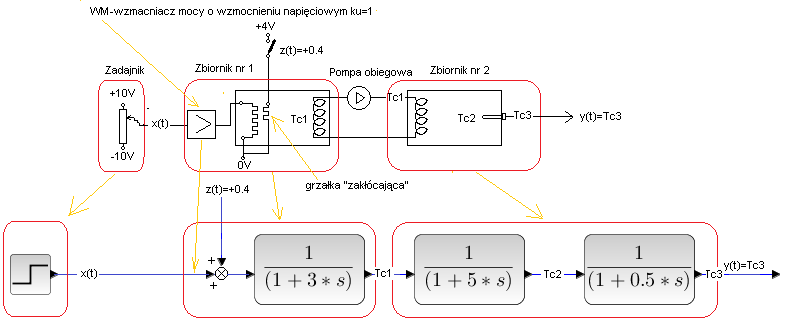

Rys. 30-1
Przykładem jest powyższy schemat sterowania wymiennika ciepła. Dla analizy wygodnie jest, gdy człon wykonawczy wchodzi w skład wymiennika – obiektu Go(s). Tu członem wykonawczym jest wzmacniacz mocy z grzałką. Układ otwarty ma pewne plusy, że tak powiem dodatnie-prostota i zawsze jest stabilny. Za to jest zupełnie nieodporny na zakłócenia z(t). Zakłóceniem z(t)=+0.4 jest skok napięcia +4V spowodowany zwarciem styku na grzałce „zakłócającej”.
Każdy poważny regulator ma przełącznik A/R – praca Automatyczna/Ręczna.
Praca automatyczna A to wersja Rys. 29-7 z rozdz. 29.
Praca ręczna R to układ otwarty, czyli powyższy rysunek.
Wtedy na Rys. 29-7 z rozdz. 29 wejście minus do regulatora zostało podłączone do 0V, a sam regulator PID zmieni swoją strukturę regulator P o Kp=1.  Innymi słowy pętla sprzężenia zwrotnego została przerwana i powstał układ otwarty czyli Rys. 30-1.
Praca ręczna stosowana jest w czasie rozruchu obiektu, w sytuacjach awaryjnych i innych nietypowych.
Przełącznik A/R może być zwykłym przełącznikiem lub tylko programowym. Wtedy operator przełącza A/R z klawiatury. Zapewnia łagodne przejście z jednego trybu w drugi i vice versa. Jest to jakoś tam zrealizowane, ale nie będę wchodził w szczegóły.
Co będzie gdy w 3 sek przesuniemy suwak zadajnika z 0 V na +10V, a w 40 sek podamy skok +4V na grzałkę „zakłócającą”?
Uwaga
Większość regulatorów realizowana jest w wersji cyfrowej . Inaczej dodawanie, odejmowanie mnożenie dzielenie, całkowanie i różniczkowanie obliczane przez mikroprocesor a nie analogowo.

Rys. 30-2
Tak jakbyś gwałtownie przesunął suwak z 0V na +10V, a potem w 40 sek podał skokowo napięcie +4V na grzałkę zakłócającą. Odpowiedź y(t) jest oczywista. Skutkiem skoku x(t) jest stan y(t)=Tc3=+100ºC po 35 sek i stan y(t)=Tc3=+140ºC po 75 sek
Przypominam,  że rozdz.29.3.2 „uprościliśmy” elektrotechnikę. Moc wydzielana na grzałce jest proporcjonalna do napięcia, a nie do kwadratu napięcia.

Rozdz. 30.3 Układ otwarty z kompensacją
Rozdz. 30.3.1 Wstęp
Co zrobić żeby Układ Otwarty nie miał „absolutnego braku odporności na zakłócenia”. Rozwiązaniem może być dodanie kompensacji. Spróbujmy ograniczyć wpływ zakłócenia poprzez kompensację zakłócenia. Zawsze do czegoś nowego podchodzi się ostrożnie jak pies do jeża. Dlatego na początek damy kompensację niepełną k=0.7.
Rozdz. 30.3.2 Układ Otwarty z Kompensacją Niepełną k=0.7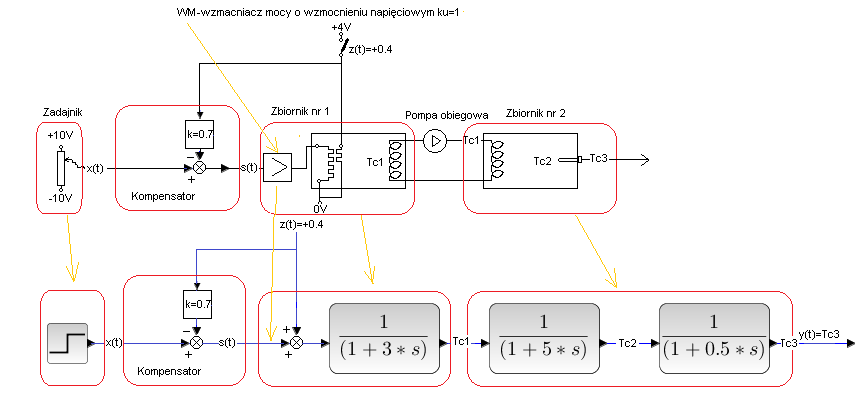

Rys. 30-3
Powyższy schemat to w skrócie Rys. 30-1 + dodatkowy blok kompensator. Mierzy on napięcie (czyli zakłócenie z(t)=+0.4 ) a następnie oblicza sygnał sterujący s(t)=x(t)-k*z(t) który podawany jest na wejście obiektu. Sygnał sterujący s(t) dzięki operacji odejmowania ma przeciwny kierunek działania niż zakłócenie z(t). Jeżeli zakłócenie grzeje (tak jak schemacie) to s(t) zmniejsza dopływ mocy do grzałki czyli chłodzi. Jeżeli zakłócenie chłodzi, to s(t) dodatkowo grzeje. Kompensator pełni więc funkcję regulatora.
Niektórzy nazywają to regulatorem ze sprzężeniem w przód inaczej feedforward controller. Dziwny to regulator. Nie korzysta z sygnału wyjściowego y(t), tylko z sygnałów wejściowych tj:
– x(t) (co jest normalne dla każdego regulatora!)
– zakłócenia z(t) (na tym polega dziwota).

Rys. 30-4
Odpowiedź na x(t), czyli przebieg y(t) w czasie 3…40 sek, jest oczywista. W 40 sek nastąpiło zakłócenie z(t)=+0.4 – dodatkowe grzanie. Sygnał sterujący s(t) zareagował prawidłowo, zmniejszył grzanie o 0.7*0.4=0.28 do wartości 0.72. W sumie dostarczona jest moc 0.72+0.28=1.12, która odpowiada temperaturze w stanie ustalonym y(t)=+112ºC. W porównaniu do Rys. 30-2, gdzie nie było żadnej kompensacji, nastąpiło częściowe stłumienie zakłócenia z(t). Nie trzeba być geniuszem, żeby przewidzieć efekt pełnej kompensacji. Pełne tłumienie zakłócenia z(t) zapewni tylko pełna kompensacja k=1.
Rozdz. 30.3.3 Układ otwarty z kompensacją pełną k=1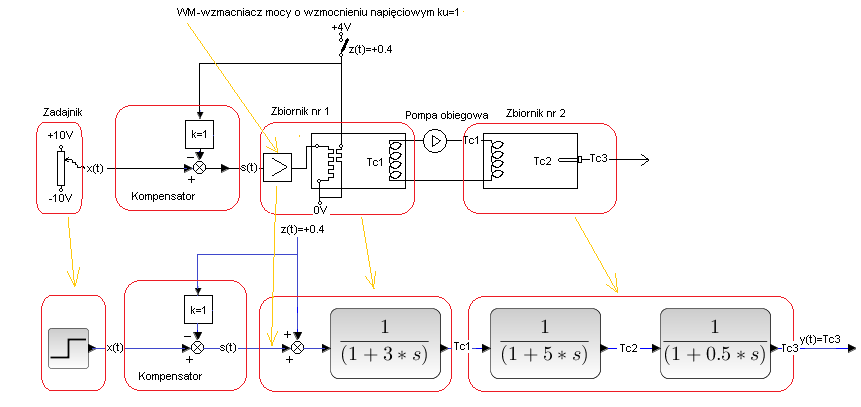

Rys. 30-5
Współczynnik kompensacji k=1. Domyślasz się chyba efektu pełnej kompensacji?

Rys. 30-6
Sygnał sterujący s(t) jest teraz w przeciwfazie do z(t) i nastąpiła pełna kompensacja zakłócenia. Sygnał wyjściowy y(t) pomimo zakłócenia z(t)=+0.4 (dodatkowe grzanie) ani drgnie. Stoi jak lanca ułańska. Tu powstają 2 pytania?
1– Dlaczego od razu nie daliśmy współczynnika kompensacji k=1?
2– Skoro nastąpiło 100% tłumienia zakłócenia, to dlaczego nie jest to metoda uniwersalna.
Odpowiedź na 1
Nam było łatwo, bo znamy transmitancję obiektu Go(s) i k=1 było oczywiste. Ale na prawdziwym obiekcie, np w Rafinerii Gdańskiej, nie widzisz transmitancji, tylko jakąś kolumnę, rurociągi grzewcze i te nie do końca rozpracowane sygnały „zakłócające”. Nawet gdy masz na regulatorze potencjometr kompensacji np. k=0…1.5 to idealną wartość dobierzesz albo doświadczalnie kręcąc potencjometrem, albo teoretycznie, gdy masz dokładnie rozpracowany matematycznie obiekt. Powracając zaś do „potencjometru k” to w poważnych układach występuje on tylko jako software. Operator „kręci” nim poprzez klawiaturę, wprowadzając do systemu odpowiednie liczby.
Uwaga*
Wcześniej były już układy, gdzie pomimo zakłócenia z(t) regulator PID pracował tak, że czerwone y(t) „stało” w miejscu. Wynikało to jednak tylko z małego wzmocnienia oscyloskopu. Gdyby było większe to czerwone y(t) „ruszałoby” się.
Odpowiedź na 2
Rzeczywiście. Dotychczas nie spotkaliśmy się z tak idealnym tłumieniem zakłócenia. Ale kompensacja udaje się tylko wtedy, gdy dobrze znamy obiekt, da się zmierzyć zakłócenie z(t) oraz parametry obiektu są stałe w czasie. A nie zawsze tak jest. Poza tym układ nie jest odporny na inne zakłócenia! Dlatego w p. 30.5 poznasz Układ Zamknięto-Otwarty, w którym występuje kompensator tłumiący zakłócenie mierzone i zwykłe sprzężenie zwrotne tłumiące pozostałe zakłócenia.
Rozdz. 30.3.4 Układ otwarty z kompensacją „zwykłą” zakłócenia „w środku” obiektu Go(s)
Zakłócenie w „środku obiektu”, ale kompensator k=1. Tak jak na poniższym schemacie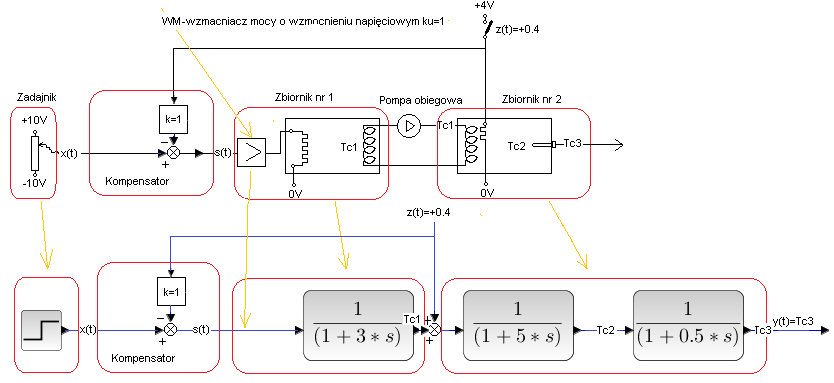

Rys. 30-7
Grzałka „zakłócająca” jest tuż przy wężownicy zbiornika nr 2. Spodziewamy się, że zakłócenie z(t) będzie w jakimś stopniu skompensowane. Odpowiedź powinna być lepsza niż w układzie bez kompensacji z Rys. 30-2. Ale czy tak dobra jak na Rys. 30-6 z zakłóceniem na początku obiektu?

Rys. 30-8
W czasie 3…40 sek sygnał wyjściowy y(t)=Tc3 jest taki sam jak na Rys. 30-3,6 i 9 bo nie było jeszcze zakłócenia. W 40 sek wystąpiło z(t)=+0.4 od grzałki „zakłócającej”. Kompensator zareagował prawidłowo obniżając sygnał sterujący s(t) też 0.4 – w przeciwfazie. Ale tym razem widać wpływ zakłócenia z(t). Co prawda przejściowy. Dlaczego?
Bo spadek dopływu mocy grzejnej do zbiornika 2 nie nastąpił skokowo, tylko z inercją 3 sek, tak jak temperatura Tc1 w zbiorniku 1 równa temperaturze cieczy w wężownicy zbiornika 2. Po 65 sek. sygnał wyjściowy wrócił znowu do stanu początkowego y(t)=+100ºC. Kompensastor spełnił w końcu swoje zadanie, choć nie tak chwalebnie jak na Rys. 30-5, gdzie z(t) działało bezpośrednio na wejście. Wtedy zakłócenie zostało stłumione idealnie natychmiast przez spadek mocy grzejnej grzałki w zbiorniku 1.
Jest dobrze, ale chcemy żeby było jeszcze lepiej. Jak? Można np. dać dodatkową grzałkę elektryczną z elementem Peltiera tuż przy grzałce zakłócającej. Wtedy ujemne napięcie na Peltierze spowoduje chłodzenie , czyli spowoduje natychmiastowy spadek mocy cieplnej dostarczanej do zbiornika 2. Jest to jakieś rozwiązanie, ale wiąże się to z dodatkową strukturą i kosztami, pogorszeniem sprawności energetycznej.
Można też wykorzystać istniejącą grzałkę w zbiorniku 1. Zauważ, że niedoskonałość tłumienia zakłócenia z(t)=+0.4 wynika z tego, że transmitancja zakłóceniowa między z(t) a sk(t), to Gzk(s)=1/(1+sT) gdzie T=3 sek. Jest to więc człon inercyjny o stałych k=-1 i T=3 sek. A gdyby zrobić z niego człon proporcjonalny Gzk(s)=1? Wtedy możliwe byłoby całkowite stłumienie zakłócenia, tak jak na Rys. 30-5. Tylko jak to zrobić?

Rozdz. 30.3.5 Transmitancja „odwrotna”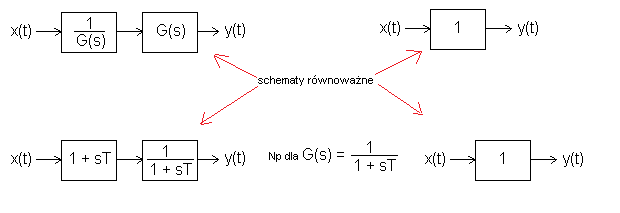

Rys. 30-9
Jak z dowolnego członu G(s) zrobić proporcjonalny G(s)=1?
Teoretycznie jest to bardzo proste. Należy przed G(s) dać jej odwrotność. Tak jak 2 wzmacniacze połączone szeregowo o w wzmocnieniach k1=0.1 i k2=10 dają wzmocnienie k=k1*k2=1.
A jak to wygląda gdy G(s) jest np. członem inercyjnym?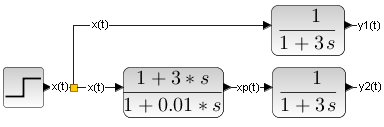

Rys. 30-10
Z członu inercyjnego G(s)=1/(1+3*s) chcemy zrobić człon proporcjonalny G(s)=1. Tak jak pokazaliśmy na Rys. 30-9, należy połączyć go szeregowo z odwrotnością G(s) czyli z członem (1 + 3s). Zaraz zaraz,. a co tu robi w mianowniku (1 + 0.01s)? A no właśnie. Trudno jest zrealizować idealny (1 + 3s). On jako odpowiedź na skok x(t) daje nieskończoność, bo prędkość narastania skoku też jest nieskończona.
Dlatego damy w mianowniku 1 + 0.01s. Odpowiada to szeregowemu połączeniu (1 + 3s) z członem inercyjnym o bardzo małej stałej czasowej T=0.01 sek, tj. 1/(1 + 0.01*s) . Odpowiedź y2(t) na skok x(t) powinna być „prawie skokiem”, a nie idealnym skokiem. Sprawdźmy.

Rys. 30-11
– y1(t) odpowiedź członu inercyjnego
– y2(t) odpowiedź członu “prawie” proporcjonalnego G(s)=1 jako iloczynu członu inercyjnego i jego odwrotności.
Uwaga!
Za chwilę okaże się on członem „prawie proporcjonalnym”.
W pierwszej chwili y2(t) idealnie pokrywa się ze skokiem x(t). Ale jak się dobrze przyjrzysz, to czerwone y2(t) w 1 sekundzie nie pokrywa się ze skokiem x(t). Następuje raczej bardzo szybki wzrost do y2(t) jak w członie inercyjnym o bardzo małej stałej czasowej. Tu właśnie jest wpływ (1+0.01*s) w mianowniku! Dlatego y2(t) jest odpowiedzią członu „prawie proporcjonalnego”.
A dlaczego y2(t) rośnie w czasie skoku bardzo szybko w porównaniu do odpowiedzi y1(t) samego członu inercyjnego? To spójrz jaki potężny jest sygnał xp(t) na wejściu członu inercyjnego. Sygnał xp(t) jest ucięty przez oscyloskop, ale  osiąga wartość xp(t)=301! Potem bardzo szybko spada do 1. Taki przebieg xp(t) jest przyczyną bardzo szybkiego wzrostu sygnału y2(t) do wartości y2(t)=1.
Wniosek:
W liczniku członu kompensującego pojawił się element różniczkujący, który powoduje duże przesterowania –> xp(t)=301! Wymaga to dostarczenia dużych mocy chwilowych, co może być dość kłopotliwe. Jeszcze silniejsze różniczkowania- czytaj drugie i wyższe pochodne, występują przy bardziej bardziej skomplikowanych obiektach niż inercyjne.  Mimo tego kompensacja często poprawia tłumienie zakłóceń, nawet przy ograniczeniach napięć zasilających. Zwłaszcza przy prostych obiektach dynamicznych.
Rozdz. 30.3.6 Układ z kompensacją „odwrotną” zakłócenia „w środku” obiektu Go(s)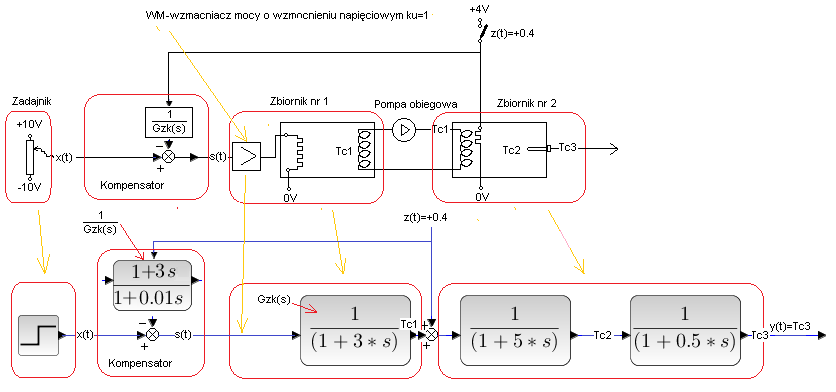

Rys. 30-12
Na dole jest model układu . Jedyna różnica to mianownik kompensatora (1 + 0.01*s) wprowadzający niewielką inercję. Zapobiega ona dirakom-dużym szpilkom przy skokach. Szpilka pozostanie, ale o skończonej wartości! Nie wpływa wyraźnie negatywnie na tłumienie zakłócenia z(t). Umówmy się więc, że jest to kompensacja odwrotna, chociaż formalnie nie jest.

Rys. 30-13
Do zakłócenia z(t)=+0.4 w 40 sek człon kompensujący nie włączył się jeszcze do akcji, czyli przebiegi są takie same jak na Rys. 30-11. Wyraźnie widać jak skok x(t) wyprzedza Tc1 a Tc1 wyprzedza y(t)=Tc3. Przypominam, że Tc1 jako temperatura w wężownicy zbiornika 2 jest sygnałem wejściowym do tego obiektu a y(t) (temperatura mierzona termometrem) jest sygnałem wyjściowym. W 40 sek pojawiło się zakłócenie z(t)=+0.4 (dodatkowe grzanie) ale y(t) nawet nie drgnęło! Super, porównaj to z Rys. 30-8 gdzie była kompensacja „zwykła”, inaczej “bez odwrotnej transmitancji”. Tu mały komentarz. Trochę  jednak „drgnęło”, bo nie jest to idealna kompensacja odwrotna. Po prostu nieczuły oscyloskop tego nie pokazuje a poza tym „ucina”.  Sygnał sterujący s(t) dostał ujemnego kopa w 40 sek –>ujemna szpila ok -120! To efekt różniczkowana członu kompensującego. I tylko dzięki niewielkiej inercji (mianownik członu kompensującego) szpila nie jest dirakiem o sygnale minus nieskończoność. Tak naprawdę to szpila jest trochę rozciągnięta w czasie jak na Rys. 30-11. A dół tej szpili s(t)=-120 musisz sobie wyobrazić. Kilka metrów poniżej osi t, czyli w piwnicy pod podłogą.

Rys. 30-14
Dzięki kompensatorowi  sygnał wejściowy s(t), (a właściwie jego ujemna “chłodząca” szpilka Rys. 30-13), temperatura Tc1 wężownicy będzie prawie “ujemnie prostokątna”. A ta prawie idealnie skompensuje zakłócenie z(t)=+0.4. Przypominam, że Tc1  jest sygnałem wejściowym dla zbiornika 2. To wszystko wynika z animacji Rys. 30-13. A jeszcze bardziej na Rys. 30-14 gdzie są tylko przebiegi Tc1 i z(t)=+0.4.

Rozdz. 30.4 Układ zamknięty
Jest to najczęściej stosowany schemat regulacji. Można powiedzieć, że każdy inny jest tylko jego modyfikacją.
Na przykład:
–Układ Otwarty to Układ Zamknięty z przerwaną pętlą
–Układ Zamknięty z Kompensacją to  Układ Zamkniętu + Kompensacja
–Regulacja Kaskadowa to kombinacja dwóch Układów Zamkniętych.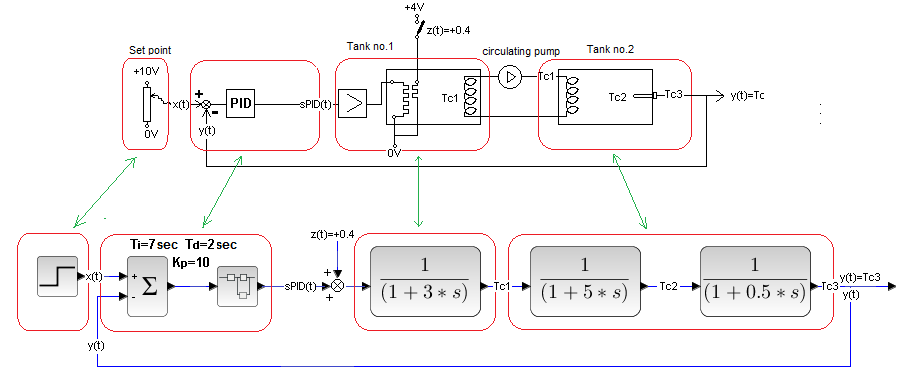

Rys.30-15
Układu Zamknięty.
Jest to kopia schematu z Rys. 29-10 z rozdz. 29. Obiekt otwarty-Wymiennik Ciepła sterowany z potencjometru 0…+10V, został zamknięty pętlą ujemnego sprzężenia z regulatorem PID. Na tym kończę temat, bo właściwie cały kurs dotyczy Układów Zamkniętych .

Rozdz. 30.5 Układ Zamknięty z kompensacją – inna nazwa to Układ zamknięto-otwarty
Rozdz. 30.5.1 Wstęp
Układ Otwarty z Kompensacją potrafi całkowicie stłumić zakłócenie z(t), które da się zmierzyć tak jak na Rys. 30-5. Jest on oczywiście nieodporny na pozostałe niekompensowane zakłócenia, np. na grzałkę „zakłócającą” przy wężownicy w zbiorniku 2. Rozwiązanie narzuca się samo. Należy zamknąć układ pętlą sprzężenia zwrotnego z regulatorem PID. Spodziewamy się, że spowoduje to idealne tłumienie zakłócenia z pełną kompensacją oraz zwykłe tłumienie pozostałych zakłóceń.
Zbadamy różne kombinacje:
– Kompensacja Pełna k=1 z zakłóceniem na wejściu obiektu –>p. 30.5.2
– Kompensacja Niepełna k=0.7 z zakłóceniem na wejściu obiektu–> p. 30.5.3
– Kompensacja Pełna k=1 z zakłóceniem w „środku” obiektu–>p. 30.5.4
– Kompensacja Pełna k=1 z zakłóceniem na wejściu obiektu i z dodatkowymi zakłóceniem w „środku” obiektu–>p. 30.5.5
Rozdz. 30.5.2 Kompensacja pełna k=1 z zakłóceniem na wejściu obiektu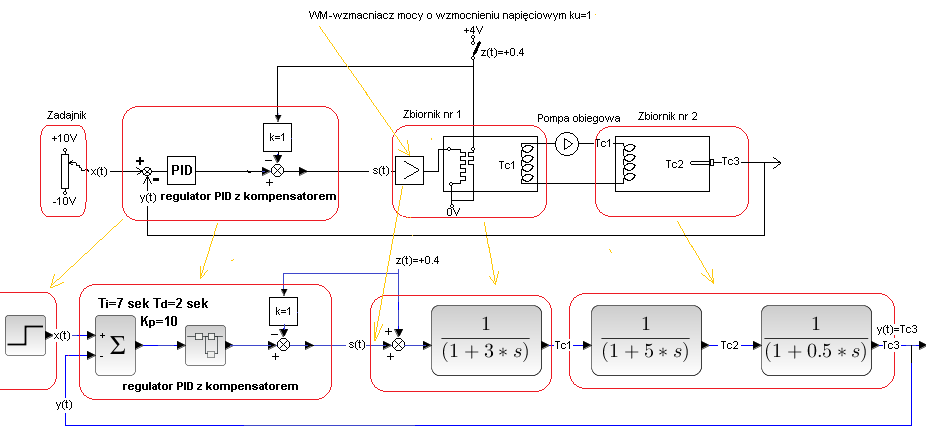

Rys. 30-16
Układ z Pełną Kompensacją z Rys. 30-7 po zamknięciu pętlą z regulatorem PID.
Nastawy Kp, Ti, Td zapewniają optymalną odpowiedź na skok x(t).

Rys. 30-17
Do zakłócenia z(t)=+0.4 w 40 sek odpowiedź na skok x(t) jest identyczna jak Układu Zamkniętego–>Rys. 29-11 z rozdz. 29.
W 40 sek zakłócenie z(t)=+0.4 spowodowało natychmiastową reakcję kompensatora w przeciwfazie w postaci spadku sygnału s(t) też o 0.4. Zakłócenie z(t) zostało więc całkowicie skompensowane. Sygnał wyjściowy y(t) nawet nie drgnął (bo PID „myśli”, że nie było żadnego zakłócenia!) i uchyb e(t) dalej pozostał zerowy.
Sygnał sterujący s(t) jest sumą z regulatora PID–>sPID(t) i sygnału kompensatora. Na z(t)=+0.4 zareagował tylko sygnał z kompensatora.
Rozdz. 30.5.3 Kompensacja niepełna k=0.7 z zakłóceniem na wejściu obiektu
Staramy się żeby wszystko było idealne, także kompensacja. Ale nie zawsze się uda, są różne przyczyny. Zakłócenie z(t) może być np. trudne do zmierzenia… Odpowiada to właśnie przypadkowi gdy np. k=0.7 a nie k=1.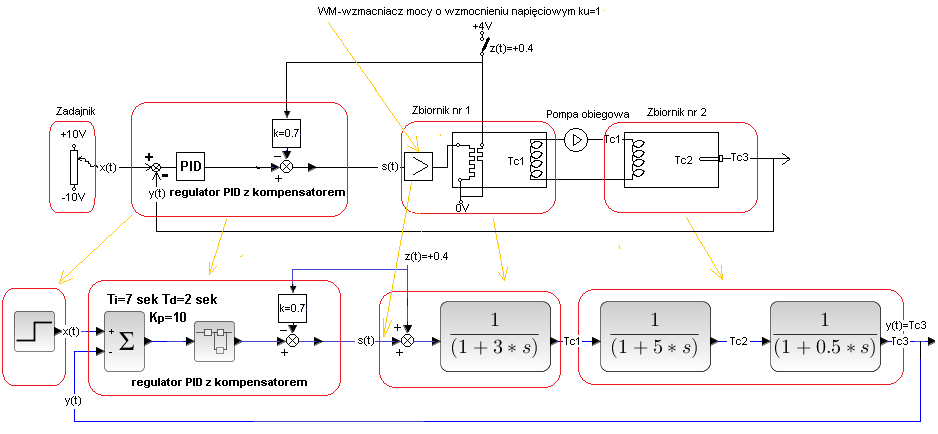

Rys. 30-18
Prawie kopia Rys. 30-16. Jedyna różnica to k=0.7 a nie k=1. Spodziewamy się więc, że będzie jakiś wpływ zakłócenia na wyjście y(t)

Rys. 30-19
Do 40 sek odpowiedź na skok x(t) jest oczywiście taka sama jak poprzednio. Natomiast od 40 sek tylko część zakłócenia z(t)=+0.4 tj 0.7*0.4=0.28 jest natychmiast kompensowana przez kompensator. Pozostała część tj 0.4-0.28=0.12 tłumiona jest PID-em i dlatego nie natychmiast! Trwa to ponad 10 sek co widać na przebiegu s(t). W sumie y(t) nie jest idealnie stłumione jak z pełną kompensacją, za to jest wyraźnie lepiej niż układzie ze sprzężeniem zwrotnym bez kompensacji –>Rys. 29-11 z rozdz. 29. Odpowiedź jest taka, jakby to był układ ze sprzężeniem zwrotnym bez kompensacji, za to z mniejszym zakłóceniem. z(t)=+0.12 ( a nie z(t)=+0.4)
Rozdz. 30.5.4 Kompensacja pełna k=1 z zakłóceniem w „środku” obiektu
Powstanie gdy otwarty Układ z Kompensacją „Odwrotną” z Rys. 30-12 zamkniemy pętlą sprzężenia zwrotnego z regulatorem PID.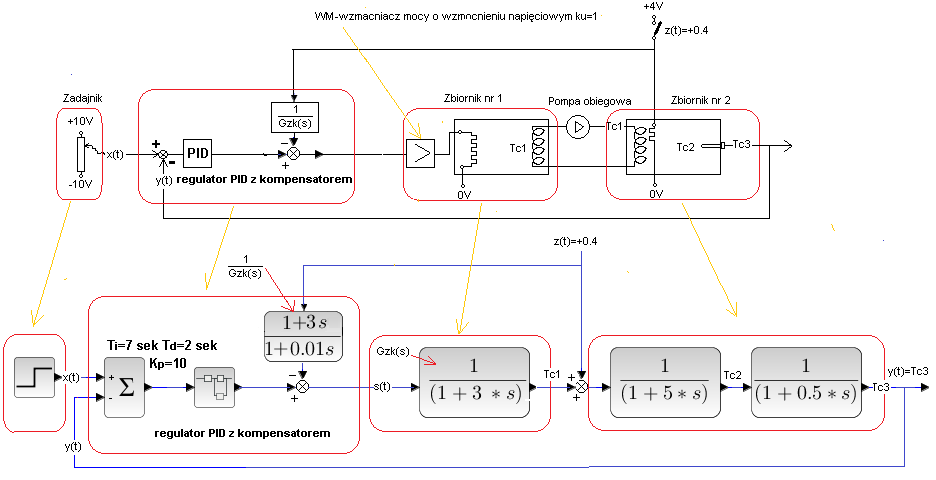

Rys. 30-20
Układ zamknięty z kompensacją pełną z zakłóceniem w środku obiektu.

Rys. 30-21
Do zakłócenia z(t)=+0.4 w 40 sek odpowiedź na skok x(t) jest identyczna jak dla Układu Zamkniętego–>Rys. 29-11 z rozdz. 29.. Po prostu w tym czasie z(t)=0, czyli „część kompensująca” nic nie robi. W 40 sek pojawiło się z(t) przy wężownicy zbiornika 2 które zostało natychmiast* skompensowane przez sygnał sk(t)=Tc1. Dlatego z(t)=+0.4 nie zostało „zauważone” przez PID-a i odpowiedź y(t) jest taka jak dla układu zamkniętego bez zakłócenia!*
Uwaga
W 40 sekundzie pojawia się ujemna szpila s(t), dokładnie tak jak na Rys. 30-13.  Dzięki temu sygnał temperatury jest prawie idealnie prostokątny. Oscyloskop tego nie pokazał.

Rozdz. 30.5.5 Kompensacja pełna k=1 z zakłóceniem na wejściu obiektu i z dodatkowymi zakłóceniem w „środku” obiektu
Będzie to Układ zamknięty z pełną kompensacją z p. 30.5.2 z dodatkowym niekompensowanym zakłóceniem. Zakłócenie kompensowane typu grzanie z1(t)=+0.4 pojawi się jak zwykle w 40 sek. a zakłócenie niekompensowane typu chłodzenie z2(t)=-0.6 w 55 sek.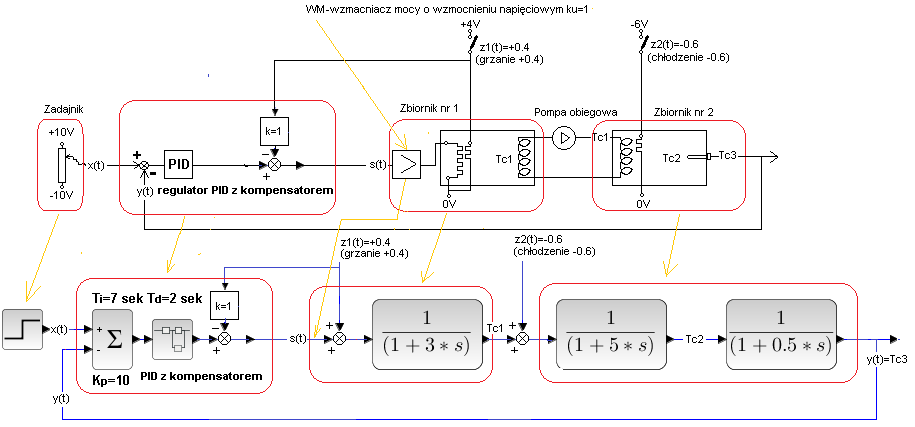

Rys. 30-22
Zakłócenie chłodzące z2(t)=-0.6 tuż przy wężownicy zbiornika 2 spowodowane jest ujemnym skokiem napięcia -6V w 55 sek. Przypominam, że grzałka jest tzw. elementem Peltiera, w którym napięcie dodatnie grzeje a ujemne chłodzi.

Rys. 30-23
Do chwili zakłócenia z1(t)=+0.4 w 40 sek odpowiedź na skok x(t) jest identyczna jak dla Układu zamkniętego (bez kompensacji). Po prostu w tym czasie z1(t)=0, czyli „część kompensująca” nic nie robi, tak jakby jej nie nie było. W 40 sek pojawiło się dodatkowe grzanie z1(t)=+0.4, które zostało natychmiast skompensowane przez sygnał s(t). Dlatego samo y(t) się nie zmieniło i regulator PID nawet nie zareagował. Czyli do tego czasu układ zachowuje się tak jak w Rozdz. 30.5.2.
Jeżeli zaś chodzi a zakłócenie „chłodzące” z2(t)=-0.6, to jako nieskompensowane zostało ono stłumione zwykłym sprzężeniem zwrotnym przez PID-a. Z tym że dla samego PID-a to było tylko zakłócenie z2′(t)=-0.6+0.4=-0.2 ! Bo samym zakłóceniem z1(t)=+0.4 zajęła się już wcześniej część kompensacyjna k=1 regulatora.
Rozdz. 30.5.6 Wnioski
1. Układ Zamknięty z Kompensacją może teoretycznie(!) idealnie stłumić zakłócenie pod warunkiem:
– dokładnego pomiaru zakłócenia
– dobrania odpowiedniej transmitancji kompensatora. Wiąże się to z dokładną znajomością obiektu Go(s).
Gdy zakłócenie jest na wejściu obiektu to transmitancją kompensatora jest k=1–>p.30.5.2
Gdy zakłócenie jest w „środku” obiektu to jest transmitancja odwrotna 1/Gzk(s)–>p.30.5.4
2. Nawet gdy nie uda się dokładnie zmierzyć lub dobrać idealnego kompensatora, to znacznie poprawia się jakość sterowania.–>p.30.5.3. Dotyczy to także transmitancji odwrotnej, gdy zakłócenie jest w „środku” obiektu.
3. W transmitancji odwrotnej pojawia się s w liczniku (powodujące silne różniczkowanie sygnału. Jest to trudne do zrealizowania (nieskończona moc chwilowa) i dlatego rezultaty praktyczne nie są tak piękne jak w naszych eksperymentach. Ale nawet wtedy wyraźna jest poprawa jakości sterowania.
4. Pozostałe nieskompensowane zakłócenia tłumione są PID-em przez zwykłe sprzężenie zwrotne–>p.30.5.5

Rozdz. 30.6 Układ kaskadowy
Rozdz. 30.6.1 Wstęp
Układ umożliwia lepsze tłumienie konkretnego zakłócenia niż klasyczny Układ zamknięty i trochę gorsze niż Układ zamknięty z kompensacją. W odróżnieniu od tego ostatniego, nie wymaga pomiaru zakłócenia, ani tak dokładnej znajomości obiektu Go(s).
Zasada jest podobna do organizacji przedsiębiorstwa. Dyrektor wyznacza kierownikowi podległemu mu oddziału zadanie do spełnienia i przestaje się tym interesować. Nie wnika w zakłócenia działają na oddział, czy Kowalski przyszedł pijany albo klient nie zapłacił faktury. Dla dyrektora plan miesięczny ma być wykonany i kropka. Informacja o zakłóceniu szybciej dochodzi do kierownika niż do dyrektora i dlatego ma on większe możliwości ich tłumienia. Zastosuje metodę kija (groźba zwolnienia) i marchewki (premia). Kierownik szybciej zlikwiduje zakłócenie niż dyrektor. W Układzie Kaskadowym rolę dyrektora pełni regulator nadrzędny-najczęściej PID, a kierownikiem jest regulator podrzędny-przeważnie typu P.
Rozdz. 30.6.2 Układ kaskadowy z jednym zakłóceniem
Ściślej z zakłóceniem a nawet kilkoma działającymi na pewną część obiektu.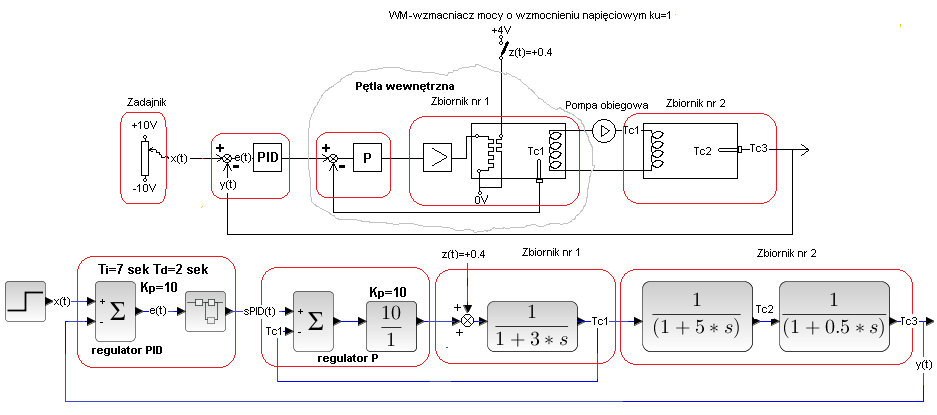

Rys. 30-24
Układ kaskadowy z zakłóceniem
Regulator P porównuje temperaturę Tc1 cieczy zbiornika 1 z sygnałem wyjściowym PID-a. Powstała więc pętla wewnętrzna – zwykły układ zamknięty, w którym sygnał wyjściowy Tc1 „stara” się naśladować sygnał z PID-a.
Wyraźnie widać który regulator jest dyrektorem całej firmy – 2 zbiorników, a który tylko kierownikiem zbiornika nr 1.
Czyli PID jest regulatorem nadrzędnym a P podrzędnym. Czasami podrzędnym jest PI a nawet PID.
Zakłóceniem z(t)=+0.4 jest włączenie dodatkowej grzałki umieszczonej przy grzałce sterującej zbiornika 1. Porównaj ten schemat ze zwykłym Układem Zamkniętym z Rys. 29-10 rozdz.29 . Gdy przerwiemy wewnętrzną pętlę sprzężenia zwrotnego od Tc1 i zamiast regulatora P damy goły drut, to otrzymamy zwykły układ zamknięty. Z Rys. 29-11 rozdz.29 wynika, że zakłócenie zwykłego układu zamkniętego zostało całkowicie stłumione.
A czego się spodziewać od Układu Kaskadowego?
Po pierwsze
– Zmniejszy się bezwładność zbiornika 1, który został objęty silnym sprzężeniem zwrotnym –>Kp=10. Dlatego zmniejszy się też bezwładność całego obiektu i stanie się on łatwiejszy do sterowania. Powinien więc dać krótszy czas odpowiedzi na skok x(t) niż zwykłe sprzężenie zwrotne.
Po drugie – Radykalnie poprawi się tłumienie zakłócenia z(t). Zanim zareaguje PID, to dużo szybciej zrobi to regulator P! Przecież ma on tylko do czynienia z jedną inercją zbiornika nr 1.
Powiem więcej. Regulator P tak szybko stłumi z(t), że PID ledwo zauważy zmianę y(t). Główną robotę tłumienia zakłócenia z(t) zrobi regulator podrzędny P a nadrzędny PID tylko ją dokończy.
Sprawdźmy to.

Rys. 30-25
Wyjście to czerwone y(t). Porównaj z odpowiedzią klasycznego układu zamkniętego–>Rys. 29-11 z rozdz. 29. Tłumienie zakłócenia z(t) super-tak jakby go nie było, ale odpowiedź na skok x(t) szkoda gadać. Łatwo to wytłumaczyć. Po prostu nastawy regulatora Kp=10 Ti=7 sek Td=2 sek zostały dobrane dla układu z Rys. 32-11 z rozdz. 32. A jak już pisałem we wstępie, bezwładność obiektu z Rys. 30-24 jest mniejsza, bo prawie znikła bezwładność zbiornika nr1 objętego pętlą wewnętrzną. Wniosek—> będą inne nastawy optymalne. Sprawdźmy.
Rozdz. 30.6.3 Układ Kaskadowy z jednym zakłóceniem i z bardziej optymalnymi nastawami
Nastawy regulatora PID tj Kp=10 Ti=5 sek i Td=0.55 sek dobrałem metodą prób i błędów. Chociaż mogą być nie do końca optymalne ,to powinna być wyraźna poprawa przebiegów czasowych.

Rys. 30-26
Przypominam, że wyjście to y(t)! Szok. A jak porównasz z odpowiedzią klasycznego układu zamkniętego Rys. 29-11 z rozdz.29, to megaszok! Jeszcze jedno. Spójrz np. na Rys. 30-25, gdzie w stanie ustalonym było s(t)=y(t)–> sygnał sterujący na wejściu obiektu s(t) zrównał się z sygnałem wyjściowym y(t). Przyzwyczailiśmy się, że „tak jest zawsze”. A na Rys. 30-36b tak nie jest(tu zamiast s(t) jest sPID(t)). Jak to wytłumaczyć? Sprawa jest prosta. Generalnie zawsze tak jest, że w stanie ustalonym jest s(t)=k*y(t), gdzie k jest wzmocnieniem statycznym obiektu z regulatorem. Przypominam, że stan ustalony to inaczej stan równowagi, który znalazł regulator. Gdy s(t) jest za duże, to regulator zmniejszy y(t) i vice versa. Do tej pory przy zwykłym sprzężeniu zwrotnym, przeważnie było k=1 i wtedy zawsze jest s(t)=y(t)?
A jak jest w regulacji kaskadowej na Rys. 30-24? Czy wzmocnienie obiektu między sygnałami sPID(t) a y(t)=TC3 jest równe k=1?
Nie! bo wewnętrzna pętla wokół zbiornika nr 1 zamykająca się przez regulator P, spowodowała, że Kz=0.909. Takie wzmocnienie „widzi” regulator nadrzędny PID.
A to oznacza, że w stanie ustalonym y(t)=0.909*sPID(t) czyli sPID(t)=1.1y(t). Potwierdza to Rys. 30-26

Rozdz. 30.6.4 Układ kaskadowy z dwoma zakłóceniami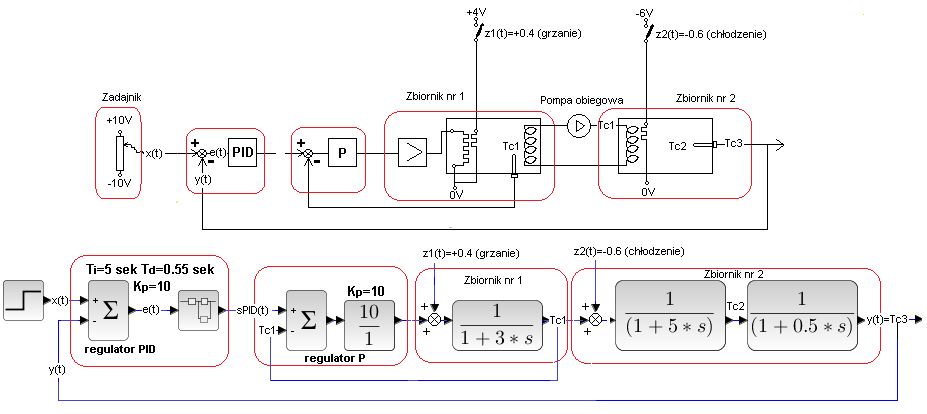

Rys. 30-27
Zakłócenie pierwsze z1(t)=+0.4 jest dodatkowym grzaniem wchodzącym na pętlę wewnętrzną. Czyli dokładnie tym samym co z(t)=+0.4 w poprzednich doświadczeniach. Dlatego spodziewamy się, że też będzie bardzo silnie stłumione.
Zakłócenie z2(t)=-0.6 jest chłodzeniem (minus na Peltierze!) wężownicy wejściowej do zbiornika 2. Jest objętym zwykłym sprzężeniem zwrotnym. Zakłócenie powinno też być całkowicie stłumione, choć nie tak szybko jak z1(t)

Rys. 30-28
Do 55 sek, czyli do pojawienia się z2(t), odpowiedź jest z oczywistych powodów identyczna z Rys. 30-26. Tłumienie zakłócenia z1(t) jest tak silne (czyli dobre!), że nie widać wpływu na sygnał wyjściowy y(t). Chociaż jest ale oscyloskop tego nie pokazuje.
W 55 sek wystąpiło zakłócenie z2(t)=-0.6 -chłodzenie przy wężownicy zbiornika 2. Regulator PID zareagował prawidłowo zwiększając moc grzałki zbiornika 1. Tu już widać wpływ zakłócenia z2(t), chociaż też zostało całkowicie stłumione. Czy regulator podrzędny P miał jakiś (pozytywny!) wpływ na tłumienie zakłócenia z2(t). Chyba tak. Przecież sprzężenie zwrotne wewnętrzne obejmujące zbiornik 1 tak jakby zmniejszyło jego bezwładność. Teraz prawie cała bezwładność dwóch zbiorników jest tylko w zbiorniku 2. A obiekty o mniejszych bezwładnościach są łatwiejsze do sterowania.

Rozdz. 30.7 Układ regulacji stosunku
Rozdz. 30.7.1 Wstęp
Sygnał wyjściowy y(t) zwykłego Układu Regulacji stara się śledzić sygnał wejściowy tak, żeby w stanie ustalonym było y(t)=x(t).
Układ Regulacji Stosunku wykonuje podobną robotę, tylko zgodnie ze wzorem y(t)=k*x(t).
Można go stosować np. w Mieszalni Farb–>Rozdz. 30.7.2, gdzie nowa farba powstanie ze zmieszania dwóch różnych. Wiadomo że kolor zależy od stosunku ich zmieszania. Wystarczy więc napełnić zbiornik mieszalni 2 przepływami dwóch farb np. czerwonej i zielonej, których przepływy są związane zależnością czerwony=k*zielony.
Inne zastosowanie to Kocioł Parowy–>Rozdz. 30.7.3. Wiadomo, że optymalne spalanie zależy od odpowiedniego stosunku gazu i powietrza. Jest źle gdy gazu jest za dużo. Wtedy nie dość, że nie wszystko się spali–>niska sprawność, to następuje zanieczyszczenie środowiska. A gdy gazu jest za mało? Co prawda wszystko się spali, ale nadmiar powietrza niepotrzebnie chłodzi kocioł i podgrzewa atmosferę zmniejszając sprawność energetyczną kotła. Należy więc zapewnić optymalny stosunek przepływów gazu i powietrza.
Rozdz. 30.7.2 Mieszalnia farb
Jest dobrym przykładem zastosowania Układu Regulacji Stosunku. Odpowiedni kolor to odpowiednia mieszanka trzech kolorów, tu dla uproszczenia tylko dwóch czerwonego i zielonego. Zależy nam na kolorze w którym zielony/czerwony=1/3 . Wystarczy więc napełnić zbiornik 2 przepływami z rurociągów- zielonego i czerwonego dla których stosunek przepływów to K=Fz/ Fcz=1/3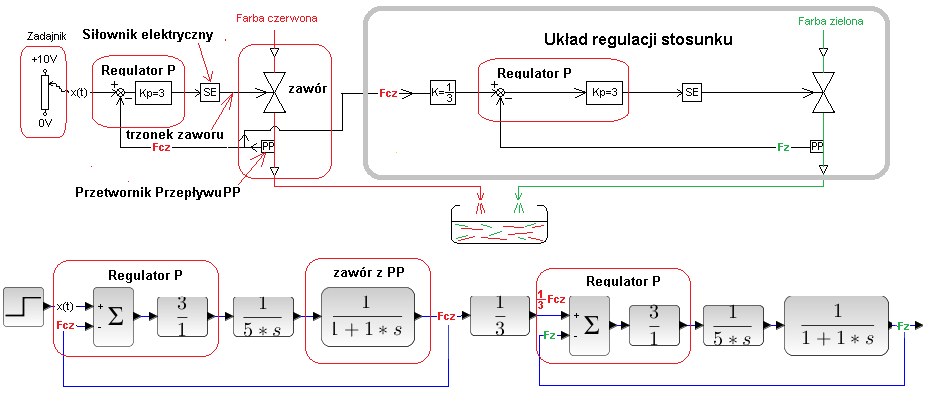

Rys. 30-29
Schemat technologiczny i schemat sterowania mieszalni
Teraz będzie coś o zaworach. Możesz opuścić jak znasz temat.
Układ Regulacji Stosunku najczęściej związany jest z przepływami. Przepływy na rurociągach sterowane są zaworami. Dlatego na początek absolutne minimum wiedzy. Każdy ma to w domu. Zawór zamknięty to brak przepływu, otwarty to przepływ maksymalny ograniczony tylko ciśnieniem w sieci, oporem hydraulicznym orurowania i oporem samego zaworu w pełni otwartego. Kręcąc kranem ustawiam przepływ pośredni, czyli mam możliwość sterowania.
Najważniejszą cechą każdego zaworu jest tzw. Kv. Dalej nie wchodzę w szczegóły. Powiem tylko, że mały kranik w domu to małe Kv, a duży zawór na rurociągu „Przyjaźń” to duże Kv.
Druga cecha to jego charakterystyka, czyli funkcja pomiędzy przesunięciem trzonka zaworu ( w domu to kąt obrotu kranika) a wywołanym przepływem F. Wydawałoby się, że wraz z odkręcaniem zaworu „dziurka”, czyli powierzchnia przez która płynie ciecz, powinna zwiększać się proporcjonalnie od 0 (zamknięty) do MAX (otwarty). Po to by przepływ też się zwiększał w sposób liniowy, co jest najbardziej pożądane w sterowaniu. A tu gucio.
Na początku powierzchnia zwiększa się powoli, a potem coraz szybciej. Coś na kształt funkcji wykładniczej. Jest to tzw. charakterystyka stałoprocentowa. Okazuje się, że właśnie taka nieliniowość zapewni ( w przybliżeniu) charakterystykę liniową zaworu, gdy wejściem jest przesunięcie trzonu zaworu (i grzybka) a wyjściem przepływ. Jak to wytłumaczyć?
Na początku jest mała „dziurka”, ale ciecz ma straszną ochotę przez nią płynąć, bo jest duży spadek ciśnienia miedzy dwoma stronami „dziurki”. Czyli jest większy przepływ niż wynikałoby to z małej powierzchni „dziurki”. Potem powierzchnia rośnie, ale chęć do przepływu maleje bo zmniejsza się spadek ciśnienia. W sumie wzrost powierzchni i spadek ciśnienia działają sobie na przekór i charakterystyka staje się bardziej liniowa.
Z powyższego wynika że dobierając zawór musisz dobrać:
a-takie Kv żeby dla x(t)=1 (+10V na potencjometrze) zawór był całkowicie otwarty–> maksymalny przepływ
b-zawór z charakterystyką stałoprocentową
ad.a
-Gdy za duży, to otworzy się tylko np. do 10% dając przepływ maksymalny ograniczony oporem zewnętrznego orurowania-szkoda dużego zaworu skoro można dać mniejszy czyli tańszy.
-Gdy za mały to otworzy prawie od razu na 100%, potem działa jako stały dławik, chociaż ciśnienie sieci i orurowanie mogło by dać większy przepływ.
ad.b-zapewnia pożądaną w automatyce liniowość
Jak działa mieszalnik?
Zadajnikiem – potencjometrem 0…+10V zadajemy maksymalny przepływ Fcz farby czerwonej, który mierzony jest przetwornikiem przepływu PP. Maksymalnemu przepływowi też odpowiada +10V na wyjściu przetwornika PP.
Regulator P porównuje wartość zadaną x(t) z aktualnym przepływem i wypracowuje odpowiedni sygnał sterujący na siłownik elektryczny SE. Sygnał ten przesuwa trzonek zaworu z prędkością proporcjonalną do napięcia z regulatora . Napięcie dodatnie otwiera zawór, ujemne zamyka a zerowe unieruchamia.
Jest to więc typowy człon całkujący o transmitancji 1/5s. Liczba 5 w mianowniku oznacza, że przy +10V,ale bez sprzężenia zwrotnego, zawór otworzy się na maxa w ciągu 5 sek*.  Zawór z przetwornikiem PP jest członem inercyjnym o stałej czasowej T=1 sek. Rurociąg z czerwoną farbą +automatyka tworzą układ regulacji I – czyli całkujący. Regulację I omówiliśmy dokładnie w rozdziale 28.
Podobnie działa część dotycząca farby zielonej. Tu z kolei wartością zadaną jest przepływ 1/3*Fcz. Spodziewamy się, że w stanie ustalonym przepływ Fz będzie 3 razy mniejszy od Fcz. Sprawdźmy.
* symbol s w transmitancji  1/5s to nie sekunda, ale liczba zespolona s, jak to w transmitancjach bywa.
Są to 2 regulacje typu I które dobrze znamy. Dlatego zbadamy tylko przebiegi x(t), Fcz i Fz.

Rys. 30-30
Cel Regulacji Stosunku został osiągnięty. Przepływ zielony Fz w stanie ustalonym to jedna trzecia czerwonego Fcz.
Rozdz. 30.7.3 Kocioł parowy
Jest mniej trywialnym przykładem Regulacji stosunku niż Mieszalnia farb.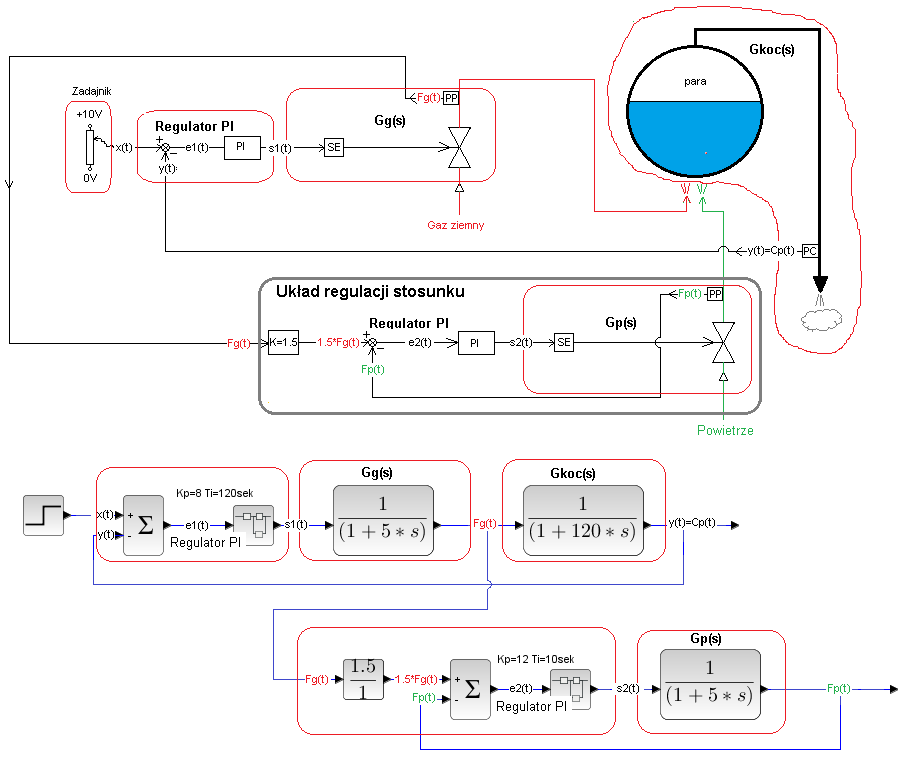

Rys. 30-31
Schemat technologiczny i blokowy typowego kotła parowego.
Jest to walczak wypełniony wodą i podgrzewany gazem ziemnym. Zasila parą różne urządzenia nie pokazane na schemacie. Automatyka stara się utrzymać stałe ciśnienie pary na wyjściu kotła cp(t) niezależnie od zakłóceń, którym może być np. włączenie dodatkowego odbiornika pary.
Gaz potrzebuje powietrza, ściślej tlenu. Spalanie optymalne zapewnione przy pewnym określonym stosunku przepływu powietrza do przepływu gazu. Gdy jest on za mały, to nie cały gaz zostanie spalony–> niższa sprawność i zanieczyszczenie środowiska.
Gdy za duży to niespalone powietrze niepotrzebnie chłodzi spaliny–> niższa sprawność.
Kotły to nie moja branża, ale k=10 jest podobno optymalne. Żeby wykresy gazu i powietrza mniej się różniły od siebie, to ze względów dydaktycznych założymy, że k=1.5.
Spójrzmy teraz okiem automatyka na schemat. Wyróżnimy w nim następujące bloki dynamiczne.
Kocioł parowy Gkoc(s)
Wejście – przepływ gazu Fg(t) i k=1.5 razy większy przepływ powietrza Fp(t)*
Wyjście -ciśnienie Cp(t) na rurociągu. Ściślej będzie to napięcie, gdzie 0…10V to 0…10 MPa.
Fizyka jest tu bardzo uproszczona. Zakładamy, że jakimś cudem utrzymuje się stały poziom wody niezależnie od wypływu pary. Zwykle robi to bardzo precyzyjny i szybki układ regulacji poziomu. Zapewnia on wahania mniejsze od 1 cm! A para cały czas zasuwa!
Kłania się tu Regulacja kaskadowa. Można też mierząc dodatkowo dopływ wody do walczaka i wypływ pary dokładnie obliczyć zakłócenie wpływające na poziom. Czyli Układ zamknięty z kompensacją.
Były to tylko uwagi na marginesie. Pozostajemy więc dalej przy cudzie stałego poziomu. Wzrost dopływu gazu Fg(t) i Fp(t) zwiększa temperaturę, a co za tym idzie ciśnienie Cp(t) pary. Oczywiście nie natychmiast, ale tak jak to robi człon inercyjny o stałej czasowej T=120 sek, objęty ujemnym sprzężeniem zwrotnym.
*Przepływ Fp(t) występuje tylko na górnym rysunku przy walczaku. Nie ma go natomiast na dolnym rysunku jako wejście do Gkoc(s). I słusznie, ponieważ ciśnienie pary Cp(t) zależy tylko od przepływu Fp(t), przy założeniu, że Fp(t)=k*Fg(t).
Blok sterowania gazem Gg(s)
Wejście – sygnał sterujący s1(t) z regulatora PI
Wyjście – przepływ gazu Fg(t)
SE-Siłownik Elektryczny- W odróżnieniu od siłownika SE w mieszalni, jest członem proporcjonalnym a nie całkującym. Ma on więc (nie pokazane na schemacie) wewnętrzne sprzężenie zwrotne od położenia trzonka . Znowu kłania się Regulacja kaskadowa –>będą lepsze przebiegi czasowe.
PP – przetwornik przepływu zamienia sygnał przpływu Fg(t) na 0…10V.
Zawór – Przesunięcie trzonka zamienia na zwiększenie powierzchni przepływu, czyli na zmianę przepływu. Projektant dobrał odpowiednią wielkość zaworu–>Kv i charakterystykę stałoprocentową w celu uzyskania liniowości. Zakładamy, że Gg(s) jest członem inercyjnym o stałej czasowej T=5 sek.
Regulator ciśnienia PI
Cały czas porównuje ciśnienie Cp(t) z wartością zadaną x(t).
Gdy Cp(t) wzrośnie to uchyb e1(t) zmaleje–>zmniejszy się Fg(t), spadnie temperatura wody iCp(t).
Gdy Cp(t) zmaleje to uchyb e1(t) wzrośnie–>wzrośnie się Fg(t), wzrośnie temperatura wody i ciśnienie pary Cp(t).
W ten sposób regulator stara się utrzymać ciśnienie Cp(t) na stałym poziomie równym wartości zadanej x(t). Regulacja PI zapewni zerowy uchyb i nie najgorsze przebiegi czasowe.
Blok sterowania powietrzem Gp(s)
Wejście – sygnał sterujący s2(t) z regulatora PI
Wyjście – przepływ powietrza Fp(t)
Działanie i dynamika taka sama jak Gg(s) – Blok sterowania gazem
Regulator przepływu PI
Wartością zadaną jest k*Fg(t). Dlatego regulator śledzi przepływ powietrza zapewniając Fp(t)=k*Fg(t).
Sprawdźmy jak działa cały system.

Rys. 30-32
Cel regulacji stosunku został osiągnięty. W stanie ustalonym przepływ powietrza jest 1.5 razy większy od przepływu gazu. Podkreślam, że przepływy gazu Fg(t) i powietrza Fg(t) są tu tylko sygnałami pomocniczymi. Najważniejszym jest ciśnienie pary Cp(t).