Podstawy automatyki

Rozdz. 29 Analiza zakłóceń

Rozdz. 29.1 Wstęp
Automatyka ma 2 główne zadania:
1. Dojście sygnału wyjściowego y(t) do wartości zadanej x(t) przez człowieka – operatora procesu technologicznego.
Ideałem jest stan ustalony w którym x(t)=y(t). Powinna to być też „ładna” odpowiedź na skok jednostkowy x(t). Co to znaczy „ładna”, inaczej „optymalna”, to już inna sprawa.
Dla Jednego będzie to najkrótszy czas regulacji, nawet z oscylacjami.
Dla Drugiego też najkrótszy czas, ale bez oscylacji.
Trzeci dopuszcza już 10% oscylacji.
Ten Pierwszy, Drugi i Trzeci to Pan Technolog albo Pan Klient który daje Automatykowi zarobić. Większość doświadczeń w tym kursie to badanie odpowiedzi y(t) na skok jednostkowy x(t).
2. Zapewnienie tłumienia zakłóceń z(t).
One cały czas próbują zepchnąć sygnał wyjściowy y(t) z drogi cnoty, którą jest utrzymanie y(t) na poziomie wartości zadanej x(t). Z tym właśnie walczy regulator. Ideałem jest stan gdzie pomimo zakłóceń cały czas jest e(t)=0. Jest to możliwe tylko w teorii. W praktyce jest tak, że dopiero po pewnym czasie zakłócenie z(t) będzie całkowicie stłumione. Przekonałeś się o tym badając wpływ zakłóceń z(t) w regulacji typu I, PI i PID. Regulacja P i PD chociaż tłumi uchyb, to nie do końca. Ona go tylko zmniejsza np. do 2%, w porównaniu do układu bez regulacji.
Uwaga
Optymalna odpowiedź na skok x(t) z reguły nie zapewnia optymalnej odpowiedzi na zaklócenie z(t) i vice versa.

Rozdz. 29.2 Działanie wartości zadanej x(t) i zakłócenia z(t) na sygnał wyjściowy y(t)
– Działanie x(t) na y(t) zawarte jest w transmitancji układu zamkniętego Gz(s)=y(s)/x(s)
– Działanie z(t) na y(t) zawarte jest w transmitancji zakłóceniowej Gzakl(s)=y(s)/z(s)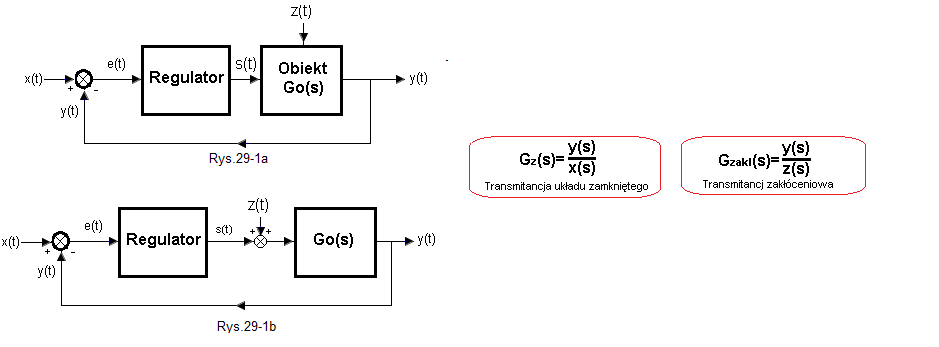

Rys. 29-1
Rys. 29-1a używany jest, gdy niezbyt dokładnie znamy wpływ zakłóceń z(t) na obiekt. Czujemy, że regulator stara się stłumić zakłócenie, ale jak to robi to już jego sprawa. W tej postaci nie da się sprawdzić jak y(t) odpowie na na skok zakłócenia z(t). Dlatego dokładniejszym przybliżeniem będzie Rys. 29-1b z konkretną sytuacją. Tu zakłócenie z(t) dodaje się bezpośrednio do sygnału sterującego z regulatora s(t). Na przykład, gdy obiekt jest piecem i s(t) jest mocą podawaną z regulatora na grzałkę . Zakłóceniem dodatnim z(t) będzie wtedy moc podawana na osobną grzałkę położoną blisko grzałki sterującej.
Wprowadźmy trochę więcej matematyki. Tu R(s) jest transmitancją , którą może być regulator typu PID.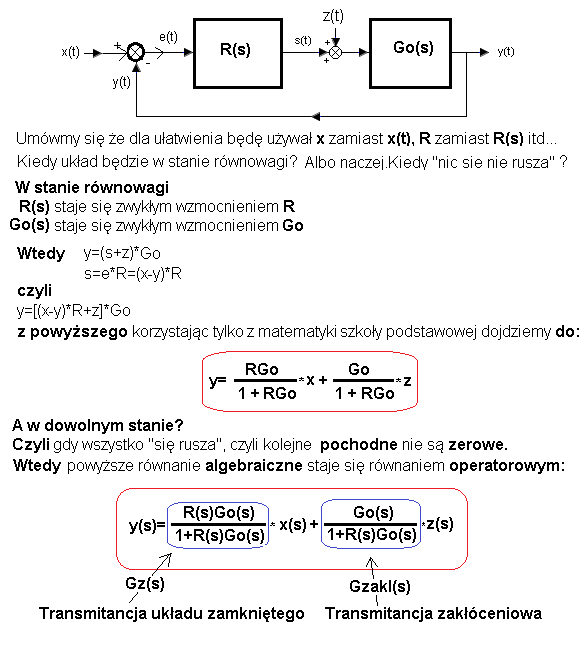

Rys. 29-2
Zwróć uwagę na to, że transmitancja układu zamkniętego Gz(s) jest taka sama jak ” w najważniejszym wzorze”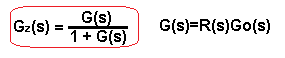

Rys. 29-3
Za to w liczniku transmitancji zakłóceniowej Gzakl(s) nie występuje R(s). Tak więc Gzakl(s) ma trochę mniej bezwładności niż Gz(s). Dlatego odpowiedź na zakłócenie z(t) jest przeważnie trochę szybsza niż na x(t)! Stąd też gdy dobieramy nastawy PID musimy się zdecydować.
Na czym bardziej nam zależy?
Na optymalnej odpowiedzi na x(t) czy na z(t)?
Jeżeli zmiany wartości zadanej występują często to stroimy regulator ze względu na wartość zadaną x(t), gdy rzadko to ze względu na z(t).
Częściej jednak kierujemy się strojeniem regulatora ze względu na wartość zadaną x(t), bo ta jest bardziej przewidywalna niż na zakłócenie z(t). Przypomina to metodę gościa, który szuka klucza pod latarnią tylko dlatego, że lepiej widać. Z drugiej strony różnice w strojeniu ze względu na x(t) albo z(t) rzadko są szokująco duże.
A gdy zakłócenie jest w “środku” obiektu Go(s), tak jak na Rys. 29-4a?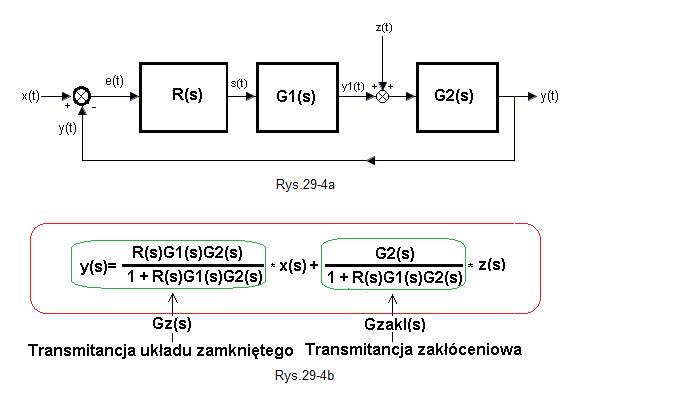

Rys. 29-4
Rys. 29-4a jest dokładniejszym przybliżeniem Rys. 29-1a, w którym z(t) pojawia w „środku” obiektu Go(s)=G1(s)*G2(s), tj. między transmitancjami G1(s) i G2(s).
Wzór z Rys. 29-4b wynika bezpośrednio z Rys. 29-2. Wystarczy tylko założyć że G1(s) wchodzi w skład transmitancji regulatora i wynosi R(s)*G1(s) a obiektem będzie G2(s). Ze wzoru na transmitancję zakłóceniową Gzakl(s) wynika, że im bliżej wyjścia obiektu jest zakłócenie z(t) tym wyraźniejszy będzie jego wpływ na y(t). Co oznacza „bliżej wyjścia”? To, że bezwładność G2(s) jest mniejsza w porównaniu do bezwładności G1(s). Inaczej transmitancja G2(s) staje się bliższa członu proporcjonalnemu G2(s)=1. Czyli zakłócenie z(t) będzie mniej „spłaszczone” przez G2(s). Przekonasz się o tym w dalszej części tego rozdziału.

Rozdz. 29.3 Dwustopniowy wymiennik ciepła
Rozdz. 29.3.1 Po co wchodzimy w technikę cieplną?
Dwustopniowy wymiennik ciepła jest dobrym przykładem dla:
– Analizy zakłóceń
– Różnych struktur układów regulacji które będą omówione w następnym rozdziale.
Rozdz. 29.3.2 Wymiennik ciepła w układzie otwartym
Zbadamy sam obiekt bez regulacji, czyli w układzie otwartym.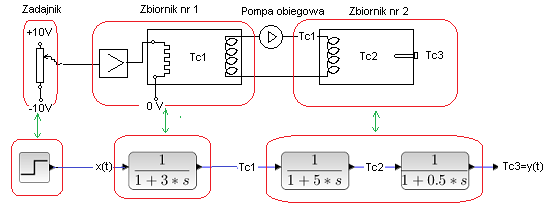

Rys. 29-5
Schemat ma służyć do poznania zasad automatyki a nie procesów cieplnych zachodzących w wymienniku. Dlatego dokonamy baaaardzo dużych uproszczeń.
1– Ciecz nie paruje ani nie zamarza. Czyli może osiągnąć temperaturę np. +1000ºC a nawet -1000ºC, co jest jeszcze bardziej absurdalne. Grzejący plus na grzałce to normalne, ale chłodzący minus? Jednak już od 19 wieku znany jest tzw. element Peltiera. Taka grzałko-chłodziarka ułatwia zrozumienie ujemnego sygnału sterującego sPID(t), który w pewnych bardzo krótkich momentach „chce” schłodzić ciecz do temp. np -1200 ºC!. Co to znaczy „chce”? To, że w tej chwili nie schłodzi do tej temperatury. Ale gdyby cały czas do grzałko-chłodnicy była podawana taka moc chłodząca (czyli ujemna), to po pewnym czasie ciecz osiągnęłaby -1200 ºC.
2– W zbiornikach cały czas pracują mieszadła ( nie ma ich na schemacie), czyli w każdym miejscu danego zbiornika jest taka sama chwilowa temperatura Tc1 lub Tc2. Chwilowe Tc1 może się różnić od chwilowego Tc2. Może ona rosnąć lub maleć w zależności od położenia suwaka zadajnika.
3– Ciepło przenoszone jest ze zbiornika nr 1 do zbiornika nr 2 poprzez wężownicę wyjściową zb. 1 i wejściową zb. nr 2. Transport ciepła ułatwia pompa obiegowa, podobnie jak pompa w budynku wymuszająca przepływ wody przez kaloryfery. Ciecz w wężownicy wejściowej zbiornika nr 2 ma temperaturę Tc1 czyli temperaturę cieczy w zbiorniku nr 1. Dlatego Tc1 jest sygnałem wejściowym do zbiornika nr 2. Analogicznie napięcie ze wzmacniacza na grzałkę- jest sygnałem wejściowym dla zbiornika nr 1. W stanie ustalonym będzie Tc1=Tc2=Tc3.
4-Moc na grzałce jest proporcjonalna do napięcia ze wzmacniacza, a nie do kwadratu napięcia. Jest to oczywiście sprzeczne z elektrotechniką, ale dzięki temu temperatura cieczy będzie proporcjonalna do napięcia z zadajnika i łatwiejsza będzie analiza przebiegów czasowych.
5– Jak na zadajniku będzie np. +10V odpowiadające temperaturze +100 ºC to po pewnym czasie w zb. nr 1 pojawi się Tc1=+100 ºC a potem w zb. nr 2 też będzie Tc2=+100 ºC. Ta temperatura „oblewająca” obudowę czujnika platynowego (drucika platynowego) podgrzeje ten drucik i przetwornik pokaże temperaturę Tc3=+100ºC w postaci napięcia +10V.
Zauważ, że w stanie ustalonym na wejściu jest +10V i na wyjściu też +10V. Czyli cały wymiennik ze wzmacniaczem mocy, wężownicami itd. możesz traktować jak wzmacniacz o wzmocnieniu K=1 i pewnej dynamice–> tu człon trójinercyjny. To bardzo ułatwia analizę!
Analogicznie:
+5V–>Tc1=Tc2=Tc3=+50ºC–>+5V
0V–>Tc1=Tc2=Tc3=0ºC–>0V
-5V–>Tc1=Tc2=Tc3=-50 ºC–>-5V
-10V–>Tc1=Tc2=Tc3=-100 ºC–>-10V
6– Zerowe warunki początkowe–> Tc1=Tc2=Tc3=0ºC
7 – Wzmacniacz mocy o wzmocnieniu napięciowym ku=1 zapewnia, że na grzałce jest napięcie x(t) niezależnie od obciążenia (albo oporu) grzałki.
Zbadamy wpływ miejsca zakłócenia na sygnał wyjściowy y(t). Okaże się, że im bliżej wyjścia obiektu jest zakłócenie z(t), tym wyraźniejszy jest jego wpływ. Zakłócenia będą wchodzić na trójinercyjny obiekt Go(s), którego przykładem jest wymiennik ciepła.
Suwak zadajnika z Rys. 29-5 zostanie teraz gwałtownie przesunięty z pozycji środkowej do górnej. W ten sposób skokowo zadasz temperaturę od x(t)=0ºC do x(t)=+100ºC. Odpowiada to modelowi i animacji na Rys. 29-6.

Rys.29-6
Skok 0ºC do +100ºC który odpowiada skokowi 0 do 1
Model wymiennika z poprzedniego rysunku. Nie ma w nim wzmacniacza mocy bo ku=1.
Biorąc pod uwagę niewielkie stałe czasowe, nasze zbiorniki są wielkości szklanek. Dlatego do sterowania grzałką powinien wystarczyć poczciwy wtórnik emiterowy. Tu część mocy jest tracona na tranzystorze. Dla większych wymienników stosuje się wzmacniacze impulsowe. Nie wnikajmy też za bardzo, czy są tak małe termometry Pt100 w obudowie. Załóżmy, że są takie mikrusy.
Wyraźnie widać trójinercyjność sygnału Tc3=y(t) oraz jak temperatura Tc1 wyprzedza Tc2, a ta Tc3. Dzięki małej stałej czasowej termometru Tc3 to prawie Tc2. Potwierdziły się nasze założenia że:
-temperatury chwilowe Tc1, Tc2 i Tc3 mogą być różne
-w stanie ustalonym wszystkie temperatury zrównały się->Tc1=Tc2=Tc3=100ºC
Rozdz. 29.3.3 Wymiennik w układzie zamkniętym
Klasyczny układ regulacji automatycznej bez zakłóceń.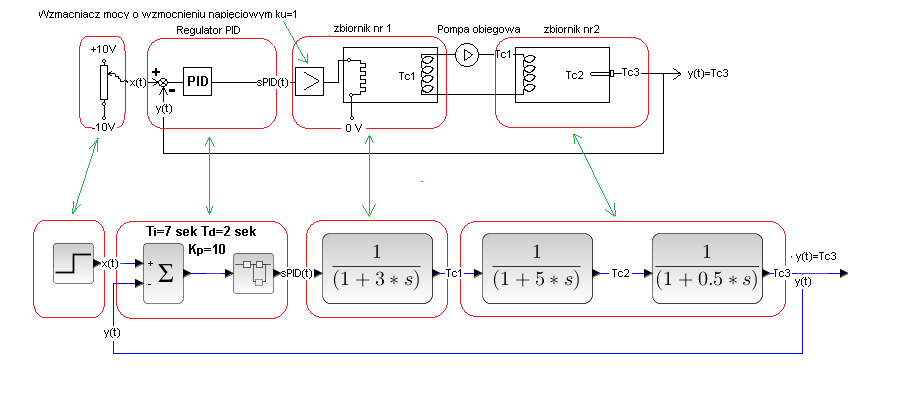

Rys. 29-7
Schemat technologiczny na górze i odpowiadający mu schemat blokowy na dole.
Wejściem do zbiornika nr 1 jest sygnał z regulatora PID a ściślej z jego wzmacniacza mocy zaś wyjściem jest temperatura Tc1 wężownicy wyjściowej, taka sama jak temperatura cieczy w zbiorniku. Jest to jednocześnie sygnał wejściowy do zbiornika nr 2 gdyż w jego wężownicy też jest temperatura Tc1.

Rys. 29-8
Jak się dobrze przyjrzysz to już wcześniej badałeś ten schemat–>Rozdz.27 Rys.27-29. Wtedy tylko nie kojarzyłeś go z 2 wymiennikami ciepła oraz z napięciowym wyjściem Tc3  0…+10V na termometrze Pt100. Właściwie to na jego przetworniku, który zmiany rezystancji drucika platynowego (stąd nazwa PT100) przetwarza na zmiany napięcia.
Uwaga ogólna
Tu jest dużo przebiegów czasów, od których można dostać oczopląsu. Abu ułatwić zadanie proponuję analizować “po kawałku”.
1. Najpierw najważniejsze tzn. wejście i wyjście  czyli x(t) i y(t).
2. Uchyb e(t)=x(t)-y(t)–>Sprawdź czy się zgadza dla każdego t.
3. Sygnał sterujący SPID(t). Czy też byś tak sterował ręcznie?
4. Kolejne “łagodniejące” sygnały Tc1, Tc2 i Tc3. Zauważ, że Tc3 już analizowałeś jako y(t)=Tc3.
Później też stosuj tę zasadę.

Rys. 29-9
Poprzedni przebieg tylko inna skala oscyloskopu, dlatego widzisz też to, co było „ucięte” na Rys. 29-8.
Zadajnik x(t) wymusza skokowo w 3 sek. +10V. Czyli „życzy” sobie ,żeby po pewnym czasie na termometrze też było +10V. Czyli y=Tc3=+100ºC. Pamiętamy, że temperatura początkowa cieczy w zbiornikach Tc1=Tc2=0ºC. W 3 sek ( w momencie skoku) uchyb e(t)=+100ºC. Składowa P regulatora PID wymusza wtedy sygnał sterujący odpowiadający mocy która w stanie ustalonym (gdyby się nie zmieniała) daje +1000ºC! (tu Tc1=10) Szok? To może być jeszcze większy. Przecież składowa D różniczkuje skok i daje =+200 . W sumie w momencie skoku regulator daje sygnał sPID(t)=210 co odpowiada temperaturze +21 000ºC. Więcej niż na słońcu! I tak mamy szczęście, że w regulatorze PID składowa różniczkująca D jest rzeczywista tzn. „spłaszczona” przez człon inercyjny. Gdyby to był idealny człon różniczkujący, to moc na grzałce odpowiadałaby wtedy przez chwilę niekończonej temperaturze! Bomba wodorowa to pikuś. A to wszystko dzieje się w zbiorniczku nr 1 mniejszym od szklanki.
Po co straszę czytelników? Po to by mieć świadomość, że do tej pory modelowaliśmy obiekty idealne. Tzn nie było żadnych ograniczeń. A w życiu a tym bardziej w elektronice one występują. Nasz wzmacniacz mocy- wtórnik emiterowy wchodzi w nasycenia wynikające z jego zasilania np. -15V…+15V. W systemach idealnych ujemne napięcie chłodzi temperaturą . W systemach rzeczywistych sygnał ujemny SPID(t) tylko wyłącza dopływ mocy do grzałki. Czyli temperatura Tc3 będzie spadać tylko do temperatury otoczenia. A poza tym nawet w systemach idealnych nie ma „bomb wodorowych”-potężnych energii. Co z tego że są przez bardzo krótkie chwile duże moce. Ale energia może być już normalna bo to jest moc*czas.
Przy okazji. Układy regulacji z elementem Peltiera stosuje się tylko w szczególnych przypadkach, gdy wymagane są bardzo szybkie zmiany temperatur.
Co z tego wynika? Przebiegi idealne dają przez bardzo krótkie okresy bardzo silne sygnały sterujące za regulatorem. Na początku skoku x(t) sygnał sterujący sPID(t)=210 co odpowiada temperaturze +21000ºC! Temperatura cieczy nie zdąży oczywiście osiągnąć tej wartości, ale za to bardzo szybko wzrasta. Sprzężenie zwrotne jeszcze szybciej zmniejsza ten sygnał, nawet przez chwilę chce schłodzić ciecz do =-1200ºC! Widać to na Rys. 29-9. Przebiegi rzeczywiste mają ograniczenia i dlatego będą wolniejsze. Poza tym raczej rzadko zmienia się wartość zadana x(t). Najczęściej regulator pracuje w trybie tłumienia zakłóceń z(t) a nie gdy zmienia się wartość zadana x(t). Zakłócenia z(t) są zwykle dużo mniejsze niż skoki x(t). Wtedy też sygnały sterujące sPID(t) mniej wchodzą w nasycenia i przebiegi będą bardziej zbliżone do idealnych. Więcej na ten temat dowiesz się w rozdziale 31.

Rozdz. 29.4 Regulacja temperatury wymiennika z zakłóceniami w różnych miejscach
Rozdz. 29.4.1 Wstęp
Z Rys. 29-4b wynika, że im bliżej wyjścia y(t) jest zakłócenie z(t) tym silniejszy będzie jego wpływ . Sprawdzimy to w naszym wymienniku.
Na układ regulacji z Rys. 29-7 wprowadzimy kolejno zakłócenie przed pierwszą, drugą albo trzecią inercją. Zakłóceniem będzie włożenie dodatkowej grzałki. Zobaczymy jak sobie regulator PID z tym poradzi. Na koniec wprowadzimy najbardziej złośliwe zakłócenie – bezpośrednio na wyjście termometru.
Rozdz. 29.4.2 Zakłócenie przed pierwszą inercją – dodatkowa grzałka przy grzałce zbiornika 1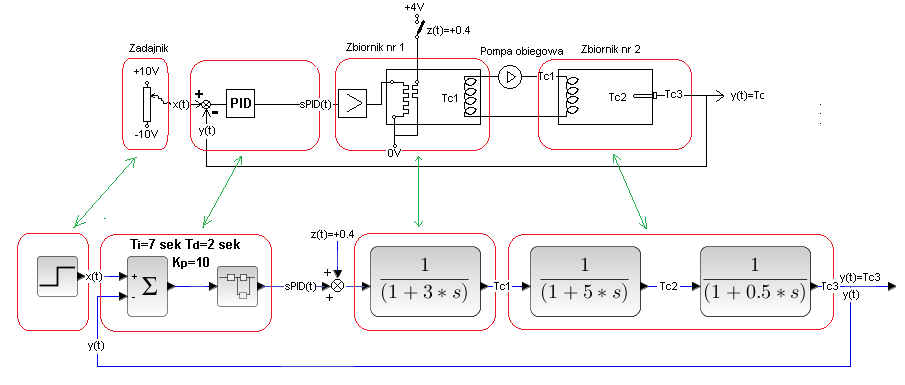

Rys. 29-10
Zakłóceniem będzie skok napięcia +4V (zwarcie styku) na dodatkowej grzałce tuż przy grzałce głównej w zbiorniku nr 1. Spowoduje to dodatkowe grzanie. Rezystancje grzałki sterowanej przez wzmacniacz i dodatkowej są jednakowe. Czyli takie samo napięcie na dwóch grzałkach powoduje taki sam wzrost temperatury otaczającej cieczy.

Rys. 29-11
W stanie ustalonym zakłócenie z(t) spowodowane 40% grzaniem zostało skompensowane przez PID spadkiem napięcia (chłodzeniem) 40%. W rezultacie temperatura y(t) ledwo drgnęła. Przypominam, że 1 na wykresie odpowiada temperaturze =+100ºC.
Rozdz. 29.4.3 Zakłócenie przed drugą inercją – dodatkowa grzałka przy wężownicy zbiornika 2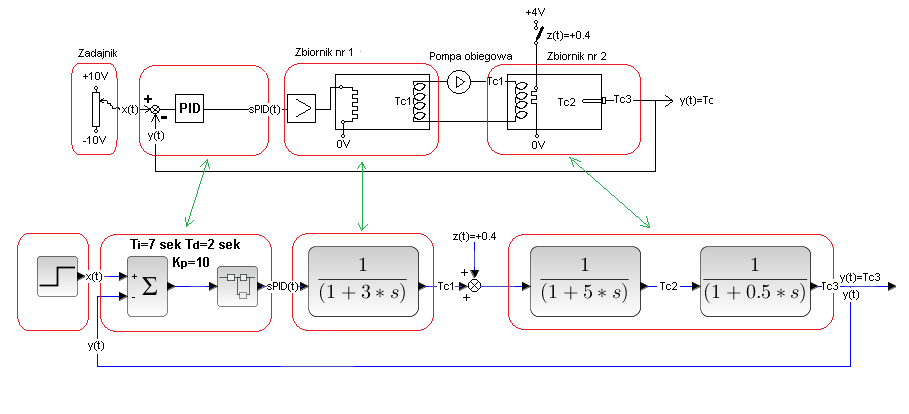

Rys.29-12

Rys. 29-13
Reakcja y(t) na skok x(t) jest identyczna jest poprzednio. Jest to oczywiste
Reakcja y(t) na zakłócenie z(t) jest bardziej gwałtowna i trwa krócej niż poprzednio. Silniejsza jest też reakcja PID-a, czyli niebieskiego sPID(t).
Rozdz. 29.4.4 Zakłócenie przed trzecią inercją – grzałka działa bezpośrednio na część termometru zbiornika nr 2
Przekonasz się, jak złośliwe potrafi być zakłócenie działające bezpośrednio na wyjście lub bardzo blisko wyjścia. Zakłóceniem z(t) jest skok napięcia na grzałce, która jest drucikiem oporowym nawiniętym obudowę termometru Pt100.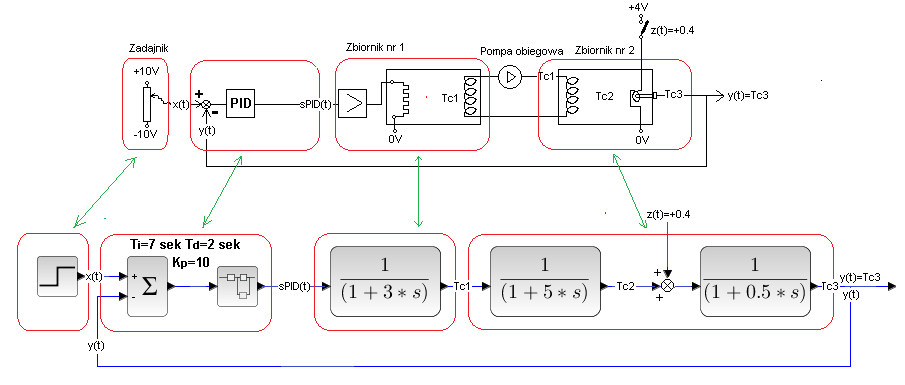

Rys. 29-14
Klika zwojów zwojów drutu oporowego grzałki „okrąża” kawałek obudowy termometru.
Dlatego na termometr wpływają:
– temperatura cieczy Tc2 w zbiorniku nr 2
– grzałka „okrążająca” kawałek termometru
Zakładamy też, że parametry „grzejące termometr” od grzałki są takie same jak parametry „grzejące termometr” od cieczy opływającej część termometru nieobjętą grzałką.
Zakłóceniem będzie skok napięcia z(t)=+4V na grzałce.

Rys. 29-15
W stanie ustalonym zakłócenie z(t) spowodowane 40% dodatkowym grzaniem termometru zostało skompensowane przez PID 40% spadkiem mocy. Efekt zakłócenia jest jeszcze silniejszy niż poprzednio, bo zakłócenie ma bliżej do wejścia PID-u. Dlatego regulator reaguje energiczniej na z(t). Jest to widoczne na niebieskim sPID(t). Cieszymy się że jest cacy. Tc3 wróciło do poprzedniej wartości. Ale co to jest Tc3? Jest to napięcie na termometrze. A dla nas ważna jest temperatura cieczy Tc2 w drugim zbiorniku, a nie jakieś napięcie. To zbadajmy przebieg Tc2.

Rys. 29-16
W odróżnieniu od poprzedniego schematu możemy obserwować także temperaturę cieczy Tc2 w zbiorniku nr 2. Prawdziwa temperatura cieczy to Tc2. Uwaga- Tc2 jest żółte a ten kolor jest ledwo widoczny na białym tle! Okazuje się że w stanie ustalonym ciecz w zbiorniku nr 2 ma Tc2=60ºC! Po prostu PID jak każdy porządny regulator stara się zrównać sygnał wyjściowy y(t)=Tc3 z wartością zadaną x(t) odpowiadającą temperaturze 100ºC. I to mu się udaje w 100%, co widać na czerwonym y(t). Tyle tylko, że wskazania termometru są sfałszowane przez dodatkowe podgrzewanie obudowy termometru. Regulator „myśli”, że temperatura cieczy to Tc3=100ºC. A tymczasem wstanie ustalonym Tc3=Tc2+40ºC=100ºC. Czyli Tc2=60ºC co widać na załączonym obrazku.
Pamiętacie wypadki górnicze na Śląsku. Specjalnie nadmuchiwano świeżym powietrzem czujnik metanu . Stężenie metanu przy samym czujniku było cacy i maszyny z iskrzącymi silnikami elektrycznymi nie były wyłączane. Szła premia za wydobycie i 100 razy rosyjska ruletka się udała ale za 101 razem… Wynik pomiaru został sfałszowany, podobnie jak w naszym przykładzie z podgrzewaniem obudowy termometru.
Rozdz. 29.4.5 Najbardziej złośliwe zakłócenie- bezpośrednio na wyjście! (za termometrem)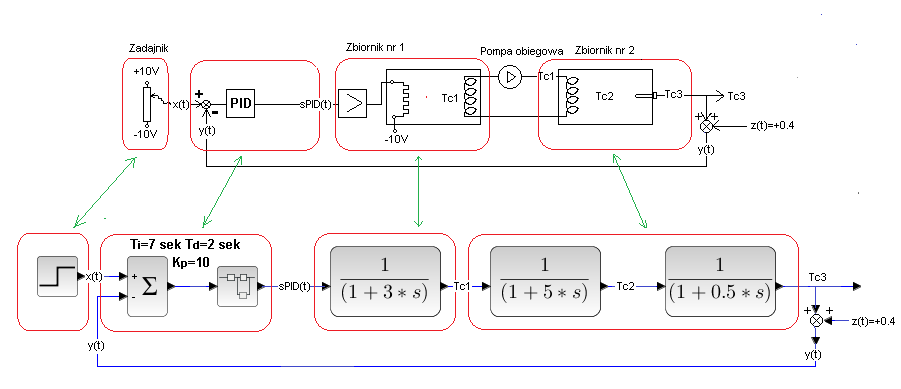

Rys. 29-17
Jest to podobne zakłócenie do poprzedniego, ale bardziej jadowite. Tu nie podgrzewamy termometru, ale dodajemy napięcie do wyjścia termometru! Czyli oszustwo na całego. Do regulatora dochodzi „fałszywa” zawyżona temperatura y(t)=Tc3 + z(t). Regulator w stanie ustalonym wykona swoją robotę tzn. zrówna  x(t)=y(t) ale prawdziwa temperatura cieczy będzie równa Tc3(t)=y(t)-z(t)=100ºC–40ºC=60ºC.

Rys. 29-18
Gdy w 25 sek pojawi się z(t)=+0.4 to regulator myśli, że w zbiorniku jest teraz y(t)=+140ºC (chociaż Tc3=+100ºC). Dlatego, usiłując sprowadzić uchyb e(t) do zera, tak zmniejszy grzanie czyli sPID(t), aby y(t) znowu było 100ºC. I to mu się uda tyle tylko, że wtedy stanie ustalonym będzie Tc3=+60ºC.
Porównaj reakcję y(t) na zakłócenie z Rys. 29-16. Tu skok y(t) do 1.4 (czyli do+140ºC). Dlaczego. Bo tu dodaje się napięcie do termometru, a na Rys. 29-16 termometr był podgrzewany.

Rozdz. 29.5 Najważniejsze wnioski dotyczące zakłóceń
1. Im bliżej wyjścia tym wyraźniejszy wpływ zakłócenia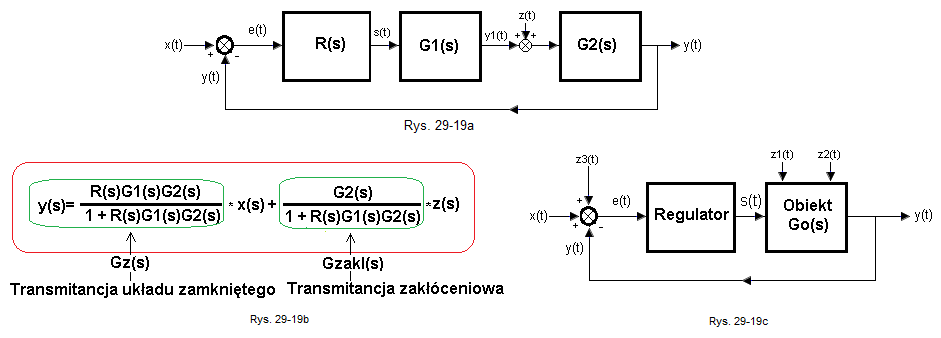

Rys. 29-19
Wg Rys. 29-19 zakłócenie z2(t), które jest „bliższe” wyjścia y(t), będzie wywoływało silniejszy sygnał sterujący s(t) i wyraźniejsze zmiany y(t), niż zakłócenie z1(t).
Uzasadnieniem jest wzór z Rys.29-19b przedstawiający zależność między zakłóceniem z(t) i wejściem x(t) a wyjściem y(t). Im bardziej z(t) przesuwa się w prawo do wyjścia y(t), tym bardziej zmniejsza się bezwładność G2(s). A co to oznacza? Zmniejsza się „bezwładność” transmitancji zakłóceniowej Gzakl(s) bo jej licznik dąży do 1. Czyli odpowiedź z(t) jest wyraźniejsza i krótsza. Potwierdzają to przebiegi y(t) na rys. 29-11, 29-13, 29-15, 29-16  i 29-18 na których z(t) „przesuwa się” od lewej do prawej.
2. Zakłócenia bezpośrednio na wyjście – najbardziej perfidne
Przykładem jest czujnik w rozdz. 29.4.4 i 29.4.5. Daje on regulatorowi fałszywą informację, na którą regulator reaguje, tak jakby była prawdziwa. Tak jest nie tylko w automatyce. Najbardziej złośliwe są zakłócenia czyli sfałszowane sygnały, które bezpośrednio wpływają na proces decyzyjny. Czytaliście „Igłę” Kena Folleta? Tu brytyjski wywiad podsunął najlepszemu agentowi Hitlera (czyli czujnikowi Hitlera) informację, że inwazja w 1944 r będzie tu, a nie tam. No i Adolf zatrzymał na kilka dni swoje najlepsze dywizje.
Bezpośrednie zakłócenie na wyjście, jest jednocześnie zakłóceniem na wejście ( ze zmienionym znakiem). Inny przykład to z(t) na Rys. 29-18. Regulator „myśli”, że wartością zadaną jest x(t)+z(t) i do niej stara się  doregulować wartość y(t). To tak jakby kapitan Kloss (młodzi czytelnicy znają go?) przebrał się za Hitlera i wydawał rozkazy. Dlatego konstruktorzy starają się maksymalnie zabezpieczyć regulator go przed zakłóceniami. A to jest łatwiejsze niż zabezpieczenie całego toru sygnałowego.